夏普比率 0.6，该抛弃吗？

夏普比率 0.6，该抛弃吗？

我们做一个实验来说明这个问题。这个实验从一些关键性假设开始。我们有 20 个交易信号，这些交易信号的年复合收益率为 8%，年化夏普比率为 0.6。 这个策略的信号并不高产。 这些交易信号每天都发出来。实验中策略持续期为十年 （每日交易）， 但是之后我们会展示观测样本减少时统计数据发生的变化。实验一共重复 500 次，并得到相关统计数据的分布，如年复合收益率和年化夏普比率。

• 交易中一个重要的输入变量是信号之间的相关性。我们按照相关系数从 0 到 0.9 进行一系列实验。实验不考虑交易成本（因为我们只对相对业绩感兴趣），而且根据相关性每日再平衡的年化组合收益率的分布基本一样。显然，不考虑策略相关性的前提下，策略多于一种不会提高年化收益率。

  

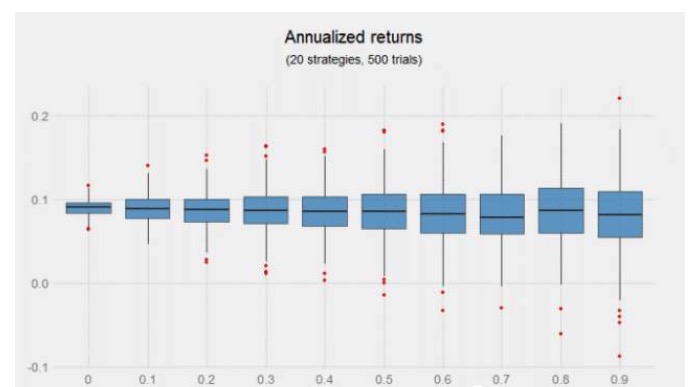
  将相关性低的信号组合在一起不提高收益，但是上图暗示增加策略可能带来的好处，尤其是在这些策略不相关的情况下。图中左半边，即相关系数从 0 到 0.4 ，分布更窄而且五百次实验的收益均为正。

  当使用夏普比率来衡量风险调整收益后，实验结果更加清晰。将 20 个年化夏普比率为 0.6、彼此相关系数为0的策略构造成一个组合，该组合的年化夏普比率为 3，而将 20 个年化夏普比率为 0.6、彼此平均相关系数为 0.9 的策略构造成一个组合，该组合的年化夏普比率为 0.64，前者比后者的收益高 370%。

  

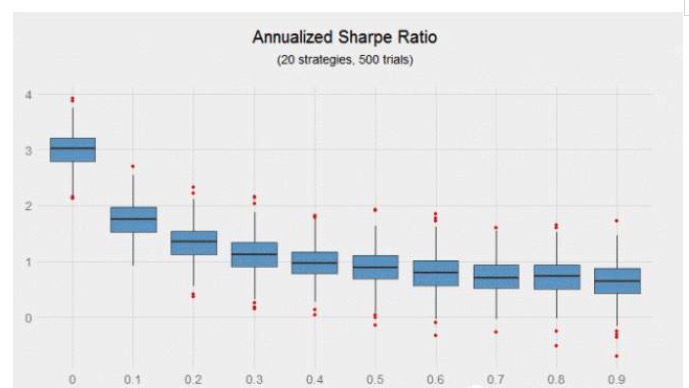
  上图中值得注意的是随着策略的相关性增强，夏普比率的下降速度很快。相关系数从 0 增加到 0.2，夏普比率就下降了 56%。

  即便有很高的夏普比率，这个组合策略有近 50000 次交易信号，相关性为零的组合的夏普比率的方差依然让人吃惊。一个幸运的投资者可能获得 3.5 的夏普比率（可能让一个人成为亿万富翁）而持有相同组合的运气不好的投资者却只获得 2.5 的夏普比率。即使是高夏普比率的组合，运气也扮演着一个重要的角色。

  显然，观测样本越多，边界越清晰。如果一个投资者只有一年的观测样本而非十年的，会发生什么呢？下图表明随着相关性增强，夏普比率的方差呈现指数式增长）尽管有 5000 个交易，大多数投资组合离不开随机的运气成分。显然这就是数据驱动型的对冲基金偏爱高频交易的原因，高频交易能更快地验证信号，实现其夏普比率的平均值。

  

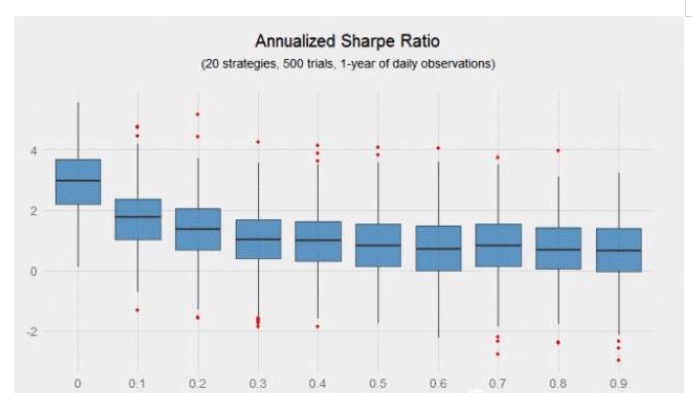
  如果我们模拟 10000 个上述的单个策略，有多大比例的 p 检验值低于 5%？答案是接近 48%，这可能会导致大多数研究人员放弃这样的日常策略（即年化夏普比率为 0.6 的策略）。但是，如果信号间的相关性足够低，将这些弱信号组合在一起能够产生奇迹，组合的回报流会变得非常显著。所有零相关的投资组合的 p 值小于 5%。

  

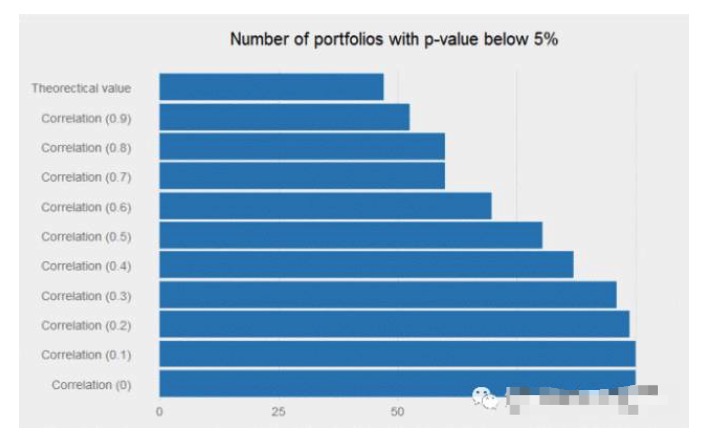
  一个年化夏普比率为 0.6 的策略可能因为在交易中不具有任何吸引力而被研究人员舍弃。但是如果它与现有的信号之间有正确（即低）的相关性，那么它可以很好地增加组合的价值。

  本文没有开辟新领域，因为分散投资的好处是投资界众所周知的。但它确实提醒你未必要放弃年化夏普比率为 0.6 的策略，或许你可以把它添加到你现有的策略组合中，从而降低组合的流动性和允许使用更多的杠杆来提高总收益。

转载自 私募工场