统计基础篇之七：骗人的“平均数”

统计基础篇之七：骗人的“平均数”

关于均值、中位数、众数，很多人概念上有些模糊。

• 有一个广为流传的笑话，这里转帖一下，也许会对大家理解上有所帮助。

  M：吉斯莫先生有一个小工厂，生产超级小玩意儿。

  M：管理人员由吉斯莫先生、他的弟弟、六个亲戚组成。工作人员由5个领工和10个工人组成。工厂经营得很顺利，现在需要一个新工人。

  M：现在吉斯莫先生正在接见萨姆，谈工作问题。

  吉斯莫：我们这里报酬不错。平均薪金是每周300元。你在学徒期间每周得75元，不过很快就可以加工资。

  M：萨姆工作了几天之后，要求见厂长。

  萨姆；你欺骗我！我已经找其他工人核对过了，没有一个人的工资超过每周100元。平均工资怎么可能是一周300元呢？

  吉斯莫：啊，萨姆，不要激动。平均工资是300元。我要向你证明这一点。

  吉斯莫：这是我每周付出的酬金。我得2400元，我弟弟得1000元，我的六个亲戚每人得250元，五个领工每人得200元，10个工人每人100元。总共是每周6900元，付给23个人，对吧？

  萨姆：对，对，对！你是对的，平均工资是每周300元。可你还是蒙骗了我。

  吉斯莫；我不同意！你实在是不明白。我已经把工资列了个表，并告诉了你，工资的中位数是200元，可这不是平均工资，而是中等工资。

  萨姆：每周100元又是怎么回事呢？

  吉斯莫：那称为众数，是大多数人挣的工资。

  吉斯莫：老弟，你的问题是出在你不懂平均数、中位数和众数之间的区别。

  萨姆：好，现在我可懂了。我……我辞职！

  这个笑话告诉我们三个描述数据位置的参数之间的差别。

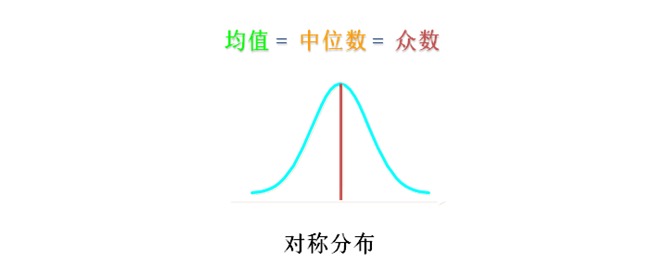
  通常来说，如果统计分布是对称的，且最高点在中间，那么均值、中位数和众数相等。

  

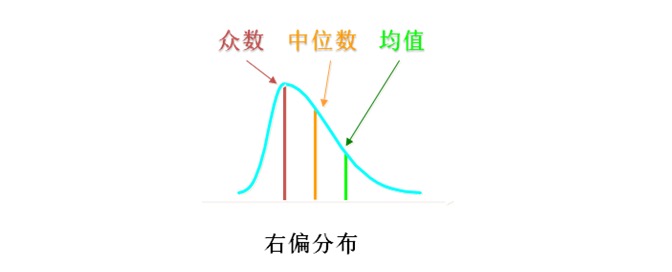
  如果统计分布右偏，即大部分集中在左边，右边拖着一个长长的尾巴——通常像楼价、国民收入等等都属于此类分布，则一般来说均值＞中位数＞众数，这时只看均值可能会比较片面，需要三个参数全看，以帮助你对数据进而对研究对象有全面地认识。

  

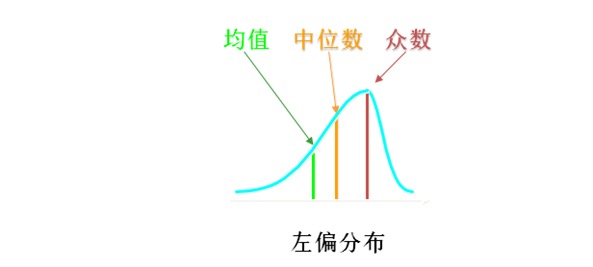
  有右偏肯定就有左偏分布，这时均值＜中位数＜众数。

  

  在这个例子里，分布是这样的：

  

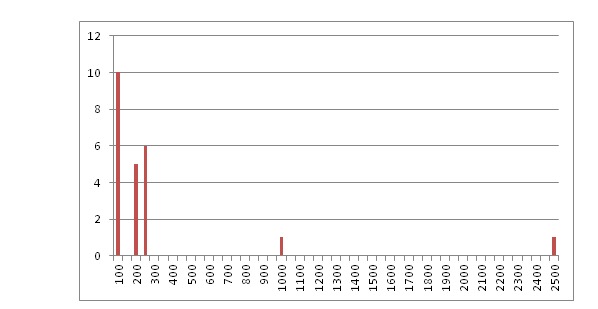
转载自 知乎 张老师漫谈六西格玛