সমন্বয়ের স্বজ্ঞাত বোধগম্যতা

এই নিবন্ধটি সমন্বয়ের ধারণার একটি স্বজ্ঞাত উপস্থাপনা প্রদান করে, যা আপনাকে এর মৌলিক অর্থ, এর প্রেরণা এবং এর সহজ প্রয়োগের দৃশ্যাবলী বুঝতে সাহায্য করে।

• সংযোজন

  এখানে আমি শুধু এই কথা বলতে চাই যে সমন্বয়ের সংজ্ঞাটি স্বজ্ঞাত, এবং এর সাথে জড়িত নয় কঠোর গাণিতিক চিহ্নের সংজ্ঞা এবং কঠোর সূত্রের অনুমান।

  যদি আপনি আগ্রহী হন, তাহলে উইকিপিডিয়া কোইন্টিগ্রেশন দেখুন। ভবিষ্যতে কোয়ান্টেশন ক্লাসরুমে কোইন্টিগ্রেশনের গভীরতা নিয়ে আলোচনা হবে।

  কেন সমতলতা/সংহতি?

  "এটি একটি অদ্ভুত ঘটনা, কিন্তু আমি মনে করি এটি একটি বড় ভুল ছিল।

  সহজভাবে বলতে গেলে, স্থিতিশীলতা (অস্থিরতা) একটি ধারাবাহিকতার একটি বৈশিষ্ট্য যা সময়ের সাথে স্থিতিশীল থাকে, এটি এমন একটি বৈশিষ্ট্য যা আমরা ডেটা বিশ্লেষণের পূর্বাভাস দেওয়ার সময় খুব পছন্দ করি। যদি কোনও সময়ক্রমের ডেটা সমতল থাকে তবে এর অর্থ হ'ল এর গড় এবং পার্থক্য অপরিবর্তিত থাকে, যাতে আমরা সহজেই কিছু পরিসংখ্যানগত কৌশল ব্যবহার করতে পারি।

  

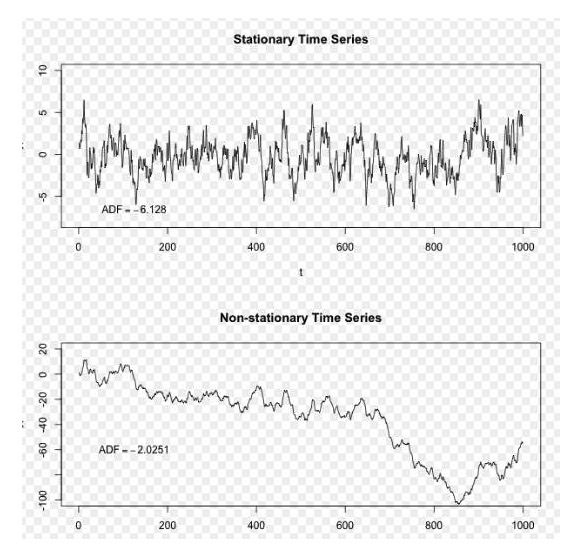
  ছবিঃ উইকিপিডিয়া

  উপরের ছবিতে, উপরের ক্রমটি একটি স্থিতিশীল ক্রম, যা আমরা দেখতে পাচ্ছি যে এটি সর্বদা একটি দীর্ঘমেয়াদী গড়ের চারপাশে ঘোরাফেরা করে, এবং নীচের ক্রমটি একটি অস্থির ক্রম, যা আমরা দেখতে পাচ্ছি যে এটির দীর্ঘমেয়াদী গড় পরিবর্তনশীল।

  উদাহরণস্বরূপ, যদি কোনও সম্পদের মূল্যের ধারাবাহিকতা (অথবা দুটি ধারাবাহিকতার মধ্যে মূল্যের পার্থক্য) স্থিতিশীল হয়, তবে যখন এটি তার গড় মান থেকে বিচ্যুত হয়, তখন আমরা আশা করতে পারি যে দামটি ভবিষ্যতে কোনও সময় এই গড় মানে ফিরে আসবে। আমরা এই বৈশিষ্ট্যটি বিনিয়োগের জন্য ব্যবহার করতে পারি এবং এর ফলে লাভ করতে পারি। ধরুন যে কোনও শেয়ারের দীর্ঘমেয়াদী গড় মূল্য 9 ডলার এবং বর্তমান মূল্য 8 ডলার। যদি পরীক্ষা করা হয় তবে আমরা মনে করি যে এই শেয়ারের historicalতিহাসিক ধারাবাহিকতা স্থিতিশীল এবং এই স্থিতিশীলতা বজায় রাখতে পারে, তবে আমরা এই শেয়ারটি কিনতে পারি এবং তার ভবিষ্যতের দাম 9 ডলার ফিরে আসার জন্য অপেক্ষা করতে পারি, যার ফলে 1 ডলার লাভ হয়।

  এখানে স্টক মূল্যের একটি ধারাবাহিক ধারাবাহিকতা রয়েছেঃ

  

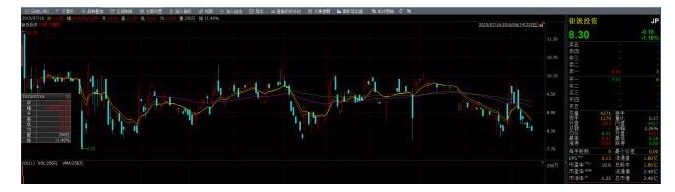
  সমান্তরালতা খুব ভাল কাজ করে, কিন্তু বাস্তবে, বেশিরভাগ স্টকই অ-সমান্তরাল, তাহলে আমরা কি সমান্তরালতার বৈশিষ্ট্যটি ব্যবহার করে লাভ করতে পারি? উত্তরটি হল হ্যাঁ, এই ক্ষেত্রে সমন্বয় সম্পর্ক ((cointegration) উপস্থিত হয়! যদি দুটি ক্রমের সেট সমান্তরাল না হয়, তবে তাদের লিনিয়ার সমন্বয় একটি সমান্তরাল ক্রম পেতে পারে, তাহলে আমরা বলি যে এই দুটি ক্রমের সময়সূচীর ডেটা সমান্তরাল বৈশিষ্ট্যযুক্ত, আমরা এই সমন্বয় ক্রমের উপর পরিসংখ্যানগত বৈশিষ্ট্যও ব্যবহার করতে পারি। তবে এটি উল্লেখ করা দরকার যে সমান্তরাল সম্পর্ক সম্পর্কযুক্ত সম্পর্ক নয় ((correlation)) ।

  উদাহরণস্বরূপ, যদি দুটি টাইম সিকোয়েন্সের তথ্যের মধ্যে পার্থক্য স্থিতিশীল থাকে, তবে আমরা এই পার্থক্যের স্থিতিশীলতার উপর ভিত্তি করে বিনিয়োগ করতে পারিঃ যখন দুটি শেয়ারের দামের পার্থক্য খুব বেশি হয়, স্থিতিশীলতার উপর ভিত্তি করে আমরা আশা করি যে দামের পার্থক্যটি সংযুক্ত হবে, তাই কম দামের শেয়ার কিনুন, উচ্চ মূল্যের শেয়ার বিক্রি করুন এবং দামের প্রত্যাবর্তনের জন্য অপেক্ষা করার সময় লাভের জন্য বিপরীত ক্রিয়াকলাপ করুন।

  তাই জোড়া ট্রেডিং শুরু হয়। এটা কি পরিষ্কার?

• স্থিতিশীলতা এবং পরীক্ষার পদ্ধতি

  কঠোরভাবে বলতে গেলে, স্থিতিশীলতাকে কঠোরভাবে স্টেশনারি এবং দুর্বল স্থিতিশীলতার মধ্যে বিভক্ত করা যেতে পারে। কঠোরভাবে স্থিতিশীলতা বলতে বোঝায় যে একটি ক্রম সর্বদা একটি অপরিবর্তিত বন্টন ফাংশন রয়েছে, এবং দুর্বল স্থিতিশীলতা বলতে বোঝায় যে ক্রমটির একটি অপরিবর্তিত ধ্রুবক বর্ণনামূলক পরিসংখ্যান রয়েছে। সমস্ত শক্তিশালী স্থিতিশীল ক্রম দুর্বল স্থিতিশীলতার বৈশিষ্ট্যটি পূরণ করে, তবে বিপরীতটি সত্য নয়। আমরা সাধারণত যা বলি তা দুর্বল স্থিতিশীলতা। সময়সূচী বিশ্লেষণে, আমরা সাধারণত ইউনিট রুট পরীক্ষার মাধ্যমে বিচার করি যে কোনও প্রক্রিয়া দুর্বল স্থিতিশীল কিনা।

  

  একটি অ্যাপ্লিকেশন উদাহরণ

  প্রথমত, এটা উল্লেখ করা প্রয়োজন যে সমন্বয় সম্পর্ক সম্পর্ক নয়। আমরা কৃত্রিমভাবে দুটি ডেটা সেট তৈরি করেছি, যার ফলে সমন্বয় সম্পর্কটি স্বজ্ঞাতভাবে দেখা যায়।
  import numpy as np
  import pandas as pd
  import seaborn
  import statsmodels
  import matplotlib.pyplot as plt
  from statsmodels.tsa.stattools import coint

  কনস্ট্রাকশন ডেটা

  প্রথমত, আমরা দুটি ডাটা সেট তৈরি করি, প্রতিটি ডাটা সেট 100। প্রথম সেট ডাটা হল 100 প্লাস একটি নেমে যাওয়া প্রবণতা এবং একটি স্ট্যান্ডার্ড নেগেটিভ বন্টন। দ্বিতীয় সেট ডাটা প্রথম সেট ডাটা ভিত্তিতে 30 যোগ করে এবং একটি অতিরিক্ত স্ট্যান্ডার্ড নেগেটিভ বন্টন যোগ করে।

  

  

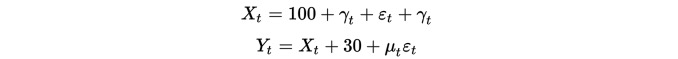
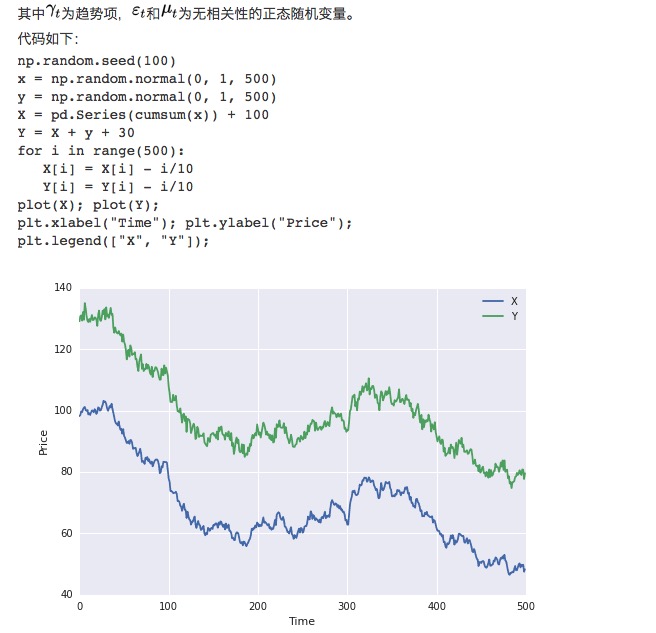
  স্পষ্টতই, এই দুটি ডাটা সেটই অ-সমতল, কারণ গড় মান সময়ের সাথে পরিবর্তিত হয়। তবে এই দুটি ডাটা সেট সমন্বয়যুক্ত, কারণ তাদের পার্থক্য ক্রম সমতলঃ

  plot(Y-X);
  plt.axhline((Y-X).mean(),color="red", linestyle="--");
  plt.xlabel("Time"); plt.ylabel("Price");
  plt.legend(["Y-X", "Mean"]);

  

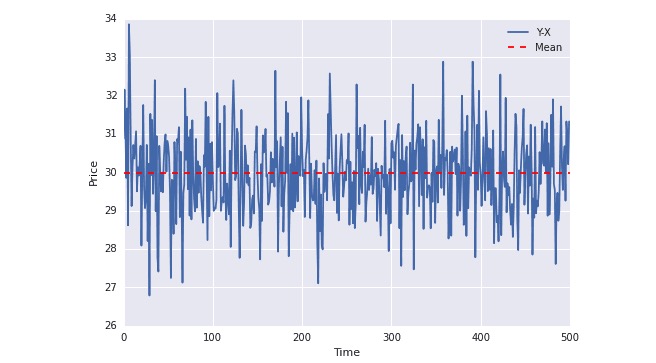
  উপরের চিত্র থেকে দেখা যাচ্ছে যে নীল রেখাটি সর্বদা গড়ের চারপাশে ঘোরাফেরা করে। গড়ের মান সময়ের সাথে পরিবর্তিত হয় না (বাস্তবে, গড়ও সময়ের সাথে পরিবর্তন হয় না) ।

• সংক্ষিপ্তসার

  যদি সমন্বয়কে সম্পূর্ণরূপে গাণিতিক দৃষ্টিকোণ থেকে ব্যাখ্যা করা হয়, তবে এটি আরও জটিল হবে, এবং ভবিষ্যতে কোয়ান্টামেশন ক্লাসগুলি এতে জড়িত হবে। আমরা কেবলমাত্র একটি সাধারণ ভূমিকা করেছি যা আমরা বুঝতে পারি (লেভেল-০) এবং আমাদের লক্ষ্য হ'ল সমন্বয়কে বাস্তব অ্যাপ্লিকেশনগুলির সাথে আরও ভালভাবে সংযুক্ত করা।

কোয়ান্টাম ক্লাস থেকে শেয়ার করুন