KNN অ্যালগরিদমের উপর ভিত্তি করে বেয়েসিয়ান শ্রেণিবদ্ধকারী

শ্রেণীবিভাগের সিদ্ধান্ত নেওয়ার জন্য শ্রেণীবিভাগের নকশার তাত্ত্বিক ভিত্তি বেয়েজ সিদ্ধান্তের তত্ত্বঃ

তুলনা করুন P ((ωiakamex) । যেখানেωi হল শ্রেণী i, x হল একটি পরিসংখ্যান যা পর্যবেক্ষণ করা হয়েছে এবং শ্রেণীবদ্ধ করা হয়েছে, P ((ωiakamex) এই পরিসংখ্যানের বৈশিষ্ট্যযুক্ত ভেক্টরগুলির ক্ষেত্রে এটির শ্রেণী i এর অন্তর্গত হওয়ার সম্ভাবনা কত তা বোঝায়। এটিও পরিণতিগত সম্ভাব্যতা। বেয়েস সূত্র অনুসারে, এটিকে এভাবে প্রকাশ করা যেতে পারেঃ

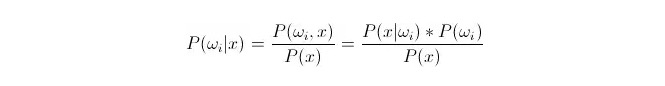
এর মধ্যে, P (x) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (i\) = \ (x\) = \ (x\) = \ (i\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = x\) । P (x\) = \ (x\) = \ (x\) = \ (x\) = \ (x\) = x\) । P (x) =

শ্রেণিবিন্যাসের সময়, প্রদত্ত x, যে শ্রেণীর জন্য পরিক্ষা প্রবণতা P ((ωiⴰⵙⴰⵙx) সবচেয়ে বড় তা নির্বাচন করা যেতে পারে। প্রতিটি শ্রেণীর জন্য P ((ωiⴰⵙx) ছোট হলে, ωi পরিবর্তনশীল এবং x স্থির; তাই P ((x) বাদ দেওয়া যেতে পারে, বিবেচনা না করে।

সুতরাং আমরা P (x) = P (x) = P*P ((ωi) প্রশ্ন। P ((ωi) হল প্রিভিলেজ সম্ভাব্যতা, যা শুধুমাত্র পরিসংখ্যানগত প্রশিক্ষণ কেন্দ্রে প্রতিটি শ্রেণিবদ্ধকরণের অধীনে প্রদর্শিত তথ্যের অনুপাতের উপর নির্ভর করে।

সম্ভবত সম্ভাব্যতা P (x < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i

নিম্নে k-প্রতিবেশী অ্যালগরিদম (ইংরেজিতে KNN) সম্পর্কে আলোচনা করা হল।

আমরা প্রশিক্ষণ কেন্দ্রের x1,x2…xn (যার প্রতিটি তথ্য m-মাত্রিক) তথ্যের উপর ভিত্তি করে, শ্রেণীωi এর অধীনে, এই তথ্যের বন্টনকে সামঞ্জস্য করি। x কে m-মাত্রিক স্থানের যেকোন একটি বিন্দু হিসাবে স্থাপন করে, কিভাবে P ((x ওωi) গণনা করা যায়?

আমরা জানি যে, যখন তথ্যের পরিমাণ যথেষ্ট বড় হয়, তখন অনুপাতগত ঘনিষ্ঠ সম্ভাব্যতা ব্যবহার করা যেতে পারে। এই নীতিটি ব্যবহার করে, পয়েন্ট x এর চারপাশে, পয়েন্ট x থেকে নিকটতম k নমুনা পয়েন্টগুলি খুঁজে বের করুন, যার মধ্যে শ্রেণী i এর কোনটি রয়েছে। এই k নমুনা পয়েন্টগুলিকে ঘিরে থাকা ক্ষুদ্রতম সুপারগোলের ভলিউম V গণনা করুন; অন্যথায় সমস্ত নমুনা ডেটাতে ওআই শ্রেণীর সংখ্যা Ni খুঁজে বের করুনঃ

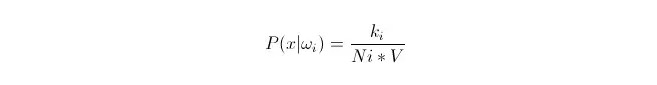
আপনি দেখতে পাচ্ছেন, আমরা আসলে x বিন্দুতে class-conditional probability density গণনা করেছি।

P (ωi) এর মানে কি? উপরের পদ্ধতি অনুসারে, P ((ωi) = Ni/N 。 যেখানে N হল নমুনার মোট সংখ্যা。 অন্যদিকে, P (x) =k/N*V), যেখানে k হল এই সুপারস্ফিয়ারের চারপাশের সমস্ত নমুনা পয়েন্টের সংখ্যা; N হল নমুনার সংখ্যা। সুতরাং P ((ωi 11:3x) কে গণনা করা যায়:

P(ωi|x)=ki/k

উপরের সমীকরণটি ব্যাখ্যা করার জন্য, একটি V- আকারের সুপারগ্লোবের মধ্যে, k টি নমুনাকে ঘিরে রাখা হয়েছে, যার মধ্যে i শ্রেণীর কোনটি রয়েছে। এইভাবে, কোন ধরণের নমুনা সবচেয়ে বেশি ঘিরে রাখা হয়েছে, আমরা সিদ্ধান্ত নেব যে এখানে x কোন শ্রেণীর অন্তর্গত হওয়া উচিত। এটি হল একটি শ্রেণিবিন্যাসকারী যা k কাছাকাছি প্রতিবেশী অ্যালগরিদম ডিজাইন করা হয়েছে।