কপিরাইট বিজ্ঞপ্তিঃ এই নিবন্ধের কোডটি পুনর্নির্মাণের জন্য দয়া করে উত্সটি উল্লেখ করুন, যদি বাণিজ্যিক ব্যবহারের জন্য হয় তবে ব্যক্তিগতভাবে লিখুন বা লেখকের সাথে যোগাযোগ করুনঃ [email protected]

1. ভূমিকা

কোয়ান্টাম ট্রেডিং এর সুবিধা

কোয়ান্টাম ট্রেডিং বলতে বোঝায় যে উন্নত গাণিতিক মডেলের পরিবর্তে মানুষের দ্বারা সৃষ্ট বিষয়বস্তুগত বিচার, কম্পিউটার প্রযুক্তি ব্যবহার করে বিপুল সংখ্যক historicalতিহাসিক ডেটা থেকে সমুদ্র নির্বাচন করতে পারে অতিরিক্ত উপার্জন নিয়ে আসে বিভিন্ন প্রবণতা প্রবণতা প্রবণতা প্রবণতা ঘটনা কৌশল তৈরি করতে, বিনিয়োগকারীদের মানসিকতার ওঠানামার প্রভাবকে ব্যাপকভাবে হ্রাস করে এবং বাজারের চরম উন্মত্ততা বা হতাশার ক্ষেত্রে অযৌক্তিক বিনিয়োগের সিদ্ধান্ত নেওয়া এড়ানো যায়। ডিজিটাল মুদ্রার কারণে ২৪*7 ঘন্টা অবিরাম লেনদেনের বাজারের ধারাবাহিকতা এবং পরিমাণগত লেনদেনের ফলে উচ্চ-ফ্রিকোয়েন্সি লেনদেনের প্রভাব অর্জন করা যায়, ডিজিটাল মুদ্রা বাজারের শুরু থেকে এটি স্পষ্টতই পরিমাণগতকরণের একটি ভাল শুরু। বর্তমানে ডিজিটাল মুদ্রা বাজারটি এখনও অপরিপক্ক। প্ল্যাটফর্ম লেনদেনের সিস্টেমের ক্র্যাশ, কে-লাইন প্লাগগুলি এখনও মাঝে মাঝে উপস্থিত হয়, এটি পরিমাণগত লেনদেনের জন্য একটি ঝুঁকি। তবে ডিজিটাল মুদ্রার জন্য পরিমাণগত লেনদেনের সামগ্রিক দিকটি এখনও লাভের চেয়ে বেশি। কারণ মডেলের প্রশিক্ষণের সময় এবং ধারাবাহিকতার পুনর্বিবেচনার মাধ্যমে আমরা স্বল্পতম সময়ে শত শত মডেলের মধ্যে সবচেয়ে উপযুক্ত পদ্ধতিটি চেষ্টা করতে পারি।

২। GQNR মডেলের সংক্ষিপ্ত বিবরণ

এই মডেলটি গার্চ মডেলের উপর ভিত্তি করে উদ্বায়ীতা পূর্বাভাস দেয়, যা অস্থিরতা পূর্বাভাসের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের ভ্যারিয়েন্টের উপর ভিত্তি করে তৈরি করা হয়।

1. গার্চ মডিউল

এই বিভাগে, আমরা গার্চের মূল সূত্রটি বিশদভাবে আলোচনা করব, যা আর্থিক বাজারে সর্বজনীন এবং ডিজিটাল মুদ্রার ক্ষেত্রে কিছু পূর্বাভাস কার্যকারিতা অর্জন করতে পারে।

1.1 গার্চের সংজ্ঞা

ARCH মডেলের মূল বিষয় হল অবশিষ্টাংশের বর্গক্ষেত্রের ক্রম ব্যবহার করে q-স্তরের চলমান সমতলটি বর্তমানের বিভাজন ফাংশন মানের সাথে সামঞ্জস্যপূর্ণ। যেহেতু চলমান গড় মডেলের স্ব-সম্পর্কিত ফ্যাক্টর q-স্তরের অন্তর্ভুক্তি রয়েছে, তাই ARCH মডেলটি কেবলমাত্র স্ব-সম্পর্কিত ফ্যাক্টরগুলির স্বল্পমেয়াদী স্ব-সম্পর্কিত ফ্যাক্টরগুলির জন্য প্রযোজ্য। কিন্তু বাস্তবে, কিছু অবশিষ্ট ক্রমের বৈষম্যমূলক ফাংশন দীর্ঘমেয়াদী স্বার্থপরতা রয়েছে, যখন ARCH মডেলের সাথে মিলিত বৈষম্যমূলক ফাংশন ব্যবহার করা হয়, তখন এটি উচ্চতর চলমান গড়কে উত্পন্ন করে, প্যারামিটার অনুমান করা আরও কঠিন করে তোলে এবং শেষ পর্যন্ত ARCH মডেলের মিলনের নির্ভুলতা প্রভাবিত করে।          সমস্যাটি সংশোধন করার জন্য, একটি বিস্তৃত স্ব-রিটার্ন কন্ডিশনাল ডিফারেনশিয়াল মডেল প্রস্তাব করা হয়েছে, যা সংক্ষিপ্তভাবে GARCH ((p,q) নামে পরিচিত। GARCH মডেলটি আসলে ARCH এর উপর ভিত্তি করে তৈরি করা হয়েছে, যার p-বর্গের স্বতঃ-রিটার্নযোগ্যতা যুক্ত করা হয়েছে যা বৈষম্যমূলক ফাংশন বিবেচনা করে, যা কার্যকরভাবে দীর্ঘমেয়াদী মেমোরির বৈষম্যমূলক ফাংশনকে সামঞ্জস্য করতে পারে। ARCH মডেলটি GARCH মডেলের একটি বিশেষ উদাহরণ, p=0 এর GARCH ((p,q) মডেল) ।

১.২ ARCH প্রক্রিয়া

       সংজ্ঞায়িত σn হল n-তম ট্রেডিং চক্রের মধ্যে সম্পদটির অস্থিরতা অনুমান করা হয়, mu হল দৈনিক আয়, তারপর সর্বশেষ m ট্রেডিং চক্রের আয় উপর ভিত্তি করে একটি পক্ষপাতহীন অনুমান করা যেতে পারেঃ $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         নিম্নলিখিত পরিবর্তনগুলি করুন 1μn-i কে শতাংশের হার হিসাবে রূপান্তর করুন;2m-1কে m হিসাবে রূপান্তর করুন;3μ = 0 অনুমান করুন এবং এই পরিবর্তনগুলি ফলাফলের উপর খুব বেশি প্রভাব ফেলবে না, উপরের সূত্র অনুসারে, অস্থিরতা হ্রাস করা যেতে পারেঃ \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         অর্থাৎ, প্রতিটি চক্রের ওঠানামার হারের বর্গক্ষেত্রের সমান ওজনের 1/m রয়েছে, যেহেতু এটি বর্তমান ওঠানামার অনুমান করা হয়, নিকটবর্তী ডেটাকে আরও বেশি ওজন দেওয়া উচিত, তাই উপরের সূত্রটি পরিবর্তন করা যেতে পারেঃ \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi হল i র্থ লেনদেনের চক্রের রিটার্ন স্কোয়ারের সহগ, যা ধনাত্মক এবং i এর মান যত ছোট হবে, তত বেশি ওজনের যোগফল হবে 1। আরও প্রসারিত করে, ধরে নিই যে একটি দীর্ঘমেয়াদী বৈষম্য VL রয়েছে, এবং এর ওজনের মান γ, উপরের সূত্র অনুসারে পাওয়া যাবেঃ

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        যাতেω=γVL, সূত্র(১৫) এইভাবে লিখতে পারেনঃ $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\(         উপরোক্ত সূত্রের ভিত্তিতে আমরা একটি সাধারণ ARCH () 1) প্রক্রিয়া পেতে পারি \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

১.৩ গার্চ প্রক্রিয়া

GARCH (p,q) মডেলটি ARCH (p) এবং EWMA (q) মডেলের সংমিশ্রণ, যার অর্থ হল অস্থিরতা কেবলমাত্র পূর্ববর্তী p-পর্বের উপার্জনের সাথে সম্পর্কিত নয়, বরং পূর্ববর্তী q-পর্বের সাথে সম্পর্কিত। $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         উপরের সূত্র অনুসারে আমরা একটি সাধারণ গার্চ পেতে পারিঃ \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

২ QR মডিউল

        এই বিভাগে মৌলিক ভগ্নাংশের পুনরাবৃত্তি এবং কৌশলগত ভগ্নাংশের গুরুত্ব বর্ণনা করা হবে

২.১ কিউআর সংজ্ঞা

বিভাগীয় রিটার্ন হল একটি পদ্ধতি যা একটি বিভাগীয় পরিবর্তনশীল X এবং ব্যাখ্যা করা পরিবর্তনশীল Y এর বিভাগীয় সংখ্যার মধ্যে একটি রৈখিক সম্পর্ক অনুমান করে। পূর্ববর্তী রিটার্ন মডেলগুলি আসলে ব্যাখ্যা করা ভেরিয়েবলের শর্তসাপেক্ষ প্রত্যাশা নিয়ে গবেষণা করা হয়। এবং লোকেরা ব্যাখ্যা করা ভেরিয়েবলের মধ্যম সংখ্যা এবং ব্যাখ্যা করা ভেরিয়েবলের বন্টনের সাথে ডিগ্রিগুলির কী সম্পর্ক রয়েছে তা নিয়েও উদ্বিগ্ন। এটি প্রথম কোয়েঙ্কার এবং বাসেট (1978) দ্বারা উত্থাপিত হয়েছিল। ওএলএস রিটার্নের অনুমানগুলি হ্রাসযোগ্য প্রতিবন্ধকতার বর্গক্ষেত্রের উপর ভিত্তি করে গণনা করা হয়। ডিগ্রি রিটার্নের অনুমানগুলি একটি অ-সম্মত ফর্মের উপর ভিত্তি করে নিখুঁত অবশিষ্ট প্রতিবন্ধকতা সংক্ষিপ্তকরণের উপর ভিত্তি করে গণনা করা হয়।

২.২ ওএলএস থেকে কিউআর

        সাধারণ রিগ্রেশন পদ্ধতি হল সর্বনিম্ন বিয়োগফল, যা সর্বনিম্ন ত্রুটির বর্গফলের সমষ্টিঃ $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         এবং ভগ্নাংশের লক্ষ্য হল উপরের সূত্রের উপর ভিত্তি করে ওজনযুক্ত ত্রুটির সর্বনিম্ন পরম মান এবংঃ \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

২.২ কিউআর ভিজ্যুয়ালাইজেশন

        আপনি দেখতে পারেন, সব নমুনা রেডিয়েশন লাইন দ্বারা বিভক্ত করা হয় বিভিন্ন স্থান, এবং এই রেডিয়েশন লাইন এছাড়াও একটি বিভাজক লাইন

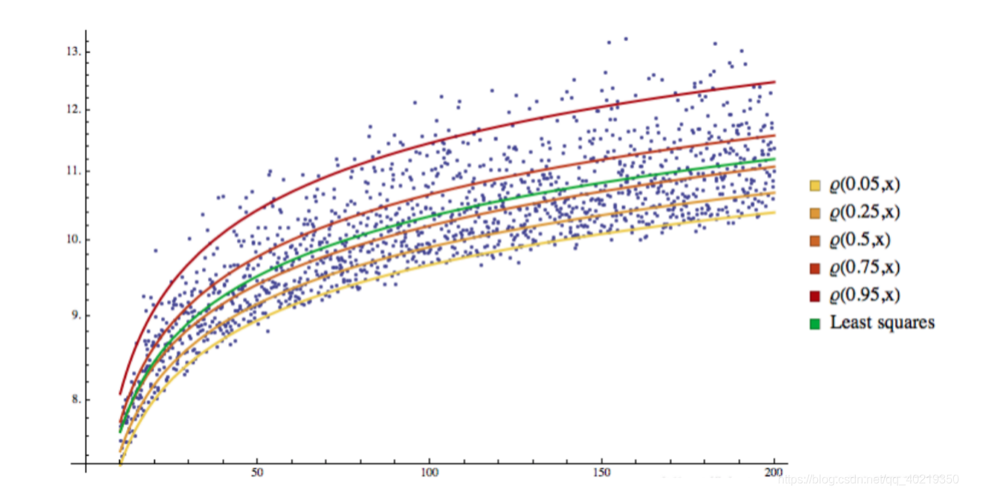
৩. গার্চ-কিউআর রিটার্ন

আমরা স্বাভাবিকভাবেই ভাবছিলাম যে, কি বাজারের অজানা ওঠানামা সিগমা এবং ভাজিলিয়াল Q অর্থাৎ VaR এর সাথে রিগ্রেশন করে ভবিষ্যতে সম্ভাব্যতার পরিস্থিতিতে ওঠানামা কমে যাওয়ার পূর্বাভাস দেওয়া যায়, এই সেক্টরটি এই দিক থেকে চলবে।

৩.১ ভোল্টেবল হার এবং ভ্যারিয়েবল রিটার্ন ফর্ম নির্বাচন করা

############################################################################################################################################################################################################################################################### $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

৩.২ লক্ষ্য ফাংশন নির্ধারণ

        উপরোক্ত তথ্যের উপর ভিত্তি করে, আমরা সমন্বয় করার পরে আমাদের চূড়ান্ত অপ্টিমাইজেশনের লক্ষ্য ফাংশন পেতে পারিঃ $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

৩.৩ মেশিন লার্নিং ব্যবহার করে লক্ষ্য ফাংশন অপ্টিমাইজ করা

এই ধাপে আরো কিছু বিকল্প রয়েছে, ঐতিহ্যগতভাবে, গ্রেডিয়েন্ট কমে যায়, এবং জিনগত অ্যালগরিদম ব্যবহার করা যেতে পারে, পাঠকরা তাদের নিজস্ব সৃজনশীলতা নিয়ে পরীক্ষা-নিরীক্ষা করতে পারেন। এখানে আমরা একটি অপ্টিমাইজড জিএ অ্যালগরিদম ব্যবহার করেছি, যা অন্য একটি ব্লগে বিস্তারিতভাবে বর্ণনা করা হয়েছে এবং এখন আর ব্যবহার করা হচ্ছে না।GA অ্যালগরিদম ঠিকানা সম্পর্কে

তৃতীয়ত, কিভাবে GQNR ব্যবহার করা যায়?

১. ধারণার স্থায়ীত্ব

        GQNR এর মূল বিষয় হল বাজারের অস্থিরতা, প্রতিটি বর্তমান সময়ের পয়েন্টে, পরবর্তী সময়ের অস্থিরতার জন্য গার্চ দ্বারা পূর্বাভাস দেওয়া যেতে পারে, অন্যদিকে, অতীতের ডেটা দ্বারা অস্থিরতার পূর্বাভাসের ভগ্নাংশের রিটার্নের মাধ্যমে, একটি উচ্চ-সম্ভাব্যতার সীমানা এবং নিম্ন-সীমানা অতিক্রম করবে না এমন একটি ওভারলেস থ্রেশহোল্ড পাওয়া যায়। এবং এই দুটি সীমানা, যা সামগ্রিকভাবে মূল। একবার উপরের সীমানা ট্রিগার করা হলে, আমরা মনে করতে পারি যে উচ্চ-সম্ভাব্যতার নীচে স্বল্প-মেয়াদী প্রবণতা রয়েছে, একবার নীচের সীমানা ট্রিগার করা হলে, আমরা মনে করতে পারি যে উচ্চ-সম্ভাব্যতার নীচে স্বল্প-মেয়াদী প্রবণতা রয়েছে।

২. ব্যবহারের অসুবিধা

• পুনরাবৃত্তি ফর্ম গ্রহণ
• অভিযোজনযোগ্য অ্যালগরিদমের পছন্দ
• মেশিন লার্নিং এর জন্য উপযুক্ত প্যারামিটার
• বাজারের অনিশ্চয়তা এবং এলোমেলোতা

৩। সমাধান

• কৌশল শেখার সময়সীমা কমানো
• দীর্ঘমেয়াদী ঝুঁকি প্রতিরোধে একক আমানতের গ্যারান্টি হ্রাস করুন
• ডাবল সমান্তরাল প্রবণতা সহ-নিশ্চিতকরণ এবং দ্বিতীয় অবমূল্যায়ন নিশ্চিতকরণ