টাইমিং কৌশল নির্বাচন ((1) ক্লাসিকাল প্রযুক্তিগত সূচক নির্বাচন করার সময় Z রূপান্তর দৃষ্টিকোণ নীচের নিম্ন বিলম্ব প্রবণতা লাইন গঠন

কিছুক্ষন আগে, কেউ কেউ আমার সম্পর্কে বলেছিলেন যে আমি প্রতিদিন একটি কুকুরের কৌশল বিকাশ করি, হ্যাঁ, কুকুরের কৌশল শেষ হয়ে গেছে। আজ আমি আপনাদের সাথে শেয়ার করছি একটি কুকুরের সাম্প্রতিক ব্যবহারের কৌশল (doge) ।১. পূর্বশর্ত ● আসুন আসুন আসল বিষয়ের দিকে একটু গুরুত্ব সহকারে যাই, ক্লাসিকাল টাইমিং কৌশলগুলি আসলে কয়েকটি প্রধান বিভাগে বিভক্তঃ স্বল্পমেয়াদী ইভেন্ট চালিত (যা মুদ্রার বৃত্তে প্রধান এক্সচেঞ্জের বিজ্ঞপ্তি এবং টুইটগুলি পর্যবেক্ষণ করে, পাঠ্য বিশ্লেষণের সাথে জড়িত), পরিসংখ্যানগতভাবে প্রত্যাবর্তন এবং পূর্বাভাস (পরিসংখ্যানগত সুবিধাগুলি, সমন্বয়যুক্ত লেনদেন, বিভিন্ন এমএল এবং ডিএল মডেল, স্তরিত লুকানো মার্কভ ইত্যাদি), জিএসআইএসআই বিভাগের বিনিয়োগকারীদের আবেগ এবং traditionalতিহ্যবাহী ক্লাসিকাল প্রযুক্তিগত সূচকগুলির জন্য।

N日移动平均线=N日收盘价之和/N

● এই জিনিসটি সাধারণভাবে সাধারণ বিনিয়োগকারীদের কাছে এমএ নামে পরিচিত, একটি সমতল লাইন, যা কেনা-বেচা করে, বিক্রি করে এবং অসংখ্য * বীজ এক্সচেঞ্জের জন্য তাদের প্রসেসিং ফি প্রদান করে। ● সমান্তরাল রেখা মূল্যের গতিবিধি ভালভাবে বর্ণনা করতে পারে এবং এই প্রবণতাটি ঘনিষ্ঠভাবে অনুসরণ করতে পারে এবং এটি সহজেই পরিবর্তন হয় না। ফিউচার সিটিএ-র বিকাশে, সমান্তরাল রেখা একটি অত্যন্ত গুরুত্বপূর্ণ রেফারেন্স সূচক বলে মনে করা যেতে পারে। যাইহোক, সাধারণ বিনিয়োগকারীদের জন্য সমান্তরাল রেখার ব্যবহারের জন্য নিম্নলিখিত কয়েকটি সমস্যা রয়েছেঃ প্রথমত, সমান্তরাল রেখার বিলম্ব গুরুতর, প্রায়শই যখন প্রবণতা দেখা দেয় তখন প্রবণতা অর্ধেক চলে গেছে এবং ফিরে আসে; দ্বিতীয়ত, মুদ্রাচক্রের সাধারণ বিনিয়োগকারীরা প্রায়শই আংশিক স্তরের সূচকগুলির সাথে ঘড়ি পরিচালনা করেন, 15,5 মিনিট, 5 মিনিট এমনকি 1 মিনিট, এত ছোট চক্রের মধ্যে, মুদ্রাচক্রের 80% এরও বেশি বৈশিষ্ট্যযুক্ত কম্পন (মার্টিনের পছন্দসই প্রবণতা) । ● এই নিবন্ধটি একটি অ্যালগরিদম তৈরি করার লক্ষ্যে তৈরি করা হয়েছে যা সমতল শ্রেণীর সূচকগুলিকে ফিল্টার করে এবং তাদের বিলম্বকে হ্রাস করে।

Z রূপান্তর, পাস ফাংশন ● এই নিবন্ধের আগে, আমি বিভিন্ন বড় ওয়েবসাইটে পরিমাপকারী ফিল্টারিং অ্যালগরিদম সম্পর্কে কিছু শিখেছি, যেমন সর্বাধিক প্রচলিত ট্রিপল ফিল্টারিং ((স্কিউডার ব্রডকাস্টের কয়েকটি সিটিএতে উপস্থিত হয়) এবং জয়েনকোয়ান্টের উপর লেখকের গবেষণা করা কার্লম্যান ফিল্টারিং পদ্ধতিটি ২০১৫ সালের শেয়ার বিপর্যয় থেকে সফলভাবে পালিয়ে গেছে। টিবিতে ইআর ফিল্টারিং মডিউল রয়েছে যা ব্যবহার করা অত্যন্ত সুবিধাজনক। তবে যখন আমি আবিষ্কার করেছি যে জয়েনকোয়ান্টে সরবরাহ করা কার্লম্যান ফিল্টারিং মডিউলটি সার্ভারে ইনস্টল করা যায় না এবং এটির ওপেন সোর্স কোডের কয়েক হাজার লাইন রয়েছে, তখন জিও এটিকে মুদ্রাচক্রের মধ্যে স্থানান্তর করার চেষ্টা ত্যাগ করেছে। Z রূপান্তরিত ফিল্টারিং একটি সহজ বিকল্প। ● Z রূপান্তরটি ল্যাপারস থেকে এসেছে এবং এটি সাধারণত গণিতের সংকেত প্রক্রিয়াকরণের ক্ষেত্রে ব্যবহৃত হয়। একটি বিচ্ছিন্ন সময় ক্রম f ((k) এবং বহু-ফ্রিকোয়েন্সি ডোমেইনে সংজ্ঞায়িত z এর জন্য, এর সূত্রটি নিম্নরূপ সংজ্ঞায়িত করা হয়েছেঃ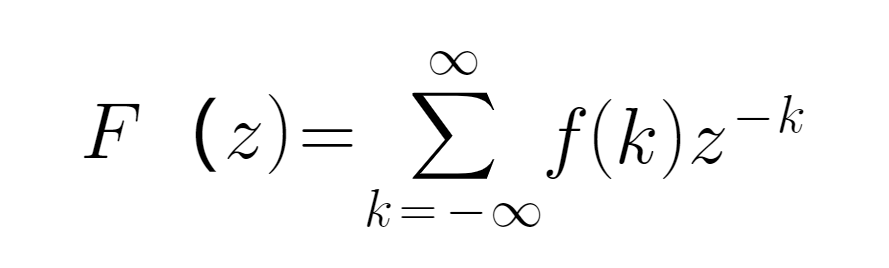

● ইএমএ সমতলটি এমএ এর তুলনায় কম বিলম্বিত হয় ((মূলত এটি ইডব্লিউএমএ অ্যালগরিদমের মাধ্যমে এমএ সিরিজটি প্রক্রিয়া করার পরে পাওয়া ফলাফল), তাই আমরা এখানে এমএ সিরিজটি এমএ এর পরিবর্তে ব্যবহার করি, যাতে ফিল্টারিংয়ের প্রভাব বাড়ানো যায়। আমরা ইনপুটটি মুদ্রার দাম হিসাবে সংজ্ঞায়িত করি ((বন্ধের দাম), p হিসাবে লিখিত), এবং আউটপুটটি দামের সাথে সামঞ্জস্যপূর্ণ ইএমএ সূচক হিসাবে লিখিত হয়, যা ইএমএ হিসাবে লিখিত হয় ((z) । অতএব, এখানে প্রেরণ ফাংশনটি মূলত মুদ্রার ইএমএ এবং এর সাথে সামঞ্জস্যপূর্ণ প্রেরণ মূল্যের তীব্রতার অনুপাত, এটি একটি প্রতিক্রিয়াশীল সিস্টেম, প্রেরণ ফাংশনটি হজ হিসাবে লিখিতঃ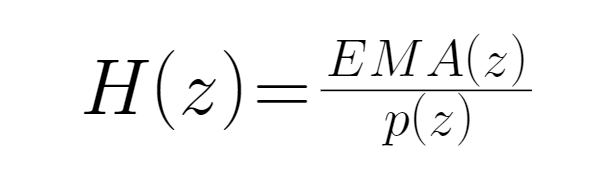

● EWMA এর অ্যালগরিদমের মধ্যে এই সূত্রটি ইনপুট করুন, যা EMA এর প্রাথমিক প্রেরণ ফাংশন প্রদান করেঃ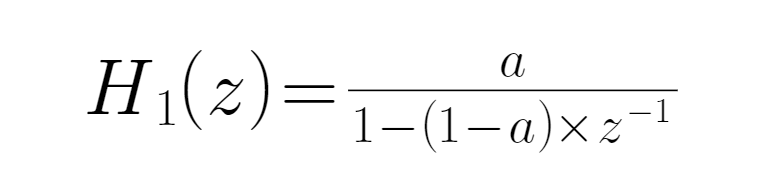

● যেখানে a একটি পরিবর্তনশীল প্যারামিটার, যা নিম্নলিখিতটির সাথে সমান।

৩. পাস ফাংশন বিশ্লেষণ ● ট্রান্সমিশন ফাংশনে, ইনপুট সিগন্যাল ফাংশন মানের সাথে সম্পর্কিত হয় না; এটি ফাংশনের বিশ্লেষণ দ্বারা জানা যায় যে, যখন z ** -1 = -1, H ((z) সর্বাধিক মান গ্রহণ করে, তখন সর্বোচ্চ ফ্রিকোয়েন্সিতে পৌঁছে যায়, ট্রান্সমিশন ফাংশনটি H ((z) = a/ ((2-a) হয়, সাম্প্রতিক উচ্চ-ফ্রিকোয়েন্সি ডেটার শব্দটি সর্বাধিক হ্রাস পায়; যখন z ** -1 = 1, H ((z) একটি ধ্রুবক, তখন সিস্টেমের ফ্রিকোয়েন্সি 0 হয়, তখন ইনপুট এবং আউটপুট ফলাফলগুলি পুরোপুরি একই হয়, যদি এই সময় সিরিজটি একটি ধ্রুবক সিরিজ হয়, তবে EMA এখানে থাকবে। ● যখন H (((z) একটি নিম্ন-পরিবাহী ফিল্টার এবং H (((z) = 1, তখন আউটপুট সিগন্যালটি সমস্ত ইনপুট সিগন্যালের ভগ্নাংশ ধারণ করে, অর্থাৎ সমস্ত আউটপুট সিগন্যালের মধ্যে, যদি সমস্ত নিম্ন-ফ্রিকোয়েন্সি সিগন্যালগুলি বিয়োগ করা হয়, তবে 1-H ((z) একটি নতুন ফিল্টার হিসাবে গঠিত হতে পারে, যা H 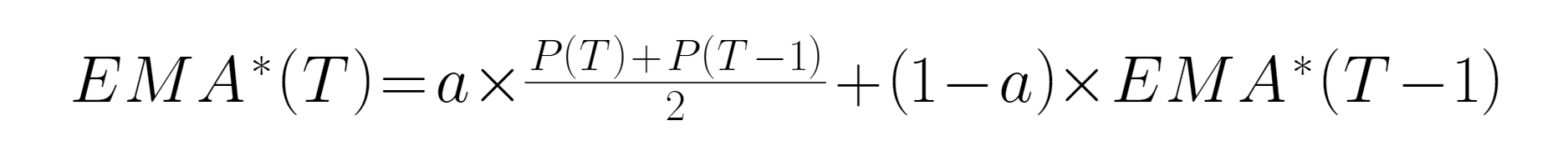((z) হিসাবে চিহ্নিত করা হয়, যা H ((z) এর বিপরীতে, এটি একটি উচ্চ-পরিবাহী ফিল্টার। ● P ((T) কে মুদ্রার রুট k এর দাম হিসাবে মনে রাখবেন, আমরা আজকের দাম এবং আগের দিনের দাম নিয়ে এই ফাংশন সম্পর্কিত ফর্মুলাটি মসৃণ করি, যাতে আউটপুট ইএমএ-তে আরও সংশোধন করা যায়। (এটি হ'ল মূল ট্রান্সমিশন ফাংশন H ((z) = a/(2-a) এ উচ্চ ফ্রিকোয়েন্সি সংকেতটি কার্যকরভাবে ফিল্টার করা হয়নি, তাই একটি মান আগে নেওয়া হয় যাতে এটি মসৃণ করা যায়, যদি ফলাফলটি খারাপ হয় তবে আরও কয়েকটি ওজন নেওয়া যায়) তাই দিনের জন্য ইনপুট করা ইএমএ সংশোধন অভিব্যক্তিটি হ'লঃ● এই অভিব্যক্তিটি নিম্ন-পরিবাহী ফিল্টার এবং উচ্চ-পরিবাহী ফিল্টারগুলির জন্য 1 দ্বারা বিয়োগ করা দরকারঃ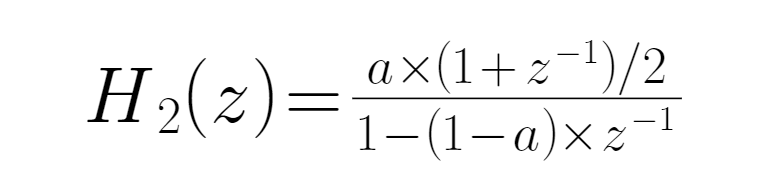● এখন ফিল্টারটির এক্সপ্রেশন তৈরি করা হয়েছে! Z রূপান্তর দ্বারা, আমরা একটি কম বিলম্বের প্রবণতা লাইন তৈরি করতে পারি, এবং এটি কেবলমাত্র একটি প্যারামিটার a, a এর বৃহত্তর, কম বিলম্ব, আরও ভাল মসৃণতা। বিভিন্ন জাতের জন্য, তাদের নিজস্ব উপযুক্ত প্যারামিটার রয়েছে।

৪. সংক্ষিপ্ত বিবরণ এবং মনোযোগ ● উপরের ধাপে নির্মিত ফিল্টারটি কেবলমাত্র এক স্তরের, এবং এটির ফিল্টারিংয়ের প্রভাব খুব আদর্শ নয়, কারণ ট্রানজিশন বেল্ডটি খুব দীর্ঘ, এবং স্তরের সংখ্যা বাড়ানোর পরে, H ((z) ফাংশন এক্সপ্রেশনগুলির জটিলতা সূচকীয় স্তরে বৃদ্ধি পায়, খুব উচ্চ স্তরের ক্ষেত্রেও ফিল্টারিংয়ের অভিন্নতা অনিয়মিত ঝাঁপিয়ে পড়ার সম্ভাবনা রয়েছে। অতীতের অভিজ্ঞতা থেকে দেখা যায় যে, দ্বিতীয় বা তৃতীয় স্তরটি আরও উপযুক্ত স্তর, পাঠক নিজেও একটি রৈখিক সংমিশ্রণ ব্যবহার করে একাধিক একই বা বিভিন্ন স্তরের ফিল্টারকে সিরিয়াল করতে পারেন এবং এর প্রভাবটি পর্যবেক্ষণ করতে পারেন। ● এই Z রূপান্তর-ভিত্তিক ফিল্টারিং অ্যালগরিদমটি কেবলমাত্র সমতল শ্রেণীর সূচকগুলির জন্য প্রযোজ্য নয়, সমস্ত মিথ্যা সংকেতের সূচক যেমন বল এবং এট্রির মাধ্যমে ফিল্টারিং অ্যালগরিদমের মাধ্যমে একটি নির্দিষ্ট ফিল্টারিং প্রভাব অর্জন করা যেতে পারে, যা দরপত্রের আকার নির্ধারণ করে, যার ফলে মূল সূচকের বিলম্বের গুরুতর পরিণামগুলি হ্রাস পায়। • এই নিবন্ধটি একটি অনুচ্ছেদ শেষ করে, এটির সাথে সম্পর্কিত অ্যালগরিদম কোড সরবরাহ করার সময় নেই, তবে কেবল একটি ধারণা দেওয়া হয়েছে যা আগ্রহী পাঠকরা নিজেরাই পরীক্ষা করতে পারেন।

● Promise Quant মিনো মার্টিন-কেন্দ্রিক বিভিন্ন ধরনের অদ্ভুত কুকুরের কৌশল বিকাশের উপর দৃষ্টি নিবদ্ধ করে, যেমন যদি আপনার ভাড়া বা বড় তহবিল পরিচালনার প্রয়োজন হয় তবে vx:15001733415 এ যোগাযোগ করুন