গত সপ্তাহে পরিচয়VaR ঝুঁকি ব্যবস্থাপনাযখন উল্লেখ করা হয় যে একটি পোর্টফোলিওর ঝুঁকি পৃথক সম্পদের ঝুঁকির সমান নয়, এটি তাদের মূল্যের সম্পর্কের সাথে সম্পর্কিত। একটি উদাহরণ হিসাবে দুটি সম্পদ নিন, যদি তাদের ইতিবাচক পারস্পরিক সম্পর্ক খুব শক্তিশালী হয়, অর্থাৎ, তারা একসাথে বৃদ্ধি পায়, তাহলে বহুমুখী বিনিয়োগ ঝুঁকি কমাতে পারে না যদি নেতিবাচক সম্পর্ক শক্তিশালী হয়, বৈচিত্রপূর্ণ বিনিয়োগ ঝুঁকি কমাতে পারে। স্বাভাবিক প্রশ্ন হল, পোর্টফোলিওতে বিনিয়োগ করার সময়, ঝুঁকির একটি নির্দিষ্ট স্তরে কীভাবে সর্বোচ্চ আয় করা যায়? আমাদের মার্কোভিটজ তত্ত্ব ব্যবহার করতে হবে যা আমরা আজ প্রবর্তন করব।

১৯৫২ সালে হ্যারি মার্কোভিটজ কর্তৃক প্রস্তাবিত আধুনিক পোর্টফোলিও তত্ত্ব (এমপিটি) হল পোর্টফোলিও নির্বাচনের জন্য একটি গাণিতিক কাঠামো যার লক্ষ্য হল ঝুঁকি নিয়ন্ত্রণের সময় বিভিন্ন ঝুঁকিপূর্ণ সম্পদের সংমিশ্রণ নির্বাচন করে প্রত্যাশিত রিটার্ন সর্বাধিক করা। মূল ধারণা হল সম্পদের দাম নিখুঁতভাবে পরিবর্তিত হয় না (অর্থাৎ, সম্পদের মধ্যে একটি অসম্পূর্ণ সম্পর্ক রয়েছে), এবং সম্পদ বরাদ্দ বৈচিত্র্যকরণের মাধ্যমে সামগ্রিক বিনিয়োগ ঝুঁকি হ্রাস করা যেতে পারে।

মার্কোভিটজ তত্ত্বের মূল ধারণা

1. প্রত্যাশিত রিটার্ন হার: এটি একটি বিনিয়োগকারী একটি সম্পদ বা পোর্টফোলিও ধারণ থেকে প্রাপ্তির আশা করতে পারে, সাধারণত ঐতিহাসিক রিটার্ন ডেটার উপর ভিত্তি করে ভবিষ্যদ্বাণী করা হয়।

   \(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

   এর মধ্যে, \(E(R_p)\) হল বিনিয়োগ পোর্টফোলিওর প্রত্যাশিত রিটার্ন, \(w_i\) হল বিনিয়োগ পোর্টফোলিওতে \(i\)-তম সম্পদের ওজন, \(E(R_i)\) হল \( এর প্রত্যাশিত রিটার্ন i\)-তম সম্পদ।

2. ঝুঁকি (অস্থিরতা বা আদর্শ বিচ্যুতি): বিনিয়োগের রিটার্নের অনিশ্চয়তা বা বিনিয়োগের অস্থিরতা পরিমাপ করতে ব্যবহৃত হয়।

   \(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

   যেখানে \(\sigma_p\) হল পোর্টফোলিওর মোট ঝুঁকি এবং \(\sigma_{ij}\) হল সম্পদ \(i\) এবং সম্পত্তি \(j\)-এর সমপরিমাণ, যা দুটি সম্পদের মধ্যে মূল্য চলাচলের সম্পর্ক পরিমাপ করে।

3. সহবাস: দুটি সম্পদের মধ্যে মূল্য পরিবর্তনের মধ্যে পারস্পরিক সম্পর্ক পরিমাপ করে।

   \(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

   তাদের মধ্যে, \(\rho_{ij}\) হল সম্পদের পারস্পরিক সম্পর্ক সহগ \(i\) এবং সম্পদ \(j\), \(\sigma_i\) এবং \(\sigma_j\) হল যথাক্রমে সম্পদ \(i\) এবং সম্পদ \(j\) এর আদর্শ বিচ্যুতি।

4. দক্ষ সীমান্ত: ঝুঁকি-রিটার্ন সমন্বয় ব্যবস্থায়, দক্ষ সীমান্ত হল পোর্টফোলিওগুলির সেট যা ঝুঁকির একটি নির্দিষ্ট স্তরে সর্বাধিক প্রত্যাশিত রিটার্ন প্রদান করতে পারে।

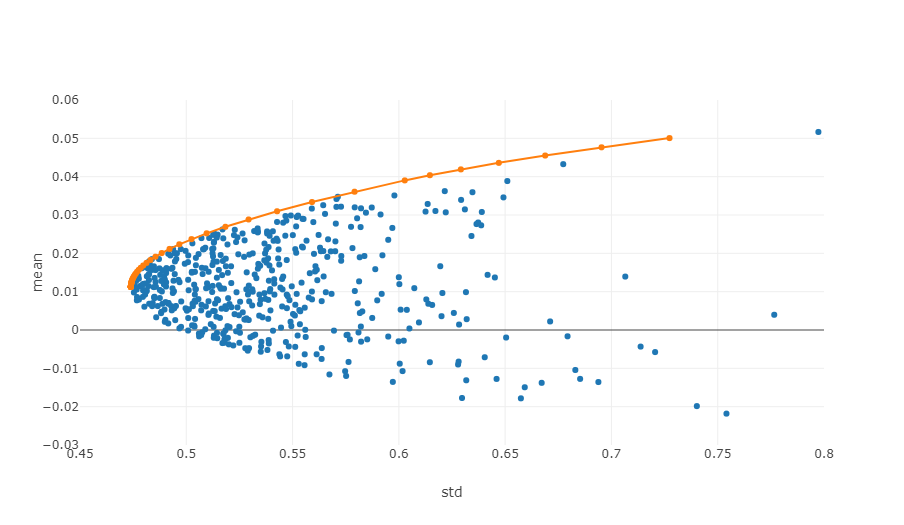
উপরের ছবিটি কার্যকর সীমান্তের একটি পরিকল্পিত চিত্র। প্রতিটি বিন্দু বিভিন্ন ওজন সহ একটি বিনিয়োগ পোর্টফোলিওকে প্রতিনিধিত্ব করে। অনুভূমিক অক্ষ হল অস্থিরতা, অর্থাৎ ঝুঁকির স্তর, এবং উল্লম্ব অক্ষ হল রিটার্নের হার। স্পষ্টতই, আমরা গ্রাফের উপরের প্রান্তের উপর ফোকাস করি, যা একই ঝুঁকি স্তরে সর্বোচ্চ রিটার্ন অর্জন করে।

পরিমাণগত ট্রেডিং এবং পোর্টফোলিও পরিচালনায়, এই নীতিগুলি প্রয়োগ করার জন্য ঐতিহাসিক ডেটার পরিসংখ্যানগত বিশ্লেষণের প্রয়োজন হয়, গাণিতিক মডেল ব্যবহার করে প্রত্যাশিত রিটার্ন, মানক বিচ্যুতি এবং বিভিন্ন সম্পদের সমপরিমাণ অনুমান করতে হয়। তারপরে, অপ্টিমাইজেশন কৌশলগুলি সর্বোত্তম সম্পদ ওজন বরাদ্দ খুঁজে পেতে প্রয়োগ করা হয়। এই প্রক্রিয়ায় সাধারণত জটিল গাণিতিক ক্রিয়াকলাপ এবং প্রচুর কম্পিউটার প্রক্রিয়াকরণ জড়িত থাকে, যে কারণে আধুনিক আর্থিক ক্ষেত্রে পরিমাণগত বিশ্লেষণ অত্যন্ত গুরুত্বপূর্ণ হয়ে উঠেছে। কীভাবে অপ্টিমাইজ করা যায় তা বোঝাতে নিম্নলিখিতগুলি নির্দিষ্ট পাইথন উদাহরণগুলি ব্যবহার করবে।

সিমুলেশন পদ্ধতি ব্যবহার করে সর্বোত্তম সমন্বয় খুঁজে পেতে পাইথন কোড উদাহরণ

মার্কোভিটজ সর্বোত্তম পোর্টফোলিও গণনা করা একটি বহু-পদক্ষেপ প্রক্রিয়া, এতে ডেটা প্রস্তুতি, সিমুলেটেড ইনভেস্টমেন্ট পোর্টফোলিও এবং সূচকগুলির গণনার মতো গুরুত্বপূর্ণ পদক্ষেপগুলি জড়িত। রেফারেন্স: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. বাজারের তথ্য পান：

   • পাসget_dataনির্বাচিত ডিজিটাল মুদ্রার ঐতিহাসিক মূল্য ডেটা প্রাপ্ত করার ফাংশন। এটি রিটার্ন এবং ঝুঁকি গণনা করার জন্য প্রয়োজনীয় ডেটা, যা পোর্টফোলিও তৈরি করতে এবং শার্প অনুপাত গণনা করতে ব্যবহৃত হয়।

2. রিটার্ন এবং ঝুঁকি গণনা：

   • ব্যবহারcalculate_returns_riskফাংশনটি প্রতিটি ডিজিটাল মুদ্রার বার্ষিক রিটার্ন এবং বার্ষিক ঝুঁকি (মান বিচ্যুতি) গণনা করে। এটি সর্বোত্তম সংমিশ্রণে ব্যবহারের জন্য প্রতিটি সম্পদের ঐতিহাসিক কর্মক্ষমতা পরিমাপ করা।

3. মার্কোভিটজের সর্বোত্তম পোর্টফোলিও গণনা করুন：

   • ব্যবহারcalculate_optimal_portfolioফাংশন, একাধিক পোর্টফোলিওর অনুকরণ। প্রতিটি সিমুলেশনে, সম্পদের ওজন এলোমেলোভাবে তৈরি করা হয় এবং পোর্টফোলিওর প্রত্যাশিত রিটার্ন এবং ঝুঁকি এই ওজনের উপর ভিত্তি করে গণনা করা হয়।
   • এলোমেলোভাবে বিভিন্ন ওজনের সংমিশ্রণ তৈরি করে, সেরাটি খুঁজে পেতে একাধিক সম্ভাব্য পোর্টফোলিও অন্বেষণ করা যেতে পারে। এটি মার্কোভিটজের পোর্টফোলিও তত্ত্বের মূল ধারণাগুলির মধ্যে একটি।

পুরো প্রক্রিয়াটির লক্ষ্য হল এমন পোর্টফোলিও খুঁজে বের করা যা নির্দিষ্ট ঝুঁকির স্তরের জন্য সর্বোত্তম প্রত্যাশিত রিটার্ন দেয়। একাধিক সম্ভাব্য সংমিশ্রণ অনুকরণ করে, বিনিয়োগকারীরা বিভিন্ন কনফিগারেশন কীভাবে কাজ করবে তা আরও ভালভাবে বুঝতে পারেন এবং তাদের বিনিয়োগের উদ্দেশ্য এবং ঝুঁকি সহনশীলতার জন্য সবচেয়ে উপযুক্ত সংমিশ্রণটি বেছে নিতে পারেন। এই পদ্ধতি বিনিয়োগের সিদ্ধান্তগুলিকে সর্বোত্তম করে তুলতে এবং বিনিয়োগকে আরও দক্ষ করে তুলতে সাহায্য করে।

            
            
            
import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
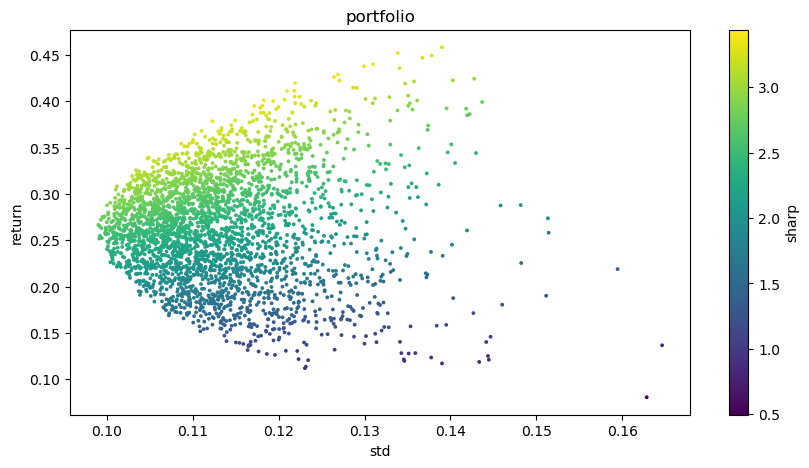
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

চূড়ান্ত ফলাফল:
সর্বোত্তম সংমিশ্রণ:
BTCUSDT ওজন: 0.0721
ETHUSDT ওজন: 0.2704
BNBUSDT ওজন: 0.3646
LINKUSDT ওজন: 0.1892
BCHUSDT ওজন: 0.0829
LTCUSDT ওজন: 0.0209
প্রত্যাশিত রিটার্নের হার: ০.৪১৯৫
প্রত্যাশিত ঝুঁকি (মান বিচ্যুতি): 0.1219
তীক্ষ্ণ অনুপাত: ৩.৪৪০৩