বেয়েজ - সম্ভাব্যতার রহস্য, সিদ্ধান্তের পিছনে গাণিতিক জ্ঞানের সন্ধান

বেয়েজ পরিসংখ্যান হল গণিতের একটি শক্তিশালী বিশ্ববিদ্যালয় শাখা, যা আর্থিক, চিকিৎসা গবেষণা এবং তথ্য প্রযুক্তি সহ অনেক ক্ষেত্রে ব্যাপকভাবে প্রয়োগ করা হয়। এটি আমাদের পূর্ববর্তী বিশ্বাসগুলিকে প্রমাণের সাথে একত্রিত করতে এবং পরবর্তী বিশ্বাসগুলি তৈরি করতে সক্ষম করে যা আমাদের আরও জ্ঞানী সিদ্ধান্ত নিতে সক্ষম করে।

এই নিবন্ধে, আমরা কিছু প্রধান গণিতবিদদের সংক্ষিপ্ত পরিচয় করিয়ে দেব যারা এই ক্ষেত্রের প্রতিষ্ঠাতা।

বেয়েজ এর আগে বেয়েজীয় পরিসংখ্যানকে আরও ভালভাবে বোঝার জন্য, আমাদের ১৮শ শতাব্দীতে ফিরে যেতে হবে এবং গণিতবিদ ডি মোইভ্রে এবং তার গবেষণায় সুযোগের মূলনীতির কথা উল্লেখ করতে হবে।

তার গবেষণাপত্রে, ডি মোভ্রে তার যুগের অনেকগুলি সম্ভাব্যতা এবং জুয়া সম্পর্কিত সমস্যা সমাধান করেছিলেন। যেমনটি আপনি সম্ভবত জানেন, তার একটি সমস্যার সমাধান স্বাভাবিক বন্টনের উৎপত্তি ঘটায়, তবে এটি অন্য গল্প।

তার গবেষণায় সবচেয়ে সহজ একটি প্রশ্ন ছিলঃ

আপনি যদি একটি ন্যায্য মুদ্রা ব্যবহার করে তিনটি ধারাবাহিক মুদ্রা নিক্ষেপ করেন, তাহলে আপনি তিনটি ইতিবাচক সম্ভাবনা পাবেন।

আপনি সম্ভবত লক্ষ্য করেছেন যে জয়ের নিয়মাবলীতে বর্ণিত সমস্যাগুলি পড়লে আপনি লক্ষ্য করবেন যে বেশিরভাগ সমস্যা একটি অনুমান দিয়ে শুরু হয় এবং তারপরে প্রদত্ত ইভেন্টের সম্ভাবনা গণনা করে। উদাহরণস্বরূপ, উপরের সমস্যাটিতে একটি অনুমান রয়েছে যে মুদ্রাটি ন্যায্য, সুতরাং জয়ের ক্ষেত্রে একটি ইতিবাচক সম্ভাবনা 0.5।

এটি আজকে গণিতের ভাষায় বলা হয়ঃ

𝑃(𝑋|𝜃)

কিন্তু যদি আমরা জানি না যে এই মুদ্রাটি ন্যায্য কিনা?𝜃এটা কি?

টমাস বেয়েজ এবং রিচার্ড প্রাইস

প্রায় পঞ্চাশ বছর পরে, ১৭৬৩ সালে, একটি সমস্যা সমাধানের মূলনীতিতে একটি সমস্যা সমাধানের জন্য একটি থীম তৈরি করা হয়, যার নাম ছিল 'কনফ্লোসিয়াল ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং ফাইন্ডিং'।

ডকুমেন্টের প্রথম কয়েক পৃষ্ঠায়, গণিতবিদ রিচার্ড প্রাইসের লেখা একটি লেখা রয়েছে যা তার বন্ধু টমাস বেয়েসের মৃত্যুর কয়েক বছর আগে লেখা একটি গবেষণার বিষয়বস্তুর সংক্ষিপ্ত বিবরণ দেয়।

তিনি আরও বলেন, 'আমি মনে করি, আমাদের মধ্যে একটি সমস্যা আছে।

একটি অজানা ঘটনা ঘটে এবং ব্যর্থ হয় কতবার, তার সম্ভাবনা যে কোন দুটি নামকরণ সম্ভাব্যতা মধ্যে খুঁজে পাওয়া যায়;

অন্য কথায়, আমরা একটি ঘটনা পর্যবেক্ষণ করার পর, আমরা একটি অজানা প্যারামিটার খুঁজে পাই।θদুইটি সম্ভাব্যতার মধ্যে সম্ভাব্যতা কত? এটি আসলে ইতিহাসের অন্যতম প্রথম প্রশ্ন যা পরিসংখ্যানগত অনুমানের সাথে সম্পর্কিত এবং এটি নামটি ফিরিয়ে দেয় বিপরীত সম্ভাব্যতা।

𝑃( 𝜃 | 𝑋）

অবশ্যই, এটিই আমরা আজকে বেয়েজ থিওরি নামে পরিচিত একটি পটভূমি বিতরণ।

অকারণ কারণ

এই দুই প্রবীণ যাজক সম্পর্কে জানতে চাইলে,টমাস বেয়েজএবংরিচার্ড প্রাইসতবে এটি করার জন্য, আমাদেরকে সাময়িকভাবে পরিসংখ্যান সম্পর্কে কিছু জ্ঞান ছেড়ে দিতে হবে।

আমরা ১৮শ শতাব্দীতে আছি, এবং সম্ভাব্যতা গণিতবিদদের জন্য ক্রমবর্ধমান আগ্রহের একটি ক্ষেত্র হয়ে উঠছে। ডেমোফার বা বার্নুলির মতো গণিতবিদরা দেখিয়েছেন যে কিছু ঘটনা কিছু পরিমাণে এলোমেলোভাবে ঘটে, কিন্তু এখনও নির্দিষ্ট নিয়ম দ্বারা নিয়ন্ত্রিত হয়। উদাহরণস্বরূপ, যদি আপনি একাধিকবার জ্যাক করেন, তবে ষষ্ঠের এক ভাগ সময় এটি ছয়টিতে থামবে। এটি যেন একটি গোপন নিয়ম রয়েছে যা সুযোগের ভাগ্য নির্ধারণ করে।

এখন, কল্পনা করুন যে আপনি একজন গণিতবিদ এবং এই সময়ে বসবাসকারী ধর্মপ্রাণ বিশ্বাসী। আপনি এই গোপন নিয়ম এবং ঈশ্বরের সম্পর্ক সম্পর্কে জানতে আগ্রহী হতে পারেন।

এটি প্রকৃতপক্ষে বেজ এবং প্রাইসের নিজের প্রশ্ন। তারা এই সমস্যার সমাধানের জন্য সরাসরি প্রয়োগ করতে চান যে জ্যোতির্বিশ্বকে অবশ্যই বুদ্ধি এবং বুদ্ধিমত্তার ফলাফল হতে হবে; অতএব, চূড়ান্ত কারণের সাথে Godশ্বরের অস্তিত্বের প্রমাণ প্রদান করুন[2] - অর্থাৎ, কারণহীন কারণ।

ল্যাপারাস

আশ্চর্যজনকভাবে, প্রায় দুই বছর পরে, ১৭৭৪ সালে, টমাস বেয়েজের একটি কাগজ পড়ার পরে, ফরাসি গণিতবিদ ল্যাপারস একটি কাগজ লিখেছিলেন, যার নাম ছিল "The Cause of Related Events by the Probability of Events"[3]। এটি ছিল বিপরীত সম্ভাব্যতার সমস্যা সম্পর্কে একটি কাগজ। প্রথম পৃষ্ঠায় আপনি পড়তে পারেনঃ

মূল নীতিঃ

যদি একটি ঘটনা n টি ভিন্ন কারণের দ্বারা সৃষ্ট হতে পারে, তবে প্রদত্ত ঘটনার জন্য এই কারণগুলির সম্ভাব্যতা একে অপরের মধ্যে অনুপাতের সমান হবে, যা প্রদত্ত কারণের ঘটনার সম্ভাব্যতা, এবং এই কারণগুলির প্রতিটির অস্তিত্বের সম্ভাব্যতা সমান হবে, যা প্রদত্ত ঘটনার কারণের সম্ভাব্যতা, এই কারণগুলির প্রতিটি ঘটনার সম্ভাব্যতার যোগফলকে ছাড়িয়ে।

এটি বেয়েজের তত্ত্ব যা আমরা আজ জানিঃ

​

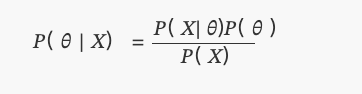
এর মধ্যেP(θ)এটি একটি সমতুল্য বন্টন।

মুদ্রা পরীক্ষা

আমরা পাইথন এবং PyMC ল্যাবরেটরি ব্যবহার করে বেয়েজ পরিসংখ্যানকে এখন পর্যন্ত নিয়ে যাব এবং একটি সহজ পরীক্ষা করব।

ধরুন, আপনার বন্ধু আপনাকে একটি মুদ্রা দেয় এবং জিজ্ঞেস করে যে আপনি কি মনে করেন যে এটি একটি ন্যায্য মুদ্রা। তিনি তাড়াহুড়ো করছেন এবং তিনি আপনাকে বলে যে আপনি কেবল 10 টি মুদ্রা নিক্ষেপ করতে পারেন। আপনি দেখতে পারেন, এই সমস্যার একটি অজানা প্যারামিটার রয়েছে।pএবং আমরা এটাকে অনুমান করতে চাই যে, যদি আপনি একটি পয়েন্টের মধ্যে একটি ধনাত্মক পয়েন্ট পেতে চান,pএটি একটি সম্ভাব্য মান।

(দ্রষ্টব্যঃ আমরা প্যারামিটার বলছি না)pএটি একটি র্যান্ডম ভেরিয়েবল, কিন্তু এই প্যারামিটারটি স্থির, আমরা জানতে চাই যে এটি কোন মানের মধ্যে সবচেয়ে সম্ভবত।)

এই প্রশ্নের বিভিন্ন দৃষ্টিভঙ্গির জন্য, আমরা এটিকে দুটি ভিন্ন পূর্বনির্ধারিত বিশ্বাসের ভিত্তিতে সমাধান করবঃ

• ১। আপনি মুদ্রার ন্যায্যতা সম্পর্কে পূর্বের কোন তথ্য নেই, এবং সমান সম্ভাব্যতা বরাদ্দp◊ এই ক্ষেত্রে, আমরা তথাকথিত তথ্যহীন পূর্ববর্তী ব্যবহার করব, কারণ আপনি আপনার বিশ্বাসের মধ্যে কোনও তথ্য যুক্ত করেননি।

• ২। আপনি অভিজ্ঞতার মাধ্যমে জানেন যে মুদ্রা যদি অন্যায়ও হতে পারে, তবে এটিকে অত্যন্ত অন্যায় করা কঠিন।pসম্ভবত ০.৩ এর চেয়ে কম বা ০.৭ এর চেয়ে বেশি হবে না; এই ক্ষেত্রে, আমরা একটি তথ্য পূর্বশর্ত ব্যবহার করব।

এই দুইটি ঘটনার ক্ষেত্রে, আমাদের পূর্ববর্তী বিশ্বাসগুলি হ'লঃ

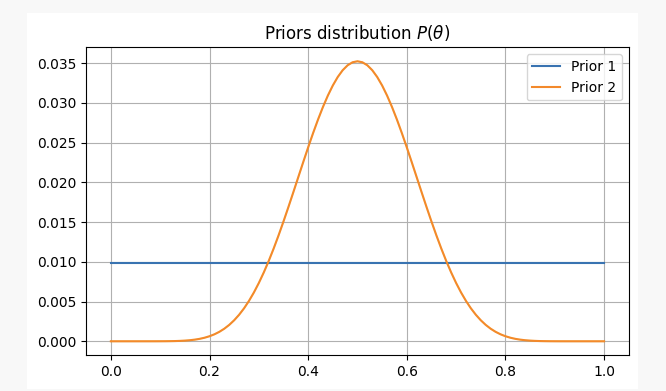
আপনি যদি ১০ বার মুদ্রা ছোঁড়েন, তাহলে আপনি ২ বার ইতিবাচক ফলাফল পাবেন। এই প্রমাণ দিয়ে, আমরা সম্ভবত আমাদের পরামিতিগুলি কোথায় পাব।p？

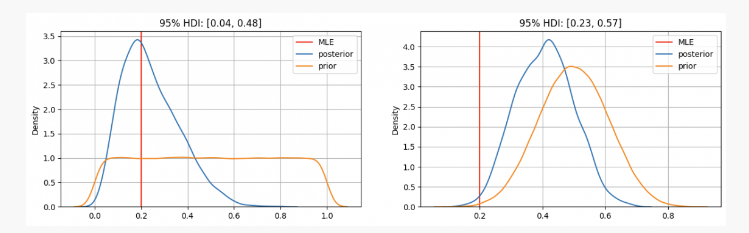
আপনি দেখতে পাচ্ছেন, প্রথম ক্ষেত্রে আমরা প্যারামিটারগুলোকেpপূর্ববর্তী বন্টনটি সর্বাধিক অনুরূপ অনুমান (এমএলই) এর উপর কেন্দ্রীভূতp=0.2, যা ফ্রিকোয়েন্সি স্কুল পদ্ধতি ব্যবহারের অনুরূপ পদ্ধতি। সত্য অজানা পরামিতিগুলি 95% বিশ্বাসযোগ্যতার মধ্যে থাকবে, 0.04 এবং 0.48 এর মধ্যে।

অন্যদিকে, একটি উচ্চ নির্ভরযোগ্যতা আছে যে পরামিতিp0.3 এবং 0.7 এর মধ্যে হওয়া উচিত, আমরা 0.4 এর আশেপাশে একটি ব্যাকট্র্যাক বিতরণ দেখতে পাচ্ছি, যা আমাদের এমএলই দ্বারা প্রদত্ত মানের চেয়ে অনেক বেশি; এই ক্ষেত্রে সত্য অজানা পরামিতিগুলি 95% বিশ্বাসযোগ্যতার মধ্যে থাকবে, 0.23 এবং 0.57 এর মধ্যে।

সুতরাং, প্রথম ক্ষেত্রে, আপনি আপনার বন্ধুকে বলবেন যে আপনি নিশ্চিত যে মুদ্রাটি ন্যায্য নয়। কিন্তু অন্য ক্ষেত্রে, আপনি তাকে বলবেন যে আপনি নিশ্চিত নন যে মুদ্রাটি ন্যায্য কিনা।

আপনি দেখতে পাচ্ছেন যে, একই প্রমাণের (১০ টির মধ্যে ২ টি ইতিবাচক) পরেও, বিভিন্ন পূর্ববর্তী বিশ্বাসের অধীনে ফলাফলগুলি ভিন্ন হতে পারে। এটি বেয়েজ পরিসংখ্যানের একটি সুবিধা, বৈজ্ঞানিক পদ্ধতির মতো, এটি আমাদের পূর্ববর্তী বিশ্বাসগুলিকে নতুন পর্যবেক্ষণ এবং প্রমাণের সাথে একত্রিত করে আমাদের বিশ্বাসগুলি আপডেট করতে দেয়।

END

আজকের নিবন্ধে, আমরা বেয়েজ পরিসংখ্যানের উৎপত্তি এবং এর প্রধান অবদানকারীদের দিকে নজর রাখব।转载自quantdare.com。