ARMA-EGARCH মডেলের উপর ভিত্তি করে বিটকয়েনের অস্থিরতার মডেলিং এবং বিশ্লেষণ

সম্প্রতি, আমি বিটকয়েনের অস্থিরতা সম্পর্কে কিছু বিশ্লেষণ করেছি, যা শব্দযুক্ত এবং স্বতঃস্ফূর্ত। সুতরাং আমি কেবল আমার কিছু বোঝার এবং কোডটি নিম্নরূপ ভাগ করি। আমার ক্ষমতা সীমিত, এবং কোডটি খুব নিখুঁত নয়। যদি কোনও ভুল থাকে তবে দয়া করে এটি নির্দেশ করুন এবং সরাসরি এটি সংশোধন করুন।

১. অর্থনীতির সময়কালের সংক্ষিপ্ত বিবরণ

অর্থের সময় সিরিজ হল সময় মাত্রায় পর্যবেক্ষণ করা একটি পরিবর্তনশীল উপর ভিত্তি করে স্টোকাস্টিক প্রক্রিয়া সিরিজ মডেলগুলির একটি সেট। পরিবর্তনশীলটি সাধারণত সম্পদের রিটার্ন রেট। যেহেতু রিটার্ন রেট বিনিয়োগের স্কেল থেকে স্বাধীন এবং পরিসংখ্যানগত প্রকৃতির, তাই অন্তর্নিহিত আর্থিক সম্পদের বিনিয়োগের সুযোগ বিশ্লেষণ করা আরও মূল্যবান।

এখানে, এটি সাহসীভাবে অনুমান করা হয় যে বিটকয়েনের রিটার্ন রেট সাধারণ আর্থিক সম্পদের রিটার্ন রেট বৈশিষ্ট্যগুলির সাথে সামঞ্জস্যপূর্ণ, অর্থাৎ এটি একটি দুর্বলভাবে মসৃণ সিরিজ, যা বেশ কয়েকটি নমুনার ধারাবাহিকতা পরীক্ষার মাধ্যমে প্রদর্শিত হতে পারে।

১-১ প্রস্তুতি, আমদানি লাইব্রেরি, ইনক্যাপসুলার ফাংশন

গবেষণা পরিবেশের কনফিগারেশন সম্পূর্ণ হয়েছে। পরবর্তী গণনার জন্য প্রয়োজনীয় লাইব্রেরি এখানে আমদানি করা হয়। যেহেতু এটি বিরতিপূর্ণভাবে লেখা হয়, তাই এটি অপ্রয়োজনীয় হতে পারে। দয়া করে এটি নিজে পরিষ্কার করুন।

[1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

আউট[1]: {ব্যালেন্স : ১০০.০, ফ্রোজেনবালেন্স : ০.০, স্টক : ০.০, ফ্রোজেনস্টক : ০.০}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

[17] এঃ

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

১-২। আসুন বিটকয়েনের ঐতিহাসিক তথ্য সম্পর্কে সংক্ষিপ্ত ধারণা দিয়ে শুরু করি

পরিসংখ্যানগত দৃষ্টিকোণ থেকে, আমরা বিটকয়েনের কিছু ডেটা বৈশিষ্ট্য দেখতে পারি। উদাহরণস্বরূপ গত বছরের ডেটা বিবরণ গ্রহণ করে, রিটার্ন রেটটি সহজ উপায়ে গণনা করা হয়, অর্থাৎ বন্ধের মূল্য লোগারিথমিকভাবে বিয়োগ করা হয়। সূত্রটি নিম্নরূপঃ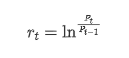

[3] এঃ

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

আউট[3]: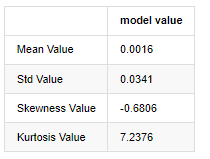

ঘন চর্বিযুক্ত লেজগুলির বৈশিষ্ট্যটি হ'ল সময়ের স্কেল যত কম হবে, বৈশিষ্ট্যটি তত বেশি গুরুত্বপূর্ণ। ডেটা ফ্রিকোয়েন্সির বৃদ্ধির সাথে সাথে কার্টোসিস বৃদ্ধি পাবে এবং বৈশিষ্ট্যটি উচ্চ-ফ্রিকোয়েন্সি ডেটাতে খুব সুস্পষ্ট হবে।

১লা জানুয়ারি, ২০১৯ থেকে বর্তমান পর্যন্ত প্রতিদিনের ক্লোজিং মূল্যের তথ্য উদাহরণ হিসেবে নিলে আমরা এর লোগারিদমিক রিটার্ন রেটের একটি বর্ণনামূলক বিশ্লেষণ করি, এবং দেখা যায় যে বিটকয়েনের সহজ রিটার্ন রেট সিরিজ স্বাভাবিক বন্টনের সাথে সামঞ্জস্যপূর্ণ নয়, এবং এটিতে ঘন চর্বিযুক্ত লেজগুলির সুস্পষ্ট বৈশিষ্ট্য রয়েছে।

ক্রমটির গড় মান 0.0016, মান বিচ্যুতি 0.0341, বিচ্যুতি -0.6819, এবং কুরটোস 7.2243, যা স্বাভাবিক বন্টনের তুলনায় অনেক বেশি এবং ঘন ফ্যাট লেজগুলির বৈশিষ্ট্যযুক্ত। বিটকয়েনের সাধারণ রিটার্ন রেটের স্বাভাবিকতা QQ চার্ট দিয়ে পরিমাপ এবং পরীক্ষা করা হয়, নিম্নরূপঃ

[4] এঃ

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

আউট[4]:

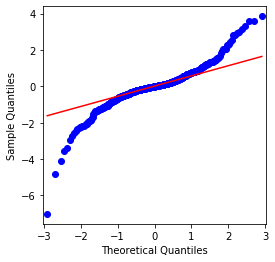
এটা দেখা যায় যে QQ চার্টটি নিখুঁত, এবং বিটকয়েনের লোগারিদমিক রিটার্ন সিরিজটি ফলাফল থেকে একটি স্বাভাবিক বন্টনের সাথে সামঞ্জস্যপূর্ণ নয়, এবং এটিতে ঘন চর্বিযুক্ত লেজগুলির সুস্পষ্ট বৈশিষ্ট্য রয়েছে।

এরপরে, আসুন আমরা উদ্বায়ীতা সমষ্টি প্রভাবটি দেখি, অর্থাৎ আর্থিক সময় সিরিজগুলি প্রায়শই বৃহত্তর উদ্বায়ীতার পরে বৃহত্তর উদ্বায়ীতার সাথে থাকে, যখন ছোট উদ্বায়ীতা সাধারণত ছোট উদ্বায়ীতার সাথে থাকে।

অস্থিরতা ক্লাস্টারিং অস্থিরতার ইতিবাচক এবং নেতিবাচক ফিডব্যাক প্রভাবগুলি প্রতিফলিত করে এবং এটি ফ্যাট লেজ বৈশিষ্ট্যগুলির সাথে অত্যন্ত সম্পর্কিত। অর্থাত, এর অর্থ হ'ল অস্থিরতার সময় সিরিজগুলি স্বয়ংক্রিয়ভাবে সম্পর্কিত হতে পারে, অর্থাৎ বর্তমান সময়ের অস্থিরতার পূর্ববর্তী সময়ের সাথে কিছু সম্পর্ক থাকতে পারে, দ্বিতীয় পূর্ববর্তী সময়কাল বা এমনকি তৃতীয় পূর্ববর্তী সময়কাল।

[5] এঃ

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

আউট[5]:

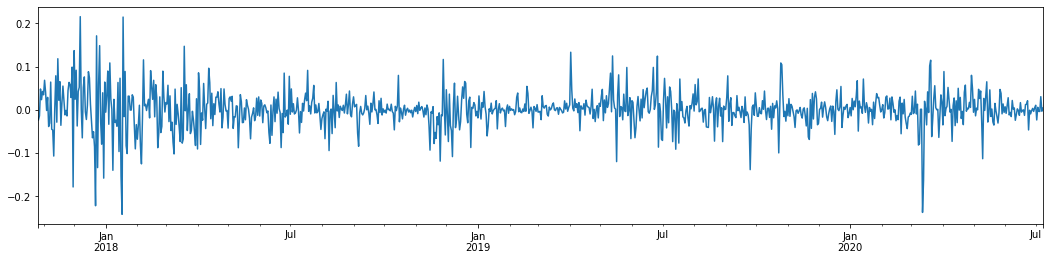
গত 3 বছরে বিটকয়েনের দৈনিক লগারিদমিক রিটার্ন রেট গ্রহণ করে এবং এটি প্লট করা হলে, অস্থিরতা ক্লাস্টারিংয়ের ঘটনাটি স্পষ্টভাবে দেখা যায়। 2018 সালে বিটকয়েনের ষাঁড়ের বাজারের পরে, এটি বেশিরভাগ সময় স্থিতিশীল অবস্থানে ছিল। যেমনটি আমরা চূড়ান্ত ডানদিকে দেখতে পাচ্ছি, 2020 সালের মার্চ মাসে, বিশ্বব্যাপী আর্থিক বাজারগুলি ধসে পড়ার সাথে সাথে বিটকয়েনের তরলতার উপরও একটি চাল ছিল, ফলনগুলি এক দিনের মধ্যে প্রায় 40% হ্রাস পেয়েছিল, তীব্র নেতিবাচক দোলগুলির সাথে।

সংক্ষেপে, স্বজ্ঞাত পর্যবেক্ষণ থেকে, আমরা দেখতে পাচ্ছি যে একটি বড় ওঠানামা একটি বড় সম্ভাবনার সাথে ঘন ওঠানামা দ্বারা অনুসরণ করা হবে, যা অস্থিরতার সমষ্টিগত প্রভাবও। যদি এই অস্থিরতার পরিসীমাটি পূর্বাভাসযোগ্য হয় তবে এটি বিটিসি এর স্বল্পমেয়াদী লেনদেনের জন্য মূল্যবান, যা অস্থিরতার বিষয়ে আলোচনা করার উদ্দেশ্যও।

১-৩। তথ্য প্রস্তুতি

প্রশিক্ষণ নমুনা সেট প্রস্তুত করার জন্য, প্রথমে, আমরা একটি বেঞ্চমার্ক নমুনা স্থাপন করি, যার মধ্যে লগারিদমিক রিটার্ন রেট সমতুল্য পর্যবেক্ষণযোগ্য অস্থিরতা। কারণ দিনের অস্থিরতা সরাসরি পর্যবেক্ষণ করা যায় না, ঘন্টা প্রতি ঘন্টা তথ্য পুনরায় নমুনা করার জন্য ব্যবহৃত হয়। দিনের বাস্তবায়িত অস্থিরতা অনুমান করতে এবং এটিকে অস্থিরতার নির্ভরশীল পরিবর্তনশীল হিসাবে গ্রহণ করুন।

পুনরায় নমুনা গ্রহণের পদ্ধতিটি ঘণ্টার তথ্যের উপর ভিত্তি করে। সূত্রটি নিম্নরূপ দেখানো হয়েছেঃ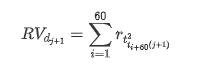

[4] এঃ

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

আউট[4]: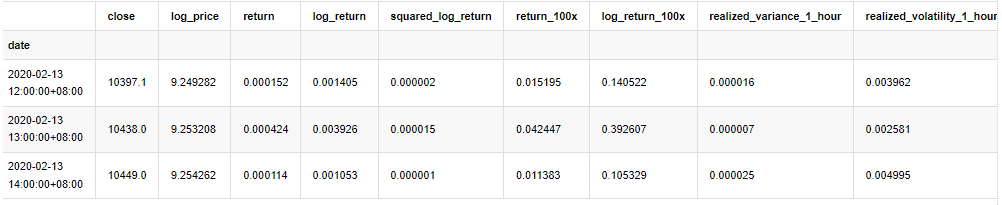

নমুনার বাইরে একই ভাবে ডেটা প্রস্তুত করুন

[5] এঃ

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

নমুনার মৌলিক তথ্য বোঝার জন্য, একটি সহজ বর্ণনামূলক বিশ্লেষণ নিম্নরূপ করা হয়ঃ

[৯] এঃ

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

আউট[9]:

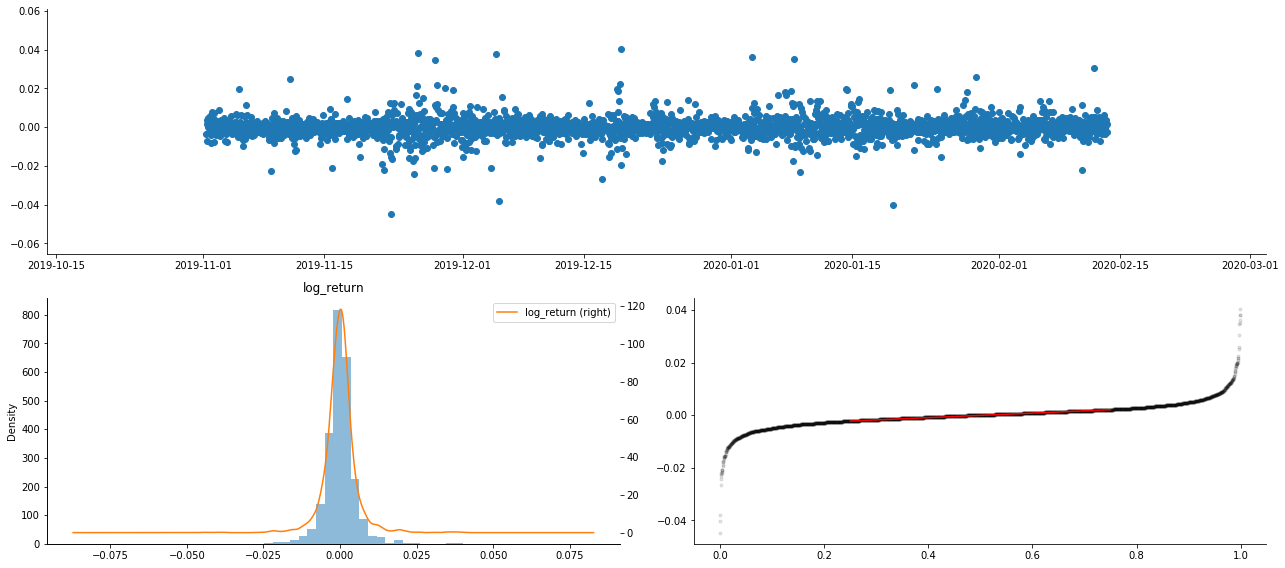
ফলস্বরূপ, লোগারিথমিক রিটার্নের টাইম সিরিজ চার্টে স্পষ্টভাবে অস্থিরতা সমষ্টি এবং লিভারেজ প্রভাব রয়েছে।

লোগারিদমিক রিটার্নের বন্টন চার্টে বিকৃতি 0 এর চেয়ে কম, যা নির্দেশ করে যে নমুনার রিটার্নগুলি সামান্য নেতিবাচক এবং ডানদিকে পক্ষপাতমূলক। লোগারিদমিক রিটার্নের QQ চার্টে, আমরা দেখতে পাচ্ছি যে লোগারিদমিক রিটার্নের বন্টন স্বাভাবিক নয়।

ডাটা বন্টনের বিকৃতি 1 এর চেয়ে কম, যা ইঙ্গিত দেয় যে নমুনার মধ্যে রিটার্নগুলি সামান্য ইতিবাচক এবং সামান্য ডানদিকে বিভ্রান্ত। কুরটোসিস মান 3 এর চেয়ে বড়, যা ইঙ্গিত দেয় যে ফলনটি ঘন চর্বিযুক্ত লেজ বিতরণ করা হয়েছে।

এখন যেহেতু আমরা এই পর্যায়ে পৌঁছেছি, আসুন আরেকটি পরিসংখ্যানগত পরীক্ষা করি। [৭] এঃ

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

আউট[7]:

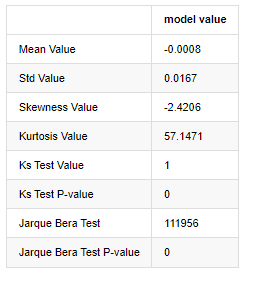
কলমোগোরভ-স্মিরনভ এবং জার্ক-বেরা পরীক্ষার পরিসংখ্যান যথাক্রমে ব্যবহৃত হয়। মূল অনুমানটি উল্লেখযোগ্য পার্থক্য এবং স্বাভাবিক বন্টনের দ্বারা চিহ্নিত করা হয়। যদি পি মান 0.05% আত্মবিশ্বাসের স্তরের সমালোচনামূলক মানের চেয়ে কম হয় তবে মূল অনুমানটি প্রত্যাখ্যান করা হয়।

এটি দেখা যায় যে কার্টোসিস মানটি 3 এর চেয়ে বড়, যা ঘন ফ্যাট লেজের বৈশিষ্ট্য দেখায়। কেএস এবং জেবি এর পি মানগুলি আস্থা ব্যবধানের চেয়ে কম। স্বাভাবিক বন্টনের অনুমান প্রত্যাখ্যান করা হয়, যা প্রমাণ করে যে বিটিসির রিটার্ন রেটে স্বাভাবিক বন্টনের বৈশিষ্ট্য নেই এবং পরীক্ষামূলক গবেষণায় ঘন ফ্যাট লেজের বৈশিষ্ট্য রয়েছে।

১-৪. বাস্তবায়িত ও পর্যবেক্ষণকৃত অস্থিরতার তুলনা

আমরা পর্যবেক্ষণের জন্য square_log_return (logarithmic yield squared) এবং realized_variance (realized variance) একত্রিত করি।

[11] এঃ

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

আউট[11]:

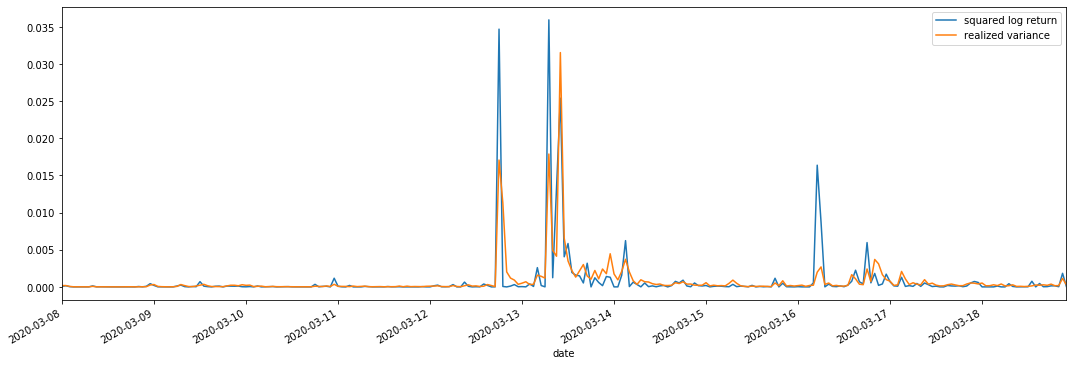
এটি দেখা যায় যে যখন উপলব্ধি করা বৈচিত্র্য পরিসীমা বড় হয়, রিটার্ন রেট পরিসরের অস্থিরতাও বড় হয় এবং উপলব্ধি করা রিটার্ন রেট মসৃণ হয়। উভয়ই সুস্পষ্ট সমষ্টিগত প্রভাবগুলি পর্যবেক্ষণ করা সহজ।

বিশুদ্ধভাবে তাত্ত্বিক দৃষ্টিকোণ থেকে, আরভি বাস্তব অস্থিরতার নিকটবর্তী, যখন অন্তঃদিবসের অস্থিরতা রাতারাতি ডেটাতে অন্তর্ভুক্ত হওয়ার কারণে স্বল্পমেয়াদী অস্থিরতা মসৃণ হয়, তাই পর্যবেক্ষণের দৃষ্টিকোণ থেকে, অন্তঃদিবসের অস্থিরতা স্টক মার্কেটের অস্থিরতার নিম্ন ফ্রিকোয়েন্সির জন্য আরও উপযুক্ত। উচ্চ ফ্রিকোয়েন্সি ট্রেডিং এবং বিটিসির 7 * 24 ঘন্টা বাজারের বৈশিষ্ট্যগুলি এটিকে বেঞ্চমার্ক অস্থিরতা নির্ধারণের জন্য আরভি ব্যবহার করতে আরও উপযুক্ত করে তোলে।

২. সময়ের ধারাবাহিকের মসৃণতা

যদি এটি একটি নন-স্টেশনারি সিরিজ হয়, তবে এটিকে প্রায় একটি স্টেশনারি সিরিজের সাথে সামঞ্জস্য করা দরকার। সাধারণ উপায় হ'ল পার্থক্য প্রক্রিয়াকরণ করা। তাত্ত্বিকভাবে, অনেকবারের পার্থক্যের পরে, নন-স্টেশনারি সিরিজটি একটি স্টেশনারি সিরিজের কাছাকাছি হতে পারে। যদি নমুনা সিরিজের কোভ্যারিয়েন্সি স্থিতিশীল হয় তবে এর পর্যবেক্ষণের প্রত্যাশা, বৈচিত্র্য এবং কোভ্যারিয়েন্সি সময়ের সাথে পরিবর্তন হবে না, যা ইঙ্গিত করে যে নমুনা সিরিজটি পরিসংখ্যান বিশ্লেষণে অনুমানের জন্য আরও সুবিধাজনক।

এখানে ইউনিট রুট পরীক্ষা, যথা এডিএফ পরীক্ষা, ব্যবহার করা হয়। ADF পরীক্ষাটি তাত্পর্য পর্যবেক্ষণের জন্য টি পরীক্ষা ব্যবহার করে। নীতিগতভাবে, যদি সিরিজটি সুস্পষ্ট প্রবণতা দেখায় না, তবে কেবল ধ্রুবক আইটেমগুলি ধরে রাখা হয়। যদি সিরিজের প্রবণতা থাকে তবে রিগ্রেশন সমীকরণটিতে ধ্রুবক আইটেম এবং সময় প্রবণতা আইটেম উভয়ই অন্তর্ভুক্ত করা উচিত। এছাড়াও, তথ্যের মানদণ্ডের ভিত্তিতে মূল্যায়নের জন্য এআইসি এবং বিআইসি মানদণ্ড ব্যবহার করা যেতে পারে। যদি সূত্রের প্রয়োজন হয় তবে এটি নিম্নরূপঃ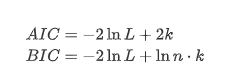

[8] এঃ

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

আউট[8]: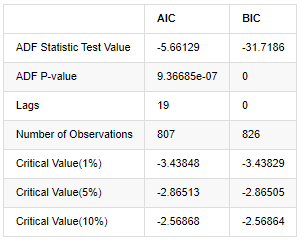

মূল অনুমানটি হ'ল সিরিজে কোনও ইউনিট রুট নেই, অর্থাৎ, বিকল্প অনুমানটি হ'ল সিরিজটি স্থির। পরীক্ষার পি মানটি 0.05% আত্মবিশ্বাসের স্তরের কাট-অফ মানের চেয়ে অনেক কম, মূল অনুমানটি প্রত্যাখ্যান করুন, সুতরাং লগ রেট অফ রিটার্ন একটি স্থির সিরিজ, পরিসংখ্যানগত সময় সিরিজ মডেল ব্যবহার করে মডেল করা যেতে পারে।

৩. মডেল সনাক্তকরণ এবং অর্ডার নির্ধারণ

গড় মান সমীকরণ প্রতিষ্ঠার জন্য, ত্রুটি পদটিতে স্বয়ংক্রিয় সম্পর্ক নেই তা নিশ্চিত করার জন্য ক্রমটিতে একটি স্বয়ংক্রিয় সম্পর্ক পরীক্ষা করা প্রয়োজন। প্রথমত, স্বয়ংক্রিয় সম্পর্ক ACF এবং আংশিক সম্পর্ক PACF নিম্নরূপ গ্রাফ করার চেষ্টা করুনঃ

[19] এঃ

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

আউট[19]:

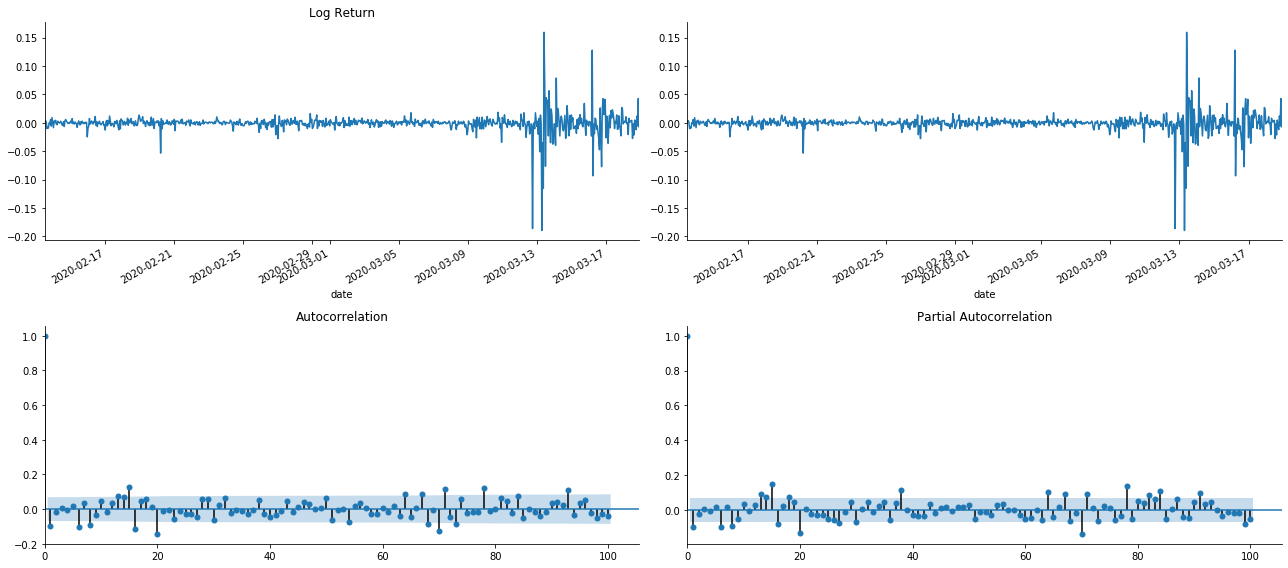
আপনি দেখতে পাচ্ছেন যে টর্নিং এর প্রভাব নিখুঁত। সেই মুহুর্তে, এই ছবিটি আমাকে অনুপ্রেরণা দিয়েছে। বাজারটি কি সত্যিই অবৈধ? যাচাই করার জন্য, আমরা রিটার্ন সিরিজে অটো-করেলেশন বিশ্লেষণ করব এবং মডেলের বিলম্বের আদেশ নির্ধারণ করব।

সাধারণভাবে ব্যবহৃত ক্যারেলেশন কোয়ালিফায়েন্টটি এটি এবং নিজের মধ্যে ক্যারেলেশন পরিমাপ করা, অর্থাৎ অতীতের একটি নির্দিষ্ট সময়ে r ((t) এবং r (t-l) এর মধ্যে ক্যারেলেশনঃ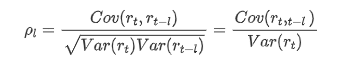

তারপরে আসুন একটি পরিমাণগত পরীক্ষা করি। মূল অনুমানটি হ'ল সমস্ত অটোকরেলেশন সহগগুলি 0 হয়, অর্থাৎ সিরিজে কোনও অটোকরেলেশন নেই। পরীক্ষার পরিসংখ্যান সূত্রটি নিম্নরূপ লেখা হয়েছেঃ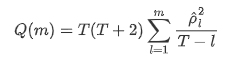

বিশ্লেষণের জন্য নিম্নরূপ দশটি অটো-কোরেলেশন কোঅফিসিয়েন্ট নেওয়া হয়েছিলঃ

[৯] এঃ

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

আউট[9]: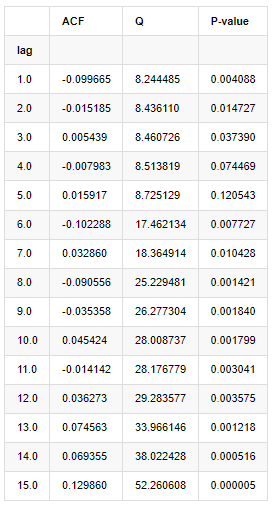

পরীক্ষার পরিসংখ্যান Q এবং P-value অনুযায়ী, আমরা দেখতে পাচ্ছি যে অটোকরেলেশন ফাংশন ACF ক্রমান্বয়ে 0 অর্ডার 0 এর পরে 0 হয়ে যায়। Q পরীক্ষার পরিসংখ্যানের P-মূল্যগুলি মূল অনুমানটি প্রত্যাখ্যান করার জন্য যথেষ্ট ছোট, তাই সিরিজে অটোকরেলেশন রয়েছে।

৪. এআরএমএ মডেলিং

এআর এবং এমএ মডেলগুলি বেশ সহজ। সহজভাবে বলতে গেলে, মার্কডাউন সূত্রগুলি লিখতে খুব ক্লান্ত। যদি আপনি আগ্রহী হন তবে দয়া করে সেগুলি নিজে পরীক্ষা করুন। এআর (অটোরেগ্রেশন) মডেলটি মূলত সময় সিরিজ মডেল করতে ব্যবহৃত হয়। যদি সিরিজটি এসিএফ পরীক্ষা পাস করে থাকে, অর্থাৎ, 1 এর ব্যবধানের সাথে অটোকরলেশন সহগটি উল্লেখযোগ্য, অর্থাৎ, সময়ে ডেটা সময়টি ভবিষ্যদ্বাণী করার জন্য দরকারী হতে পারে।

এমএ (মুভিং এভারেজ) মডেলটি বর্তমান পূর্বাভাস মানটি রৈখিকভাবে প্রকাশ করার জন্য অতীতের q সময়ের এলোমেলো হস্তক্ষেপ বা ত্রুটি পূর্বাভাস ব্যবহার করে।

তথ্যের গতিশীল কাঠামো সম্পূর্ণরূপে বর্ণনা করার জন্য, এআর বা এমএ মডেলগুলির আদেশ বাড়ানো প্রয়োজন, তবে এই ধরনের পরামিতিগুলি গণনাকে আরও জটিল করে তুলবে। অতএব, এই প্রক্রিয়াটি সহজ করার জন্য, একটি স্বয়ংক্রিয়ভাবে গতিশীল গড় (এআরএমএ) মডেল প্রস্তাব করা হয়।

যেহেতু মূল্যের সময় সিরিজগুলি সাধারণত স্থিতিশীল নয় এবং স্থিতিশীলতার উপর পার্থক্য পদ্ধতির অপ্টিমাইজেশান প্রভাবটি পূর্বে আলোচনা করা হয়েছে, তাই এআরআইএমএ (পি, ডি, কিউ) (সমাপ্তি অটোরেগ্রেসিভ চলমান গড়) মডেলটি বিদ্যমান মডেলগুলিকে সিরিজে প্রয়োগের ভিত্তিতে ডি-অর্ডার পার্থক্য প্রক্রিয়াকরণ যুক্ত করে। তবে, যেহেতু আমরা লগারিদম ব্যবহার করেছি, আমরা সরাসরি এআরএমএ (পি, কিউ) ব্যবহার করতে পারি।

সংক্ষেপে, এআরআইএমএ মডেল এবং এআরএমএ মডেল বিল্ডিং প্রক্রিয়ার মধ্যে একমাত্র পার্থক্য হ'ল স্থিতিশীলতা বিশ্লেষণের পরে যদি অস্থিতিশীল ফলাফলগুলি পাওয়া যায় তবে মডেলটি সরাসরি সিরিজের সাথে একটি বর্গক্ষেত্রীয় পার্থক্য করবে এবং তারপরে স্থিতিশীলতা পরীক্ষা সম্পাদন করবে এবং তারপরে সিরিজটি স্থিতিশীল না হওয়া পর্যন্ত p এবং q অর্ডার নির্ধারণ করবে। মডেলটি তৈরি এবং মূল্যায়ন করার পরে, পরবর্তী ভবিষ্যদ্বাণী করা হবে, পার্থক্যটি করার জন্য ফিরে যাওয়ার পদক্ষেপটি বাদ দেওয়া হবে। তবে, দ্বিতীয় আদেশের দামের পার্থক্য অর্থহীন, তাই এআরএমএ সেরা পছন্দ।

৪-১। অর্ডার নির্বাচন

এরপরে, আমরা তথ্যের মানদণ্ডের মাধ্যমে সরাসরি ক্রম নির্বাচন করতে পারি, এখানে আমরা এটি AIC এবং BIC এর তাপগতিবিদ্যা ডায়াগ্রামের সাথে চেষ্টা করি।

[১০] এঃ

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

আউট[10]: এআইসি সেরা পরামিতিঃ (0, 1, 1) বিআইসি সেরা প্যারামিটারঃ (0, 1, 1) HQIC সেরা প্যারামিটারঃ (0, 1, 1) সেরা প্যারাম নির্বাচিতঃ (0, 1, 1)

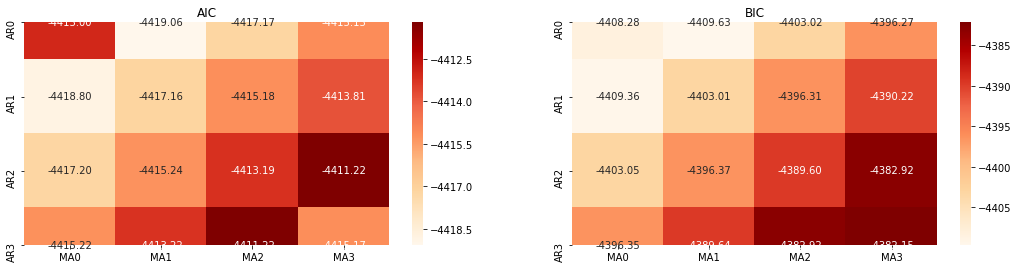
এটা স্পষ্ট যে লগারিদমিক মূল্যের জন্য সর্বোত্তম প্রথম-অর্ডার প্যারামিটার সংমিশ্রণটি (0,1,1), যা সহজ এবং সরল। লগ_রিটার্ন (লগারিদমিক রিটার্নের হার) একই অপারেশন সম্পাদন করে। এআইসি সর্বোত্তম মান (4,3) এবং বিআইসি সর্বোত্তম মান (0,1) । সুতরাং লগ_রিটার্ন (লগারিদমিক রিটার্নের হার) এর জন্য প্যারামিটারগুলির সর্বোত্তম সংমিশ্রণটি (0,1) ।

৪-২। এআরএমএ মডেলিং এবং মেলে

ত্রৈমাসিক সহগগুলি প্রয়োজন হয় না, কিন্তু SARIMAX বৈশিষ্ট্যগুলিতে সমৃদ্ধ, তাই মডেলিংয়ের জন্য এই মডেলটি বেছে নেওয়ার সিদ্ধান্ত নেওয়া হয়েছিল এবং ঘটনাক্রমে নিম্নরূপ একটি বর্ণনামূলক বিশ্লেষণ আঁকতে হবেঃ

[11] এঃ

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

আউট[11]: স্টেটস্পেস মডেলের ফলাফল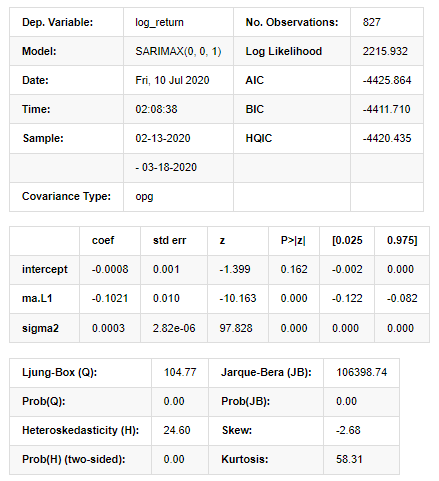

সতর্কতাঃ [1] গ্র্যাডিয়েন্টের বাইরের পণ্য ব্যবহার করে গণনা করা কোভ্যারিয়েন্স ম্যাট্রিক্স (জটিল-পদক্ষেপ) । [২৭] এঃ

model_results.plot_diagnostics(figsize=(18, 10));

আউট[২৭]:

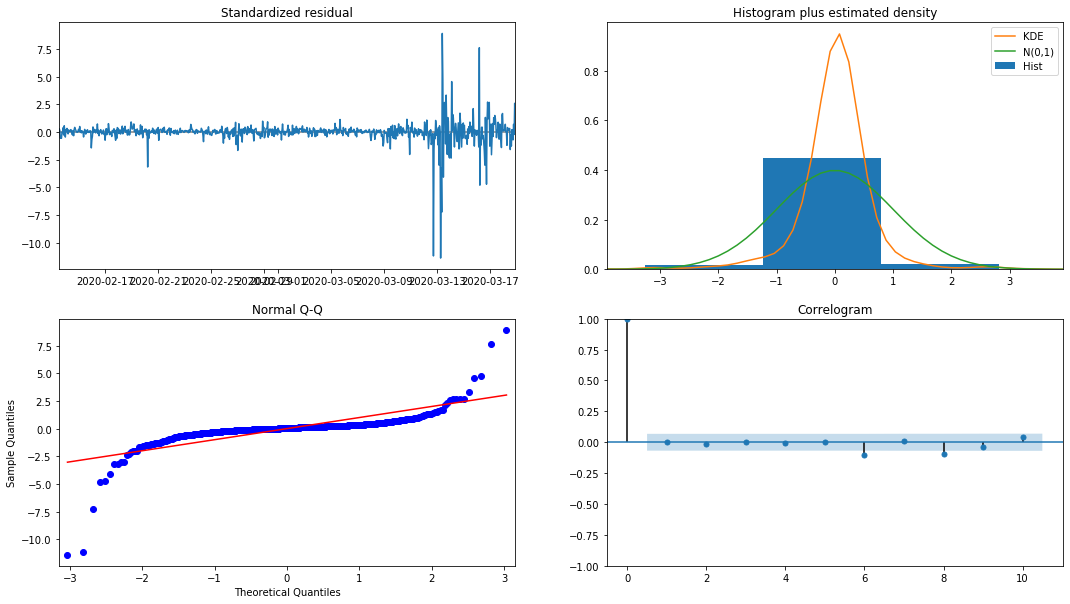
হিস্টোগ্রামের সম্ভাব্যতা ঘনত্ব KDE স্বাভাবিক বন্টন N (0,1) থেকে অনেক দূরে, যা নির্দেশ করে যে অবশিষ্টটি একটি স্বাভাবিক বন্টন নয়। QQ কোয়ান্টিল গ্রাফটিতে, স্ট্যান্ডার্ড স্বাভাবিক বন্টন থেকে নমুনা নেওয়া নমুনার অবশিষ্টগুলি সম্পূর্ণরূপে রৈখিক প্রবণতা অনুসরণ করে না, তাই এটি আবার নিশ্চিত হয় যে অবশিষ্টগুলি স্বাভাবিক বন্টন নয় এবং সাদা গোলমালের কাছাকাছি।

তারপরও, এই মডেলটি ব্যবহার করা যায় কিনা তা এখনও পরীক্ষা করা দরকার।

৪-৩। মডেল টেস্ট

অবশিষ্টের মিলন প্রভাব আদর্শ নয়, তাই আমরা এটিতে ডারবিন ওয়াটসন পরীক্ষাটি সম্পাদন করেছি। পরীক্ষার মূল অনুমানটি হ'ল ক্রমটির অটোকরেলেশন নেই এবং বিকল্প অনুমান ক্রম স্থির। এছাড়াও, যদি এলবি, জেবি এবং এইচ পরীক্ষার পি মানগুলি 0.05% আত্মবিশ্বাসের স্তরের সমালোচনামূলক মানের চেয়ে কম হয় তবে মূল অনুমানটি প্রত্যাখ্যান করা হবে।

[১২] এঃ

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

আউট[১২]: অবশিষ্টের পরীক্ষা heteroskedasticity (breakvar): stat=24.598, p=0.000

অবশিষ্টের পরীক্ষার স্বাভাবিকতা (জার্কেবেরা): stat=106398.739, p=0.000

অবশিষ্টের পরীক্ষার সিরিয়াল সম্পর্ক (ljungbox): stat=104.767, p=0.000

অবশিষ্টাংশের জন্য ডারবিন-ওয়াটসন পরীক্ষাঃ d=2.00 (দ্রষ্টব্যঃ ২ মানে কোনো সিরিয়াল ক্যারেলেশন নেই, ০=পোস, ৪=নেগেটিভ)

ইউনিট সার্কেলের বাইরে সমস্ত AR রুটের জন্য পরীক্ষা (>1): সত্য

ইউনিট সার্কেলের বাইরে সমস্ত এমএ রুটের জন্য পরীক্ষা (>1): সত্য

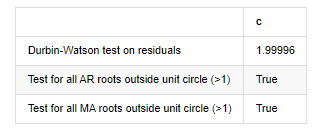
[13] এঃ

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

আউট[13]:

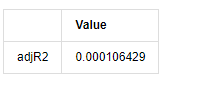
যদি ডারবিন ওয়াটসন পরীক্ষার পরিসংখ্যান 2 এর সমান হয়, তবে সিরিজের কোনও সম্পর্ক নেই এবং এর পরিসংখ্যানগত মানটি (0,4) এর মধ্যে বিতরণ করা হয়েছে তা নিশ্চিত করে। 0 এর কাছাকাছি হওয়ার অর্থ হ'ল ইতিবাচক সম্পর্ক উচ্চ, যখন 4 এর কাছাকাছি হওয়ার অর্থ হ'ল নেতিবাচক সম্পর্ক উচ্চ। এখানে এটি আনুমানিক 2 এর সমান। অন্যান্য পরীক্ষার পি মান যথেষ্ট ছোট, ইউনিট বৈশিষ্ট্যগত রুট ইউনিট বৃত্তের বাইরে, এবং পরিবর্তিত অ্যাজআর 2 এর মান যত বড় হবে তত ভাল হবে। পরিমাপের সামগ্রিক ফলাফল সন্তোষজনক বলে মনে হয় না।

[14] এঃ

model_results.params

আউট[14]: ইন্টারসেপ্ট -0.000817 ma.L1 -0.102102 সিগমা২ ০.০০০২৭৫ dtype: float64

সংক্ষেপে, এই অর্ডার সেটিং প্যারামিটারটি মূলত সময় সিরিজ মডেলিং এবং পরবর্তী অস্থিরতা মডেলিংয়ের প্রয়োজনীয়তা পূরণ করতে পারে তবে মেলে এমন প্রভাব রয়েছে। মডেল এক্সপ্রেশনটি নিম্নরূপঃ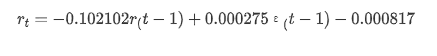

৪-৪। মডেল পূর্বাভাস

পরবর্তী, প্রশিক্ষিত মডেলটি সামনের দিকে মেলে। statsmodels মেলে এবং পূর্বাভাসের জন্য স্ট্যাটিক এবং গতিশীল বিকল্পগুলি সরবরাহ করে। পার্থক্যটি হ'ল পূর্বাভাসের পরবর্তী পদক্ষেপে পর্যবেক্ষণ মানটি ব্যবহৃত হয়, বা পূর্ববর্তী পদক্ষেপে উত্পন্ন পূর্বাভাসের মানটি পুনরাবৃত্তিভাবে ব্যবহৃত হয়। লগ_রিটার্নের পূর্বাভাসের প্রভাবগুলি নিম্নরূপঃ

[৩৭] এঃ

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

আউট[37]:

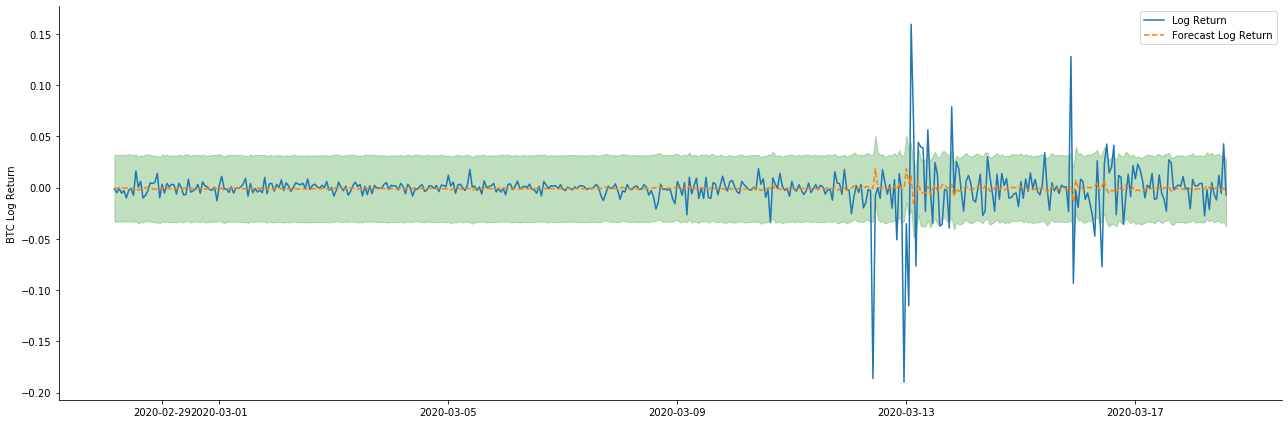
এটা দেখা যায় যে, নমুনার উপর স্ট্যাটিক মোডের ফিটিং এফেক্ট চমৎকার, নমুনা ডেটা প্রায় 95% কনফিডেন্স ইন্টারval দ্বারা আচ্ছাদিত হতে পারে, এবং গতিশীল মোড কিছুটা নিয়ন্ত্রণের বাইরে।

সুতরাং চলুন ডায়নামিক মোডে ডেটা মেলে প্রভাব তাকানঃ

[38] এঃ

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

আউট[38]:

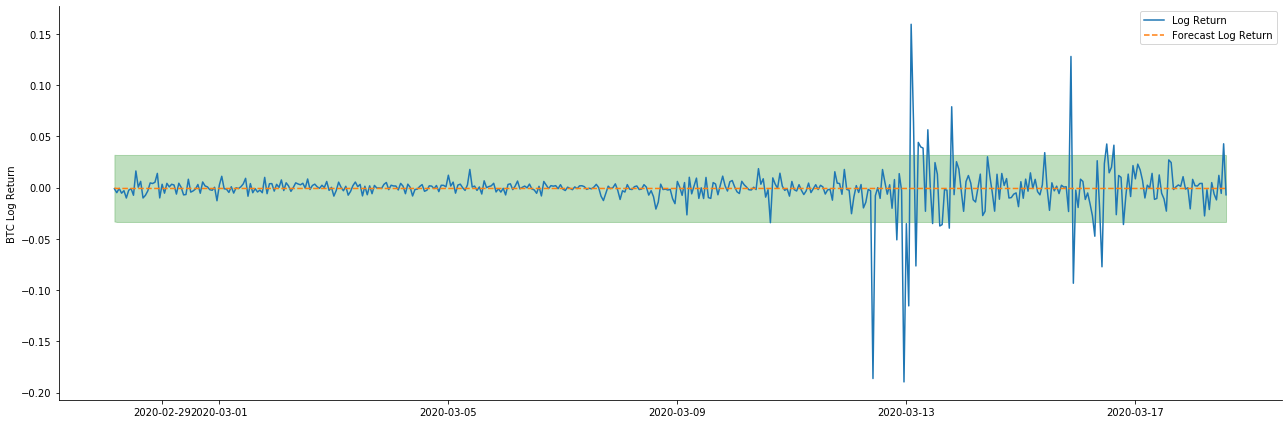
এটি দেখা যায় যে নমুনার উপর দুটি মডেলের ফিটিং প্রভাব দুর্দান্ত, এবং গড় মানটি প্রায় 95% নির্ভরযোগ্যতার ব্যবধান দ্বারা আচ্ছাদিত হতে পারে, তবে স্ট্যাটিক মডেলটি স্পষ্টতই আরও উপযুক্ত। এরপরে, আসুন নমুনার বাইরে 50 টি পদক্ষেপের পূর্বাভাস প্রভাবটি দেখুন, অর্থাৎ প্রথম 50 ঘন্টাঃ

[৪১] এঃ

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

আউট [41]:

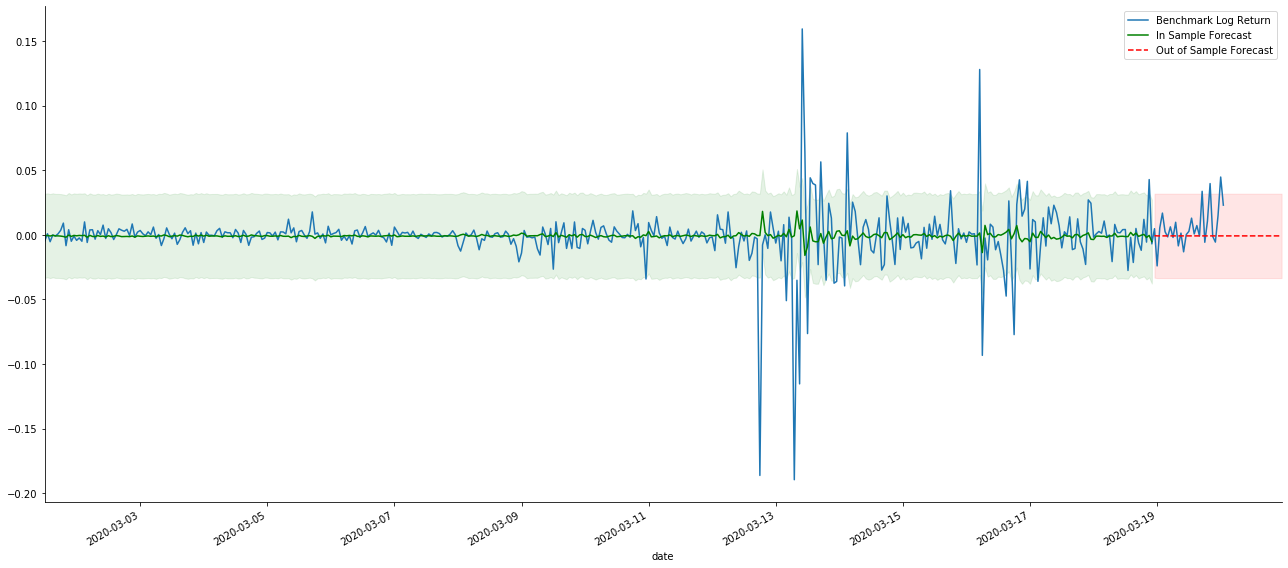
যেহেতু নমুনার মধ্যে ডেটাগুলির মিল একটি রোলিং ফরওয়ার্ড পূর্বাভাস, যখন নমুনার মধ্যে তথ্যের পরিমাণ পর্যাপ্ত হয়, তখন স্ট্যাটিক মডেলটি ওভার ম্যাচিংয়ের প্রবণ, যখন গতিশীল মডেলের নির্ভরযোগ্য নির্ভরশীল ভেরিয়েবলগুলির অভাব হয় এবং পুনরাবৃত্তির পরে প্রভাবটি আরও খারাপ হয়। নমুনার বাইরে ডেটা পূর্বাভাস দেওয়ার সময়, মডেলটি নমুনার মধ্যে গতিশীল মডেলের সমতুল্য, তাই দীর্ঘমেয়াদী পূর্বাভাসের ত্রুটি মেয়াদের নির্ভুলতা কম হতে বাধ্য।

যদি আমরা রিটার্ন রেট পূর্বাভাসকে log_price (লোগারিথমিক মূল্য) তে বিপরীত করি, তাহলে ম্যাচটি নিচের চিত্রটিতে দেখানো হয়েছেঃ

[42]-এঃ

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

আউট [42]:

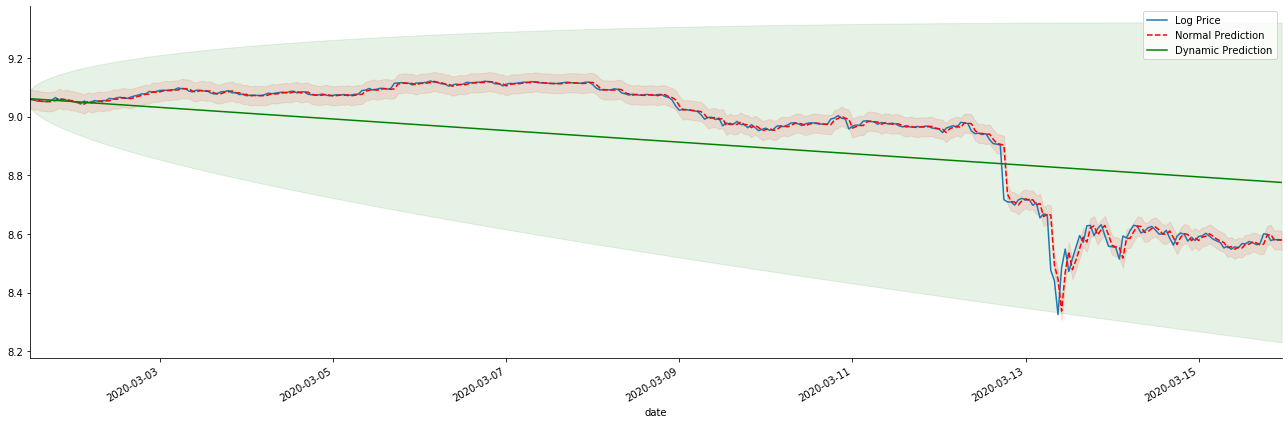
স্ট্যাটিক মডেলের মিলিত সুবিধা এবং দীর্ঘমেয়াদী পূর্বাভাসে গতিশীল মডেল এবং স্ট্যাটিক মডেলের মধ্যে চরম পার্থক্য দেখা সহজ। লাল বিন্দুযুক্ত লাইন এবং গোলাপী ব্যাপ্তি... আপনি বলতে পারবেন না যে এই মডেলের পূর্বাভাস ভুল। সর্বোপরি, এটি চলমান গড়ের প্রবণতা পুরোপুরি কভার করে, কিন্তু... এটি কি অর্থপূর্ণ?

প্রকৃতপক্ষে, এআরএমএ মডেলটি নিজেই ভুল নয়, কারণ সমস্যাটি মডেলটি নিজেই নয়, তবে জিনিসগুলির উদ্দেশ্যমূলক যুক্তি। পূর্ববর্তী এবং পরবর্তী পর্যবেক্ষণগুলির মধ্যে সম্পর্ক ভিত্তিতে কেবলমাত্র সময় সিরিজ মডেলটি প্রতিষ্ঠিত করা যায়। অতএব, সাদা গোলমাল সিরিজ মডেল করা অসম্ভব। অতএব, পূর্ববর্তী সমস্ত কাজ একটি সাহসী অনুমানের উপর ভিত্তি করে যে বিটিসির রিটার্ন রেট সিরিজ স্বাধীন এবং একইভাবে বিতরণ করা যায় না।

সাধারণভাবে, রিটার্ন রেট সিরিজগুলি মার্টিনগাল পার্থক্য সিরিজ, যার অর্থ হল যে রিটার্ন রেটটি অনির্দেশ্য, এবং সংশ্লিষ্ট বাজারের দুর্বল দক্ষতা অনুমানটি ধরে রাখে। আমরা অনুমান করেছি যে পৃথক নমুনার রিটার্ন রেটগুলির একটি নির্দিষ্ট ডিগ্রি অটোকরেলেশন রয়েছে এবং একই বিতরণ অনুমানটি প্রশিক্ষণের সেটে মেলে এমন মডেলটি প্রয়োগ করা, যাতে একটি সাধারণ এআরএমএ মডেল মেলে, যার একটি দুর্বল ভবিষ্যদ্বাণীমূলক প্রভাব থাকতে পারে।

যাইহোক, মেলে থাকা অবশিষ্ট ক্রমটিও একটি মার্টিনগাল পার্থক্য ক্রম। মার্টিনগাল পার্থক্য ক্রমটি স্বাধীন এবং একইভাবে বিতরণ করা নাও হতে পারে, তবে শর্তাধীন বৈচিত্র্য অতীত মানের উপর নির্ভর করতে পারে, তাই প্রথম শ্রেণীর অটো-সংযুক্তি চলে গেছে, তবে এখনও উচ্চতর অর্ডার অটো-সংযুক্তি রয়েছে, যা উদ্বায়ীতা মডেলিং এবং পর্যবেক্ষণের জন্য একটি গুরুত্বপূর্ণ পূর্বশর্ত।

যদি এই ধরনের যুক্তি সত্য হয়, তাহলে বিভিন্ন অস্থিরতা মডেল নির্মাণের ভিত্তিও সত্য। সুতরাং একটি রিটার্ন রেট সিরিজের জন্য, যদি একটি দুর্বল দক্ষ বাজার সন্তুষ্ট হয়, তবে গড় মানটি ভবিষ্যদ্বাণী করা কঠিন হতে হবে, তবে বৈচিত্র্যটি ভবিষ্যদ্বাণীযোগ্য। এবং মেলে ARMA একটি ন্যায্য মানের সময় সিরিজ বেঞ্চমার্ক সরবরাহ করে, তারপরে গুণমানটি অস্থিরতা ভবিষ্যদ্বাণীর গুণমানও নির্ধারণ করে।

পরিশেষে, আসুন কেবলমাত্র পূর্বাভাসের প্রভাবটি মূল্যায়ন করি। মূল্যায়ন বেঞ্চমার্ক হিসাবে ত্রুটি সহ, নমুনার অভ্যন্তরে এবং বাইরে সূচকগুলি নিম্নরূপঃ

[15] এঃ

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

আউট[15]: মূল গড় বর্গক্ষেত্র ত্রুটি (RMSE): 0.0184 মূল গড় বর্গক্ষেত্র ত্রুটি (RMSE): 0.0167 গড় পরম শতাংশ ত্রুটি (এমএপিই): ২.২৫ ই+০৩ গড় পরম শতাংশ ত্রুটি (এমএপিই): ৩৯৫

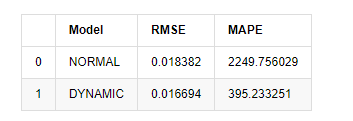
এটি দেখা যায় যে স্ট্যাটিক মডেলটি পূর্বাভাসিত মান এবং বাস্তব মানের মধ্যে ত্রুটি মিলের দিক থেকে গতিশীল মডেলের চেয়ে কিছুটা ভাল। এটি বিটকয়েনের লগারিদমিক রিটার্ন রেটের সাথে ভালভাবে মেলে, যা মূলত প্রত্যাশার সাথে সামঞ্জস্যপূর্ণ। গতিশীল পূর্বাভাসের আরও নির্ভুল পরিবর্তনশীল তথ্যের অভাব রয়েছে এবং ত্রুটিটি পুনরাবৃত্তির মাধ্যমেও প্রসারিত হয়, তাই পূর্বাভাস প্রভাবটি খারাপ। এমএপিই 100% এর বেশি, তাই উভয় মডেলের প্রকৃত মেলে মানের মান আদর্শ নয়।

[18] এঃ

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

আউট[18]:

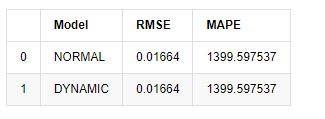
যেহেতু নমুনার বাইরে পরবর্তী ভবিষ্যদ্বাণী পূর্ববর্তী ধাপের ফলাফলের উপর নির্ভর করে, শুধুমাত্র গতিশীল মডেলটি কার্যকর। তবে, গতিশীল মডেলের দীর্ঘমেয়াদী ত্রুটি ত্রুটি সামগ্রিক মডেলের অপর্যাপ্ত ভবিষ্যদ্বাণী করার ক্ষমতা নিয়ে আসে, তাই পরবর্তী ধাপটি সর্বাধিক ভবিষ্যদ্বাণী করা হয়।

সংক্ষেপে, এআরএমএ মডেল স্ট্যাটিক মডেলটি বিটকয়েনের ইনট্রা স্যাম্পল রেট অফ রিটার্নের সাথে মেলে। রিটার্নের হারের স্বল্পমেয়াদী পূর্বাভাস কার্যকরভাবে আত্মবিশ্বাসের ব্যবধানটি কভার করতে পারে, তবে দীর্ঘমেয়াদী পূর্বাভাসটি খুব কঠিন, যা বাজারের দুর্বল কার্যকারিতা পূরণ করে। পরীক্ষার পরে, নমুনা ব্যবধানের মধ্যে রিটার্নের হার পরবর্তী অস্থিরতা পর্যবেক্ষণের ভিত্তি পূরণ করে।

৫. আর্ক প্রভাব

এআরসিএইচ মডেল প্রভাব শর্তাধীন heteroscedasticity ক্রম সিরিজ correlation হয়। মিশ্রণ পরীক্ষা Ljung বক্স ARCH প্রভাব আছে কিনা তা নির্ধারণ করার জন্য অবশিষ্ট বর্গক্ষেত্র সিরিজের correlation পরীক্ষা করতে ব্যবহৃত হয়। যদি ARCH প্রভাব পরীক্ষা পাস করা হয়, অর্থাৎ, সিরিজ heteroscedasticity আছে, গার্চ মডেলিং এর পরবর্তী ধাপ যৌথভাবে গড় সমীকরণ এবং উদ্বায়ীতা সমীকরণ অনুমান করা যেতে পারে। অন্যথায়, মডেল অপ্টিমাইজ করা এবং পুনরায় সমন্বয় করা প্রয়োজন, যেমন ডিফারেনশিয়াল প্রক্রিয়াকরণ বা পারস্পরিক সিরিজ।

আমরা এখানে কিছু ডেটা সেট এবং গ্লোবাল ভেরিয়েবল প্রস্তুত করছিঃ

[33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

আউট[33]:

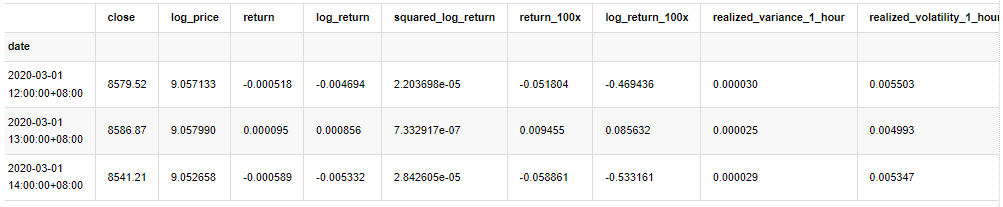
[22]-এঃ

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

আউট[22]: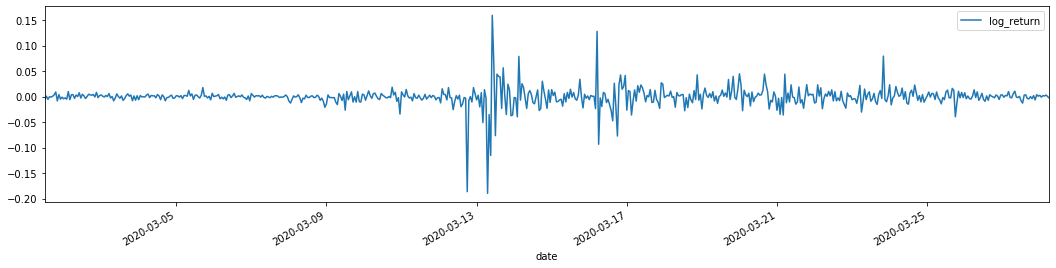

লোগারিদমিক রিটার্ন রেট উপরে দেখানো হয়েছে। পরবর্তী, আমাদের নমুনার ARCH প্রভাব পরীক্ষা করতে হবে। আমরা ARMA এর উপর ভিত্তি করে নমুনার মধ্যে অবশিষ্ট সিরিজ স্থাপন করি। কিছু সিরিজ এবং অবশিষ্ট এবং অবশিষ্টের বর্গাকার সিরিজ প্রথমে গণনা করা হয়ঃ

[২০] এঃ

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

আউট[20]:

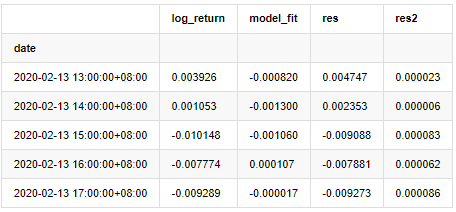
তারপরে নমুনার অবশিষ্ট সিরিজটি গ্রাফ করা হয়

[৬৯] এঃ

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

আউট[69]:

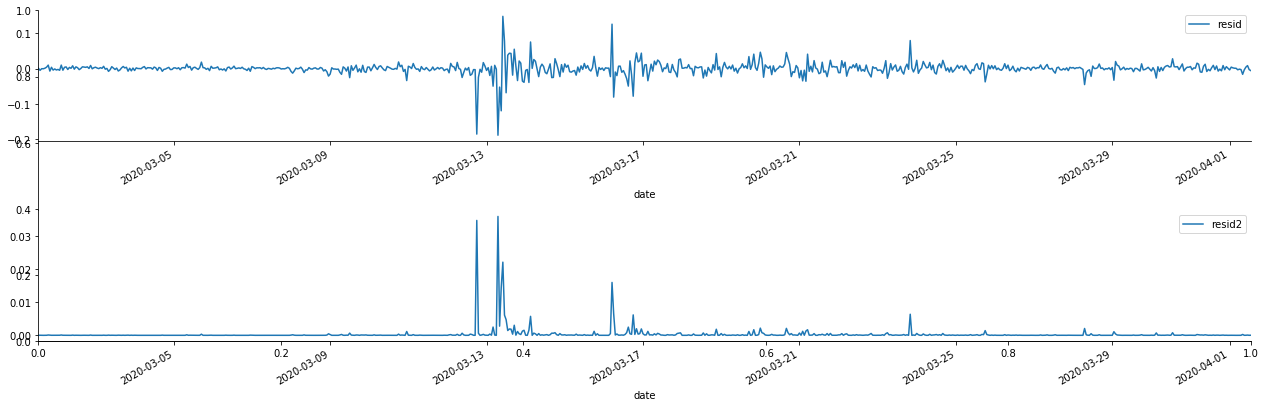
এটি দেখা যায় যে অবশিষ্ট সিরিজের সুস্পষ্ট সমষ্টিগত বৈশিষ্ট্য রয়েছে, এবং এটি প্রাথমিকভাবে বিচার করা যেতে পারে যে সিরিজের ARCH প্রভাব রয়েছে। ACF এছাড়াও বর্গক্ষেত্র অবশিষ্টগুলির স্বয়ংসম্পর্ক পরীক্ষা করার জন্য নেওয়া হয়, এবং ফলাফলগুলি নিম্নরূপ।

[৭০] এঃ

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

আউট[70]:

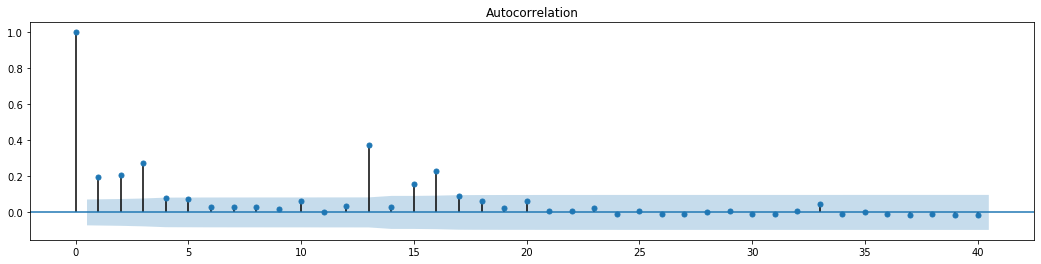
সিরিজ মিশ্রণ পরীক্ষার জন্য প্রাথমিক অনুমানটি হ'ল সিরিজের কোনও সম্পর্ক নেই। দেখা যায় যে প্রথম ২০ টি অর্ডারের ডেটার সংশ্লিষ্ট পি মানগুলি 0.05% আত্মবিশ্বাসের স্তরের সমালোচনামূলক মানের চেয়ে কম। অতএব, মূল অনুমানটি প্রত্যাখ্যান করা হয়, অর্থাৎ সিরিজের অবশিষ্টটির এআরসিএইচ প্রভাব রয়েছে। অবশিষ্ট সিরিজের heteroscedasticity ফিট করতে এবং আরও উদ্বায়ীতা পূর্বাভাস দেওয়ার জন্য ARCH টাইপ মডেলের মাধ্যমে বৈচিত্র্য মডেলটি প্রতিষ্ঠিত করা যেতে পারে।

৬. গার্চ মডেলিং

গার্চ মডেলিং করার আগে, আমাদের সিরিজের মোটা লেজ অংশটি মোকাবেলা করতে হবে। কারণ অনুমানটিতে সিরিজের ত্রুটি পদটি স্বাভাবিক বন্টন বা টি বন্টনের সাথে সামঞ্জস্যপূর্ণ হওয়া দরকার, এবং আমরা পূর্বে যাচাই করেছি যে ফলন সিরিজের একটি মোটা লেজ বন্টন রয়েছে, তাই আমাদের এই অংশটি বর্ণনা এবং পরিপূরক করতে হবে।

গার্চ মডেলিংয়ে, ত্রুটি আইটেমটি স্বাভাবিক বন্টন, টি-বন্টন, জিইডি (সাধারণ ত্রুটি বন্টন) বন্টন এবং স্কিউড স্টুডেন্টস টি-বন্টনের বিকল্পগুলি সরবরাহ করে। এআইসি মানদণ্ড অনুসারে, আমরা সমস্ত বিকল্পের ফলাফলগুলি তুলনা করতে এবং জি এর সেরা মেলে মেলে ডিগ্রি পেতে গণনা যৌথ রিগ্রেশন অনুমান ব্যবহার করি।

সম্পর্কিত

আরো