ডেটা-চালিত প্রযুক্তির উপর ভিত্তি করে জোড়া বাণিজ্য
লেখক:এফএমজেড-লিডিয়া, সৃষ্টিঃ ২০২৩-০১-০৫ ০৯ঃ১০ঃ২৫, আপডেটঃ ২০২৪-১২-১৯ ০০ঃ২৭ঃ১০
ডেটা-চালিত প্রযুক্তির উপর ভিত্তি করে জোড়া বাণিজ্য
জোড়া ট্রেডিং হল গাণিতিক বিশ্লেষণের উপর ভিত্তি করে ট্রেডিং কৌশল তৈরির একটি ভাল উদাহরণ। এই নিবন্ধে, আমরা দেখাব কিভাবে জোড়া ট্রেডিং কৌশল তৈরি এবং স্বয়ংক্রিয় করতে ডেটা ব্যবহার করতে হয়।
মৌলিক নীতি
ধরুন আপনার কাছে বিনিয়োগের লক্ষ্য X এবং Y এর একটি জোড়া রয়েছে যার কিছু সম্ভাব্য সংযোগ রয়েছে। উদাহরণস্বরূপ, দুটি সংস্থা একই পণ্য উত্পাদন করে, যেমন পেপসি কোলা এবং কোকা কোলা। আপনি চান যে সময়ের সাথে সাথে দামের অনুপাত বা বেস স্প্রেড (যা দামের পার্থক্য নামেও পরিচিত) উভয়ই অপরিবর্তিত থাকে। তবে, সরবরাহ এবং চাহিদার অস্থায়ী পরিবর্তনগুলির কারণে, যেমন বিনিয়োগের লক্ষ্যের একটি বড় কেনা / বিক্রয় আদেশ এবং একটি সংস্থার গুরুত্বপূর্ণ খবরের প্রতিক্রিয়া, দুটি জোড়ার মধ্যে দামের পার্থক্য সময়ে সময়ে আলাদা হতে পারে। এই ক্ষেত্রে, একটি বিনিয়োগের বস্তু আপেক্ষিকভাবে অন্যটি নেমে যায়। আপনি যদি এই মতবিরোধের সাথে স্বাভাবিক অবস্থায় ফিরে আসতে চান তবে আপনি সর্বত্র ট্রেডিংয়ের সুযোগ (বা সালিশের সুযোগ) খুঁজে পেতে পারেন। এই ধরনের সালিশের সুযোগগুলি ডিজিটাল মুদ্রা বা দেশীয় পণ্যের ফিউচার বাজারে পাওয়া যেতে পারে, যেমন বিটিসি এবং একটি সংস্থার গুরুত্বপূর্ণ খবরের মধ্যে সম্পর্ক; নিরাপদ আশ্রয়স্থল, সয়া মল এবং সয়া তেল সম্পদের মধ্যে ফ্যুচারের জাতের মধ্যে সম্পর্ক।
যখন একটি অস্থায়ী মূল্য পার্থক্য থাকে, আপনি চমৎকার কর্মক্ষমতা সঙ্গে বিনিয়োগ বস্তু বিক্রি করবে (উর্ধ্বগামী বিনিয়োগ বস্তু) এবং খারাপ কর্মক্ষমতা সঙ্গে বিনিয়োগ বস্তু কিনতে (হ্রাস বিনিয়োগ বস্তু) । আপনি নিশ্চিত যে দুই বিনিয়োগ বস্তু মধ্যে সুদের মার্জিন অবশেষে দুর্দান্ত কর্মক্ষমতা সঙ্গে বিনিয়োগ বস্তু পতন বা খারাপ কর্মক্ষমতা সঙ্গে বিনিয়োগ বস্তু উত্থান, অথবা উভয় মাধ্যমে পড়া হবে। আপনার লেনদেন এই সব অনুরূপ পরিস্থিতিতে অর্থ উপার্জন করবে। যদি বিনিয়োগ বস্তু তাদের মধ্যে মূল্য পার্থক্য পরিবর্তন না করে একসাথে আপ বা ডাউন সরানো, আপনি অর্থ উপার্জন বা হারান হবে না।
সুতরাং, জোড়া ট্রেডিং একটি বাজার নিরপেক্ষ ট্রেডিং কৌশল, যা ব্যবসায়ীদের প্রায় কোনও বাজার অবস্থার থেকে লাভ করতে সক্ষম করেঃ আপ ট্রেন্ড, ডাউন ট্রেন্ড বা অনুভূমিক একীকরণ।
ধারণাটি ব্যাখ্যা করুনঃ দুটি অনুমানিত বিনিয়োগের লক্ষ্য
- এফএমজেড কোয়ান্ট প্ল্যাটফর্মে আমাদের গবেষণা পরিবেশ তৈরি করুন
প্রথমত, মসৃণভাবে কাজ করার জন্য, আমাদের আমাদের গবেষণা পরিবেশ তৈরি করতে হবে। এই নিবন্ধে, আমরা আমাদের গবেষণা পরিবেশ তৈরি করতে FMZ কোয়ান্ট প্ল্যাটফর্ম (FMZ.COM) ব্যবহার করি, মূলত সুবিধাজনক এবং দ্রুত এপিআই ইন্টারফেস এবং এই প্ল্যাটফর্মের ভাল প্যাকেজড ডকার সিস্টেমটি ব্যবহার করার জন্য।
FMZ Quant প্ল্যাটফর্মের আনুষ্ঠানিক নামে এই ডকার সিস্টেমকে ডকার সিস্টেম বলা হয়।
দয়া করে আমার আগের নিবন্ধটি দেখুন কিভাবে একটি ডকার এবং রোবট স্থাপন করবেনঃhttps://www.fmz.com/bbs-topic/9864.
যারা নিজের ক্লাউড কম্পিউটিং সার্ভার ক্রয় করতে চান তারা এই নিবন্ধটি দেখতে পারেনঃhttps://www.fmz.com/digest-topic/5711.
ক্লাউড কম্পিউটিং সার্ভার এবং ডকার সিস্টেম সফলভাবে স্থাপন করার পর, পরবর্তী আমরা পাইথন বর্তমান বৃহত্তম শিল্পকর্ম ইনস্টল করা হবেঃ Anaconda
এই নিবন্ধে প্রয়োজনীয় সমস্ত প্রাসঙ্গিক প্রোগ্রাম পরিবেশ (নির্ভরতা লাইব্রেরি, সংস্করণ পরিচালনা ইত্যাদি) বাস্তবায়ন করার জন্য, সবচেয়ে সহজ উপায় হ'ল অ্যানাকোন্ডা ব্যবহার করা। এটি একটি প্যাকেজড পাইথন ডেটা সায়েন্স বাস্তুতন্ত্র এবং নির্ভরতা লাইব্রেরি ম্যানেজার।
Anaconda এর ইনস্টলেশন পদ্ধতির জন্য, অনুগ্রহ করে Anaconda এর অফিসিয়াল গাইড দেখুনঃhttps://www.anaconda.com/distribution/.
এই নিবন্ধটি পাইথন বৈজ্ঞানিক কম্পিউটিংয়ের দুটি জনপ্রিয় এবং গুরুত্বপূর্ণ লাইব্রেরি নম্পি এবং পান্ডা ব্যবহার করবে।
উপরের মৌলিক কাজটি আমার পূর্ববর্তী নিবন্ধগুলিতেও উল্লেখ করতে পারে, যা অ্যানাকোন্ডা পরিবেশ এবং নম্পি এবং পান্ডা লাইব্রেরিগুলি কীভাবে সেট আপ করবেন তা পরিচয় করিয়ে দেয়। বিস্তারিত জানার জন্য, দয়া করে পড়ুনঃhttps://www.fmz.com/bbs-topic/9863.
এরপরে, আসুন
import numpy as np
import pandas as pd
import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)
import matplotlib.pyplot as plt
হ্যাঁ, আমরা পাইথনে একটি খুব বিখ্যাত চার্ট লাইব্রেরি ম্যাটপ্লটলিবও ব্যবহার করব।
আসুন একটি অনুমানিত বিনিয়োগের লক্ষ্য X তৈরি করি, এবং স্বাভাবিক বন্টনের মাধ্যমে তার দৈনিক রিটার্ন সিমুলেট করি এবং প্লট করি। তারপর আমরা দৈনিক X মান পেতে একটি সমষ্টিগত যোগফল সম্পাদন করি।
# Generate daily returns
Xreturns = np.random.normal(0, 1, 100)
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
Xreturns), name='X')
+ 50
X.plot(figsize=(15,7))
plt.show()
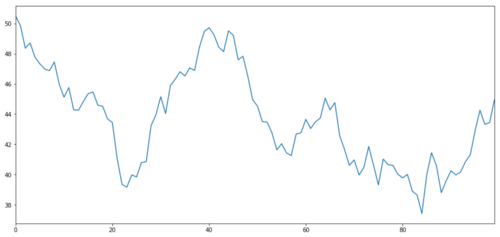
ইনভেস্টমেন্ট অবজেক্টের এক্সকে একটি স্বাভাবিক বন্টনের মাধ্যমে তার দৈনিক রিটার্নের প্লট করার জন্য সিমুলেট করা হয়
এখন আমরা Y উৎপন্ন করি, যা X এর সাথে দৃঢ়ভাবে সংহত, তাই Y এর দাম X এর পরিবর্তনের সাথে খুব অনুরূপ হওয়া উচিত। আমরা X নিয়ে এটি মডেল করি, এটিকে উপরে নিয়ে যাই এবং স্বাভাবিক বন্টন থেকে বের করা কিছু এলোমেলো শব্দ যোগ করি।
noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()
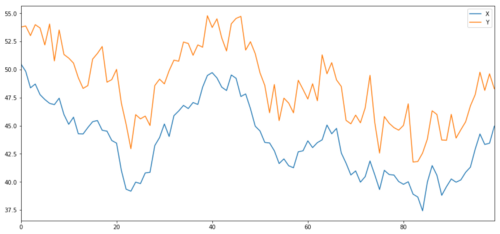
সমন্বয় বিনিয়োগের বস্তুর এক্স এবং ওয়াই
সমন্বয়
কোইন্টিগ্রেশন ক্যারেলেশনের অনুরূপ, যার অর্থ হল যে দুটি ডেটা সিরিজের মধ্যে অনুপাত গড় মানের কাছাকাছি পরিবর্তিত হবে। Y এবং X সিরিজগুলি নিম্নরূপঃ
Y =
যেখানে
দুইটি টাইম সিরিজের মধ্যে ট্রেডিংয়ের জন্য, সময়ের সাথে সাথে অনুপাতের প্রত্যাশিত মানটি গড় মানের সাথে একত্রিত হওয়া উচিত, অর্থাৎ, এগুলিকে একীভূত করা উচিত। আমরা উপরে যে টাইম সিরিজটি তৈরি করেছি তা একীভূত। আমরা এখন তাদের মধ্যে অনুপাতটি গ্রাফ করব যাতে আমরা দেখতে পারি এটি কেমন দেখাচ্ছে।
(Y/X).plot(figsize=(15,7))
plt.axhline((Y/X).mean(), color='red', linestyle='--')
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()
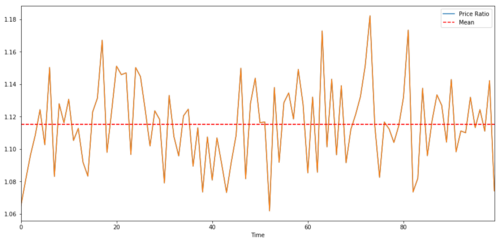
দুটি সমন্বিত বিনিয়োগের লক্ষ্য মূল্যের মধ্যে অনুপাত এবং গড় মূল্য
সমন্বয় পরীক্ষা
একটি সুবিধাজনক পরীক্ষার পদ্ধতি হল statsmodels.tsa.stattools ব্যবহার করা। আমরা একটি খুব কম p মান দেখতে হবে, কারণ আমরা কৃত্রিমভাবে দুটি ডেটা সিরিজ তৈরি করেছি যা যতটা সম্ভব সমন্বিত।
# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue
ফলাফল হল: 1.81864477307e-17
দ্রষ্টব্যঃ সংশ্লিষ্টতা এবং সমন্বয়
সম্পর্ক এবং সমন্বয়, যদিও তত্ত্বগতভাবে অনুরূপ, একই নয়। আসুন প্রাসঙ্গিক কিন্তু সমন্বিত নয় ডেটা সিরিজের উদাহরণ দেখুন এবং বিপরীতভাবে। প্রথমে, আসুন আমরা সবেমাত্র উত্পন্ন সিরিজের সম্পর্ক পরীক্ষা করি।
X.corr(Y)
ফলাফলঃ ০.৯৫১
যেমনটি আমরা আশা করেছিলাম, এটি খুব বেশি। কিন্তু দুটি সম্পর্কিত কিন্তু সমন্বিত নয় এমন সিরিজ সম্পর্কে কী? একটি সহজ উদাহরণ হল দুটি বিচ্যুত তথ্যের একটি সিরিজ।
ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)
s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')
pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)
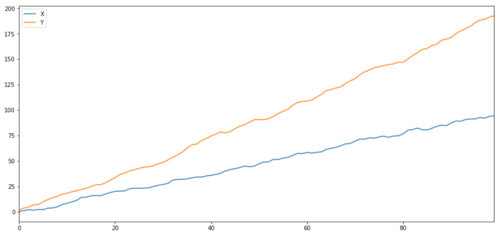
দুটি সম্পর্কিত সিরিজ (একসাথে সংহত নয়)
ক্যারলেশন কোয়ালিফায়ারঃ ০.৯৯৮ সমন্বয় পরীক্ষার পি মানঃ 0.258
সম্পর্কহীন সমন্বয়ের সহজ উদাহরণ হ'ল স্বাভাবিক বন্টন ক্রম এবং বর্গাকার তরঙ্গ।
Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)
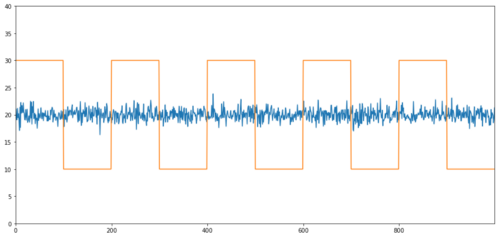
সম্পর্কঃ ০.০০৭৫৪৬ সমন্বয় পরীক্ষার পি মানঃ ০.০
সম্পর্ক খুবই কম, কিন্তু p মান নিখুঁত সমন্বয় দেখায়!
কিভাবে জোড়া ট্রেডিং পরিচালনা করবেন?
যেহেতু দুটি সমন্বিত সময় সিরিজ (যেমন উপরে এক্স এবং ওয়াই) একে অপরের মুখোমুখি এবং একে অপরের থেকে বিচ্যুত হয়, কখনও কখনও বেস স্প্রেডগুলি উচ্চ বা কম হয়। আমরা একটি বিনিয়োগ বস্তু কিনে অন্যটি বিক্রি করে জোড়া ট্রেডিং পরিচালনা করি। এইভাবে, যদি দুটি বিনিয়োগ লক্ষ্য একসাথে পড়ে বা বেড়ে যায় তবে আমরা অর্থ উপার্জন করব না বা অর্থ হারাব না, অর্থাৎ আমরা বাজারে নিরপেক্ষ।
উপরের দিকে ফিরে, Y =
লং রেসিওতে যাওয়া: যখন রেসিও
খুবই ছোট হয় এবং আমরা আশা করি এটি বৃদ্ধি পাবে। উপরের উদাহরণে, আমরা লং Y এবং শর্ট X দিয়ে পজিশনটি খুলি। শর্ট রেসিওঃ এটি যখন অনুপাত
খুব বড় হয় এবং আমরা এটি হ্রাস করার আশা করি। উপরের উদাহরণে, আমরা শর্ট Y এবং দীর্ঘ X দিয়ে অবস্থানটি খুলি।
অনুগ্রহ করে মনে রাখবেন যে আমাদের সবসময়
যদি ট্রেডিং অবজেক্টের এক্স এবং ওয়াই একে অপরের তুলনায় সরে যায়, তাহলে আমরা অর্থ উপার্জন করব অথবা অর্থ হারাব।
অনুরূপ আচরণ সঙ্গে ট্রেডিং বস্তু খুঁজে পেতে তথ্য ব্যবহার করুন
এটি করার সর্বোত্তম উপায় হ'ল আপনি যে ট্রেডিং সাবজেক্টটি সন্দেহ করছেন তা থেকে শুরু করে একটি পরিসংখ্যানগত পরীক্ষা সম্পাদন করা। আপনি যদি সমস্ত ট্রেডিং জোড়ার উপর পরিসংখ্যানগত পরীক্ষা পরিচালনা করেন তবে আপনিএকাধিক তুলনা পক্ষপাত.
একাধিক তুলনা পক্ষপাতঅনেকগুলি পরীক্ষা চালানোর সময় গুরুত্বপূর্ণ পি মানগুলি ভুলভাবে উত্পন্ন হওয়ার সম্ভাবনা বৃদ্ধি করে, কারণ আমাদের প্রচুর সংখ্যক পরীক্ষা চালাতে হবে। যদি আমরা এলোমেলো ডেটাতে 100 টি পরীক্ষা চালাই তবে আমাদের 0.05 এর নীচে 5 পি মান দেখতে হবে। যদি আপনি কো-ইন্টিগ্রেশনের জন্য n ট্রেডিং লক্ষ্যগুলি তুলনা করতে চান তবে আপনি n (n-1) / 2 তুলনা করবেন এবং আপনি অনেকগুলি ভুল পি মান দেখতে পাবেন, যা আপনার পরীক্ষার নমুনাগুলির বৃদ্ধিতে বৃদ্ধি পাবে। এই পরিস্থিতি এড়াতে, কয়েকটি ট্রেডিং জোড়া নির্বাচন করুন এবং আপনার কাছে নির্ধারণ করার কারণ রয়েছে যে তারা কো-ইন্টিগ্রেশন হতে পারে এবং তারপরে সেগুলি আলাদাভাবে পরীক্ষা করুন। এটি আপনার পরীক্ষার নমুনাগুলির বৃদ্ধিতে অনেকগুলি ভুল পি মান দেখতে পাবে।একাধিক তুলনা পক্ষপাত.
সুতরাং, আসুন আমরা কিছু ট্রেডিং টার্গেট খুঁজে বের করার চেষ্টা করি যা কো-ইন্টিগ্রেশন দেখায়। এসএন্ডপি 500 সূচকে বড় মার্কিন প্রযুক্তি স্টকগুলির একটি ঝুড়ি উদাহরণ হিসাবে নেওয়া যাক। এই ট্রেডিং টার্গেটগুলি অনুরূপ বাজার বিভাগে কাজ করে এবং কো-ইন্টিগ্রেশন দাম রয়েছে। আমরা ট্রেডিং অবজেক্টগুলির তালিকা স্ক্যান করি এবং সমস্ত জোড়ার মধ্যে কো-ইন্টিগ্রেশন পরীক্ষা করি।
রিটার্ন করা কো-ইন্টিগ্রেশন টেস্ট স্কোর ম্যাট্রিক্স, পি-ভ্যালু ম্যাট্রিক্স এবং সমস্ত জোড়া যার পি-ভ্যালু ০.০৫ এর কম।এই পদ্ধতিতে একাধিক তুলনা পক্ষপাতের প্রবণতা আছে, তাই আসলে, তারা একটি দ্বিতীয় যাচাইকরণ পরিচালনা করতে হবে।এই প্রবন্ধে, আমাদের ব্যাখ্যা সহজ করার জন্য, আমরা উদাহরণে এই পয়েন্টটি উপেক্ষা করার সিদ্ধান্ত নিয়েছি।
def find_cointegrated_pairs(data):
n = data.shape[1]
score_matrix = np.zeros((n, n))
pvalue_matrix = np.ones((n, n))
keys = data.keys()
pairs = []
for i in range(n):
for j in range(i+1, n):
S1 = data[keys[i]]
S2 = data[keys[j]]
result = coint(S1, S2)
score = result[0]
pvalue = result[1]
score_matrix[i, j] = score
pvalue_matrix[i, j] = pvalue
if pvalue < 0.02:
pairs.append((keys[i], keys[j]))
return score_matrix, pvalue_matrix, pairs
দ্রষ্টব্যঃ আমরা বাজারের বেঞ্চমার্ক (এসপিএক্স) তথ্য অন্তর্ভুক্ত করেছি - বাজার অনেক ট্রেডিং অবজেক্টের প্রবাহ চালিত করেছে। সাধারণত আপনি দুটি ট্রেডিং অবজেক্ট খুঁজে পেতে পারেন যা একত্রিত বলে মনে হয়; কিন্তু আসলে, তারা একে অপরের সাথে একত্রিত হয় না, তবে বাজারের সাথে। এটিকে বিভ্রান্তিকর পরিবর্তনশীল বলা হয়। আপনি যে কোনও সম্পর্কের মধ্যে বাজার অংশগ্রহণ পরীক্ষা করা গুরুত্বপূর্ণ।
from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
dataSetId=dataSetId,
instrumentIds=instrumentIds,
startDateStr=startDateStr,
endDateStr=endDateStr,
event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

এখন আমাদের পদ্ধতি ব্যবহার করে সমন্বিত ট্রেডিং জোড়া খুঁজে বের করার চেষ্টা করা যাক।
# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds,
yticklabels=instrumentIds, cmap=’RdYlGn_r’,
mask = (pvalues >= 0.98))
plt.show()
print pairs
[('ADBE', 'MSFT')]
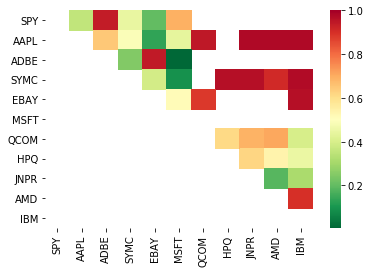
দেখে মনে হচ্ছে
S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()
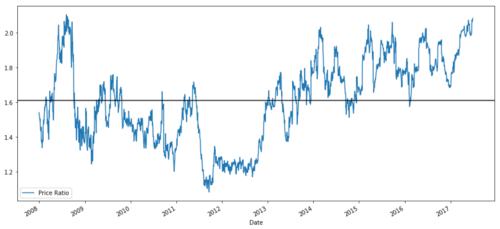
২০০৮ থেকে ২০১৭ সাল পর্যন্ত MSFT এবং ADBE এর মধ্যে মূল্য অনুপাতের চার্ট
এই অনুপাতটি একটি স্থিতিশীল গড়ের মতো দেখাচ্ছে। পরম অনুপাতগুলি পরিসংখ্যানগতভাবে দরকারী নয়। আমাদের সংকেতগুলিকে জেড স্কোর হিসাবে আচরণ করে স্ট্যান্ডার্ডাইজ করা আরও সহায়ক। জেড স্কোরটি সংজ্ঞায়িত করা হয়ঃ
Z স্কোর (মান) = (মান
সতর্কতা
প্রকৃতপক্ষে, আমরা সাধারণত তথ্যগুলি স্বাভাবিকভাবে বিতরণ করা হয় এই ধারণাটি দিয়ে ডেটা প্রসারিত করার চেষ্টা করি। তবে, অনেক আর্থিক তথ্য স্বাভাবিকভাবে বিতরণ করা হয় না, তাই পরিসংখ্যান তৈরি করার সময় আমাদের খুব সতর্ক থাকতে হবে যে কেবল স্বাভাবিকতা বা কোনও নির্দিষ্ট বিতরণ অনুমান না করা উচিত। অনুপাতের সত্যিকারের বিতরণ একটি ফ্যাট-tail প্রভাব থাকতে পারে, এবং যেসব তথ্য চরম হতে থাকে সেগুলি আমাদের মডেলকে বিভ্রান্ত করবে এবং বিশাল ক্ষতির দিকে পরিচালিত করবে।
def zscore(series):
return (series - series.mean()) / np.std(series)
zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()
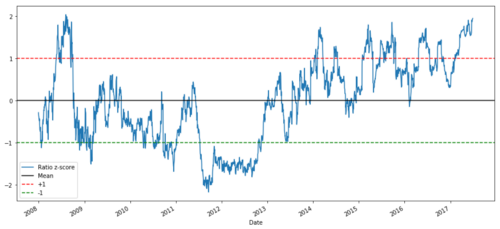
২০০৮ থেকে ২০১৭ সাল পর্যন্ত MSFT এবং ADBE এর মধ্যে Z মূল্য অনুপাত
এখন গড় মানের কাছাকাছি অনুপাতের গতিবিধি পর্যবেক্ষণ করা সহজ, কিন্তু মাঝারি মান থেকে মাঝে মাঝে বড় পার্থক্য থাকা সহজ। আমরা এর সুবিধা নিতে পারি।
এখন যেহেতু আমরা জোড়া ট্রেডিং কৌশল মৌলিক জ্ঞান নিয়ে আলোচনা করেছি, এবং ঐতিহাসিক মূল্যের উপর ভিত্তি করে যৌথ সংহতকরণের বিষয় নির্ধারণ করেছি, আসুন একটি ট্রেডিং সংকেত বিকাশ করার চেষ্টা করি। প্রথমত, আসুন ডেটা প্রযুক্তি ব্যবহার করে ট্রেডিং সংকেত বিকাশের পদক্ষেপগুলি পর্যালোচনা করিঃ
নির্ভরযোগ্য তথ্য সংগ্রহ এবং তথ্য পরিষ্কার করা;
ট্রেডিং সিগন্যাল/লজিক চিহ্নিত করার জন্য ডেটা থেকে ফাংশন তৈরি করা।
ফাংশনগুলি চলমান গড় বা মূল্যের ডেটা হতে পারে, আরও জটিল সংকেতগুলির সম্পর্ক বা অনুপাত - নতুন ফাংশন তৈরি করতে এগুলি একত্রিত করুন;
এই ফাংশনগুলি ব্যবহার করে ট্রেডিং সিগন্যাল তৈরি করুন, অর্থাৎ কোন সিগন্যালগুলি ক্রয়, বিক্রয় বা শর্ট পজিশনের দিকে নজর রাখবে।
সৌভাগ্যবশত, আমরা FMZ Quant প্ল্যাটফর্ম (fmz.com) আছে, যা আমাদের জন্য উপরের চারটি দিক সম্পন্ন করেছে, যা কৌশল বিকাশকারীদের জন্য একটি বড় আশীর্বাদ। আমরা আমাদের শক্তি এবং সময় কৌশল লজিক ডিজাইন এবং ফাংশন সম্প্রসারণে নিবেদিত করতে পারেন।
এফএমজেড কোয়ান্ট প্ল্যাটফর্মে, বিভিন্ন মূলধারার এক্সচেঞ্জের জন্য ক্যাপসুলযুক্ত ইন্টারফেস রয়েছে। আমাদের যা করতে হবে তা হ'ল এই এপিআই ইন্টারফেসগুলি কল করা। অবশিষ্ট অন্তর্নিহিত বাস্তবায়ন যুক্তিটি একটি পেশাদার দল দ্বারা শেষ হয়েছে।
এই প্রবন্ধে যুক্তি সম্পূর্ণ করতে এবং নীতিটি ব্যাখ্যা করার জন্য, আমরা এই অন্তর্নিহিত যুক্তিগুলি বিস্তারিতভাবে উপস্থাপন করব। তবে, প্রকৃত অপারেশনে, পাঠকরা উপরের চারটি দিক সম্পূর্ণ করতে সরাসরি এফএমজেড কোয়ান্ট এপিআই ইন্টারফেসটি কল করতে পারেন।
আসুন শুরু করা যাক:
১ম ধাপঃ আপনার প্রশ্নটি লিখুন
এখানে, আমরা একটি সংকেত তৈরি করার চেষ্টা করি যা আমাদের বলবে যে অনুপাতটি পরবর্তী মুহুর্তে কিনবে বা বিক্রি করবে, অর্থাৎ আমাদের পূর্বাভাস ভেরিয়েবল Y:
Y = অনুপাত হল কিনুন (1) বা বিক্রি করুন (-1) ।
Y ((t) = Sign ((Ratio ((t+1)
অনুগ্রহ করে মনে রাখবেন যে আমাদের প্রকৃত লেনদেনের লক্ষ্য মূল্য বা এমনকি অনুপাতের প্রকৃত মান (যদিও আমরা করতে পারি) ভবিষ্যদ্বাণী করার প্রয়োজন নেই, তবে পরবর্তী ধাপে শুধুমাত্র অনুপাতের দিকনির্দেশনা।
পদক্ষেপ ২ঃ নির্ভরযোগ্য এবং সঠিক তথ্য সংগ্রহ করুন
FMZ Quant আপনার বন্ধু! আপনি শুধুমাত্র লেনদেনের বস্তু ট্রেড করা হবে এবং ব্যবহার করা তথ্য উৎস নির্দিষ্ট করতে হবে, এবং এটি প্রয়োজনীয় তথ্য আহরণ এবং লভ্যাংশ এবং লেনদেনের বস্তু বিভক্তি জন্য এটি পরিষ্কার করবে। তাই এখানে তথ্য খুব পরিষ্কার।
গত ১০ বছরের ট্রেডিং দিনের (প্রায় ২৫০০ ডেটা পয়েন্ট) উপর আমরা ইয়াহু ফাইন্যান্স ব্যবহার করে নিম্নলিখিত তথ্য পেয়েছিঃ খোলার মূল্য, বন্ধের মূল্য, সর্বোচ্চ মূল্য, সর্বনিম্ন মূল্য এবং ট্রেডিং ভলিউম।
ধাপ ৩ঃ তথ্য বিভক্ত করুন
মডেলের নির্ভুলতা পরীক্ষা করার জন্য এই অত্যন্ত গুরুত্বপূর্ণ ধাপটি ভুলে যাবেন না। আমরা প্রশিক্ষণ/প্রমাণীকরণ/পরীক্ষার জন্য নিম্নলিখিত ডেটা ব্যবহার করছি।
প্রশিক্ষণ ৭ বছর ~ ৭০%
পরীক্ষা ~ ৩ বছর ৩০%
ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]
আদর্শভাবে, আমাদেরও ভ্যালিডেশন সেট তৈরি করা উচিত, কিন্তু আমরা এখনই তা করব না।
ধাপ ৪ঃ ফিচার ইঞ্জিনিয়ারিং
সম্পর্কিত ফাংশনগুলি কী হতে পারে? আমরা অনুপাতের পরিবর্তনের দিকটি পূর্বাভাস দিতে চাই। আমরা দেখেছি যে আমাদের দুটি ট্রেডিং টার্গেটগুলি একীভূত হয়, সুতরাং এই অনুপাতটি পরিবর্তিত হয় এবং গড় মানটিতে ফিরে আসে। দেখে মনে হচ্ছে আমাদের বৈশিষ্ট্যগুলি গড় অনুপাতের কিছু পরিমাপ হওয়া উচিত এবং বর্তমান মান এবং গড় মানের মধ্যে পার্থক্য আমাদের ট্রেডিং সংকেত তৈরি করতে পারে।
আমরা নিম্নলিখিত ফাংশন ব্যবহার করিঃ
৬০ দিনের চলমান গড় অনুপাতঃ চলমান গড়ের পরিমাপ;
৫ দিনের চলমান গড় অনুপাতঃ গড়ের বর্তমান মানের পরিমাপ;
৬০ দিনের স্ট্যান্ডার্ড ডিভিয়েশন;
Z স্কোরঃ (5d MA - 60d MA) / 60d এসডি।
ratios_mavg5 = train.rolling(window=5,
center=False).mean()
ratios_mavg60 = train.rolling(window=60,
center=False).mean()
std_60 = train.rolling(window=60,
center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()
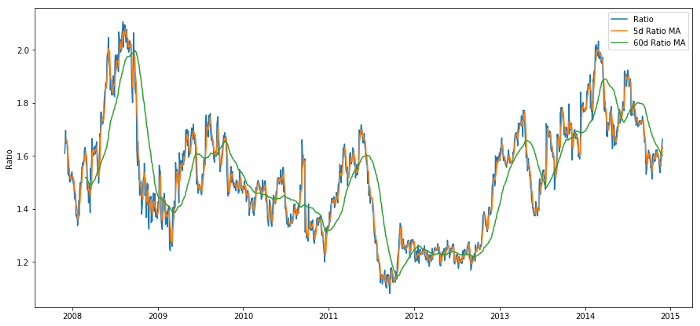
60d এবং 5d MA এর মধ্যে মূল্য অনুপাত
plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()
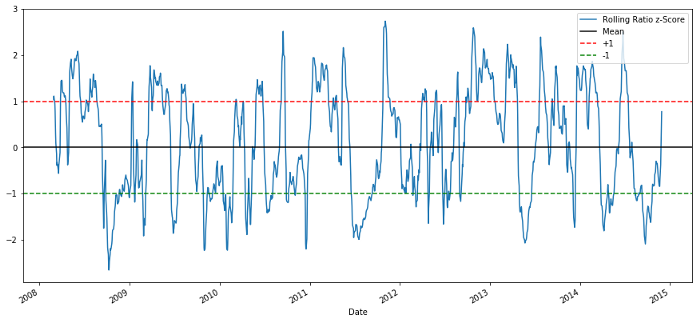
60-5 Z স্কোর মূল্য অনুপাত
চলমান গড় মানের Z স্কোর অনুপাতের গড় মান রিগ্রেশন সম্পত্তি আউট এনেছে!
ধাপ ৫ঃ মডেল নির্বাচন
আসুন একটি খুব সহজ মডেল দিয়ে শুরু করি। z স্কোর চার্টটি দেখে আমরা দেখতে পাচ্ছি যে যদি z স্কোরটি খুব বেশি বা খুব কম হয় তবে এটি ফিরে আসবে। আসুন আমরা খুব বেশি এবং খুব কম সংজ্ঞায়িত করার জন্য আমাদের থ্রেশহোল্ড হিসাবে +1/- 1 ব্যবহার করি এবং তারপরে আমরা নিম্নলিখিত মডেলটি ব্যবহার করতে পারি ট্রেডিং সংকেত উত্পন্ন করতেঃ
যখন z -1.0 এর নিচে থাকে, তখন অনুপাতটি (1) কেনা হয়, কারণ আমরা আশা করি z 0 এ ফিরে আসবে, তাই অনুপাত বৃদ্ধি পায়;
যখন z 1.0 এর উপরে থাকে, তখন অনুপাতটি বিক্রি হয় (- 1), কারণ আমরা আশা করি z 0 এ ফিরে আসবে, তাই অনুপাত হ্রাস পায়।
ধাপ ৬ঃ প্রশিক্ষণ, যাচাইকরণ এবং অপ্টিমাইজেশান
অবশেষে, আসুন আসুন আসল তথ্যের উপর আমাদের মডেলের প্রকৃত প্রভাবটি দেখুন। আসুন আসল অনুপাতের উপর এই সংকেতের পারফরম্যান্সটি দেখুনঃ
# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()
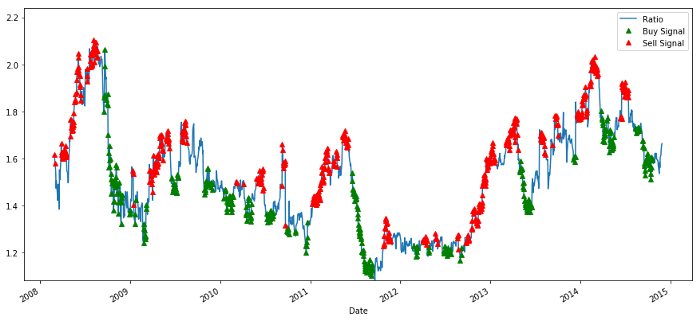
ক্রয় ও বিক্রয় মূল্য অনুপাত সংকেত
সিগন্যালটি যুক্তিসঙ্গত বলে মনে হচ্ছে। আমরা যখন এটি উচ্চ বা বৃদ্ধি পাচ্ছি (লাল বিন্দু) তখন বিক্রি করি এবং যখন এটি কম (সবুজ বিন্দু) এবং হ্রাস পাচ্ছে তখন এটি আবার কিনেছি। আমাদের লেনদেনের প্রকৃত বিষয়বস্তুর জন্য এর অর্থ কী? আসুন দেখুনঃ
# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()
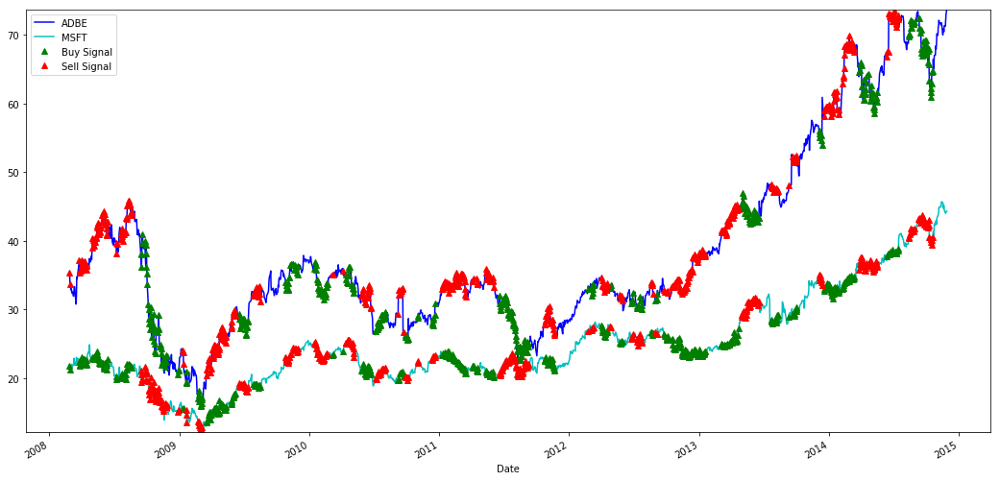
MSFT এবং ADBE শেয়ার কেনার এবং বিক্রি করার সংকেত
অনুগ্রহ করে লক্ষ্য করুন যে আমরা কখনো কখনো
আমরা প্রশিক্ষণ তথ্যের সংকেত দিয়ে সন্তুষ্ট। আসুন দেখি এই সংকেতটি কী ধরনের মুনাফা তৈরি করতে পারে। যখন অনুপাতটি কম হয়, আমরা একটি সহজ ব্যাক টেস্ট করতে পারি, একটি অনুপাত কিনতে পারি (১ টি এডিবিই স্টক কিনুন এবং অনুপাত এক্স এমএসএফটি স্টক বিক্রয় করুন), এবং একটি অনুপাত বিক্রয় করুন (১ টি এডিবিই স্টক বিক্রয় করুন এবং এক্স অনুপাত এমএসএফটি স্টক কিনুন) যখন এটি উচ্চ হয়, এবং এই অনুপাতগুলির পিএনএল লেনদেন গণনা করুন।
# Trade using a simple strategy
def trade(S1, S2, window1, window2):
# If window length is 0, algorithm doesn't make sense, so exit
if (window1 == 0) or (window2 == 0):
return 0
# Compute rolling mean and rolling standard deviation
ratios = S1/S2
ma1 = ratios.rolling(window=window1,
center=False).mean()
ma2 = ratios.rolling(window=window2,
center=False).mean()
std = ratios.rolling(window=window2,
center=False).std()
zscore = (ma1 - ma2)/std
# Simulate trading
# Start with no money and no positions
money = 0
countS1 = 0
countS2 = 0
for i in range(len(ratios)):
# Sell short if the z-score is > 1
if zscore[i] > 1:
money += S1[i] - S2[i] * ratios[i]
countS1 -= 1
countS2 += ratios[i]
print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
# Buy long if the z-score is < 1
elif zscore[i] < -1:
money -= S1[i] - S2[i] * ratios[i]
countS1 += 1
countS2 -= ratios[i]
print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
# Clear positions if the z-score between -.5 and .5
elif abs(zscore[i]) < 0.75:
money += S1[i] * countS1 + S2[i] * countS2
countS1 = 0
countS2 = 0
print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)
ফলাফল হল: ১৭৮৩.৩৭৫
সুতরাং এই কৌশলটি লাভজনক বলে মনে হচ্ছে! এখন, আমরা চলমান গড় সময় উইন্ডো পরিবর্তন করে, ক্রয় / বিক্রয় এবং বন্ধ পজিশনের থ্রেশহোল্ড পরিবর্তন করে, এবং বৈধতা ডেটার কর্মক্ষমতা উন্নতি পরীক্ষা করে আরও অপ্টিমাইজ করতে পারি।
আমরা আরও জটিল মডেল চেষ্টা করতে পারি, যেমন লজিস্টিক রিগ্রেশন এবং এসভিএম, 1/- 1 ভবিষ্যদ্বাণী করতে।
এখন, চলুন এই মডেলকে এগিয়ে নিয়ে যাই, যা আমাদের এনেছে:
ধাপ ৭ঃ পরীক্ষার তথ্য ব্যাক-টেস্ট করুন
এখানেও, এফএমজেড কোয়ান্ট প্ল্যাটফর্মটি ঐতিহাসিক পরিবেশকে সত্যিকার অর্থে পুনরুত্পাদন করতে, সাধারণ পরিমাণগত ব্যাকটেস্টিং ফাঁদগুলি দূর করতে এবং সময়মতো কৌশলগুলির ত্রুটিগুলি আবিষ্কার করতে একটি উচ্চ-কার্যকারিতা QPS / TPS ব্যাকটেস্টিং ইঞ্জিন গ্রহণ করে, যাতে বাস্তব বট বিনিয়োগকে আরও ভালভাবে সহায়তা করতে পারে।
নীতিটি ব্যাখ্যা করার জন্য, এই নিবন্ধটি এখনও অন্তর্নিহিত যুক্তি দেখানোর জন্য বেছে নিয়েছে। ব্যবহারিক প্রয়োগে, আমরা পাঠকদের এফএমজেড কোয়ান্ট প্ল্যাটফর্ম ব্যবহার করার পরামর্শ দিই। সময় সাশ্রয়ের পাশাপাশি, ত্রুটি সহনশীলতার হার উন্নত করা গুরুত্বপূর্ণ।
ব্যাকটেস্টিং সহজ। আমরা উপরের ফাংশনটি ব্যবহার করতে পারি পরীক্ষার ডেটার PnL দেখতে।
trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)
ফলাফলঃ ৫২৬২৮৬৮।
মডেলটি দারুণ কাজ করেছে! এটি আমাদের প্রথম সহজ জোড়া জোড়া ট্রেডিং মডেল হয়ে উঠেছে।
অতিরিক্ত ফিটিং এড়িয়ে চলুন
আলোচনার সমাপ্তির আগে, আমি বিশেষভাবে ওভারফিটিং নিয়ে আলোচনা করতে চাই। ওভারফিটিং হ'ল ট্রেডিং কৌশলগুলির সবচেয়ে বিপজ্জনক ফাঁদ। ওভারফিটিং অ্যালগরিদম ব্যাকটেস্টে খুব ভাল পারফর্ম করতে পারে তবে নতুন অদৃশ্য ডেটাতে ব্যর্থ হতে পারে - যার অর্থ এটি আসলে ডেটাগুলির কোনও প্রবণতা প্রকাশ করে না এবং এর কোনও বাস্তব পূর্বাভাস ক্ষমতা নেই। আসুন একটি সহজ উদাহরণ দেই।
আমাদের মডেলটিতে, আমরা সময় উইন্ডোর দৈর্ঘ্য অনুমান এবং অপ্টিমাইজ করার জন্য রোলিং পরামিতিগুলি ব্যবহার করি। আমরা কেবলমাত্র সমস্ত সম্ভাবনার উপর পুনরাবৃত্তি করার সিদ্ধান্ত নিতে পারি, একটি যুক্তিসঙ্গত সময় উইন্ডোর দৈর্ঘ্য, এবং আমাদের মডেলের সর্বোত্তম পারফরম্যান্স অনুযায়ী সময়ের দৈর্ঘ্য চয়ন করুন। প্রশিক্ষণ ডেটার pnl অনুযায়ী সময় উইন্ডোর দৈর্ঘ্য স্কোর করার জন্য একটি সহজ লুপ লিখুন এবং সেরা লুপটি সন্ধান করুন।
# Find the window length 0-254
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762],
data['MSFT'].iloc[:1762], l, 5)
for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)
('Best window length:', 40)
এখন আমরা পরীক্ষার তথ্যের উপর মডেলের পারফরম্যান্স পরীক্ষা করি, এবং আমরা দেখতে পাই যে এই সময় উইন্ডো দৈর্ঘ্য সর্বোত্তম থেকে অনেক দূরে! কারণ আমাদের মূল পছন্দ স্পষ্টভাবে নমুনা তথ্য overfitted।
# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:],
data['MSFT'].iloc[1762:],l,5)
for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset,
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])
(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)
এটা স্পষ্ট যে আমাদের জন্য উপযুক্ত নমুনা তথ্য সবসময় ভবিষ্যতে ভাল ফলাফল প্রদান করবে না। শুধু পরীক্ষার জন্য, দুটি ডেটা সেট থেকে গণনা দৈর্ঘ্য স্কোর গ্রাফ করা যাকঃ
plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()
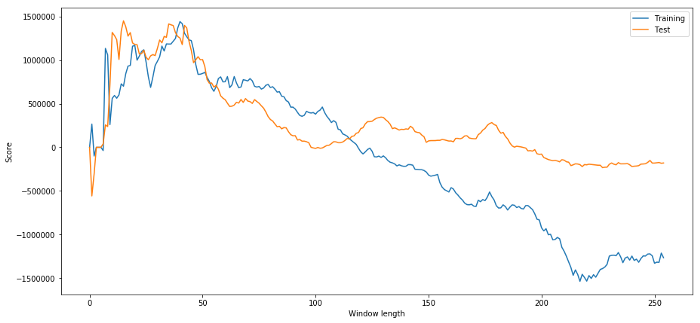
আমরা দেখতে পাচ্ছি যে ২০ থেকে ৫০ এর মধ্যে যেকোনো কিছু সময়ের জন্য একটি ভাল পছন্দ।
ওভারফিট এড়াতে, আমরা সময় উইন্ডোর দৈর্ঘ্য নির্বাচন করতে অর্থনৈতিক যুক্তি বা অ্যালগরিদমের প্রকৃতি ব্যবহার করতে পারি। আমরা কালমান ফিল্টারও ব্যবহার করতে পারি, যা আমাদের দৈর্ঘ্য নির্দিষ্ট করার প্রয়োজন হয় না; এই পদ্ধতিটি পরে অন্য নিবন্ধে বর্ণনা করা হবে।
পরবর্তী ধাপ
এই নিবন্ধে, আমরা ট্রেডিং কৌশল বিকাশের প্রক্রিয়াটি প্রদর্শনের জন্য কিছু সহজ ভূমিকা পদ্ধতি প্রস্তাব করি। অনুশীলনে, আরও জটিল পরিসংখ্যান ব্যবহার করা উচিত। আপনি নিম্নলিখিত বিকল্পগুলি বিবেচনা করতে পারেনঃ
হুরস্ট এক্সপোনেন্ট;
অর্ণস্টাইন-উলেনবেক পদ্ধতি থেকে অনুমান করা গড় রিগ্রেশন অর্ধেক জীবন;
কালমান ফিল্টার।
- ডিইএক্স এক্সচেঞ্জের পরিমাণগত অনুশীলন (2) -- হাইপারলিকুইড ইউজার গাইড
- DEX এক্সচেঞ্জের পরিমাণগত অনুশীলন ((2) -- Hyperliquid ব্যবহারের নির্দেশিকা
- ডিইএক্স এক্সচেঞ্জের পরিমাণগত অনুশীলন (1) -- ডিওয়াইডিএক্স ভি৪ ব্যবহারকারী গাইড
- ক্রিপ্টোকারেন্সিতে লিড-লেগ আর্বিট্রেজের ভূমিকা (3)
- DEX এক্সচেঞ্জের পরিমাণগত অনুশীলন ((1)-- dYdX v4 ব্যবহারের নির্দেশিকা
- ডিজিটাল মুদ্রায় লিড-ল্যাগ স্যুটের ভূমিকা (3)
- ক্রিপ্টোকারেন্সিতে লিড-লেগ আর্বিট্রেজের ভূমিকা (2)
- ডিজিটাল মুদ্রায় লিড-ল্যাগ স্যুটের ভূমিকা (২)
- এফএমজেড প্ল্যাটফর্মের বাহ্যিক সংকেত গ্রহণ নিয়ে আলোচনাঃ কৌশলগতভাবে অন্তর্নির্মিত এইচটিটিপি পরিষেবা সহ সংকেত গ্রহণের জন্য একটি সম্পূর্ণ সমাধান
- এফএমজেড প্ল্যাটফর্মের বহিরাগত সংকেত গ্রহণের অন্বেষণঃ কৌশলগুলি অন্তর্নির্মিত এইচটিটিপি পরিষেবাগুলির সংকেত গ্রহণের সম্পূর্ণ সমাধান
- ক্রিপ্টোকারেন্সিতে লিড-লেগ আর্বিট্রেজের ভূমিকা (1)
- নিউরাল নেটওয়ার্ক এবং ডিজিটাল মুদ্রা পরিমাণগত ট্রেডিং সিরিজ (2) - নিবিড় শিক্ষা এবং প্রশিক্ষণ বিটকয়েন ট্রেডিং কৌশল
- নিউরাল নেটওয়ার্ক এবং ডিজিটাল মুদ্রা পরিমাণগত ট্রেডিং সিরিজ (1) - LSTM বিটকয়েনের মূল্য পূর্বাভাস দেয়
- এসএমএ এবং আরএসআই রিলেটিভ স্ট্রেনথ ইন্ডেক্সের সমন্বিত কৌশল প্রয়োগ
- সিটিএ কৌশল এবং এফএমজেড কোয়ান্ট প্ল্যাটফর্মের স্ট্যান্ডার্ড ক্লাস লাইব্রেরির বিকাশ
- পাইথনে মূল্য গতিবিধি বিশ্লেষণ সহ পরিমাণগত ট্রেডিং কৌশল
- পাইথনে একটি ডুয়াল থ্রাস্ট ডিজিটাল মুদ্রা পরিমাণগত ট্রেডিং কৌশল বাস্তবায়ন করুন
- লিনাক্স ডকারের জন্য ইনস্টল এবং আপগ্রেড করার সর্বোত্তম উপায়
- দীর্ঘ শর্ট পজিশনের সুষম সমন্বয় সহ সুষম মূলধন কৌশল অর্জন
- টাইম সিরিজ ডেটা বিশ্লেষণ এবং টিক ডেটা ব্যাকটেস্টিং
- ডিজিটাল মুদ্রা বাজারের পরিমাণগত বিশ্লেষণ
- ট্রেডিংয়ে মেশিন লার্নিং প্রযুক্তির প্রয়োগ
- ত্রিভুজীয় হেজিংয়ের বিশদ বিশ্লেষণ এবং হেজিংযোগ্য মূল্য পার্থক্যের উপর হ্যান্ডলিং ফিগুলির প্রভাবের জন্য গবেষণা পরিবেশ ব্যবহার করুন
- বিকল্পের পরিমাণগত ব্যবসায়ের সাথে মানিয়ে নিতে ডেরিবিত ফিউচার এপিআই সংস্কার করুন
- ভাল সরঞ্জাম ভাল কাজ করে -- ট্রেডিং নীতি বিশ্লেষণের জন্য গবেষণা পরিবেশ ব্যবহার করতে শিখুন
- ব্লকচেইন সম্পদের পরিমাণগত লেনদেনে ক্রস-ভারেন্সি হেজিং কৌশল
- FMex এর ডিজিটাল মুদ্রা কৌশল গাইড FMZ Quant এ কিনুন
- আপনাকে কৌশল লিখতে শেখাবে -- একটি মাইল্যাঙ্গুয়েজ কৌশল প্রতিস্থাপন (উন্নত)
- আপনাকে কৌশল লিখতে শেখাবে -- মাই ল্যাঙ্গুয়েজের কৌশল প্রতিস্থাপন করবে
- আপনাকে কৌশল মাল্টি চার্ট সমর্থন যোগ করতে শেখান
- পাইথন সংস্করণে একটি কে-লাইন সংশ্লেষণ ফাংশন লিখতে শেখান