Kelly-Formel - ein leistungsstarkes Werkzeug zur Positionskontrolle

Die Wahrscheinlichkeit, dass du gewinnst, ist 60%, die Wahrscheinlichkeit, dass du verlierst, ist 40%. Die Netto-Gewinnrate ist 100%, wenn du gewinnst, und die Verlustrate ist 100%. Das heißt, wenn du gewinnst, kannst du für jeden Dollar 1 Dollar gewinnen, wenn du verlierst, verliert jeder Dollar 1 Dollar.

• 1. Für dieses Staging ist der erwartete Gewinn bei jedem Einsatz 60% des Einsatzbetrags.*1-40%*1 = 20%, erwartete Erträge sind positiv. Das heißt, es ist eine Situation, in der die Hacker überlegen sind und einen sehr großen Vorteil haben.

Wie sollten wir dann wetten?

Wenn wir uns das nicht genau anschauen, dann denken wir uns, dass ich, da ich bei jedem Einsatz einen erwarteten Gewinn von 20 Prozent erwarte, für den langfristigen Gewinn ein größeres Verhältnis des Kapitals in jedem Einsatz einsetzen sollte. Der maximale Wert dieses Verhältnisses ist 100 Prozent.

Aber es ist offensichtlich, dass es nicht vernünftig ist, bei jedem Spiel 100% des Kapitals einzusetzen, denn wenn ein Spieler verliert, verliert er sein gesamtes Kapital und kann nicht mehr an der nächsten Runde teilnehmen, sondern kann einfach aussteigen. Und langfristig gesehen ist es notwendig, dass der Spieler einmal verliert, also muss er langfristig bankrott sein.

Die Schlussfolgerung ist also, dass, solange es eine Chance gibt, dass das gesamte Kapital auf einmal verloren geht, auch wenn diese Möglichkeit sehr gering ist, die Position niemals voll sein kann. Denn auf lange Sicht sind kleine Wahrscheinlichkeitsereignisse zwangsläufig, und in der Realität ist die tatsächliche Wahrscheinlichkeit für ein kleines Wahrscheinlichkeitsereignis viel größer als seine theoretische Wahrscheinlichkeit. Das ist der Saftschwanz-Effekt in der Finanzwissenschaft.

• 2. Zurück zum Stillstand 1. Wenn jeder Einsatz zu 100% unvernünftig ist, wie wäre es dann mit 99%? Wenn man bei jedem Einsatz zu 99% einsetzt, ist es nicht nur garantiert, dass man nie bankrott geht, sondern mit etwas Glück kann man sogar einen großen Gewinn erzielen.

Ist es wirklich so, wie es ist?

Wir analysieren das Problem nicht theoretisch, wir können ein Experiment durchführen. Wir simulieren die Situation und setzen jedes Mal 99 Prozent, um zu sehen, wie es ausgeht.

Die Simulation ist so einfach, dass man sie in Excel durchführen kann.

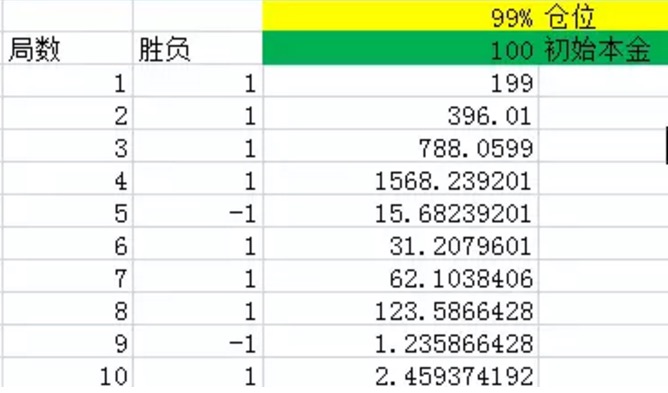Abbildung 1

Die erste Spalte zeigt die Anzahl der Runden. Die zweite Spalte ist der Gewinn, Excel erzeugt 1 mit einer Wahrscheinlichkeit von 60%, d. h. mit einer Wahrscheinlichkeit von 60% wird ein Nettoergebnis von 1,40% erzeugt, d. h. mit einer Wahrscheinlichkeit von 40% wird ein Nettoergebnis von -1 erzeugt. Die dritte Spalte ist der Jackpot mit allen Geldmitteln am Ende jeder Runde.

Wie aus der Grafik zu sehen ist, ist die Wahrscheinlichkeit, dass man nach 10 Runden 8 Runden in 10 Runden gewinnt, größer als 60%, und man verliert nur zweimal. Aber selbst dann bleibt das letzte Geld nur 2,46 Yuan übrig, was im Grunde genommen ein Verlust ist.

Wenn ich die Anzahl der Experimente erhöhe und es zu 1000, 2000 und 3000 … wird es klar, dass das Geld, das wir am Ende haben, sich im Wesentlichen auf 0 bewegt.

Da 99% nicht funktionieren, versuchen wir es mit einigen anderen Proportionen, wie in der folgenden Grafik: Wie man aus der Grafik sehen kann, ist das Ergebnis für die gleichen 10 Runden völlig anders, wenn man die Position allmählich von 99% auf 90%, 80%, 70%, 60% reduziert. Aus der Grafik scheint zu erkennen, dass das Geld nach 10 Runden allmählich größer wird, wenn die Position allmählich kleiner wird.

Wenn man sich das hier anschaut, wird man allmählich erkennen, dass das Problem mit dem Spiel nicht so einfach ist. Selbst wenn es ein Spiel mit so großer Spielmasse ist, in dem die Spieler die Oberhand haben, ist es nicht so einfach, dass jeder Geld gewinnen kann.

Wie kann man also darauf setzen, dass man langfristig die größten Gewinne erzielt?

Ist es so, dass, wie oben gezeigt, je kleiner die Rate, desto besser?

Was ist das optimale Verhältnis?

Das ist das Problem der berühmten Kelly-Formel!

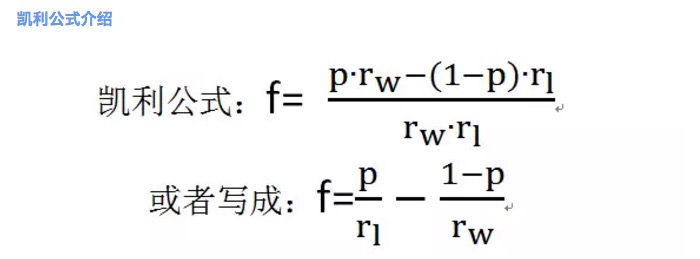Abbildung 2

wobei f das optimale Einsatzverhältnis ist; p die Gewinnwahrscheinlichkeit; rw die Nettoergebnisrate beim Gewinn, z.B. rw = 1 im Spiel 1; rl die Nettoergebnisrate beim Verlieren, z.B. rl = 1 im Spiel 1; beachten Sie, dass rl > 0 ist.

Nach der Kelly-Formel kann man berechnen, dass der höchste Einsatzanteil im Spiel 1 20% beträgt.

Wir können ein Experiment durchführen, um diese Schlussfolgerung zu verstehen.

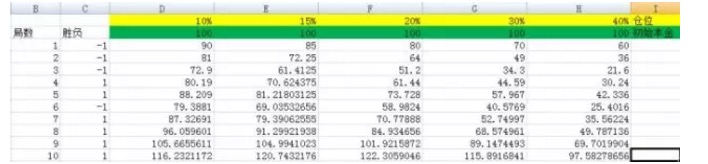Abbildung 3

In der Abbildung haben wir die Positionen auf 10%, 15%, 20%, 30% und 40% festgelegt. Ihre entsprechenden Spalten sind D, E, F, G und H.

Und wenn ich die Anzahl der Experimente auf 3000 erhöhe, Und wenn ich die Anzahl der Experimente auf 5000 erhöhe, Es zeigt sich, dass die F-Reihe das größte Ergebnis hat, und die Druckwurzel im Vergleich zu den anderen Reihen ist keine Größenordnung. Und die Position der F-Reihe entspricht genau 20% .

Sie haben die Kraft der Kelly-Formel gesehen. Wenn Sie in dem Experiment, das oben beschrieben wurde, unglücklich sind, die Rate von 40% zu wählen, also die entsprechende H-Strecke, dann werden Sie nach 5.000 Einsätzen, obwohl Ihr Kapital von 100 auf 22799985.75 ansteigt, einen großen Gewinn erzielen. Aber im Vergleich zu den Ergebnissen mit einer Rate von 20% ist das wirklich das gleiche wie kein Gewinn.

Das ist die Macht des Wissens!

• 3. Die Kelly-Formel verstehen

Die mathematische Schlußfolgerung der Cayley-Formel und ihre Komplexität erfordert sehr hohe und tiefe mathematische Kenntnisse, so dass es hier keinen Sinn macht, darüber zu diskutieren. Hier werde ich durch einige Experimente das subjektive Verständnis der Cayley-Formel vertiefen.

Wenn Sie gewinnen, haben Sie eine Netto-Gewinnrate von 1, also rw = 1, wenn Sie verlieren, haben Sie eine Netto-Verlustrate von 0,5, also rl = 0,5. Das heißt, wenn Sie einen Dollar gewinnen, können Sie einen Dollar gewinnen, wenn Sie gewinnen, und wenn Sie verlieren, müssen Sie nur 5 CZK bezahlen.

Es ist leicht zu erkennen, dass der erwartete Gewinn von Paradox 2 bei 0.25 liegt, ein weiterer Paradox, in dem die Hacker einen enormen Vorteil haben.

Nach der Kelly-Formel erhalten wir die optimalen Wettquoten pro Spiel:

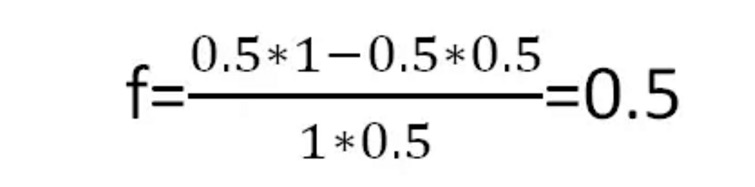Abbildung 4

Das bedeutet, dass jedes Mal, wenn man die Hälfte seines Geldes einsetzt, man langfristig den größten Gewinn erzielt.

Im Folgenden werde ich die Konzeption der durchschnittlichen Wachstumsrate r aus den Experimenten erstellen.

Zuerst betrachten wir Experiment 2.1 mit den folgenden beiden Diagrammen:

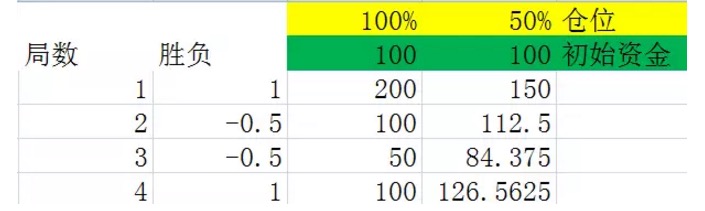Abbildung 5

Diese beiden Diagramme sind Experimente, die mit dem Simulieren von Deadlock 2 durchgeführt wurden. In der zweiten Spalte der Sieg-Strecke gibt es eine 50%ige Wahrscheinlichkeit, dass das Experiment 1 erzeugt, was einen Gewinn von 100% bedeutet. In der zweiten Spalte der 50%igen Wahrscheinlichkeit gibt es -0.5, was einen Verlust von 50% bedeutet. Die dritte und vierte Spalte sind die Positionen von 100% und 50% des Kapitals, das nach jeder Deadlock gehalten wird.

Ein genauer Vergleich der beiden Diagramme zeigt, dass die endgültige Ausgangsergebnisse nur mit der Anzahl der gewonnenen und der Anzahl der verlorenen Runden in diesen Runden zusammenhängen, und nicht mit der Reihenfolge der gewonnenen und der verlorenen Runden in diesen Runden. In den beiden vorherigen Diagrammen wurden beispielsweise 4 Runden durchgeführt, in denen auch zwei Runden in jedem Diagramm gewonnen und verloren wurden, aber die Reihenfolge in der ersten Diagramm war gewinn-verlierer-gewinn, und die Reihenfolge in der zweiten Diagramm war gewinn-verlierer-verlierer.

Natürlich ist diese Schlussfolgerung sehr leicht zu beweisen (die Multiplikations-Austausch-Lehre, das können Kinder lernen), aber das ist kein Beweis, die beiden oben genannten Beispiele reichen aus, um es gut zu verstehen.

Da die endgültige Ausgangsergebnis und die Gewinne und Verluste keine Rolle spielen, gehen wir davon aus, dass die Partie 2 wie in Experiment 2.2 verläuft, wie in der folgenden Abbildung zu sehen ist:

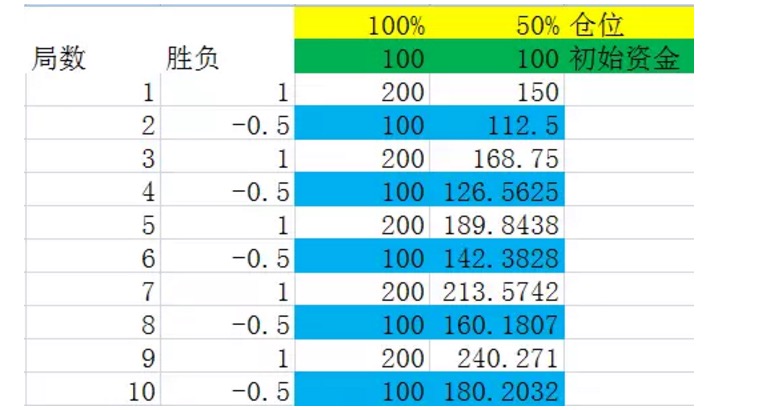Abbildung 6

Wir gehen davon aus, dass der Sieg und die Niederlage im Spiel wechseln, da Schlussfolgerung 1 keinen Einfluss auf das Ergebnis in der langfristigen Sicht hat.

Bevor wir uns das Bild selbst anschauen, definieren wir es. Angenommen, wir betrachten ein paar Ausgangsspiele als ein Ganzes, in dem die Häufigkeit der Ergebnisse genau gleich der Wahrscheinlichkeit ist, und in dem die Anzahl der Ausgangsspiele die kleinste der Mittelzahl aller ausreichenden Ausgangsspiele ist, dann bezeichnen wir dieses Ganze als eine Ausgangsgruppe. Zum Beispiel in den Experimenten in der obigen Abbildung repräsentiert eine Ausgangsgruppe zwei Ausgangsspiele, von denen jeder einmal gewonnen und einmal verloren wird.

Wenn Sie die blau markierten Zahlen in der obigen Grafik genau betrachten, sehen Sie, dass sie am Ende einer Reihe von Stillstands sind. Sie werden feststellen, dass diese Zahlen stetig wachsen. Wenn die Position 100% ist, ist die Wachstumsrate der blau markierten Zahlen 0%, d. h. die Kapitalwachstumsrate nach einer Reihe von Stillstands ist 0%. Dies erklärt auch, dass bei jeder vollen Position kein Gewinn in Spiel 2 in der langfristigen Sicht möglich ist.

Es ist eine allgemeine Regel, dass die Wachstumsrate nach jedem Stillstand mit der Position zusammenhängt. Je höher die Wachstumsrate nach jedem Stillstand ist, desto größer ist der endgültige Gewinn langfristig.

Die durchschnittliche Zuwachsrate für jede Blockade kann anhand der Zuwachsrate für jede Blockade berechnet werden g. In der obigen Abbildung enthält jede Blockade zwei Blockaden, die durchschnittliche Zuwachsrate für jede Blockade

Abbildung 7

In der Praxis ist der optimale Einsatzprozentsatz f durch die Lösung von max (g) möglich.

• 4. Weitere Schlussfolgerungen der Kelly-Formel zum Risiko

Die Legende von Kelly

Die Kelly-Formel wurde ursprünglich für John Larry Kelly, Physiker bei AT&T Bell Laboratories, entwickelt, auf der Grundlage von Forschungen seines Kollegen Claude Elwood Shannon über Langstrecken-Telefonleitungen. Kelly löste die Frage, wie Shannon’s Informationstheorie auf einen Spieler angewendet werden kann, der eine Inline-Nachricht besitzt. Thorpe nutzte seine Arbeitszeit und schrieb eine mathematische Arbeit mit dem Titel “21-Punkte-Spiel-Strategien für die bevorzugte Strategie des Poker”. Er nutzte sein Wissen, um über Nacht alle Casinos in Reno, Nevada zu überfallen und erfolgreich Hunderttausende von Dollar von den 21-Punkte-Spiel-Tischen zu gewinnen. Er war der Urvater des Wall Street Quantitative Trading Hedge Fund in den USA und schuf in den 1970er Jahren den ersten Quantitative Trading Hedge Fund.

Die Nutzung von Perspektive

Wie kann man mit der Kelly-Formel in der Praxis Geld verdienen? Das ist die Idee, eine Schranke zu schaffen, die die Bedingungen der Kelly-Formel erfüllt. Was ist für ein gutes Handelssystem am wichtigsten? Eine positive Erwartungshöhe für die Kauf- und Verkaufsregeln ist 10% der Bedeutung, eine gute Methode zur Kapitalkontrolle ist 40% der Bedeutung, die übrigen 50% sind die psychologischen Kontrollen der Menschen. Die Kelly-Formel hilft mir dabei, meine Kapitalpositionen zu kontrollieren. Ein Beispiel ist ein Aktienhandelssystem, das ich zuvor erforscht habe, das pro Woche einen Handel mit einer Erfolgswahrscheinlichkeit von 0,8 pro Woche durchführt, und die Erfolgswahrscheinlichkeit von 0,2 pro Woche. Wenn es erfolgreich ist, kann ich 3% verdienen (abzüglich der Provisionen und der Stempelsteuer), und bei jedem Misserfolg verliere ich 5%. Bevor ich die Kelly-Formel kannte, war ich blind und handelte mit einer vollen Position und wusste nicht, dass meine Position falsch war. Natürlich kann die Kelly-Formel in der Praxis nicht so einfach sein, und es gibt noch viele Schwierigkeiten, die überwunden werden müssen. Zum Beispiel die Kosten für das Kapital, das eine Leverage-Börse benötigt, zum Beispiel, dass das Geld in der Realität nicht unendlich teilbar ist, zum Beispiel, dass es in den Finanzmärkten nicht so einfach ist wie die einfache Stabilität, die oben erwähnt wurde. Aber die Kelly-Formel zeigt uns den Weg.