Bitcoin-Preisprognose in Echtzeit mithilfe des LSTM-Frameworks

Hinweis: Dieser Fall dient nur der Lern- und Forschungszwecke und stellt keine Investitionsempfehlung dar.

Bitcoin-Preisdaten basieren auf Zeitreihen, daher werden Bitcoin-Preisvorhersagen hauptsächlich mit dem LSTM-Modell durchgeführt.

Die LSM ist ein speziell für Zeitreihen-Daten (oder Daten mit einer Zeit/Raum-/Strukturfolge, wie Filme, Sätze usw.) entwickeltes Deep-Learning-Modell, das als Idealmodell für die Prognose der Kursentwicklung von Kryptowährungen dient.

Der Artikel ist hauptsächlich über die Datenanpassung durch das LSTM geschrieben, um den zukünftigen Preis von Bitcoin vorherzusagen.

Importieren von Bibliotheken

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Datenanalyse

Datenladen

Lesen Sie die täglichen Handelsdaten von BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Die Daten sind in 1380 Datensätzen zu sehen, die aus den folgenden Spalten bestehen: Date, Open, High, Low, Close, Volume (BTC), Volume (Currency) und Weighted Price.

data.info()

Schauen Sie sich die Daten der ersten 10 Zeilen an.

data.head(10)

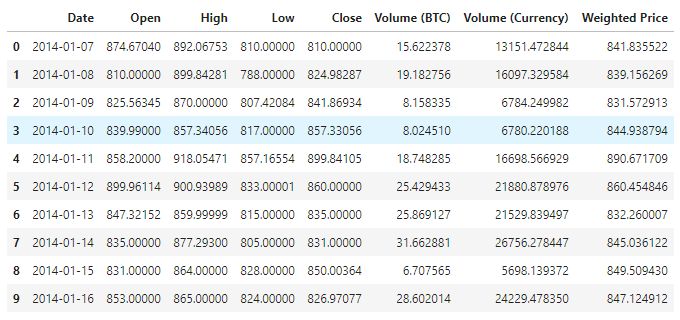
Datenvisualisierung

Matplotlib zeichnet den Gewichteten Preis aus, um die Verteilung und Entwicklung der Daten zu betrachten. In der Abbildung finden wir einen Teil der Daten, der 0 ist, und wir müssen bestätigen, ob die Daten abweichend sind.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

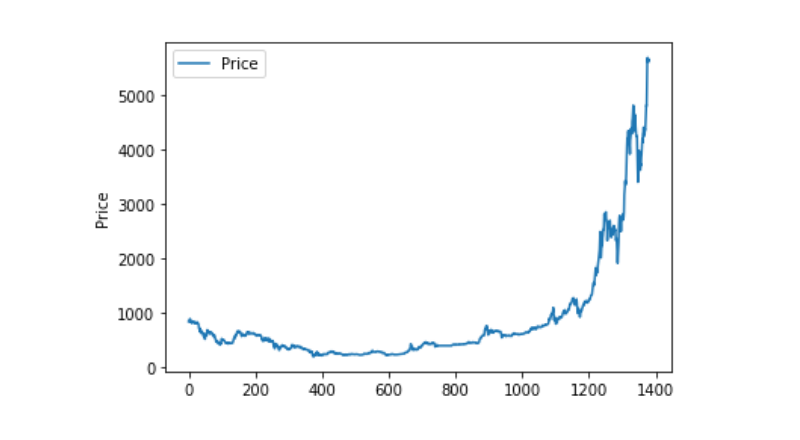
Ausnahmemethoden

Wenn wir also nach unten schauen, ob die Daten Nan enthalten, dann sehen wir, dass es keine Nan-Daten in unseren Daten gibt.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Wenn wir uns die Daten von 0 anschauen, dann sehen wir, dass unsere Daten einen Wert von 0 enthalten, und wir müssen diesen Wert verarbeiten.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Wenn man sich die Verteilung der Daten anschaut, die sich bewegen, dann ist die Kurve sehr kontinuierlich.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Trennungs- und Testdatensätze

Die Daten werden auf 0-1 zusammengefasst.

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Test-Datensätze und Trainings-Datensätze mit 2:8

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Erstellen Sie Training- und Testdatensätze und verwenden Sie einen Tag als Zeitfenster, um unsere Training- und Testdatensätze zu erstellen.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Modelldefinition und Training

Diesmal verwenden wir ein einfaches Modell, dessen Struktur 1. LSTM2. Dense.

Die Input-Dimension der Input-Shape ist batch_size, time steps, features. Die Time-Step-Wert ist der Zeitfensterintervall, in dem die Daten eingegeben werden. Hier verwenden wir 1 Tag als Zeitfenster und unsere Daten sind Tagesdaten, daher sind unsere Zeitschritte hier 1.

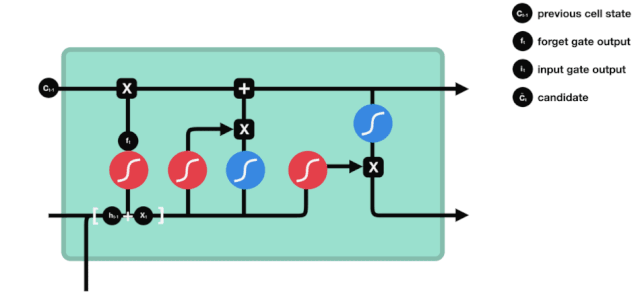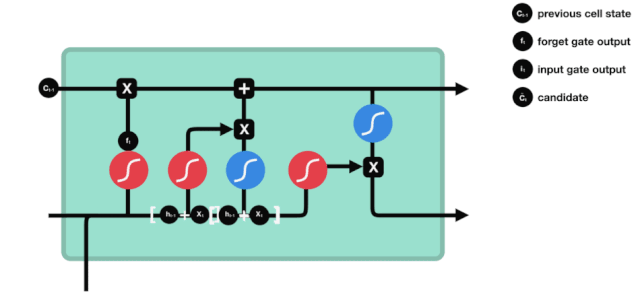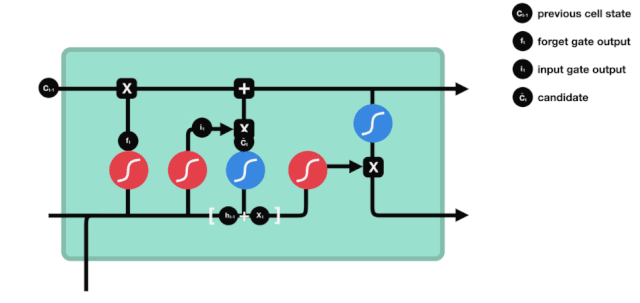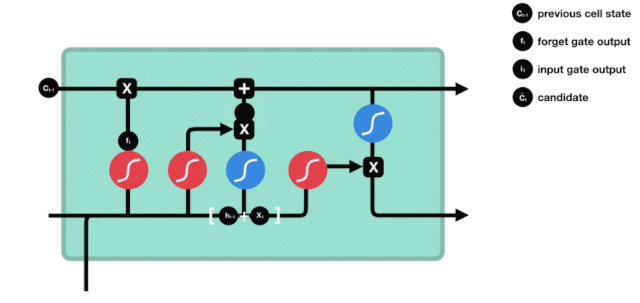
Langes Kurzzeitgedächtnis (LSTM) ist ein spezielles RNN, das hauptsächlich für die Lösung von Verlaufsabbrüchen und Verlaufsausbrüchen während langfristiger Trainingseinheiten verwendet wird.

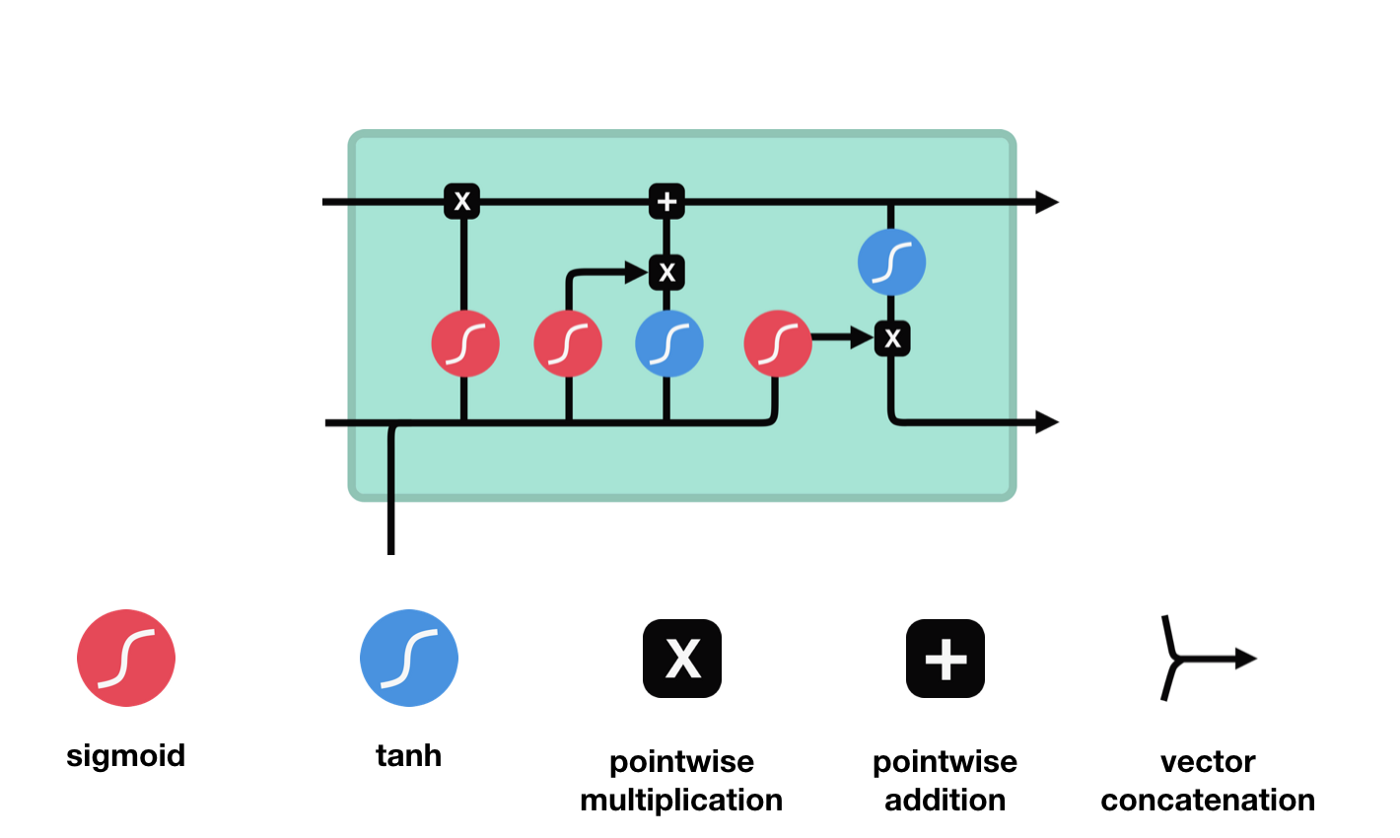
Aus dem Netzwerkstrukturdiagramm von LSTM ist zu sehen, dass LSTM eigentlich ein kleines Modell ist, das 3 Sigmoid-Aktivierungsfunktionen, 2 Tanh-Aktivierungsfunktionen, 3 Multiplikationen und 1 Addition enthält.

Zellzustand

Der Zellzustand ist das Herzstück des LSTM. Er ist die schwarze Linie an der Spitze der Abbildung, und unter dieser schwarzen Linie gibt es ein paar Türen, die wir später beschreiben werden.

Das LSTM-Netzwerk kann Informationen über den Zustand der Zelle über eine Struktur, die als Tor bezeichnet wird, entfernen oder hinzufügen. Das Portal kann selektiv entscheiden, welche Informationen durchlaufen. Das Portal ist eine Kombination aus einer Sigmoid-Schicht und einer Punktmultiplieroperation.

Vergessene Türen

Der erste Schritt des LSTM ist die Entscheidung, welche Informationen der Zellzustand abwerfen soll. Dieser Teil der Operation wird durch eine Sigmoid-Einheit namens Vergessungstor verarbeitet.

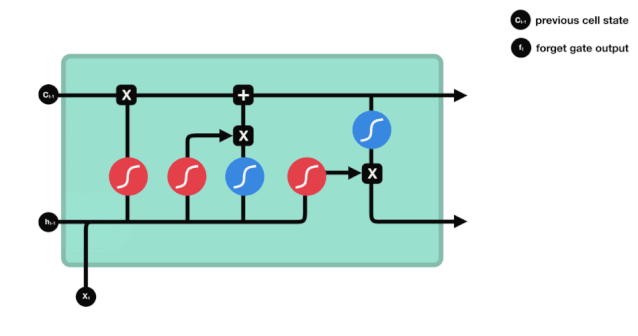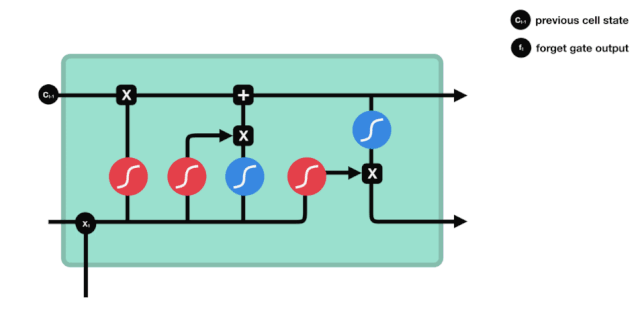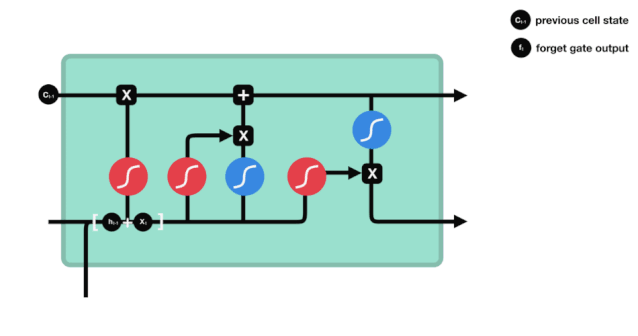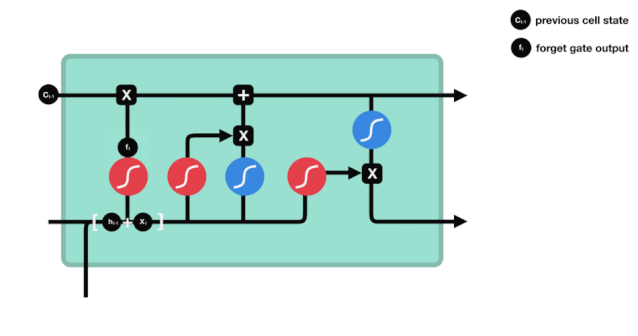
Wir können sehen, dass die Vergesslichkeit ein Vektor zwischen 0 und 1 erzeugt, indem wir die Informationen $h_{l-1}$ und $x_{t}$ betrachten. Der Wert 0 und 1 in diesem Vektor gibt an, wie viel Information im Zellzustand $C_{t-1}$ behalten oder entsorgt wird. 0 bedeutet nicht behalten und 1 bedeutet behalten.

Die mathematische Formel: $f_{t}=\sigma\left ((W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

Einfahrt

Der nächste Schritt ist, zu entscheiden, welche neuen Informationen dem Zellzustand hinzugefügt werden, und dies geschieht durch das Öffnen der Eingabe.

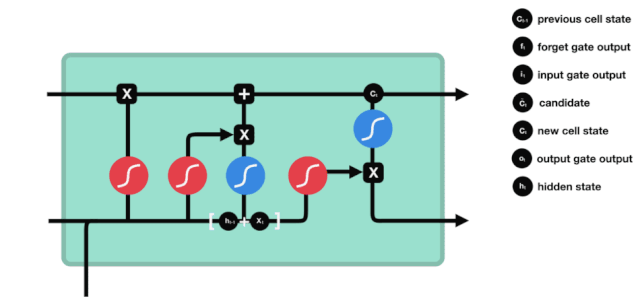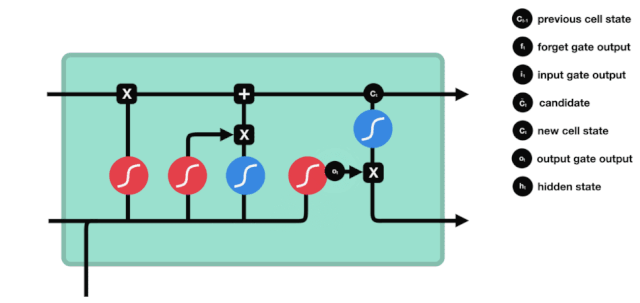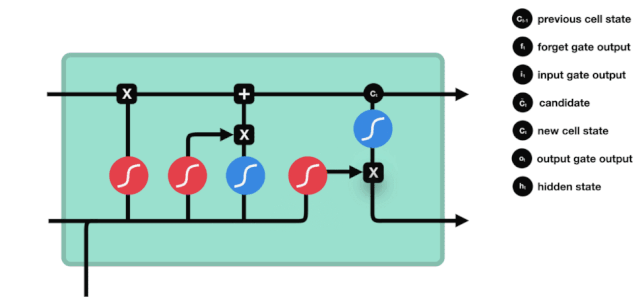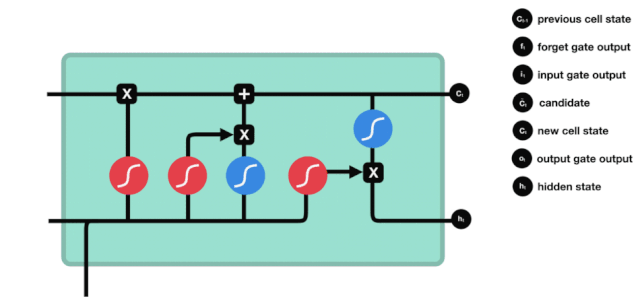
Wir sehen, dass die Informationen von $h_{l-1}$ und $x_{t}$ wieder in ein Vergessungsportal (sigmoid) und in ein Eingangsportal (tanh) eingesetzt werden. Da das Ausgabeergebnis des Vergessungsportals einen Wert von 0 ist, wird das Ergebnis $C_{i}$ nach der Eingabe nicht in den aktuellen Zellzustand hinzugefügt, wenn es 1 ist, wird alles in den Zellzustand hinzugefügt, daher ist die Rolle des Vergessungsportals hier, das Ergebnis des Eingangsortes selektiv in den Zellzustand hinzuzufügen.

Die mathematische Formel lautet: $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t}$

Ausgang

Nach der Aktualisierung des Zellzustands müssen die Zellzustandseigenschaften der Ausgabe anhand der eingegebenen Summen von $h_{l-1}$ und $x_{t}$ beurteilt werden. Hier müssen die Eingabe durch eine Sigmoid-Schicht, die als Ausgangsschlüssel bezeichnet wird, beurteilt werden, und dann der Zellzustand durch die Tanh-Schicht beurteilt wird, um einen Vektor mit einem Wert zwischen -1 und 1 zu erhalten, der mit den Ausgangsschlüssel beurteilten Bedingungen multipliziert wird, um die Ausgabe der endgültigen RNA-Einheit zu erhalten.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

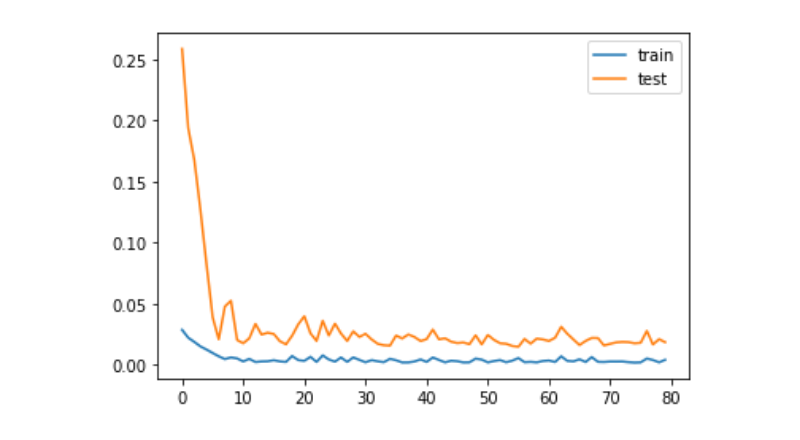
history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Prognose

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

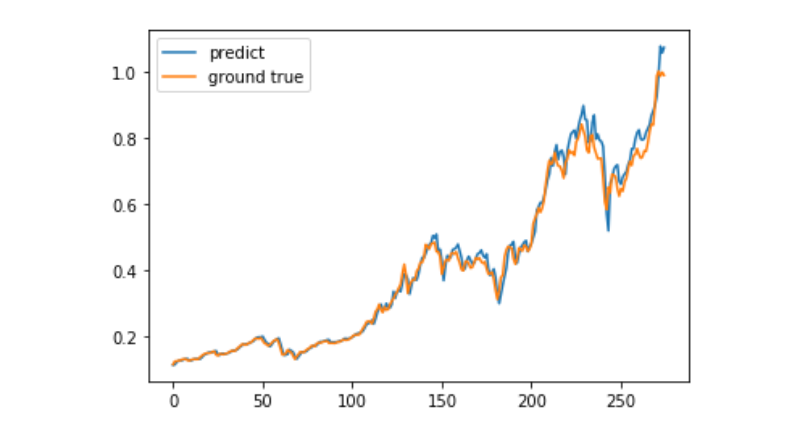
Es ist derzeit sehr schwierig, die langfristige Kursentwicklung von Bitcoin mit Hilfe von maschinellem Lernen vorherzusagen. Dieser Artikel kann nur als Fallstudie verwendet werden. Der Fall wird später in einem Demo-Bild mit der Matrix-Cloud online gestellt, das interessierte Benutzer direkt erleben können.