Urheberrechtserklärung: Bitte geben Sie die Quelle an, wenn Sie den Code des Artikels vervielfältigen möchten. Für kommerzielle Zwecke, schreiben Sie den Artikel bitte per E-Mail oder kontaktieren Sie den Autor auf 940648114@qq.com

1. Einleitung

Die Vorteile von Quantifizierungsgeschäften

Quantitative Handel ist die Subjektivität von Menschen, die durch fortgeschrittene mathematische Modelle ersetzt werden, um Strategien zu entwickeln, die Computertechnologie nutzen, um aus riesigen historischen Daten eine Vielzahl von Ereignissen mit hoher Wahrscheinlichkeit und hoher Wahrscheinlichkeit zu entwickeln, die zu einem übermäßigen Ertrag führen können, um die Auswirkungen von Stimmungsschwankungen der Anleger zu reduzieren und unvernünftige Anlageentscheidungen unter extremen Marktherresien oder -pessimismus zu vermeiden. “Wir haben die Möglichkeit, dass wir uns mit der digitalen Währung auseinandersetzen.*Die kontinuierlichkeit eines 7-Stunden-Unterbrechungs-Trading-Marktes und der Effekt des Quantifizierens von Hochfrequenz-Trading sind offensichtlich ein guter Anfang für die Quantifizierung. Derzeit ist der Markt für digitale Währungen noch unreif.

2. Beschreibung des GQNR-Modells

Das Modell basiert auf dem Garch Modell zur Schwankungsrate-Vorhersage und nutzt eine nichtlineare Regression, z. B. die GA-Kombination zur Vorhersage des oberen VaR und des unteren VaR in der nächsten Zyklus, um die Schwankungsrate durch die VaR-Werte der Spaltungsrückkehr zu prognostizieren. Dieses Modell wird im Folgenden als GQNR bezeichnet.

1. Das Garch-Modul

In diesem Abschnitt werden die Schlussfolgerungen des Kerns der Strategie Garch detailliert beschrieben, die in den Finanzmärkten eine gewisse Allgemeinheit aufweist und in der digitalen Währung eine bestimmte Prognosewirkung erzielt.

1.1 Definition von Garch

Das Wesen des ARCH-Modells besteht darin, dass die q-Ebene der beweglichen Ebene mit einer Quadrature der Restdifferenz den aktuellen Differenzwerten angepasst wird. Da das bewegliche Mittelmodell eine q-Ebene-Schnittstelle der Eigenkorrelationskoeffizienten aufweist, ist das ARCH-Modell eigentlich nur für kurzfristige Eigenkorrelationskoeffizienten der Eigenkorrelationskoeffizienten geeignet. In der Praxis sind jedoch einige Differenzfunktionen für Restsequenzen langfristig eigenständig, was zu einem hohen Moving Average führt, was die Parameterschätzung erschwert und letztendlich die Anpassungsgenauigkeit des ARCH-Modells beeinträchtigt.                                                                                                                                                                    Das GARCH-Modell basiert auf dem ARCH-Modell, welches aus der Eigenregression der p-Klasse der Differenzfunktion hervorgeht, die mit einer Differenzfunktion mit Langzeitgedächtnis effektiv kombiniert werden kann. Das ARCH-Modell ist ein Exemplar des GARCH-Modells, das GARCH-Modell mit p=0 (p,q).

1.2 ARCH-Prozess

Wenn σn die Schwankungen des Vermögenswertes in den n-sten Handelsprozessen und mu die Tagesrendite in den n-ten Handelsprozessen schätzt, kann eine unvoreingenommene Schätzung basierend auf den Renditen der letzten m Handelsprozesse durchgeführt werden: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         Die folgenden Änderungen werden vorgenommen: 1 wird μn-i in die Prozentsatzrendite umgewandelt; 2 wird m-1 in m umgewandelt; 3 wird angenommen, dass μ = 0 ist, und diese Änderungen haben keinen großen Einfluss auf das Ergebnis. \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\( Das heißt, das Quadrat der Schwankungen pro Periode hat das gleiche Gewicht 1/m. Da es sich um Schätzungen der aktuellen Schwankungen handelt, sollten nähere Daten ein höheres Gewicht erhalten. \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$ αi ist der Koeffizient des Quadrats der Rendite für die i-Traditionszyklus, wobei die Summe der Gewichte 1 ist, je kleiner der Wert von i ist. Weiter ausgedehnt, unter der Annahme, dass eine Langzeitdifferenzrate VL vorhanden ist und die entsprechende Gewichtung γ ist, ergibt sich aus der obigen Formel:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

Die Formel 15 kann wie folgt umgeschrieben werden: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( Die übliche ARCH () -Vorgehensweise ergibt sich aus der obigen Formel \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 GARCH-Prozess

Das GARCH (p,q) -Modell ist eine Kombination aus ARCH (p) und EWMA (q), was bedeutet, dass die Schwankungen nicht nur mit den Erträgen der vorherigen P-Phase, sondern auch mit der vorherigen Q-Phase selbst zusammenhängen. $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         Nach der obigen Formel erhalten wir den üblichen GARCH ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 QR-Module

In diesem Abschnitt wird die grundlegende Regression der Dezimalzahlen beschrieben und die strategische Bedeutung der Dezimalzahlen beschrieben.

2.1 QR-Definition

Die Dezimalregration ist eine Methode zur Modellierung der linearen Beziehung zwischen einem Satz von Regressionsvariablen X und den Dezimalen der interpretierten Variablen Y. Die frühere Regressionsmodell ist in der Tat die Erwartung der Bedingungen der zu erklärenden Variablen. Es ist auch die Beziehung zwischen den Mittelwerten der zu erklärenden Variablen und der Verteilung der zu erklärenden Variablen und der Verteilung der Verteilung der Verteilung.

2.2 Von OLS zu QR

Eine allgemeine Regressionsmethode ist die Minimum-Doppel-Multiplikation, d.h. die Summe des Quadrats der Minimierung des Fehlers: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\( Das Ziel der Dezimalzahl ist es, die gewichteten Absolute der Minimierungsfehler auf der Grundlage der obigen Formeln und: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 QR-Visualisierung

Sie können sehen, dass alle Proben durch eine Rücklauflinie in verschiedene Räume aufgeteilt wurden, und diese Rücklauflinie wird zu einer Trennlinie.

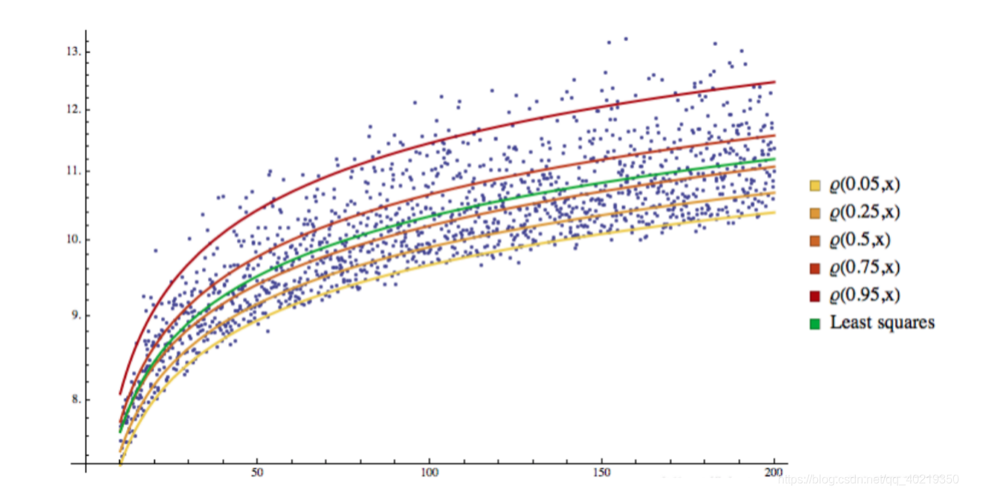
3. GARCH-QR-Rückführung

Es ist natürlich, dass wir uns fragen, ob es möglich ist, mit der unbekannten Marktschwankungsrate Sigma und dem Dezimalwert Q, VaR, eine Regression durchzuführen, um in der Zukunft die Wahrscheinlichkeit zu prognostizieren, dass die Schwankungen in diesem Bereich weitergehen werden.

3.1 Die Wahl der Regressionsform von Volatilität und VaR

Da es sich hier um den Kern der Strategie handelt, werde ich eine Formel vorläufig anführen, um die Idee zu verdeutlichen. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Bestimmung der Zielfunktion

Aufgrund der oben genannten Informationen erhalten wir die endgültig zu optimierende Zielfunktion, die wir durch Kombination erhalten: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Optimierung von Zielfunktionen mit Hilfe von maschinellem Lernen

Der Schritt ist optional, die traditionelle Steigung sinkt, und es gibt auch genetische Algorithmen, mit denen die Leser ihre eigenen Ideen ausprobieren können. Hier wird der optimierte GA-Algorithmus verwendet, der in einem anderen Blog detailliert beschrieben wurde und nicht mehr entwickelt wird.Gibt es eine Adresse für die GA-Algorithmus

3. Wie GQNR in der Quantifizierung eingesetzt wird

1. Die Feststellung der Idee

Der Kern von GQNR liegt in der Volatilität des Marktes, an jedem aktuellen Zeitpunkt kann durch GARCH eine Prognose für die Volatilität der nächsten Periode vorhersagen, auf der anderen Seite kann durch die Dezimalrückkehr der Volatilität der vergangenen Daten eine Volatilitätsniedrigung erzielt werden, die in der höchsten Wahrscheinlichkeit nicht über die Ober- und Untergrenze hinausgeht. Diese beiden Grenzen sind der Kern der Gesamtheit.

2. Schwierigkeiten bei der Anwendung

• Die Form der Rückkehr
• Die Wahl eines Adaptive-Algorithmus
• Die richtigen Parameter für Machine Learning
• Unsicherheit und Zufälligkeit

3. Die Lösung

• Verkürzung der Zeitspanne, in der Strategien erlernt werden
• Verringerung der langfristigen Risiken durch die Einmalbürgschaft
• Erhöhung der Co-Verifizierung von Doppel-Gleichgewichtstrends und der Bestätigung von Zweitverlusten