Lauch und die Geld-Brief-Spanne: Eine vorläufige Studie zum EKOP-Modell

• #### 1. Vorwort

Die letzten Tage waren außergewöhnlich geschäftig, und seit dem letzten Mal, als ich einen Artikel geschrieben habe, sind schon einige Monate vergangen. In diesen Monaten sind viele Dinge passiert, von denen einige für mein eigenes Leben unabdingbare schwarze Schwämmen waren. Aber diese Erfahrungen haben mir gezeigt, dass das Leben, wie der Handel, mit Höhen und Tiefen und voller Unbekannter ist.

Wir alle wissen, dass eine Aktie, die aktiv gehandelt wird, in der Regel einen geringeren Kauf- und Verkaufspreis hat, während eine Aktie, die nicht aktiv gehandelt wird, den Gegenteil hat. Warum kommt das vor? Kann man die Preisunterschiede mit einem einfachen, schönen mathematischen Modell erklären?[Die Anwendung des Modells wird in einem späteren Artikel (wenn ich Zeit habe) weiter analysiert. Die Schönheit der mathematischen Modelle ist, dass die Lässigkeit des Artikels genügend ist, und das Lesen des Artikels ist eine Freude.

• #### 2. Die Annahme des Transaktionsprozesses

Wenn wir über ein Finanzmodell sprechen, ist es am wichtigsten, sich mit den Annahmen zu befassen. Gute Finanzmodelle haben ihre eigenen Annahmen: Sie sind nicht zu stark, um nicht allgemeingültig zu sein, und sie sind nicht zu schwach, um nicht schöne und prägnante Ergebnisse abzuleiten. Die Grundannahmen des EKOP-Modells sind:

Hypothese 1: Wir sprechen über den Handel mit Aktien, der sich auf getrennte Tage und kontinuierliche Tagesgeschäfte beschränkt. Das heißt, die Geschäfte der Händler finden an 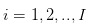an diesen getrennten Geschäftstagen statt. Während die Geschäfte an 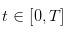an diesen Tagen stattfinden.

• Schlechte Nachrichten, wir notieren den Wert der Aktie als
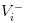
• Gute Nachrichten: Wir notieren den Wert der Aktie als
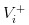
• Es gibt keine Nachrichten, wir notieren den Wert der Aktie als

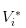
Es ist klar, dass wir 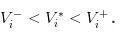haben

Hypothese 2: An einem bestimmten Tag gibt es α

Die Wahrscheinlichkeit, dass ein Ereignis eintritt, das den Aktienpreis beeinflusst, ist 1-α für ein Ereignis, das den Aktienpreis nicht beeinflusst. An den Tagen, an denen ein Ereignis eintritt, gibt es eineδ Wahrscheinlichkeit für ein schlechtes Ereignis, das den Aktienpreis senkt, und eineδ Wahrscheinlichkeit für ein gutes Ereignis, das den Aktienpreis erhöht.

Hypothese 3: Die Teilnehmer am Börsengeschäft sind Market Maker, Informed Trader und Uninformierte Trader. Sie verhalten sich wie folgt:

MM ist immer bereit, eine Einheit zu kaufen oder zu verkaufen, um seine Pflicht als Market Maker zu erfüllen. MM ist risikoneutral, daher ist der Preis, den er anbietet, der Preis, den er für gerecht hält.

IT handelt nur an den Tagen, an denen Nachrichten kommen, und ihr Handel ist ein entspannter Prozess. An einem bestimmten Tag, wenn schlechte Nachrichten kommen, wird er mit einer Ankunftsrate von μ ein Kaufschein aufhängen; an den Tagen, an denen gute Nachrichten kommen, wird er mit einer Ankunftsrate von μ ein Kaufschein aufhängen.

UT, also unsere armen Zitrusfrüchte, sind aufgrund der Vorteile der Nachrichtlosigkeit auch ein lockerer Handelsprozess, der jeden Tag mit einer Ankunftsrate aufgehängt wird. Beachten Sie, dass alle Poson-Prozesse hier unabhängig voneinander sind. Wir können Hypothese 3 mit einer Abbildung darstellen, wie folgt:

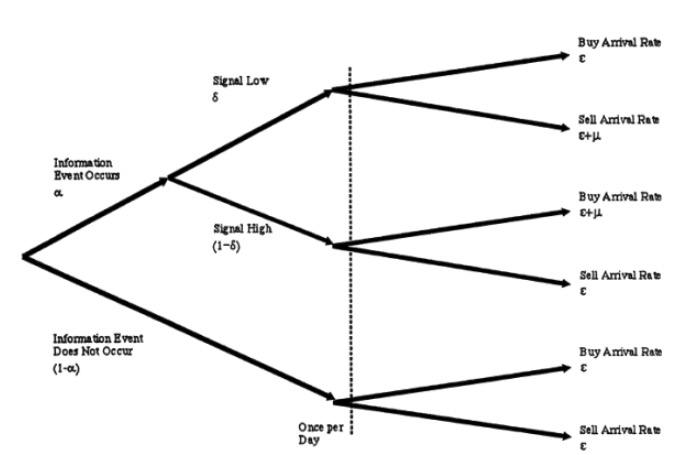
• #### 3 Aktualisierungen von Transaktionen und Preisen

Wir wissen, dass es sich bei einem Marktvertreter meist um ein großes Unternehmen handelt, das sich mit IT und IT auseinandersetzt. Sie sind klug und haben alle Modellparameter in der obigen Baumkarte durch eine große Menge an historischen Datenanalysen zusammengefasst. Glücklicherweise sind sie nicht so gut wie die informierten Händler, die nicht wissen, ob etwas Wichtiges am heutigen Tag passiert ist, wenn ein Handelstag gerade beginnt.

Nun, lassen Sie uns gemeinsam die Rolle eines MM erleben, der mit den IT und den UT kämpft. In einer Zeit von t haben wir uns selbst als einen Vektor für die Wahrscheinlichkeit von Nichts, Gutes und Schlechtes eingetragen.

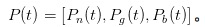。 Es ist offensichtlich, dass ich zu Beginn des Tages, also zu der Zeit, als 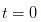erschien, keine Einladung gesehen habe, also kann ich nur annehmen, dass die Wahrscheinlichkeit, dass nichts passiert, α ist, die Wahrscheinlichkeit, dass etwas Gutes passiert, /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, und die Wahrscheinlichkeit, dass etwas Schlechtes passiert, /upload/asset/87418f07b12fce65f4c3f70b024e94d2e19f769a.png.

Wie sollte man diese Wahrscheinlichkeit aktualisieren? Gut, wir, die wir die Wahrscheinlichkeiten der Börsen wählen, kennen die Bayes-Formel. Wenn wir beobachten, dass ein Verkauf kommt, dann benutzen wir das Bayes-Gesetz, um unsere eigenen Wahrscheinlichkeitsschätzungen zu aktualisieren.

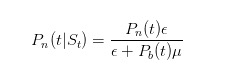
Die Formel besagt, dass nur uninformierte Händler bei fehlender Nachricht ein Ticket unter ε verkaufen, während die Division besagt, dass uninformierte Händler zu jeder Zeit ein Ticket unter ε verkaufen und informierte Händler nur bei schlechten Ereignissen ein Ticket unter μ verkaufen.

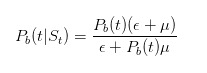
und

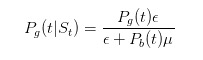
Bevor wir weitermachen, lassen Sie uns ein paar einfache Tests durchführen. Wir haben gesagt, wenn wir eine Verkaufslizenz sehen, sollten wir die Wahrscheinlichkeit für ein schlechtes Ereignis erhöhen.

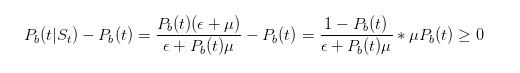
Es ist offensichtlich, dass unsere Schlussfolgerungen unsere Intuition bestätigen.

Mit der aktualisierten Wahrscheinlichkeit können wir den fairen Preis berechnen, der als unser Kaufpreis auf dem Markt gilt, der in der Formel

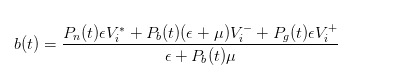
Durch eine ähnliche Schlussfolgerung können wir feststellen, dass der Verkaufspreis, den wir als Makler angeben, wenn ein Kaufbefehl eingeht,

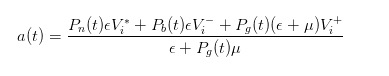
• #### 4 Preisdifferenz-Ausdruck nach Preisanpassung

Die obige Formulierung von Kauf- und Verkaufspreis ist nicht intuitiv genug, wir können den Erwartungswert der Aktie zum Zeitpunkt t einfügen, um die Formulierung zu vereinfachen.

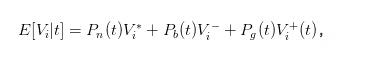
So können wir die Ausdrücke von Bid und Ask in

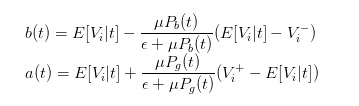
Wir können also die Preisunterschiede klar als

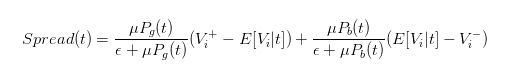
• #### 5 Einfluss des Handelns auf die Preisunterschiede

Wenn wir die Unterschiede in den Preisen kennen, können wir die Auswirkungen der verschiedenen Händler auf die Unterschiede analysieren.

Je mehr Spinach, desto geringer ist die Differenz. Beachten Sie, dass ε die Erreichbarkeit von unwissenden Händlern ist (wir nennen sie Spinach-Pinaches), und wenn es ε >> μ gibt, können wir feststellen, dass / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png Beide Punkte auf 0 gehen, was bedeutet, dass der Spread auch auf 0 geht. 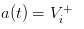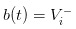Wenn wir noch weiter gehen und davon ausgehen, dass es keine Spinach mehr auf dem Markt gibt, sondern nur eine Gruppe von sachkundigen Händlern, die noch besser sind als Sie, dann werden wir traurig feststellen, dass der Preis, den wir anzeigen, und ist.

Sie sehen, dass wir aufgrund einiger Annahmen, mit Hilfe sehr einfacher mathematischer Schlüsse, zu so interessanten und tiefgründigen Schlussfolgerungen kommen können, und das ist wahrscheinlich der große Reiz der mathematischen Modelle.

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.