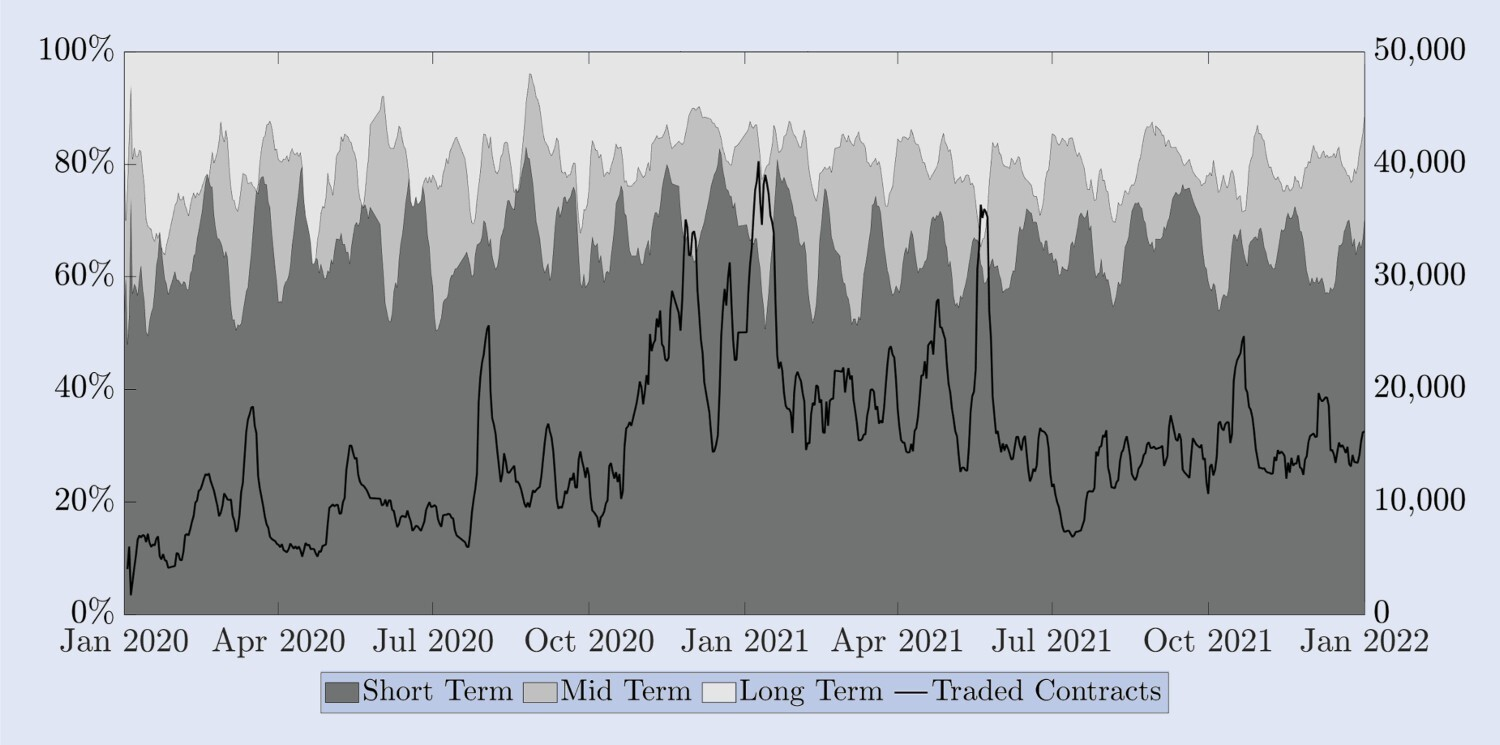
rakte mit Verfallsdaten von mehr als einem Monat relativ stabil geblieben. Dies gilt auch für den Anteil kurzfristiger Optionen mit einem Verfallsdatum innerhalb von zwei Wochen. Tatsächlich liegen etwa 60 % aller gehandelten Kontrakte in diesen sehr kurzfristigen Verfallszeiträumen. Weitere 20 bis 25 Prozent der gehandelten Kontrakte entsprechen „mittelfristigen“ Optionen mit Laufzeiten zwischen zwei Wochen und einem Monat. Da Optionen mit einer Laufzeit von einem Monat 80–85 % des gesamten Handelsvolumens auf Deribit ausmachen, haben wir beschlossen, unsere Absicherungsforschung auf diese Optionen zu konzentrieren. Optionen mit Laufzeiten von mehr als einem Monat weisen selbst bei stündlichen Frequenzen zu viele veraltete Preise auf, um für unsere empirische Analyse nützlich zu sein. Dies veranlasst uns, in jeder der oben dokumentierten Ablaufkategorien eine Option in Betracht zu ziehen. Um den Vergleich zu erleichtern, haben wir als Untersuchungsobjekte Optionen mit konstanter Verfallszeit von 10, 20 und 30 Tagen ausgewählt, die jeweils einen Proxy für die drei wichtigsten Verfallskategorien darstellen.

Abb. 6. Verfallsdatum der gehandelten Optionen.

Die Skala links zeigt den Anteil kurzfristiger Optionen (bis zu zwei Wochen, dunkelgrau), mittelfristiger Optionen (zwischen zwei Wochen und einem Monat, mittelgrau) und langfristiger Optionen (mehr als ein Monat, hellgrau) am gesamten Handelsvolumen. Die schwarze Linie (rechte Skala) stellt die Gesamtzahl der gehandelten Optionskontrakte dar. Bei allen Reihen handelt es sich um gleitende Wochendurchschnitte der Tagesdaten.

Als nächstes besprechen wir die Datenfilterung. Selbst wenn wir uns nur auf Optionen mit einem Verfallsdatum von einem Monat konzentrieren, müssen wir dennoch einige veraltete Preise herausfiltern, d. h. Optionspreise, bei denen in den letzten 24 Stunden kein Handelsvolumen festgestellt wurde. Auch bei Daten zu Futures-Kontrakten mit begrenzter Laufzeit ist die Liquidität ein zentrales Thema, da veraltete Futures-Preise zu Fehlern bei der Delta-Berechnung von Optionen führen können. Aus diesem Grund ziehen wir es vor, zur Ermittlung des korrekten Futures-Preises die Call-Put-Paritätsbeziehung (PCP) zu verwenden, statt den Marktpreis heranzuziehen, wie wir es bei sehr liquiden unbefristeten Kontrakten tun. Bei Bedarf filtern wir Optionsmittelpreise heraus, die die von Fengler (2009) vorgeschlagene Arbitragefreiheitsbedingung verletzen, und leiten die implizite Volatilität aus den verbleibenden Preisen zurück. Es ist zu beachten, dass die Liquidität und Handelsaktivität von OTM-Optionen viel höher sind als die von ITM-Optionen mit demselben Ausübungspreis. Daher verwenden wir die implizite Volatilität von Put-Optionen, um den Fall von m < 1 zu berechnen, und verwenden die implizite Volatilität von Call-Optionen. Die Volatilität wird zur Berechnung des Falls m ≥ 1 verwendet. Es ist wichtig zu beachten, dass der Unterschied zwischen der impliziten Volatilität der ATM-Call- und Put-Optionen nahezu vernachlässigbar ist. Dadurch können wir aus der impliziten Volatilitätsoberfläche des Marktes ein Rohraster erstellen und dann interpolieren, um gefilterte Preise zu erhalten, wie unten beschrieben.

Um eine kontinuierliche historische Reihe jedes Optionspreises zu erhalten, konstruieren wir die Preise synthetischer Kontrakte mit konstantem Verfallsdatum und vorgegebenen Geldeigenschaften. Die kurzfristigen Optionen werden durch ein festes Verfallsdatum von 10 Tagen dargestellt, die mittelfristigen Optionen liegen bei 20 Tagen und für die langfristigen Optionen ziehen wir ein Verfallsdatum von 30 Tagen in Betracht. Da der Bitcoin-Preis häufig Trendänderungen unterliegt, ist es unmöglich, denselben Ausübungspreis über einen langen Zeitraum hinweg zu vergleichen. Daher haben wir auch einen geeigneten Bereich monetärer Eigenschaften für die Interpolation ausgewählt. Wir finden ausreichend Volumen innerhalb einer Ausübungspreisspanne von etwa 30 % über und unter dem Bitcoin-Niveau. Daher interpolieren wir die synthetischen Optionspreise für jede konstante Laufzeit und Geldeigenschaft m∈{0,7,0,8,0,9,1,1,1,1,2,1,3} Anmerkung 15. Tatsächlich verwenden wir die von Fengler (2009) vorgeschlagene Interpolationsmethode auf der impliziten Volatilitätsoberfläche unter der Arbitragefreiheitsgrenze. Fengler schlägt außerdem eine natürliche kubische Spline-Interpolationsmethode vor, um die implizite Volatilitätsoberfläche zu glätten. Allerdings variiert die Form der impliziten Volatilitätskurve für Bitcoin viel stärker als für andere Optionstypen und wir stellen fest, dass die kubische Spline-Interpolation zu flexibel und empfindlich auf große Intervalle zwischen bestimmten Ausübungspreisen reagiert. Daher verwenden wir formerhaltende stückweise kubische Hermite-Polynome, um die implizite Volatilitätsoberfläche zu interpolieren und überprüfen anschließend den Preis, um sicherzustellen, dass die Arbitragefreiheitsbeschränkung der Konvexität in Bezug auf den Ausübungspreis nicht verletzt wird. Diese Technik wurde in vielen anderen akademischen Studien angewendet, beispielsweise von Malz (1997) und Bliss und Panigirtzoglou (2002).

Zunächst interpolieren wir die Smiley-Kurve der impliziten Volatilität, um unter Verwendung formerhaltender stückweise kubischer Hermite-Polynome eine implizite Volatilität mit konstanter Geldmäßigkeit unter der von Fengler (2009) vorgeschlagenen Arbitragefreiheitsbeschränkung zu erhalten. Als nächstes ermitteln wir die implizite Volatilität von Optionen mit konstanter Laufzeit und konstanter Geldmenge durch Interpolation der Volatilitäts-Termstruktur und verwenden diese implizite Volatilität zur Erstellung synthetischer Optionspreise (Anmerkung 16). Um jegliche Kalenderarbitragemöglichkeiten zu vermeiden, stellen wir sicher, dass die gesamte implizite Varianz mit dem Ablaufdatum zunimmt. Um die Absicherungsleistung zu bewerten, müssen wir außerdem den Preis jeder synthetischen Option innerhalb eines Zeitinkrements aufzeichnen, ohne den Straddle zu ändern, der zur Konstruktion der entsprechenden Option verwendet wurde. Nur dieser Rahmen ermöglicht es uns, die Gewinne und Verluste eines dynamischen Absicherungsportfolios zu erfassen. Daher haben wir mit den soeben beschriebenen Methoden synthetische Futures und Optionen erstellt, um aktualisierte Geldwerte und Optionspreise mit Verfallsdaten von 9, 19 und 29 Tagen für den täglichen Datensatz zu erhalten. In ähnlicher Weise konstruieren wir im 8-Stunden-Datensatz Futures und Optionen mit Verfallsdaten, die 8 Stunden, weniger als 10, 20 und 30 Tage entfernt sind. Insgesamt haben wir ungefähr 175.000 synthetische Optionspreise mit Tagesfrequenz und 88.000 Hedge-Verhältnisse sowie über 525.000 synthetische Optionspreise mit 8-Stunden-Frequenz und über 263.000 Hedge-Verhältnisse generiert.

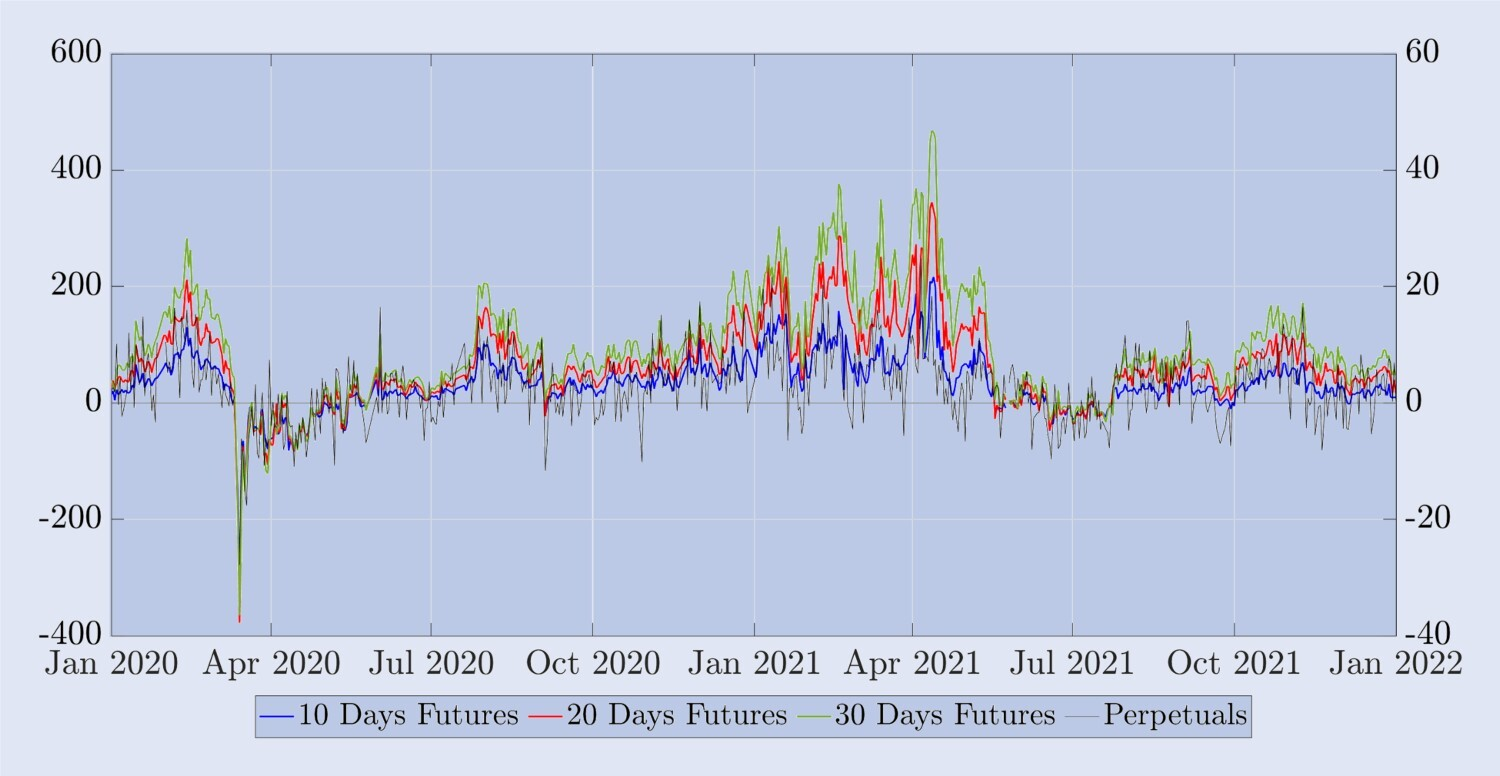
Als Nächstes werden wir einige empirische Merkmale unbefristeter Bitcoin-Verträge untersuchen und sie mit Futures mit fester Laufzeit vergleichen, bevor wir mit unserer Absicherungsstudie fortfahren. Der Abrechnungspreis von Bitcoin-Optionen ist kein handelbarer Kontrakt, daher müssen wir Futures oder unbefristete Kontrakte als Absicherungsinstrumente nutzen. Dabei hängt die Effektivität der Nutzung von Futures-Kontrakten zur Absicherung von Optionen unter anderem von der Variabilität der Basis ab. Um diese Variabilität zu veranschaulichen, zeigt Abbildung 7 die Differenz zwischen dem Terminmarktpreis (oder unbefristeten Kontrakt) und dem BTC-Index, geteilt durch den BTC-Index. Diese prozentuale Basis wird in Basispunkten (Bp) ausgedrückt, wobei die linke Skala für die drei synthetischen Futures mit fester Laufzeit und die rechte Skala die Basis im Verhältnis zum unbefristeten Kontrakt darstellt. Aufgrund des Finanzierungssatzmechanismus ist das Basisrisiko unbefristeter Futures sehr gering – meistens weniger als ±10 Basispunkte. Allerdings ist er auch sehr volatil. Während des COVID-Crashs im März 2020 beispielsweise erreichte die unbefristete Basis fast -150 Basispunkte. Unbefristete Kontrakte weisen ein sehr geringes Basisrisiko auf, was darauf schließen lässt, dass sie ein besseres Absicherungsinstrument darstellen könnten als Kalender-Futures mit demselben Optionsverfallsdatum. Im Gegensatz zur unbefristeten Basis ist die Basis für Futures mit fester Verfallszeit fast immer positiv. Bei 10-Tages-Futures kann die Basis bis zu 100 Basispunkte betragen, während sie bei längerfristigen Futures sogar 450 Basispunkte erreichen kann. Wie aus diesem Diagramm ersichtlich ist, weisen die 10-, 20- und 30-Tage-Futures-Kurven im Allgemeinen eine positive Prämie auf - tatsächlich lautet die Reihenfolge an 620 der 730 untersuchten Tage F30>F20>F10 und nur im März 2020 ändert sich die Reihenfolge. Die gegenteilige Entwicklung ereignete sich im Juni/April (der COVID-Absturz und seine Folgen) und Juni/Juli 2021 (das Ende des langen Bullenlaufs von Bitcoin).

Abbildung 7. Unterschiede zwischen Spot- und unbefristeten Kontrakten sowie Futures.

Der Futures-Preis abzüglich des BTC-Index, geteilt durch den BTC-Index, ausgedrückt in Basispunkten. Die rechte Skala misst den Basisprozentsatz für unbefristete Futures (schwarz) und die linke Skala misst den Basisprozentsatz für Futures mit festen Verfallsdaten von 10, 20 und 30 Tagen (blau, rot bzw. grün). Die Stichprobe umfasst einen Zeitraum von zwei Jahren ab Januar 2020, wobei täglich um Mitternacht UTC Schnappschüsse gemacht werden.

Ein weiterer Faktor, der den Erfolg einer dynamischen Delta-Arbitrage-Strategie beeinflusst, sind die Transaktionskosten. Wenn die Geld-Brief-Spanne des abgesicherten Instruments groß ist, kann eine häufige Neugewichtung der Delta-Arbitrage (in unserem Fall nicht nur täglich, sondern alle 8 Stunden) die Performance der Absicherung beeinträchtigen. Für jede Option kann das Delta jedoch nicht zwischen extrem unterschiedlichen Werten schwanken. So wird beispielsweise eine Call-Option nahe am Geld immer ein Delta nahe 0,5 haben, unabhängig vom verwendeten Modell - siehe Vähämaa (2004) für eine Beispiel. Daher können unterschiedliche Delta-Werte nur dann einen signifikanten Einfluss auf die Absicherungsleistung haben, wenn die Geld-Brief-Spanne groß ist. Allerdings sind die Geld-Brief-Spannen bei unbefristeten Futures gering, und sogar die Geld-Brief-Spannen bei Kalender-Futures sind gering. Bei unbefristeten Futures übersteigt die Geld-Brief-Spanne selten einen Mindestwert von 0,50 USD, was je nach Preisniveau 0,1 bis 0,25 Basispunkten entspricht. Kalender-Futures weisen etwas größere Geld-Brief-Spannen auf und steigen mit zunehmendem Verfallsdatum an, aber auch diese Spannen sind in unserer Stichprobe sehr klein. Selbst bei Futures-Kontrakten mit der längsten Laufzeit übersteigen die Spreads selten 5 Basispunkte und liegen meist bei etwa 1 Basispunkt. Eine so geringe Spanne hat kaum Einfluss auf unsere Vergleiche zwischen verschiedenen Delta-Werten, daher werden wir sie in der folgenden empirischen Untersuchung ignorieren.

6. Empirische Hedgingforschung

Inspiriert von unserer Diskussion in den Abschnitten 2, 3 und 5 behandeln wir inverse Optionen wie normale Devisenoptionen, d. h. wir verwenden den aktuellen Wert der zugrunde liegenden Option, um ihren Bitcoin-Preis in den entsprechenden USD-Wert umzurechnen. Wir wählen feste Verfallsdaten von 10, 20 und 30 Tagen für synthetische kontinuierliche Futures- und Optionspreise und die Geldmäßigkeit der Optionen wird zwischen 0,7 und 1,3 gewählt. Unsere Daten basieren auf Hedges, die alle 8 Stunden oder täglich neu gewichtet werden. Die Stichprobe umfasst einen Zweijahreszeitraum vom 1. Januar 2020 bis zum 1. Januar 2022, aufgeteilt in zwei Einjahreszeiträume. Beispiele zur Darstellung der Ergebnisse. Zu jedem Zeitpunkt t verkaufen wir eine europäische Option mit der Währung m und dem Verfallsdatum T und sichern sie mit einem unbefristeten Kontrakt oder einem Futures-Kontrakt mit demselben Verfallsdatum wie die Option ab. Gewinne und Verluste werden als Absicherungsfehler in physischer Hinsicht erfasst, in die übliche Art und Weise – siehe zum Beispiel Hull und White (2017). Die Intraday-Marktvolatilität kann sehr groß sein und die Transaktionskosten für die Neugewichtung sind, wie bereits erwähnt, sehr niedrig. Daher legen wir die Basisfrequenz der Ergebnistabelle auf alle 8 Stunden fest. Wir passen die 8-stündige Neugewichtung auch an die Finanzierungszeiten des unbefristeten Vertrags an, nämlich 00:00, 08:00 und 16:00 UTC. Dies liegt daran, dass durch die Neugewichtung unter Verwendung unbefristeter Verträge zur Absicherung auch von den Finanzierungszahlungen profitiert werden kann. Anmerkung 17

Mit Ausnahme des HW-Deltas erfordern alle Deltas in (10), dass wir bei der Neugewichtung des Hedge-Portfolios die Steigung der impliziten Volatilitätskurve berechnen. Wir haben verschiedene numerische Techniken zur Berechnung der Ableitung der impliziten Volatilitätskurve untersucht und festgestellt, dass die Anpassung eines kubischen Polynoms der einfachste und genaueste Ansatz ist. Basierend auf den Steigungswerten, die wir numerisch berechnet haben, wenden wir für jede Option, abhängig von ihrer Geldwertigkeit und ihrem Verfallsdatum, (10) an, um das BS-Delta und -Vega unter Verwendung der Standard-BS-Formel zu berechnen. Für das Delta von Hull und White (2017) ahmen wir nicht den 36-monatigen In-Sample-Kalibrierungszeitraum nach, den sie in ihrer empirischen Arbeit zu Aktienindexoptionen verwenden. Für Bitcoin-Optionen stehen nicht einmal 36 Monate nützliche Daten zur Verfügung. Darüber hinaus unterliegen die Bitcoin-Preise einer viel größeren Volatilität als der S&P 500, weshalb wir eine mehrmalige Absicherung pro Tag in Betracht ziehen möchten. Unter Berücksichtigung all dieser Faktoren kalibrieren wir die HW-Delta-Parameter mithilfe von 30 Beobachtungsfenstern mit täglicher Frequenz und 90 Beobachtungsfenstern mit 8-Stunden-Frequenz. Unsere Ergebnisse vergleichen die Absicherungsfehler bei der Verwendung von Futures mit fester Laufzeit und unbefristeten Kontrakten und führen je nach Absicherungsinstrument zwei HW-Regressionen durch.

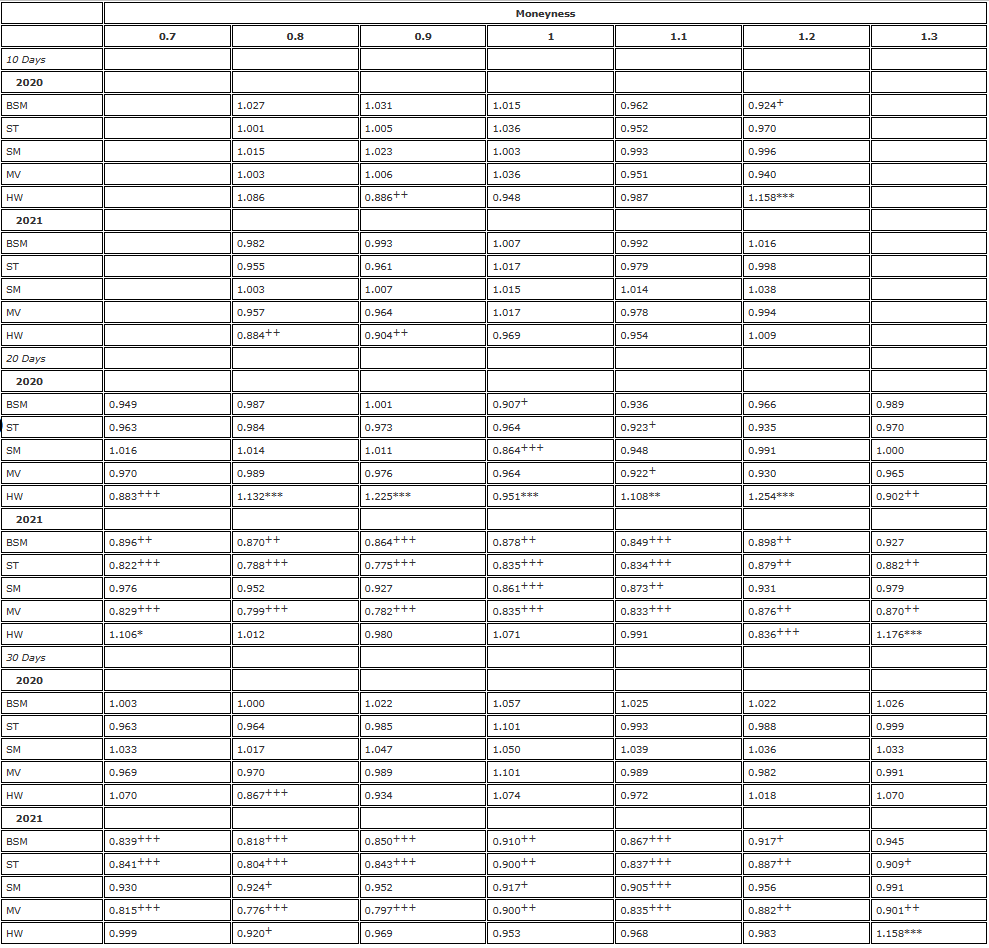
Wir werden unsere Ergebnisse mithilfe eines Standard-F-Tests auf Varianzunterschiede präsentieren und dabei das BS-Delta als Benchmark verwenden, d. h. das Sticky Strike (SS)-Delta aus (10). Zunächst werden in Tabelle 2 die Ergebnisse der Absicherung von 7-Tages-, 1-Tages- und 3-Tages-Optionen mit Währungsgraden zwischen 10,20 und 30,0 dargestellt, wobei jede Option mit den entsprechenden Futures mit fester Laufzeit abgesichert und alle 8 Stunden neu berechnet wird. Gleichgewicht. Bei den Einträgen in der Tabelle handelt es sich um Varianzverhältnisse, d. h. die Varianz der abgesicherten δadj-Fehler im Verhältnis zur Varianz der abgesicherten BS-Delta-Fehler.

Tabelle 2. F-Test-Hedging-Ergebnisse (8-Stunden-Rebalancing, Futures mit festem Verfallsdatum).

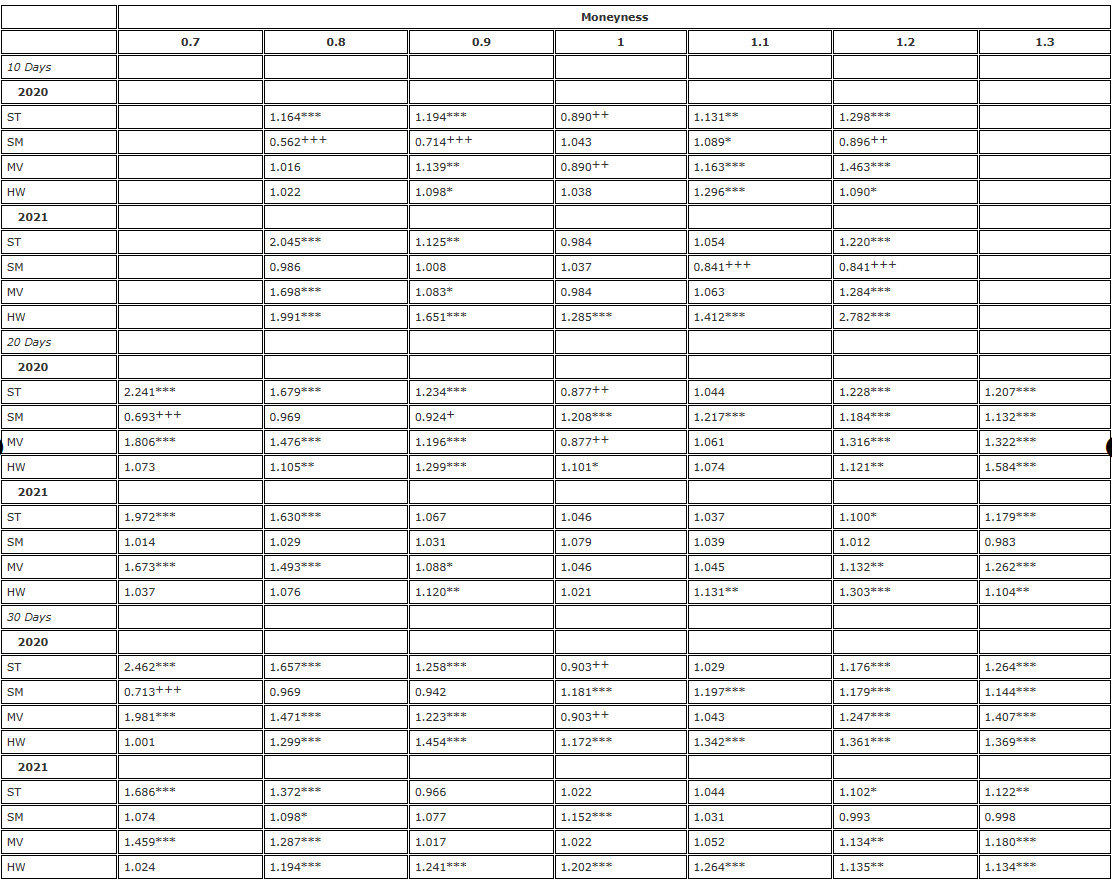
Hinweis: Das Signifikanzniveau des Varianzverhältnisses und des einseitigen F-Tests gelten jeweils für die Nullhypothese 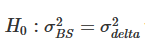und die Alternativhypothese /upload/asset/28dc6465a12c2e427a5ac.png. Die Absicherung basiert auf einem Terminkontrakt mit demselben Verfallsdatum wie die Option und wird alle 8 Stunden neu gewichtet. Wir vergleichen die Varianz der Fehler aus verschiedenen Delta-Hedges im Verhältnis zur Varianz aus der Absicherung mit BS-Delta und teilen die Zweijahresstichprobe in zwei Teile auf. Wir verwendeten Optionen mit drei verschiedenen Laufzeiten und einer Geldmenge von 0,7 bis 1,3, wobei wir OTM-Put-Optionen bei einer Geldmenge <1 und OTM-Call-Optionen bei einer Geldmenge >1 nutzten. Für H∗ werden und verwendet, um die Signifikanzniveaus von 10 %, 5 % bzw. 1 % darzustellen, und das Gleiche gilt für H+.

Je größer die Effektivität der Absicherung, desto geringer die Varianz des Absicherungsfehlers, und der Effizienzgewinn durch die Verwendung des angepassten Smile-Curve-Deltas beträgt 1 minus dieses Varianzverhältnisses. Wenn Sie beispielsweise eine 10-Tage-Option mit einer Geldmenge von 0,8 absichern, ergibt das SM-Delta (Smile Implied) ein Varianzverhältnis von 0,562. Dies bedeutet, dass der Effizienzgewinn im Vergleich zur BS-Delta-Hedging-Methode 1-0,562=43,8 % beträgt, was sehr signifikant ist, weshalb dieser Eintrag mit +++ gekennzeichnet wird. In den Varianzverhältnistabellen geben hochgestellte Ziffern die Signifikanz der Varianzverhältnisse bei den Signifikanzniveaus von 10 %, 5 % und 1 % im einseitigen F-Test an. Zum Beispiel,***Dies deutet darauf hin, dass die Varianz des δadj-Hedging-Fehlers größer ist als die des BS-Delta-Hedging-Fehlers auf dem 1%-Niveau. Und ++ zeigt an, dass die Varianz des δadj-Hedging-Fehlers deutlich kleiner ist als der BS-Delta-Hedging-Fehler auf dem 5%-Niveau.

Betrachten Sie zunächst die Ergebnisse für 2020 in Tabelle 2. Dieser Teil der Stichprobe ist durch langsame, aber stetige Preisanstiege gekennzeichnet, die mit dem stetigen Trendmuster von Derman (1999) übereinstimmen, bei dem wir erwarten würden, dass SS-Delta (BS-Delta) die effektivste Delta-Absicherung darstellt, oder im Fall eines Muster mit begrenzter Reichweite, SM-Delta ist für die Mehrheit der Deltas verantwortlich. Dominanz. Insgesamt zeigen die Ergebnisse für 2020 in Tabelle 2 ein Muster, bei dem der Erfolg eines bestimmten Deltas, das eine BS-Absicherung übertrifft, eher von der Geldmäßigkeit der Option abhängt als von der Laufzeit. Beispielsweise funktioniert ST Delta für At-the-Money-Optionen am besten. Anmerkung 18: Die erzielten Effizienzgewinne reichen von 9,7 % bei der 30-Tage-At-the-Money-Option über 12,3 % bei der 20-Tage-Option bis hin zu 11 % bei der 10-Tage-Option. Die relative Performancerichtung der Smile-Implied-Deltas (d. h. SM-Deltas) im Vergleich zu den ST- und MV-Deltas ist entgegengesetzt, und zwar nicht nur bei At-the-Money-Optionen, sondern auch bei allen In-the-Money-Optionen. Es übertrifft das BS-Delta bei der Absicherung von OTM-Put-Optionen, jedoch nicht bei OTM-Calls (mit Ausnahme des 10-Tage-Calls mit einer Geldmenge von 1,2). Bei der Absicherung von 20-tägigen OTM-Put-Optionen beträgt der Effizienzgewinn unter Verwendung des Smile Implicit (SM)-Deltas im gesamten Jahr 2020 1-0,693 = 30,7 %, was sehr signifikant ist. Bei 30-tägigen OTM-Put-Optionen beträgt der Effizienzgewinn 28,7 %, was nahezu identisch ist. Bei anderen Put-Optionen sind die Effizienzgewinne durch die Verwendung von Smile-Implied Hedging viel geringer und liegen lediglich zwischen 3,1 % und 7,6 %.

Bei allen anderen Optionen liegen jedoch alle angepassten Smile-Deltas unter dem BS-Delta. Dies ist jedoch nicht überraschend, da der Bitcoin-Preis über weite Teile des Jahres 2020 einen stetigen Trend aufwies. Das tatsächliche HW-Hedge-Verhältnis, das von Hull und White (2017) vorgeschlagen wurde, und das Minimum-Varianz-Hedging (MV) von Lee (2001) verbessern das BS-Delta ebenfalls nicht (mit der Ausnahme, dass bei At-the-Money-Optionen das MV-Hedging dasselbe ist wie das ST Absicherung). Ein großer Nachteil von HW Delta besteht darin, dass es zur Schätzung seiner Parameter eine Regression verwendet, was die Annahme einer unabhängigen und identischen Verteilung für einen Vermögenswert wie Bitcoin, der sehr anfällig für Renditesprünge ist, ungültig macht. Die Auswirkungen eines Sprungs bleiben für lange Zeit innerhalb des gleitenden Fensters bestehen und haben daher einen großen Einfluss auf das HW-Absicherungsverhältnis.

Die Abbildungen 2 und 5 zeigen, dass das Jahr 2021 durch höhere Preise, größere Volatilität und einen Anstieg des allgemeinen Volatilitätsniveaus gekennzeichnet war, gepaart mit einer flacheren, aber immer noch asymmetrischen, lächelnden impliziten Volatilitätskurve. Im Laufe des Jahres 2021 schwankte der Bitcoin-Preis stark zwischen 30.000 und fast 70.000 US-Dollar, und wie Abbildung 2 zeigt, wurde die 30-Tage-Smile-Kurve gegen Ende dieses Zeitraums relativ flach. Doch die flache Lächelkurve macht die Schlüsselkomponente des angepassten Deltas, nämlich die Steigung der Lächelkurve, nahezu überflüssig. Es ist daher nicht überraschend, dass im zweiten Jahr unserer Stichprobe alle um die Smiling Curve angepassten Deltas keine signifikante Verbesserung der Standard-BS-Hedge-Ratios für alle 20- und 30-Tage-Optionen ergeben. Im Jahr 2021 wies die sehr kurzfristige 10-Tage-Smile-Kurve jedoch einige seltsame Merkmale auf und zeigte während der Bullenphase des Bitcoin-Preises einen Aufwärtstrend. Aus diesem Grund weist das Smile Implied (SM) Delta-Hedging von 10-tägigen Out-of-the-Money-Call-Optionen eine sehr deutliche Effizienzsteigerung von 15,9 % im Vergleich zur Verwendung von BS Delta auf.

Als nächstes testen die Tabellen 3 und 4 die Robustheit der Ergebnisse in Tabelle 2 auf zwei Arten: zunächst durch erneute Ausführung der Analyse in täglicher Häufigkeit (Tabelle 3) und dann durch Verwendung unbefristeter Verträge anstelle von Futures mit gleicher Laufzeit als Absicherungsinstrument. . Die Ergebnisse in Tabelle 3 zeigen ein ähnliches Muster wie die in Tabelle 2, außer dass sie insgesamt weniger signifikant sind – was uns jedoch nicht überraschen sollte, da es nun nur noch 365 statt 1.095 Beobachtungen pro Jahr gibt. Sie bestätigen unsere Schlussfolgerung aus Tabelle 2, dass kein angepasstes Lächeln-Kurven-Delta das BS-Delta im Jahr 2021 verbessern kann. Im Jahr 2020 haben wir auch das gleiche Leistungsmuster im Verhältnis zum BS-Delta gesehen, d. h. das ST-Delta hat das BS bei ATM-Optionen übertroffen, aber jetzt gibt es einige Hinweise darauf, dass das HW-Delta bei ATM-Optionen und OTM-Put-Optionen besser abschneidet. Es hat auch das BS mit einer Geldigkeit übertroffen von 0,9 – aber keine dieser Varianzverhältnisstatistiken war statistisch signifikant.

Tabelle 3. F-Test-Hedging-Ergebnisse (tägliche Neugewichtung, Futures mit festem Verfallsdatum).

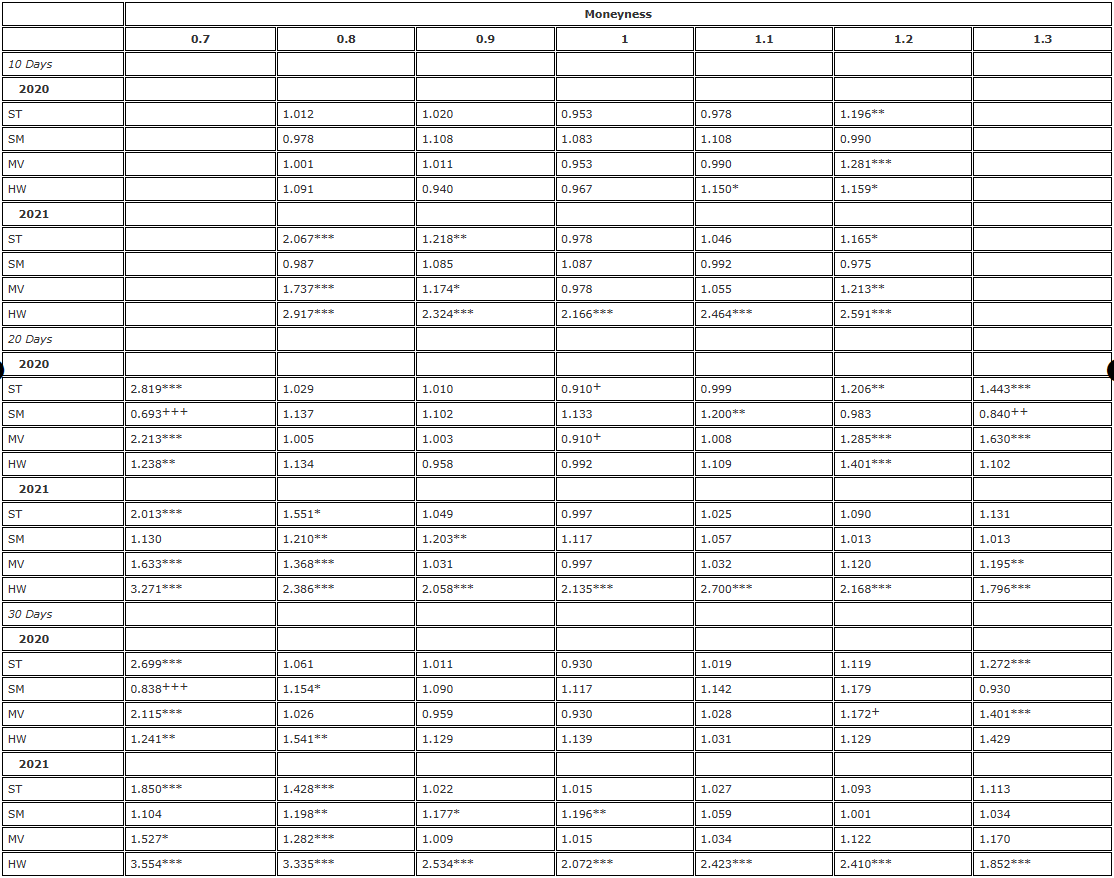
Hinweis: Das Signifikanzniveau des Varianzverhältnisses und des einseitigen F-Tests gelten jeweils für die Nullhypothese 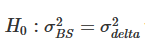und die Alternativhypothese /upload/asset/28dc6465a12c2e427a5ac.png. Die Absicherung basiert auf einem Terminkontrakt mit demselben Verfallsdatum wie die Option und wird alle 8 Stunden neu gewichtet. Wir vergleichen die Varianz der Fehler aus verschiedenen Delta-Hedges im Verhältnis zur Varianz aus der Absicherung mit BS-Delta und teilen die Zweijahresstichprobe in zwei Teile auf. Wir verwendeten Optionen mit drei verschiedenen Laufzeiten und einer Geldmenge von 0,7 bis 1,3, wobei wir OTM-Put-Optionen bei einer Geldmenge <1 und OTM-Call-Optionen bei einer Geldmenge >1 nutzten. Für H∗ werden und verwendet, um die Signifikanzniveaus von 10 %, 5 % bzw. 1 % darzustellen, und das Gleiche gilt für H+.

Tabelle 4. F-Test-Hedging-Ergebnisse (8-Stunden-Rebalancing, unbefristeter Vertrag).

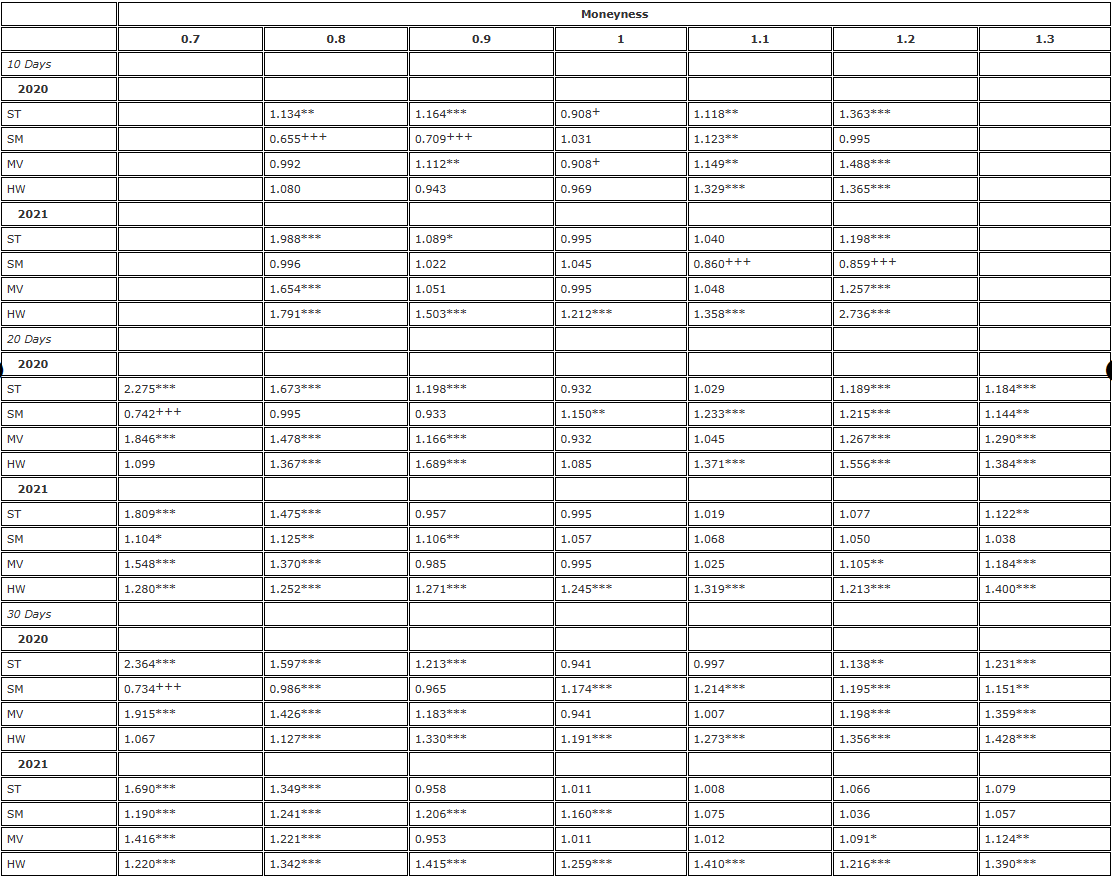
Hinweis: Das Signifikanzniveau des Varianzverhältnisses und des einseitigen F-Tests gelten jeweils für die Nullhypothese 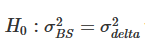und die Alternativhypothese /upload/asset/28dc6465a12c2e427a5ac.png. Die Absicherung basiert auf einem Terminkontrakt mit demselben Verfallsdatum wie die Option und wird alle 8 Stunden neu gewichtet. Wir vergleichen die Varianz der Fehler aus verschiedenen Delta-Hedges im Verhältnis zur Varianz aus der Absicherung mit BS-Delta und teilen die Zweijahresstichprobe in zwei Teile auf. Wir verwendeten Optionen mit drei verschiedenen Laufzeiten und einer Geldmenge von 0,7 bis 1,3, wobei wir OTM-Put-Optionen bei einer Geldmenge <1 und OTM-Call-Optionen bei einer Geldmenge >1 nutzten. Für H∗ werden und verwendet, um die Signifikanzniveaus von 10 %, 5 % bzw. 1 % darzustellen, und das Gleiche gilt für H+.

Tabelle 4 entspricht exakt Tabelle 2. Für die Analyse wird eine Neugewichtungsfrequenz von 8 Stunden verwendet, als Absicherungsinstrumente für alle Optionen werden jedoch unbefristete Verträge verwendet. Wir sehen genau dasselbe Muster der BS-Delta-Underperformance wie in Tabelle 2, mit sehr deutlichen Effizienzgewinnen bei der Absicherung von OTM-Puts unter Verwendung von ST/MV-Deltas mit Smile-Implied-Deltas (d. h. SM-Deltas) und ATM-Optionen. Mit Ausnahme der Smiling Curve Implied (SM) Delta-Absicherung, die erneut einen großen und signifikanten Effizienzgewinn für die Absicherung von 10-tägigen OTM-Call-Optionen lieferte, konnte im Jahr 2021 kein bereinigtes Smiling Curve-Delta das BS-Delta deutlich übertreffen. Bei ATM-Optionen gibt es auch einige kleine ( %) Effizienzgewinne durch die Verwendung des ST/MV-Deltas, und die Varianzverhältnisse in Tabelle 4 sind fast immer kleiner als die in Tabelle 2.

Diese Erkenntnis führt uns zu der Frage: Stellen unbefristete Verträge ein besseres Absicherungsinstrument dar als Futures mit der gleichen Laufzeit wie Optionen? Um diese Frage zu beantworten, betrachten wir das Varianzverhältnis, wobei der Zähler die Varianz des permanenten Hedge-Fehlers und der Nenner die Varianz des Futures-Hedge-Fehlers ist. Wir teilen die Stichprobe erneut in zwei Einjahreszeiträume auf und stellen die Ergebnisse nach Delta (jetzt einschließlich BS-Delta) und Option dar. Tabelle 5 zeigt die Ergebnisse. In der Tabelle bedeutet ein Varianzverhältnis kleiner (größer) 1, dass durch den Einsatz unbefristeter Verträge eine bessere (schlechtere) Absicherungswirkung erzielt werden kann. Die Aussagekraft der F-Statistik hängt davon ab, ob der Perpetual Swap ein besseres (+) oder schlechteres (-) Absicherungsinstrument darstellt als die Futures mit gleicher Laufzeit.*). Es ist klar, dass das Ergebnis fast nicht von der Geldwertigkeit der Option abhängt, sondern vielmehr vom Verfallsdatum der Option und den Marktbedingungen zu diesem Zeitpunkt. Bei 10-Tages-Optionen liegen die OTM-Call-Ratios meist unter 1. Bei 20- und 30-Tage-Optionen könnte es bei der Absicherung mit unbefristeten Optionen insbesondere im Jahr 2021 zu sehr deutlichen Verbesserungen kommen.

Tabelle 5. F-Test zum Vergleich von Futures und unbefristeten Swaps (Neugewichtung alle 8 Stunden).

Hinweis: Das Signifikanzniveau des Varianzverhältnisses und des einseitigen F-Tests gelten jeweils für die Nullhypothese 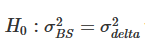und die Alternativhypothese /upload/asset/28dc6465a12c2e427a5ac.png. Die Absicherung basiert auf einem Terminkontrakt mit demselben Verfallsdatum wie die Option und wird alle 8 Stunden neu gewichtet. Wir vergleichen die Varianz der Fehler aus verschiedenen Delta-Hedges im Verhältnis zur Varianz aus der Absicherung mit BS-Delta und teilen die Zweijahresstichprobe in zwei Teile auf. Wir verwendeten Optionen mit drei verschiedenen Laufzeiten und einer Geldmenge von 0,7 bis 1,3, wobei wir OTM-Put-Optionen bei einer Geldmenge <1 und OTM-Call-Optionen bei einer Geldmenge >1 nutzten. Für H∗ werden und verwendet, um die Signifikanzniveaus von 10 %, 5 % bzw. 1 % darzustellen, und das Gleiche gilt für H+.

Obwohl die resultierende Tabelle die relative Gesamteffizienz von Deltas im Hinblick auf verschiedene Anpassungen der Smiling-Curve angibt, deckt unsere Zweijahresstichprobe ein breites Spektrum von Marktregimen ab. Wie in Abbildung 5 dargestellt, schwankt der Bitcoin-Markt schnell zwischen stabilen Trends, Bereichsschwankungen und starken Rückgängen und Anstiegen. Um zu verstehen, welches Delta in welchen Marktzuständen die beste Leistung erbringt, zeigt Abbildung 8 die Zeitreihe des Varianzverhältnisses. Dabei handelt es sich um die Varianz des um die Smiling-Curve bereinigten Delta-Hedge-Fehlers geteilt durch die Varianz des BS-Delta-Hedge-Fehlers. Dadurch wird die Absicherung alle 8 Stunden neu ausbalanciert und jede Varianz wird nun nur unter Verwendung der letzten 90 Beobachtungen berechnet – dasselbe Fenster, das für die Schätzung des HW-Delta-Parameters verwendet wird. Wir betonen, dass Werte größer als 1 eine schlechte Absicherungsleistung des Smile-adjustierten Deltas im Vergleich zum BS-Delta anzeigen. Der Übersichtlichkeit halber stellen wir die Ergebnisse auf einer logarithmischen Skala dar, sodass in diesen Abbildungen ein Varianzverhältnis von 1 durch Null dargestellt wird . . Jede Linie unter Null zeigt an, dass Delta eine Verbesserung gegenüber BS-Delta darstellt, eine Linie über Null zeigt jedoch, dass Delta eine weniger effektive Absicherung bietet als BS.

Abbildung 8. Hedge-Performance der rollierenden Stichprobe. (a) 10-Tage-Optionsergebnisse und (b) 30-Tage-Optionsergebnisse.

Das Varianzverhältnis zeigt, wie sich verschiedene Hedge-Verhältnisse unbefristeter Optionen im Verhältnis zum BS-Delta bei einer 8-stündigen Neugewichtung entwickeln, wobei die Varianz des Hedge-Fehlers anhand der ersten 90 Beobachtungen berechnet wird. Wir präsentieren die Log-Ergebnisse für (a) 10-Tage- und (b) 30-Tage-Optionen über eine zweijährige Stichprobe. Die durchgezogene Linie 0 ist ein Referenzwert, ein Verhältnis größer als 0 zeigt eine schlechtere Leistung im Vergleich zu BS an und ein Verhältnis kleiner als 0 zeigt eine bessere Leistung im Vergleich zu BS an. Die Abbildung (a) oben zeigt die Performance einer OTM-Put-Option mit m=0,8, während das obere Diagramm in (b) die Performance einer OTM-Put-Option mit m=0,7 zeigt. Das mittlere Diagramm zeigt die Performance von (a) und (b). Die Performance von ATM-Optionen wird unten für OTM-Call-Optionen mit (a) Moneyness von 1,2 und (b) Moneyness von 1,3 angezeigt.

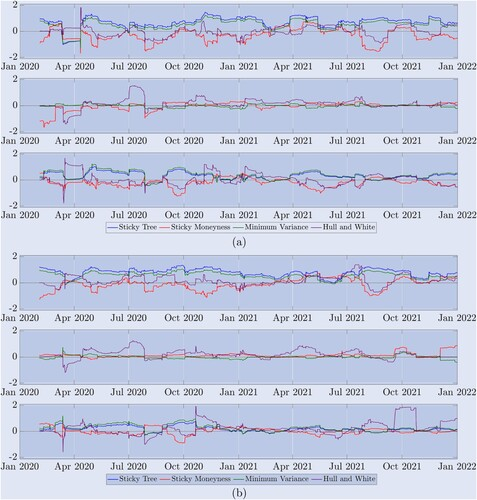
Die oberen drei Diagramme (a) zeigen die Ergebnisse für 10-Tage-Optionen und die unteren drei Diagramme (b) zeigen die Ergebnisse für 30-Tage-Optionen. In den Fällen (a) und (b) handelt es sich bei den obigen Grafiken jeweils um OTM-Put-Optionen. Diese Grafiken bestätigen die Ergebnisse aus Tabelle 2: Die Deltas von ST (blau) und MV (grün) schnitten fast über den gesamten Zeitraum schlechter ab. sind niedriger als BS; gemäß Dermans (1999) Marktklassifizierungserwartungen übertrifft das SM-Delta das BS-Delta in Zeiträumen, in denen der Markt in einer Spanne gefangen ist, aber wenn der Markt im Trend liegt, wie z. B. in der ersten Periode, die im Januar 2021 beginnt, Während der zweiten Bullenlauf und dem zweiten Bullenlauf später im selben Jahr schnitt SM Delta nicht so gut ab wie BS Delta, während HW Delta eine andere Leistung zeigte. Das mittlere Diagramm in jedem Diagrammsatz zeigt das Varianzverhältnis für die abgesicherten ATM-Optionen. In diesem Fall sind alle Smile-bereinigten Deltas sehr ähnlich, da die Smile-Kurve von Bitcoin an diesem Punkt normalerweise (aber nicht immer) sehr flach ist. Das untere Diagramm in jedem Diagrammsatz zeigt die Performance verschiedener Deltas zur Absicherung von OTM-Call-Optionen. Auch hier scheint SM Delta die beste Option zu sein, ist aber nur für 10-Tage-Optionen verfügbar und stellt gegenüber BS keine so große Verbesserung dar wie der OTM-Put. Bei 30-Tage-Optionen konnte kein Delta die BS kontinuierlich verbessern, insbesondere im Jahr 2021.

7. Fazit

Frühere akademische empirische Studien haben sich lediglich mit der Delta-Hedging-Methode befasst, bei der die implizite modellfreie Smiling Curve und die für Aktienindexoptionen adjustierte institutionenabhängige Smiling Curve zum Einsatz kamen. Auch wenn die Ergebnisse gemischt sind, lässt sich allgemein schlussfolgern, dass ein an die Smiling Curve angepasstes Hedge-Ratio die Performance des Black-Scholes-Deltas für Out-of-the-Money-Put-Optionen nur unter bestimmten Umständen verbessern kann. Wir haben jedoch gezeigt, dass sich die Smiley-Kurve der impliziten Volatilität von Bitcoin ganz anders verhält als Aktienindexoptionen. Daher ist es sehr interessant, die Wirksamkeit des von Praktikern normalerweise bevorzugten, an die Smile-Kurve angepassten Hedge-Ratios zu untersuchen.

Wir empfehlen die Verwendung verschiedener potenzieller Verwendungen des angepassten Deltas, von denen die meisten ausschließlich auf der Beziehung zwischen der impliziten Volatilität der Hedge-Option und der Steigung der Smiley-Kurve der impliziten Volatilität zum Verfallszeitpunkt beruhen. Durch die Verwendung eines einzigartigen Datensatzes zu Deribit-Optionen sind wir in der Lage, die Absicherungsperformance der aktivsten Bitcoin-Optionen an der Deribit-Börse zu vergleichen, d. h. Optionen mit Ausübungspreisen 30 % über und unter dem aktuellen BTC-Index und Verfallszeiten von bis zu einem Monat. Wir analysieren die Varianz von Delta-Hedging-Fehlern, wobei das Hedging-Instrument ein Futures-Kontrakt mit demselben Verfallsdatum wie die Option oder ein unbefristeter Kontrakt sein kann – ein innovatives Produkt, das es nur auf dem Markt für Kryptowährungs-Derivate gibt. Wenn wir die Absicherung alle acht Stunden (zeitgleich mit der Finanzierungszeit des unbefristeten Vertrags) oder täglich neu gewichten und Terminkontrakte oder unbefristete Verträge mit derselben Ablaufzeit wie das Absicherungsinstrument verwenden, erhalten wir einige sehr robuste Ergebnisse. Anstatt einfach die mittleren quadrierten Fehler verschiedener Hedge-Verhältnisse zu tabellieren, wie es Coleman et al. (2001), Vähämaa (2004), Alexander et al. (2012) und viele andere getan haben, wenden wir einen einfachen Varianzverhältnistest an. das die statistische Signifikanz des Effizienzgewinns durch die Verwendung eines bestimmten Deltas im Verhältnis zum BS-Delta angibt.

Mit diesem Ansatz zeigen wir, dass für Out-of-the-Money-Optionen das aus der Smiling Curve implizierte Delta (Sticky Moneyness) bei der Absicherung deutlich besser ist als das Standard-Delta von Black-Scholes, in manchen Fällen sogar um mehr als 40 % effizienter. . Das Minimum-Varianz-Delta übertrifft das BS-Delta ebenfalls, allerdings nur bei In-the-Money-Optionen, da es mit dem Sticky-Tree-Delta zusammenfällt. Kein anderes an die Smiling-Kurve angepasstes Delta hat das BS-Delta durchweg verbessert, und selbst Smile-Implizit- und Minimum-Varianz-Delta-Hedges zeigten während des Großteils des Jahres 2021 eine schlechte Performance. Die einzige Ausnahme ist der implizite Smile-Hedge für Out-of-the-Money-Call-Optionen mit kurzer Laufzeit, wenn die Steigung der impliziten Volatilitätskurve positiv wird. Im Vergleich zu Aktienindizes wie dem S&P 500 schwanken die Bitcoin-Preise nicht gleichmäßig nach oben und stürzen dann plötzlich ab - ihre Preisanstiege können genauso groß sein wie ihre Preisrückgänge, sodass ihre Smile-Kurve sehr symmetrisch sein oder sogar vollständig nach oben kippen kann . Wir zeigen auch, dass unbefristete Kontrakte bessere Absicherungsinstrumente sind als Futures mit der gleichen Laufzeit wie die Optionen, unabhängig von der Geldwertigkeit der Optionen. Dies zeigt sich insbesondere bei Optionen mit längerer Laufzeit, bei denen die Basis zwischen unbefristeten Kontrakten und Futures am größten ist.

Der Schwerpunkt unserer Forschung liegt auf robusten modellfreien Frameworks, die auch die bevorzugte Wahl vieler Praktiker sind. Eine Absicherung mittels parametrischer stochastischer und/oder lokaler Volatilitätsmodelle ziehen wir nicht in Betracht, und zwar aus dem einfachen Grund, dass das Delta aufgrund der Skaleninvarianz dieser Prozesse praktisch modellfrei ist und daher mit dem in dieser Studie verwendeten, aus dem Smile-Impliziten verwendeten Delta übereinstimmt. Da wir in unserer Studie das robuste minimale Varianzdelta von Lee (2001) einführen, glauben wir, dass das Hinzufügen verschiedener stochastischer Volatilitätsprozesse für die dynamische Delta-Absicherung eine weniger relevante Forschungsfrage für die aktuelle Kryptohandelsbranche ist.

Dieser Artikel konzentriert sich auf dynamisches Delta-Hedging mit häufigem Rebalancing, das Market Makern bei Bitcoin-Optionen dabei helfen kann, einen Wettbewerbsvorteil auf einem Markt zu erlangen, der erst im Jahr 2021 wirklich zu reifen beginnt. Der Bitcoin-Markt ist jedoch so schnell gewachsen, dass große professionelle Händler wie Jump Trading, Jane Street, XBTO und Cumberland DRW mit Bitcoin-Optionen handeln, oft mit täglichen Volumina von über 1 Milliarde US-Dollar. Um der Nachfrage gerecht zu werden, werden außerdem viele neue Verfallsoptionen und Optionskontraktgrößen eingeführt. So hat die CME beispielsweise vor Kurzem Mikro-Bitcoin-Optionen für Privathändler auf den Markt gebracht. Trotzdem ist die Geld-Brief-Spanne bei Bitcoin-Optionen immer noch relativ groß und viel höher als bei Bitcoin-Futures oder unbefristeten Kontrakten. Daher hängt die Rentabilität des Market Making im Bitcoin-Optionsmarkt stärker von einer genauen dynamischen Delta-Absicherung ab als von einer Delta-Gamma-Vega-Absicherung. Wenn die Geld-Brief-Spanne von Bitcoin-Optionen in Zukunft abnimmt, könnte es interessant sein, die Gamma- und Vega-Absicherung des Bitcoin-Optionsbuchs zu untersuchen. Zum Zeitpunkt der Abfassung dieses Artikels können jedoch die Transaktionskosten für den Einsatz von Optionen zur Absicherung von Preis- und Volatilitätsrisiken alle zusätzlichen Gewinne aufzehren, die durch niedrigere Spreads erzielt werden könnten.

Stellungnahme

Wir danken den anonymen Gutachtern, deren Kommentare das Papier deutlich verbessert haben.

Offenlegungserklärung

Die Autoren erklären, dass keine Interessenkonflikte vorliegen.

Hinweise

1. Im Gegensatz dazu sind Deltas, die aus nicht-skaleninvarianten Modellen abgeleitet werden, wie etwa dem lokalen Volatilitätsmodell von Dupire (1994) oder dem Sticky-Tree-Modell von Derman und Kани (1994), theoretisch nicht gleichwertig mit skaleninvarianten Deltas. Das Delta der minimalen Varianz ist ebenfalls kein skaleninvariantes Delta, sondern die Gesamtableitung, die den Vega-Effekt aus von Null verschiedenen Preisvolatilitätskorrelationen beinhaltet.

2. Siehe beispielsweise die jüngsteCAIA Artikel, ein weiterer Artikel auf MediumArtikel,sowie risklatte Und stackexchange Und mehrere Foren zum Thema quantitative Finanzwissenschaft.

3. In dieser Literatur kalibrieren Nastasi et al. (2020) ein Smile-Konsistenzmodell für Rohstoffoptionen, um die Smile-Dynamik zu erfassen, während Malz (2000) erklärt, wie Smile-Anpassungen bei der Messung des Risikos von Devisenoptionen berücksichtigt werden können. Im Inneren.

4. Deribit-Optionen haben eine zweitägige, zweiwöchentliche, zweimonatliche und vierteljährliche Verfallszeit und können eine Laufzeit von bis zu 9 oder 12 Monaten haben. Sein Basiswert ist der „Deribit BTC Index“ (BTC), ein gleichgewichteter Durchschnitt der letzten Bitcoin-Preise an 11 Börsen, ausgenommen der höchsten und niedrigsten Preise. Die verbleibenden 9 Preise werden zur Berechnung des Index verwendet. Zu diesen Börsen gehören derzeit Binance, Bitfinex, Bitstamp, Bittrex, Coinbase Pro, Gemini, Huobi Global, Itbit, Kraken, LMAX Digital und OKEx, und der Index wird jede Sekunde aktualisiert. Es gibt mehr Verfallsdaten für Optionen als Verfallsdaten für Futures. Damit Deribit Optionspreise sowohl für Bitcoin als auch für USD auflisten kann, verwendet das Unternehmen daher dieselben (möglicherweise synthetischen) Futures-Preise als Verfallsdaten für die Optionen. Dies bedeutet nicht, dass der (ggf. synthetische) Terminkontrakt der Basiswert ist. Tatsächlich,Deribit’s Optionsspezifikationen Es wird klar angegeben, dass der Basiswert der Deribit BTC Index ist. Bei kurzfristigeren Optionen liegt die Ausübungsspanne zwischen 50 % und 150 % des aktuellen BTC-Preises, und bei Optionen mit Laufzeiten von mehr als 6 Monaten kann die Ausübungsspanne bis zu 800 % des aktuellen BTC-Preises betragen.

5. Siehe auchHistorische Optionsdaten der CBOE, um das Handelsvolumen von SPX-Optionen auf CBOE zu verstehen.

6. Siehe auchHandelsvolumen für Bitcoin-OptionenUnd Goldman Sachs Bitcoin-Optionen。

7. Als nächstes folgt CME (5%), dann OKEx (2,5%) sowie FTX und Bit.com. Weitere Einzelheiten finden Sie unterThe Block Options。

8. Zur Berechnung der endgültigen Rendite verwendet Deribit den durchschnittlichen BTC-Index 30 Minuten vor Ablauf als Abrechnungswert. Einzelheiten finden Sie im offiziellenDeribit’s Optionsspezifikationen . Es ist wichtig zu beachten, dass der Deribit Bitcoin-Optionsmarkt nicht vollständig ist. Die Indizes selbst sind nicht handelbar und erfordern eine teure Replikation und häufige Neugewichtung. Für Händler ist der Markt unvollständig, da Informationen zur genauen Berechnung des Abrechnungswerts fehlen. Eine detaillierte Diskussion dieses Themas geht jedoch über den Rahmen dieses Dokuments hinaus, und wir verweisen für eine eingehende Diskussion auf Alexander et al. (2022a).

9. Bitte beziehen Sie sich auf 2022Dezentraler Kryptowährungsmarkt Rang.

10. Inverse Futures sind auf Bitcoin lautende Terminkontrakte, die auf dem USD-Preis von Bitcoin oder dem Wert eines Bitcoin-Index basieren. Sowohl Standard- als auch inverse Futures verwenden den USD-Wert als Basiswert, unterscheiden sich jedoch in der Abwicklungsmethode: Die Standard-Futures der CME haben einen Nominalbetrag von 0,1 oder 5 Bitcoins und werden in USD bezahlt, während der Nominalbetrag der inversen Futures 1 USD oder 10 USD beträgt. und zahlbar in Bitcoin. Andererseits führt dieser Zahlungsmechanismus zu einer anderen Gewinn- und Verlustberechnung (PnL). Bei Standard-Futures müssen Sie den Schlusskurs vom Eröffnungskurs des Futures abziehen und das Ergebnis mit dem Nominalbetrag multiplizieren, um den Gewinn oder Verlust in US-Dollar zu ermitteln. Für inverse Futures (und Optionen) gilt ein anderes Abwicklungsverfahren: Dabei wird der Kehrwert des Eröffnungskurses vom Kehrwert des Schlusskurses abgezogen und das Ergebnis dann mit dem Nominalwert der Position multipliziert, um den in Bitcoin gemessenen Gewinn oder Verlust zu ermitteln. Der „Eröffnungspreis“ und der „Schlusspreis“ beziehen sich hier auf den Dollarwert des Terminkontrakts zum Zeitpunkt des Eingehens und Verlassens der Position.

11. Siehe auchDeribit-Dauerfinanzierungssatz, für eine Beschreibung der Berechnung des Finanzierungssatzes von Deribit.

12. Siehe auchThe BlockoderCoinglass. Es ist wichtig anzumerken, dass mehr als acht Börsen ungewöhnlich hohe Handelsvolumina aufwiesen. Dabei haben wir jedoch die vielen Börsen übersehen, die aufgrund von Wash-Trading ihre Volumina künstlich aufgebläht haben.

13. Diese Näherung wurde auch von Coleman et al. (2001) und vielen anderen befürwortet.

14. Derman (1999) bezeichnete das SS-Modell als „Versuch eines armen Mannes“, das BS-Modell mithilfe eines impliziten Volatilitätsbaums zu replizieren.

15. Mit Ausnahme von Puts (m = 0,7) und Calls (m = 1,3), die sehr weit aus dem Geld liegen, werden diese Optionen in der Kategorie der kurzfristigen Verfallsoptionen unterbewertet. Da wir nur in 75 % der Fälle synthetische Preise berechnen konnten, haben wir diese Optionen aus unseren Endergebnissen ausgeschlossen.

16. Natürlich ist der PCP-Wert für jedes Trainingsniveau unterschiedlich. Da sich der Handel normalerweise auf ATM-Optionen konzentriert, ist es schwierig, einen ITM/OTM-Ausübungspreis zu finden, bei dem sowohl Calls als auch Puts aktiv gehandelt werden. Daher verwenden wir den PCP-Wert, der aus der Rückberechnung von ATM-Optionen abgeleitet wird. Wir interpolieren die ATM-PCP-Werte für zwei benachbarte Verfallsdaten und verwenden diese Werte, um bei Bedarf synthetische feste Optionspreise zu erhalten.

17. Da wir beispielsweise in unserer Konstruktion immer einen unbefristeten Vertrag halten, muss der Hedger eine Finanzierung zahlen, wenn die Basis des unbefristeten Vertrags positiv ist, und erhält eine Finanzierung, wenn die Basis negativ ist. Für die Absicherung von Long-Optionspositionen gilt das Gegenteil. Abbildung 7 zeigt auf jeden Fall, dass sich die Grundlage des unbefristeten Vertrags ändert, mal positiv, mal negativ. Es ist nicht schwierig, einen Absicherungsalgorithmus zu schreiben, um eine abgesicherte Position vollständig zu verlassen, bevor die Finanzierung abläuft. Dieser Algorithmus wird jedoch nicht beendet, wenn die abgesicherte Position eine Finanzierung erhält. Diese Art von „Finanzierungsgebührenstrategie“ ist heutzutage bei Hedgefonds sehr verbreitet, und zwar auf Märkten, auf denen es keine Regulierungen gibt, die den Betrieb solcher strategischer Trading-Bots verhindern. In jedem Fall empfehlen wir lediglich, den Absicherungsstrategien Finanzierungsstrategien hinzuzufügen, und untersuchen nicht potenzielle Gewinne oder Verluste, da dies keine Studie zu Hochfrequenzhandelsstrategien ist.

18. Bei ATM-Optionen sind die ST- und MV-Deltas identisch und daher sind die Ergebnisse dieselben, aber nur in diesem Fall.

Verweise

1. Alexander, C., Pricing, Hedging and Trading Financial Instruments. Market Risk Analysis III, 2008 (Wiley). [Google Scholar]

2. Alexander, C. and Nogueira, L., Model-free hedge ratios and scale invariant models. J. Bank. Finance, 2007a, 31, 1839–1861. [Crossref], [Web of Science ®], [Google Scholar]

3. Alexander, C. and Nogueira, L., Model-free price hedge ratios for homogeneous claims on tradable assets. Quant. Finance, 2007b, 7(5), 473–479. [Taylor & Francis Online], [Web of Science ®], [Google Scholar]

4. Alexander, C., Rubinov, A., Kalepky, M. and Leontsinis, S., Regime-dependent smile-adjusted delta hedging. J. Futures Mark., 2012, 32(3), 203–229. [Crossref], [Web of Science ®], [Google Scholar]

5. Alexander, C., Chen, D. and Imeraj, A., Inverse and quanto inverse options in a Black–Scholes world. SSRN Working Paper, 2022a. [Crossref], [Google Scholar]

6. Alexander, C., Deng, J., Feng, J. and Wan, H., Net buying pressure and the information in bitcoin option trades. J. Financ. Mark., 2022b. (Article in Press). [Crossref], [Google Scholar]

7. Attie, L., The performance of smile-implied delta hedging. Canadian Derivatives Institute, Technical Note TN 17-01, 2017. [Google Scholar]

8. Bakshi, G., Cao, C. and Chen, Z., Empirical performance of alternative option pricing models. J. Finance, 1997, 52, 2003–2049. [Crossref], [Web of Science ®], [Google Scholar]

9. Bates, D., Hedging the smirk. Finance Res. Lett., 2005, 2(4), 195–200. [Crossref], [Google Scholar]

10. Bl