Ein leistungsstarkes Werkzeug für programmatische Trader: Inkrementeller Aktualisierungsalgorithmus zur Berechnung von Mittelwert und Varianz

Einleitung

Bei programmatischem Handel ist es oft notwendig, Durchschnitte und Varianzen zu berechnen, wie z.B. die Berechnung von gleitenden Durchschnitten und Volatilitätsindikatoren. Wenn wir hochaufwendige und langfristige Berechnungen benötigen, ist es notwendig, historische Daten lange Zeit zu speichern, was sowohl unnötig als auch ressourcenanwendend ist. Dieser Artikel stellt einen Online-Aktualisierungsalgorithmus zur Berechnung von gewichteten Durchschnitten und Varianzen vor, der besonders wichtig für die Verarbeitung von Echtzeitdatenströmen und die dynamische Anpassung von Handelsstrategien, insbesondere Hochfrequenzstrategien, ist. Der Artikel enthält auch die entsprechende Python-Code-Implementierung, um Händlern zu helfen, den Algorithmus schnell zu implementieren und im tatsächlichen Handel anzuwenden.

Einfacher Durchschnitt und Varianz

Wenn wir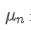um den durchschnittlichen Wert des n-ten Datenpunktes darzustellen, unter der Annahme, dass wir bereits den Durchschnitt von n-1 Datenpunkten /upload/asset/28e28ae0beba5e8a810a6.png berechnet haben, erhalten wir jetzt einen neuen Datenpunkt /upload/asset/28d4723cf4cab1cf78f50.png. Wir wollen die neue durchschnittliche Zahl berechnen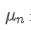Die folgenden Daten sind eine detaillierte Ableitung.

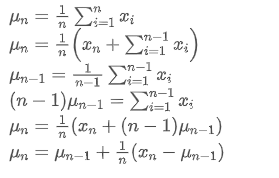
Der Prozess der Aktualisierung der Varianz kann in folgende Schritte unterteilt werden:

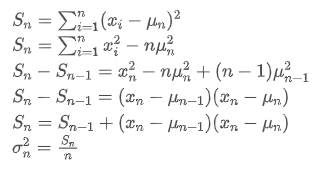
Wie aus den beiden obigen Formeln hervorgeht, ermöglicht uns dieser Prozeß, bei jedem neuen Datenpunkt neue Durchschnitte und Varianzen zu aktualisieren.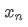Das Problem besteht jedoch darin, dass wir auf diese Weise den Mittelwert und die Varianz aller Proben berechnen, während wir in tatsächlichen Strategien einen bestimmten festen Zeitraum berücksichtigen müssen. Die Beobachtung der obigen Durchschnittsaktualisierung zeigt, dass die Menge der neuen Durchschnittsaktualisierungen eine Abweichung zwischen neuen Daten und vergangenen Durchschnittswerten multipliziert mit einem Verhältnis ist. Wenn dieses Verhältnis fixiert ist, führt dies zu einem exponentiell gewichteten Durchschnitt, über den wir als nächstes sprechen werden.

Exponentiell gewichteter Mittelwert

Der exponentielle gewichtete Durchschnitt kann durch folgende rekursive Beziehung definiert werden:

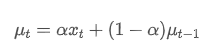
Unter ihnen: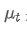ist der exponentielle gewichtete Durchschnitt zum Zeitpunkt t,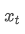ist der beobachtete Wert zum Zeitpunkt t, α ist der Gewichtsfaktor und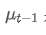ist der exponentiell gewichtete Durchschnitt des vorherigen Zeitpunkts.

Exponentiell gewichtete Varianz

Was die Varianz betrifft, müssen wir den exponentiell gewichteten Durchschnitt der Quadratdeviationen an jedem Zeitpunkt berechnen.

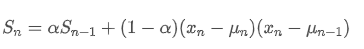
Unter ihnen: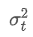ist die exponentiell gewichtete Varianz zum Zeitpunkt t und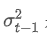ist die exponentiell gewichtete Varianz des vorherigen Zeitpunkts.

Beobachten Sie den exponentiell gewichteten Durchschnitt und die Varianz, ihre inkrementellen Aktualisierungen sind intuitiv, behalten einen Teil der vergangenen Werte und fügen neue Änderungen hinzu.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA und EMA

Der SMA (auch als arithmetisches Mittel bekannt) und der EMA sind zwei gemeinsame statistische Maßnahmen, die jeweils unterschiedliche Eigenschaften und Verwendungen aufweisen. Der erste weist jeder Beobachtung ein gleiches Gewicht zu, was die zentrale Position des Datensatzes widerspiegelt. Der zweite ist eine rekursive Berechnungsmethode, die neueren Beobachtungen ein höheres Gewicht verleiht. Die Gewichte sinken exponentiell, wenn der Abstand zur aktuellen Zeit für jede Beobachtung zunimmt.

• Gewichtsverteilung: Die SMA legt jedem Datenpunkt das gleiche Gewicht zu, während die EMA den jüngsten Datenpunkten ein höheres Gewicht verleiht.
• Empfindlichkeit gegenüber neuen Informationen: Der SMA ist nicht empfindlich genug für neu hinzugefügte Daten, da er alle Datenpunkte neu berechnen muss.
• Rechenkomplexität: Die Berechnung der SMA ist relativ einfach, aber mit zunehmender Anzahl von Datenpunkten steigen auch die Rechenkosten.

Umrechnungsmethode zwischen EMA und SMA

Obwohl SMA und EMA konzeptionell unterschiedlich sind, können wir die EMA annähernd einer SMA mit einer bestimmten Anzahl von Beobachtungen annähern, indem wir einen geeigneten α-Wert wählen.

Der SMA ist der arithmetische Durchschnitt aller Preise innerhalb eines bestimmten Zeitfensters. Für ein Zeitfenster N kann der Mittelpunkt des SMA (d. h. die Position, in der sich die durchschnittliche Zahl befindet) als:

das Zentroid der SMA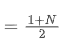

EMA ist eine Art gewichteter Durchschnitt, bei dem die neuesten Datenpunkte ein größeres Gewicht haben. Das Gewicht der EMA nimmt im Laufe der Zeit exponentiell ab.

der Mittelpunkt der EMA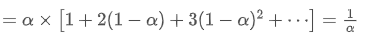

Wenn wir davon ausgehen, dass SMA und EMA denselben Zentroid haben, erhalten wir:

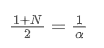
Um diese Gleichung zu lösen, können wir die Beziehung zwischen α und N erhalten.

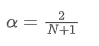
Dies bedeutet, dass für einen bestimmten SMA von N Tagen der entsprechende α-Wert verwendet werden kann, um eine äquivalente EMA zu berechnen, so dass sie den gleichen Mittelpunkt haben und die Ergebnisse sehr ähnlich sind.

Umwandlung der EMA mit unterschiedlichen Aktualisierungsfrequenzen

Angenommen, wir haben eine EMA, die sich jede Sekunde aktualisiert, mit einem Gewichtsfaktor von /upload/asset/28da19ef219cae323a32f.png. Dies bedeutet, dass jede Sekunde ein neuer Datenpunkt mit einem Gewicht von /upload/asset/28da19ef219cae323a32f.png der EMA hinzugefügt wird, während der Einfluss alter Datenpunkte mit /upload/asset/28cfb008ac438a12e1127.png multipliziert wird.

Wenn wir die Aktualisierungsfrequenz ändern, z. B. einmal alle f Sekunden, möchten wir einen neuen Gewichtsfaktor /upload/asset/28d2d28762e349a03c531.png finden, so dass die Gesamtwirkung von Datenpunkten innerhalb von f Sekunden die gleiche ist wie bei Aktualisierung jede Sekunde.

Innerhalb von f Sekunden, wenn keine Aktualisierungen vorgenommen werden, wird die Wirkung alter Datenpunkte kontinuierlich f mal abnehmen, jedes Mal multipliziert mit /upload/asset/28e50eb9c37d5626d6691.png. Daher beträgt der Gesamtzerfallfaktor nach f Sekunden /upload/asset/28e296f97d8c8344a2ee6.png.

Damit die EMA, die alle f Sekunden aktualisiert wird, den gleichen Zerfallseffekt hat wie die EMA, die jede Sekunde innerhalb eines Aktualisierungszeitraums aktualisiert wird, setzen wir den Gesamtzerfallsfaktor nach f Sekunden gleich dem Zerfallsfaktor innerhalb eines Aktualisierungszeitraums:

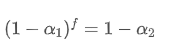
Wenn wir diese Gleichung lösen, erhalten wir neue Gewichtsfaktoren.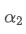

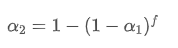
Diese Formel liefert den ungefähren Wert des neuen Gewichtsfaktors /upload/asset/28d2d28762e349a03c531.png, der den EMA-Gleichungseffekt bei Änderungen der Updatefrequenz unverändert hält.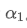mit einem Wert von 0,001 und aktualisiert ihn alle 10 Sekunden, wenn er jede Sekunde auf eine Aktualisierung geändert wird, den entsprechenden Wert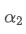wäre ungefähr 0,01.

Implementierung von Python-Code

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Zusammenfassung

Im hochfrequenten programmatischen Handel ist die schnelle Verarbeitung von Echtzeitdaten entscheidend. Um die Rechenleistung zu verbessern und den Ressourcenverbrauch zu reduzieren, stellt dieser Artikel einen Online-Update-Algorithmus zur kontinuierlichen Berechnung des gewichteten Durchschnitts und der Varianz eines Datenstroms vor. Echtzeit-Inkrementelle Updates können auch für verschiedene statistische Daten und Indikatorberechnungen verwendet werden, wie die Korrelation zwischen zwei Vermögenswertpreisen, lineare Anpassung usw., mit großem Potenzial. Die Inkrementelle Aktualisierung behandelt Daten als Signalsystem, was eine Evolution des Denkens im Vergleich zu Festzeitberechnungen ist.