Messen von Risiko und Rendite - Einführung in die Markowitz-Theorie

Letzte Woche, als ichWie man Positionsrisiken misst - Einführung in die VaR-MethodeIn diesem Artikel wurde erwähnt, dass das Risiko eines Portfolios nicht den Risiken einzelner Vermögenswerte entspricht und mit ihrer Preiskorrelation zusammenhängt. Nehmen wir zwei Vermögenswerte als Beispiel, wenn ihre positive Korrelation sehr stark ist, d.h. sie steigen und fallen zusammen, dann werden diversifizierte Investitionen das Risiko nicht reduzieren. Wenn es eine starke negative Korrelation gibt, können diversifizierte Investitionen das Risiko erheblich reduzieren. Die natürliche Frage stellt sich dann: Wie maximieren wir die Rendite bei einem bestimmten Risiko, wenn wir in ein Portfolio investieren? Dies führt uns zur Markowitz-Theorie, die wir heute vorstellen werden.

Die moderne Portfoliotheorie (MPT), die 1952 von Harry Markowitz vorgeschlagen wurde, ist ein mathematischer Rahmen für die Portfolienauswahl. Sie zielt darauf ab, die erwarteten Renditen zu maximieren, indem verschiedene Kombinationen von Risikoanlagen ausgewählt und gleichzeitig das Risiko kontrolliert wird. Die Kernidee ist, dass sich die Preise von Vermögenswerten nicht vollständig synchron miteinander bewegen (d. h. es gibt eine unvollständige Korrelation zwischen Vermögenswerten) und das Gesamtinvestitionsrisiko durch diversifizierte Vermögensallokation reduziert werden kann.

Das Schlüsselkonzept der Markowitz-Theorie

1. Erwartete Rendite: Dies ist die Rendite, die Anleger erwarten, aus dem Besitz von Vermögenswerten oder einem Anlageportfolio zu erhalten, die in der Regel auf der Grundlage historischer Renditendaten prognostiziert wird.

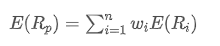
Wo?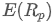ist die erwartete Rendite des Portfolios,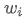ist das Gewicht des i-ten Vermögenswerts im Portfolio,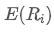ist die erwartete Rendite des i-ten Vermögenswerts.

2. Risikopositionen, für die keine Risikopositionen gelten: Verwendet zur Messung der Unsicherheit der Anlageerträge oder der Volatilität von Anlagen.

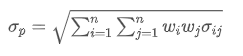
Wo?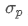stellt das Gesamtrisiko des Portfolios dar,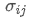ist die Kovarianz von Vermögenswert i und Vermögenswert j, die die Preisänderungsbeziehung zwischen diesen beiden Vermögenswerten misst.

3. Kovarianz: Messen der Wechselbeziehung zwischen den Preisänderungen zweier Vermögenswerte.

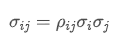
Wo?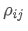ist der Korrelationskoeffizient von Vermögenswert i und Vermögenswert j,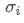und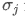sind die Standardabweichungen von Vermögenswert i bzw. von Vermögenswert j.

4. Effiziente Grenze: Im Koordinatensystem Risiko-Rendite ist die effiziente Grenze die Anzahl der Anlageportfolios, die bei einem gegebenen Risikoniveau die maximal erwartete Rendite erzielen können.

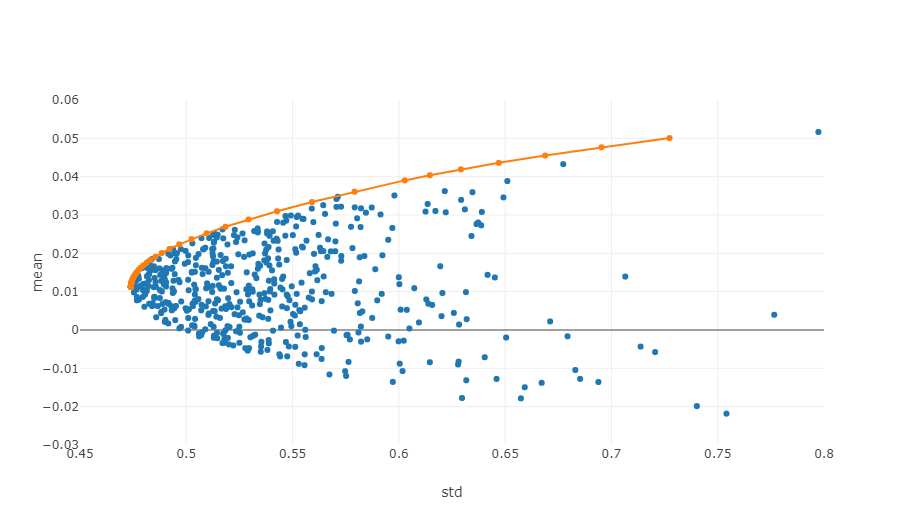
Das obige Diagramm ist eine Illustration einer effizienten Grenze, bei der jeder Punkt ein anderes gewichtetes Anlageportfolio darstellt. Die X-Achse bezeichnet Volatilität, die dem Risikoniveau entspricht, während die Y-Achse die Rendite darstellt. Unser Fokus liegt eindeutig auf dem oberen Rand des Diagramms, da es die höchsten Renditen bei gleichwertigen Risikoniveaus erzielt.

Bei quantitativen Handel und Portfoliomanagement erfordert die Anwendung dieser Prinzipien eine statistische Analyse historischer Daten und die Verwendung mathematischer Modelle zur Schätzung der erwarteten Renditen, Standardabweichungen und Covarianzen für verschiedene Vermögenswerte. Anschließend werden Optimierungstechniken verwendet, um die beste Vermögensgewichtszuordnung zu finden. Dieser Prozess beinhaltet oft komplexe mathematische Operationen und umfangreiche Computerverarbeitung - deshalb ist quantitative Analyse in der modernen Finanzwelt so wichtig geworden. Als nächstes werden wir mit spezifischen Python-Beispielen veranschaulichen, wie man optimiert.

Python-Code-Beispiel für das Finden der optimalen Kombination mit Simulationsmethode

Die Berechnung des optimalen Markowitz-Portfolios ist ein mehrstufiger Prozess, der mehrere Schritte beinhaltet, z. B. Datenvorbereitung, Portfoliosimulation und Indikatorberechnung.https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Erhebung von Marktdaten:

Durch dieget_dataDiese Daten sind für die Berechnung von Renditen und Risiken notwendig, die für den Aufbau von Anlageportfolios und die Berechnung von Sharpe-Kennziffern verwendet werden.

2. Berechnung der Rendite und des Risikos:

Diecalculate_returns_riskDiese Funktion wurde verwendet, um die annualisierten Renditen und das annualisierte Risiko (Standard-Abweichung) für jede digitale Währung zu berechnen.

3. Berechnen Sie das optimale Portfolio von Markowitz:

Diecalculate_optimal_portfolioIn jeder Simulation wurden nach dem Zufallsprinzip Vermögenswertgewichte generiert und dann auf der Grundlage dieser Gewichte die erwartete Rendite und das erwartete Risiko des Portfolios berechnet. Durch die zufällige Generierung von Kombinationen mit unterschiedlichen Gewichten ist es möglich, mehrere potenzielle Anlageportfolios zu erforschen, um das optimale zu finden.

Der Zweck des gesamten Prozesses besteht darin, das Anlageportfolio zu finden, das bei einem gegebenen Risikoniveau die am besten erwarteten Renditen liefert. Durch die Simulation mehrerer möglicher Kombinationen können Anleger die Leistung verschiedener Konfigurationen besser verstehen und die Kombination auswählen, die ihren Anlagezielen und ihrer Risikotoleranz am besten entspricht. Diese Methode hilft, Anlageentscheidungen zu optimieren und Investitionen effektiver zu machen.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

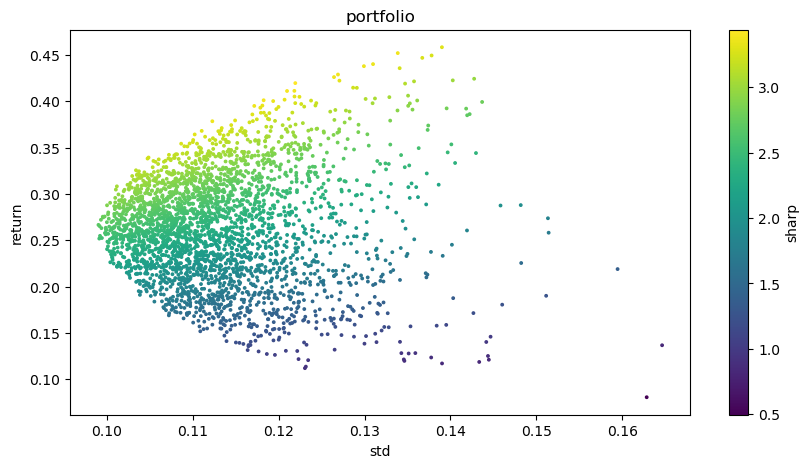
Endgültiges Ergebnis: Die optimale Kombination: Gewicht der BTCUSDT: 0,0721 Gewichtung von ETHUSDT: 0,2704 Gewicht des BNBUSDT: 0,3646 Gewicht der LINKUSDT: 0,1892 Gewicht des BCHUSDT: 0,0829 Gewicht der LTCUSDT: 0,0209 Erwartete Rendite: 0,4195 Erwartetes Risiko (Standard­Abweichung): 0,1219 Sharpe-Verhältnis: 3,4403