Die Ressourcen sind geladen. Beförderung...

Modell für digitale Währungsfaktoren

Schriftsteller:FMZ~Lydia, Erstellt: 2022-10-24 17:37:50, Aktualisiert: 2023-09-15 20:59:38

Faktormodellrahmen

Die Forschungsberichte zum Multifaktormodell der Börse sind umfangreich, mit reichen Theorien und Praktiken. Unabhängig von der Anzahl der Währungen, dem Gesamtmarktwert, dem Handelsvolumen, dem Derivatemarkt usw. im digitalen Währungsmarkt reicht es aus, Faktorenforschung durchzuführen. Dieses Papier richtet sich hauptsächlich an Anfänger quantitativer Strategien und beinhaltet keine komplexen mathematischen Prinzipien und statistische Analyse. Es wird den Binance perpetual future market als Datenquelle verwenden, um einen einfachen Rahmen für die Faktorenforschung aufzubauen, der für die Bewertung von Faktorenindikatoren geeignet ist.

Der Faktor kann als Indikator betrachtet und als Ausdruck geschrieben werden. Der Faktor ändert sich ständig und spiegelt die zukünftigen Einkommensinformationen wider. Im Allgemeinen stellt der Faktor eine Anlagelogik dar.

Zum Beispiel ist die Annahme hinter dem Schlusskursfaktor, dass der Aktienkurs zukünftige Gewinne vorhersagen kann, und je höher der Aktienkurs ist, desto höher (oder möglicherweise niedriger) werden die zukünftigen Gewinne sein. Tatsächlich ist der Aufbau eines Portfolios auf der Grundlage dieses Faktors ein Anlagemodell / -strategie für den Kauf von hochpreisigen Aktien in einer regelmäßigen Runde. Im Allgemeinen werden die Faktoren, die kontinuierlich überschüssige Gewinne erzielen können, auch Alpha genannt. Zum Beispiel wurden der Marktwertfaktor und der Momentumfaktor von der Wissenschaft und der Investitionsgemeinschaft als einst wirksame Faktoren überprüft.

Sowohl der Aktienmarkt als auch der digitale Währungsmarkt sind komplexe Systeme. Es gibt keinen Faktor, der zukünftige Gewinne vollständig vorhersagen kann, aber sie haben immer noch eine gewisse Vorhersagbarkeit. Der effektive Alpha (Investmentmodus) wird jedoch mit mehr Kapitalzufuhr allmählich ungültig. Dieser Prozess wird jedoch andere Modelle auf dem Markt hervorbringen und damit ein neues Alpha hervorrufen. Der Marktwertfaktor war früher eine sehr effektive Strategie auf dem A-Aktienmarkt. Kaufen Sie einfach 10 Aktien mit dem niedrigsten Marktwert und passen Sie sie einmal täglich an. Seit 2007 wird der 10-Jahres-Backtest mehr als das 400-fache der Gewinne ergeben, was den Gesamtmarkt weit übersteigt.

Eine bessere Strategie kann durch die Kombination mehrerer unabhängiger wirksamer Faktoren aufgebaut werden.

import requests
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import requests, zipfile, io
%matplotlib inline

Datenquelle

Bislang haben die stündlichen K-Liniendaten der Binance USDT-Perpetual Futures von Anfang 2022 bis heute 150 Währungen überschritten. Wie bereits erwähnt, ist das Faktormodell ein Währungsauswahlmodell, das sich an alle Währungen und nicht an eine bestimmte Währung orientiert. Die K-Liniendaten umfassen Öffnungs- und Schließungshöchstpreise, Handelsvolumen, Anzahl der Transaktionen, Taker Buy-Volumen und andere Daten. Diese Daten sind sicherlich nicht die Quelle aller Faktoren, wie der US-Aktienindex, Zinsanstiegserwartung, Rentabilität, Daten über die Kette, Popularität in den sozialen Medien und so weiter. Ungewöhnliche Datenquellen können auch effektive Alpha finden, aber das Basispreisvolumen ist auch ausreichend.

## Current trading pair
Info = requests.get('https://fapi.binance.com/fapi/v1/exchangeInfo')
symbols = [s['symbol'] for s in Info.json()['symbols']]
symbols = list(filter(lambda x: x[-4:] == 'USDT', [s.split('_')[0] for s in symbols]))
print(symbols)

Ausgeschaltet:

['BTCUSDT', 'ETHUSDT', 'BCHUSDT', 'XRPUSDT', 'EOSUSDT', 'LTCUSDT', 'TRXUSDT', 'ETCUSDT', 'LINKUSDT',
'XLMUSDT', 'ADAUSDT', 'XMRUSDT', 'DASHUSDT', 'ZECUSDT', 'XTZUSDT', 'BNBUSDT', 'ATOMUSDT', 'ONTUSDT',
'IOTAUSDT', 'BATUSDT', 'VETUSDT', 'NEOUSDT', 'QTUMUSDT', 'IOSTUSDT', 'THETAUSDT', 'ALGOUSDT', 'ZILUSDT',
'KNCUSDT', 'ZRXUSDT', 'COMPUSDT', 'OMGUSDT', 'DOGEUSDT', 'SXPUSDT', 'KAVAUSDT', 'BANDUSDT', 'RLCUSDT',
'WAVESUSDT', 'MKRUSDT', 'SNXUSDT', 'DOTUSDT', 'DEFIUSDT', 'YFIUSDT', 'BALUSDT', 'CRVUSDT', 'TRBUSDT',
'RUNEUSDT', 'SUSHIUSDT', 'SRMUSDT', 'EGLDUSDT', 'SOLUSDT', 'ICXUSDT', 'STORJUSDT', 'BLZUSDT', 'UNIUSDT',
'AVAXUSDT', 'FTMUSDT', 'HNTUSDT', 'ENJUSDT', 'FLMUSDT', 'TOMOUSDT', 'RENUSDT', 'KSMUSDT', 'NEARUSDT',
'AAVEUSDT', 'FILUSDT', 'RSRUSDT', 'LRCUSDT', 'MATICUSDT', 'OCEANUSDT', 'CVCUSDT', 'BELUSDT', 'CTKUSDT',
'AXSUSDT', 'ALPHAUSDT', 'ZENUSDT', 'SKLUSDT', 'GRTUSDT', '1INCHUSDT', 'CHZUSDT', 'SANDUSDT', 'ANKRUSDT',
'BTSUSDT', 'LITUSDT', 'UNFIUSDT', 'REEFUSDT', 'RVNUSDT', 'SFPUSDT', 'XEMUSDT', 'BTCSTUSDT', 'COTIUSDT',
'CHRUSDT', 'MANAUSDT', 'ALICEUSDT', 'HBARUSDT', 'ONEUSDT', 'LINAUSDT', 'STMXUSDT', 'DENTUSDT', 'CELRUSDT',
'HOTUSDT', 'MTLUSDT', 'OGNUSDT', 'NKNUSDT', 'SCUSDT', 'DGBUSDT', '1000SHIBUSDT', 'ICPUSDT', 'BAKEUSDT',
'GTCUSDT', 'BTCDOMUSDT', 'TLMUSDT', 'IOTXUSDT', 'AUDIOUSDT', 'RAYUSDT', 'C98USDT', 'MASKUSDT', 'ATAUSDT',
'DYDXUSDT', '1000XECUSDT', 'GALAUSDT', 'CELOUSDT', 'ARUSDT', 'KLAYUSDT', 'ARPAUSDT', 'CTSIUSDT', 'LPTUSDT',
'ENSUSDT', 'PEOPLEUSDT', 'ANTUSDT', 'ROSEUSDT', 'DUSKUSDT', 'FLOWUSDT', 'IMXUSDT', 'API3USDT', 'GMTUSDT',
'APEUSDT', 'BNXUSDT', 'WOOUSDT', 'FTTUSDT', 'JASMYUSDT', 'DARUSDT', 'GALUSDT', 'OPUSDT', 'BTCUSDT',
'ETHUSDT', 'INJUSDT', 'STGUSDT', 'FOOTBALLUSDT', 'SPELLUSDT', '1000LUNCUSDT', 'LUNA2USDT', 'LDOUSDT',
'CVXUSDT']

print(len(symbols))

Ausgeschaltet:

#Function to obtain any period of K-line
def GetKlines(symbol='BTCUSDT',start='2020-8-10',end='2021-8-10',period='1h',base='fapi',v = 'v1'):
    Klines = []
    start_time = int(time.mktime(datetime.strptime(start, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000
    end_time =  min(int(time.mktime(datetime.strptime(end, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000,time.time()*1000)
    intervel_map = {'m':60*1000,'h':60*60*1000,'d':24*60*60*1000}
    while start_time < end_time:
        mid_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        url = 'https://'+base+'.binance.com/'+base+'/'+v+'/klines?symbol=%s&interval=%s&startTime=%s&endTime=%s&limit=1000'%(symbol,period,start_time,mid_time)
        res = requests.get(url)
        res_list = res.json()
        if type(res_list) == list and len(res_list) > 0:
            start_time = res_list[-1][0]+int(period[:-1])*intervel_map[period[-1]]
            Klines += res_list
        if type(res_list) == list and len(res_list) == 0:
            start_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        if mid_time >= end_time:
            break
    df = pd.DataFrame(Klines,columns=['time','open','high','low','close','amount','end_time','volume','count','buy_amount','buy_volume','null']).astype('float')
    df.index = pd.to_datetime(df.time,unit='ms')
    return df

start_date = '2022-1-1'
end_date = '2022-09-14'
period = '1h'
df_dict = {}
for symbol in symbols:
    df_s = GetKlines(symbol=symbol,start=start_date,end=end_date,period=period,base='fapi',v='v1')
    if not df_s.empty:
        df_dict[symbol] = df_s

symbols = list(df_dict.keys())
print(df_s.columns)

Ausgeschaltet:

Index(['time', 'open', 'high', 'low', 'close', 'amount', 'end_time', 'volume',
       'count', 'buy_amount', 'buy_volume', 'null'],
      dtype='object')

Die Daten, an denen wir interessiert sind: Schlusskurs, Eröffnungskurs, Handelsvolumen, Anzahl der Transaktionen und Taker Buy-Anteil werden zuerst aus den K-Liniendaten extrahiert.

df_close = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_open = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_volume = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_buy_ratio = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_count = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
for symbol in df_dict.keys():
    df_s = df_dict[symbol]
    df_close[symbol] = df_s.close
    df_open[symbol] = df_s.open
    df_volume[symbol] = df_s.volume
    df_count[symbol] = df_s['count']
    df_buy_ratio[symbol] = df_s.buy_amount/df_s.amount
df_close = df_close.dropna(how='all')
df_open = df_open.dropna(how='all')
df_volume = df_volume.dropna(how='all')
df_count = df_count.dropna(how='all')
df_buy_ratio = df_buy_ratio.dropna(how='all')

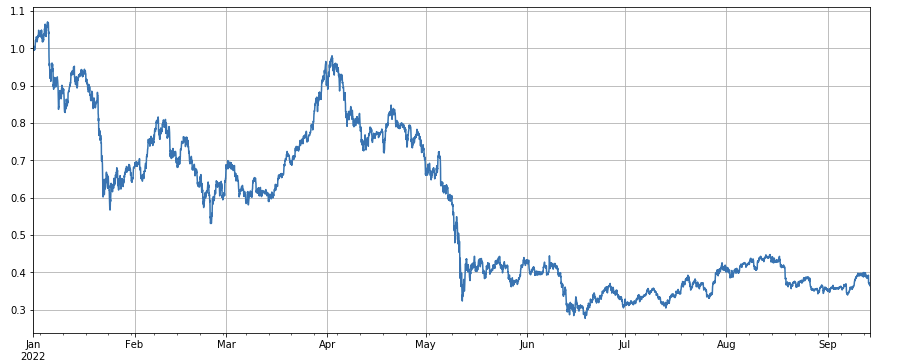
Die Gesamtentwicklung des Marktindex ist düster, der von Anfang des Jahres bis zu den letzten Tagen um 60% zurückgegangen ist.

df_norm = df_close/df_close.fillna(method='bfill').iloc[0] #normalization
df_norm.mean(axis=1).plot(figsize=(15,6),grid=True);
#Final index profit chart

Urteil über die Gültigkeit von Faktoren

Regressionsmethode Die Rendite der folgenden Periode ist die abhängige Variable, und der zu prüfende Faktor ist die unabhängige Variable. Der durch Regression gewonnene Koeffizient ist auch die Rendite des Faktors. Nachdem die Regressionsgleichung konstruiert wurde, werden die Gültigkeit und Volatilität von Faktoren im Allgemeinen anhand des absoluten Mittelwerts des Koeffizienten t-Wertes, des Anteils der absoluten Wertfolge des Koeffizienten t-Wertes größer als 2, der jährlichen Faktorrendite, der jährlichen Faktorgewinnvolatilität und des Sharpe-Verhältnisses des Faktorgewinns betrachtet. Mehrere Faktoren können gleichzeitig regresiert werden. Bitte beachten Sie das Barra-Dokument für Details.
IC, IR und andere Indikatoren Der sogenannte IC ist der Korrelationskoeffizient zwischen dem Faktor und der Rendite der nächsten Periode. Jetzt wird RANK_ IC auch allgemein verwendet, es ist der Korrelationskoeffizient zwischen der Faktorrangliste und der nächsten Rendite der Aktie. IR ist im Allgemeinen der mittlere Wert der IC-Sequenz / die Standardabweichung der IC-Sequenz.
Stratifizierte Regressionsmethode In diesem Artikel werden wir diese Methode verwenden, die darin besteht, die Währungen nach den zu prüfenden Faktoren zu sortieren, sie in N-Gruppen für das Gruppen-Backtesting zu teilen und einen festen Zeitraum für die Positionsanpassung zu verwenden. Wenn die Situation ideal ist, zeigt die Rendite der Währungen der Gruppe N eine gute Monotonie, wächst oder sinkt monoton, und die Einkommenslücke jeder Gruppe ist groß. Solche Faktoren spiegeln sich in einer guten Diskriminierung wider. Wenn die erste Gruppe die höchsten Gewinne und die letzte Gruppe die niedrigsten Gewinne hat, dann gehen Sie in der ersten Gruppe lang und in der letzten Gruppe kurz, um die endgültige Rendite zu erhalten, die der Referenzindikator des Sharp-Verhältnisses ist.

Tatsächliche Rückprüfung

Die zu wählenden Münzen werden in 3 Gruppen unterteilt, basierend auf der Rangfolge der Faktoren von kleinster bis größter. Jede Gruppe von Währungen macht etwa 1/3 der Gesamtzahl aus. Wenn ein Faktor effektiv ist, desto geringer die Anzahl der Punkte in jeder Gruppe, desto höher wird die Rendite sein, aber es bedeutet auch, dass jede Währung relativ mehr Mittel zugewiesen hat. Wenn die Long- und Short-Positionen doppelter Hebelwirkung sind, und die erste Gruppe und die letzte Gruppe 10 Währungen sind, dann macht eine Währung 10% der Gesamtzahl aus. Wenn eine Währung, die kurz gehalten wird, verdoppelt wird, dann werden 20% abgezogen; Wenn die Anzahl der Gruppen 50 ist, dann werden 4% abgezogen. Diversifizierende Währungen können das Risiko von schwarzen Schwanen reduzieren.

Im Allgemeinen kann die Fähigkeit der Faktorvorhersage grob nach der Rendite und dem Sharpe-Verhältnis des endgültigen Backtests bewertet werden. Darüber hinaus muss auch darauf verwiesen werden, ob der Faktor-Ausdruck einfach ist, empfindlich für die Größe der Gruppierung, empfindlich für das Positionsanpassungsintervall und empfindlich für die anfängliche Zeit des Backtests.

In Bezug auf die Häufigkeit der Positionsanpassung hat der Aktienmarkt in der Regel eine Periode von 5 Tagen, 10 Tagen und einem Monat. Für den digitalen Währungsmarkt ist eine solche Periode jedoch zweifellos zu lang und der Markt im realen Bot wird in Echtzeit überwacht. Es ist nicht notwendig, sich an einen bestimmten Zeitraum zu halten, um die Positionen erneut anzupassen. Daher passen wir im realen Bot die Positionen in Echtzeit oder in kurzer Zeit an.

Wie man die Position schließt, kann die Position nach der traditionellen Methode geschlossen werden, wenn sie beim nächsten Sortieren nicht in der Gruppe ist. Im Falle der Echtzeit-Positionsanpassung können sich jedoch einige Währungen gerade an der Grenze befinden, was zum Hin und Her-Positionsschließen führen kann. Daher nimmt diese Strategie die Methode an, auf Gruppenänderungen zu warten und dann die Position zu schließen, wenn die Position in der entgegengesetzten Richtung geöffnet werden muss. Zum Beispiel geht die erste Gruppe lang. Wenn die Währungen im Status der langen Position in die dritte Gruppe aufgeteilt sind, schließen Sie dann die Position und gehen kurz. Wenn die Position in einem festen Zeitraum geschlossen wird, z. B. jeden Tag oder alle 8 Stunden, können Sie die Position auch schließen, ohne in einer Gruppe zu sein. Versuchen Sie es so viel wie möglich.

#Backtest engine
class Exchange:
    
    def __init__(self, trade_symbols, fee=0.0004, initial_balance=10000):
        self.initial_balance = initial_balance #Initial assets
        self.fee = fee
        self.trade_symbols = trade_symbols
        self.account = {'USDT':{'realised_profit':0, 'unrealised_profit':0, 'total':initial_balance, 'fee':0, 'leverage':0, 'hold':0}}
        for symbol in trade_symbols:
            self.account[symbol] = {'amount':0, 'hold_price':0, 'value':0, 'price':0, 'realised_profit':0,'unrealised_profit':0,'fee':0}
            
    def Trade(self, symbol, direction, price, amount):
        
        cover_amount = 0 if direction*self.account[symbol]['amount'] >=0 else min(abs(self.account[symbol]['amount']), amount)
        open_amount = amount - cover_amount
        self.account['USDT']['realised_profit'] -= price*amount*self.fee #Net of fees
        self.account['USDT']['fee'] += price*amount*self.fee
        self.account[symbol]['fee'] += price*amount*self.fee

        if cover_amount > 0: #Close position first
            self.account['USDT']['realised_profit'] += -direction*(price - self.account[symbol]['hold_price'])*cover_amount  #Profits
            self.account[symbol]['realised_profit'] += -direction*(price - self.account[symbol]['hold_price'])*cover_amount
            
            self.account[symbol]['amount'] -= -direction*cover_amount
            self.account[symbol]['hold_price'] = 0 if self.account[symbol]['amount'] == 0 else self.account[symbol]['hold_price']
            
        if open_amount > 0:
            total_cost = self.account[symbol]['hold_price']*direction*self.account[symbol]['amount'] + price*open_amount
            total_amount = direction*self.account[symbol]['amount']+open_amount
            
            self.account[symbol]['hold_price'] = total_cost/total_amount
            self.account[symbol]['amount'] += direction*open_amount
                    
    
    def Buy(self, symbol, price, amount):
        self.Trade(symbol, 1, price, amount)
        
    def Sell(self, symbol, price, amount):
        self.Trade(symbol, -1, price, amount)
        
    def Update(self, close_price): #Update assets
        self.account['USDT']['unrealised_profit'] = 0
        self.account['USDT']['hold'] = 0
        for symbol in self.trade_symbols:
            if not np.isnan(close_price[symbol]):
                self.account[symbol]['unrealised_profit'] = (close_price[symbol] - self.account[symbol]['hold_price'])*self.account[symbol]['amount']
                self.account[symbol]['price'] = close_price[symbol]
                self.account[symbol]['value'] = abs(self.account[symbol]['amount'])*close_price[symbol]
                self.account['USDT']['hold'] += self.account[symbol]['value']
                self.account['USDT']['unrealised_profit'] += self.account[symbol]['unrealised_profit']
        self.account['USDT']['total'] = round(self.account['USDT']['realised_profit'] + self.initial_balance + self.account['USDT']['unrealised_profit'],6)
        self.account['USDT']['leverage'] = round(self.account['USDT']['hold']/self.account['USDT']['total'],3)

#Function of test factor
def Test(factor, symbols, period=1, N=40, value=300):
    e = Exchange(symbols, fee=0.0002, initial_balance=10000)
    res_list = []
    index_list = []
    factor = factor.dropna(how='all')
    for idx, row in factor.iterrows():
        if idx.hour % period == 0:
            buy_symbols =  row.sort_values().dropna()[0:N].index
            sell_symbols = row.sort_values().dropna()[-N:].index
            prices = df_close.loc[idx,]
            index_list.append(idx)
            for symbol in symbols:
                if symbol in buy_symbols and e.account[symbol]['amount'] <= 0:
                    e.Buy(symbol,prices[symbol],value/prices[symbol]-e.account[symbol]['amount'])
                if symbol in sell_symbols and e.account[symbol]['amount'] >= 0:
                    e.Sell(symbol,prices[symbol], value/prices[symbol]+e.account[symbol]['amount'])
            e.Update(prices)
            res_list.append([e.account['USDT']['total'],e.account['USDT']['hold']])
    return pd.DataFrame(data=res_list, columns=['total','hold'],index = index_list)

Einfacher Faktortest

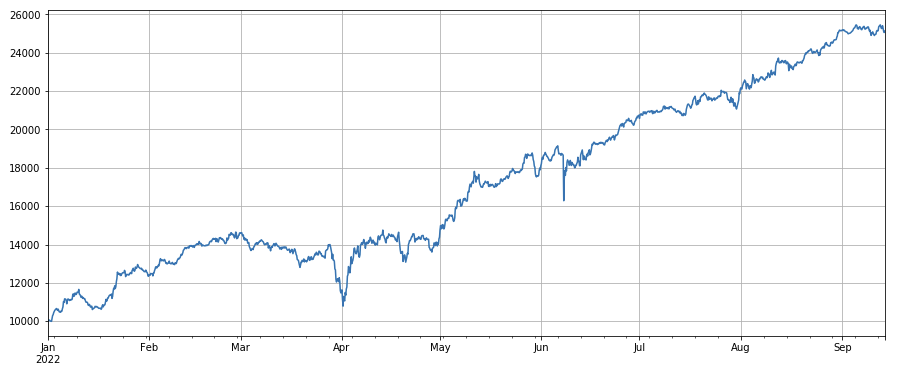
Handelsvolumenfaktor: Einfache Long-Währungen mit geringem Handelsvolumen und kurze Währungen mit hohem Handelsvolumen, die sehr gut abschneiden, was darauf hindeutet, dass beliebte Währungen tendenziell sinken.

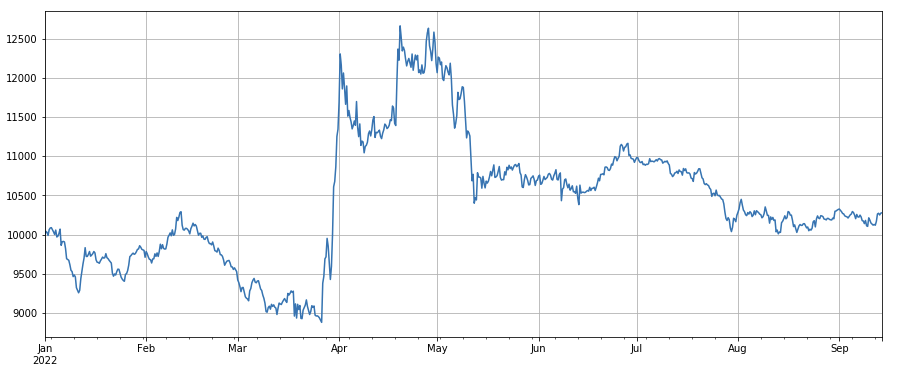
Handelspreisfaktor: Die Wirkung von Long-Währungen mit niedrigen Preisen und von Short-Währungen mit hohen Preisen sind beide normal.

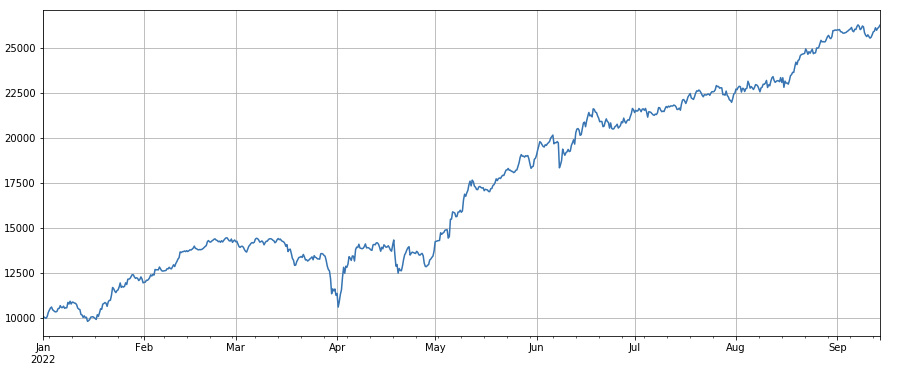
Transaktionszahlfaktor: Die Leistung ist dem Transaktionsvolumen sehr ähnlich. Es ist offensichtlich, dass die Korrelation zwischen dem Transaktionsvolumenfaktor und dem Transaktionszahlfaktor sehr hoch ist. Tatsächlich hat die durchschnittliche Korrelation zwischen ihnen in verschiedenen Währungen 0,97 erreicht, was darauf hinweist, dass die beiden Faktoren sehr ähnlich sind. Dieser Faktor muss bei der Synthese mehrerer Faktoren berücksichtigt werden.

3h-Impulsfaktor: (df_close - df_close. shift (3)) /df_ close. shift(3). Das heißt, der 3-stündige Anstieg des Faktors. Die Rücktest-Ergebnisse zeigen, dass der 3-stündige Anstieg offensichtliche Regressionsmerkmale aufweist, dh der Anstieg später leichter fällt. Die Gesamtleistung ist in Ordnung, aber es gibt auch eine lange Periode des Rückzugs und der Oszillation.

24-Stunden-Impulsfaktor: Das Ergebnis der 24-Stunden-Positionsanpassung ist gut, der Ertrag ähnelt dem 3-Stunden-Impulsfaktor und der Abzug ist kleiner.

Der Veränderungsfaktor des Transaktionsvolumens: df_ volume.rolling ((24).mean ((() /df_ volume. rolling (96). mean ((), das heißt das Verhältnis des Transaktionsvolumens am letzten Tag zum Transaktionsvolumen in den letzten drei Tagen. Die Position wird alle 8 Stunden angepasst. Die Ergebnisse des Backtestings waren gut, und der Rückzug war auch relativ niedrig, was darauf hindeutet, dass diejenigen mit aktivem Transaktionsvolumen eher zu sinken neigten.

Der Wechselfaktor der Transaktionszahl: df_ count.rolling(24).mean() /df_ count.rolling(96). mean (), das heißt das Verhältnis der Transaktionszahl am letzten Tag zur Transaktionszahl in den letzten drei Tagen. Die Position wird alle 8 Stunden angepasst. Die Ergebnisse des Backtestings waren gut, und der Rückzug ist auch relativ gering, was darauf hindeutet, dass diejenigen mit aktivem Transaktionsvolumen eher zu sinken neigten.

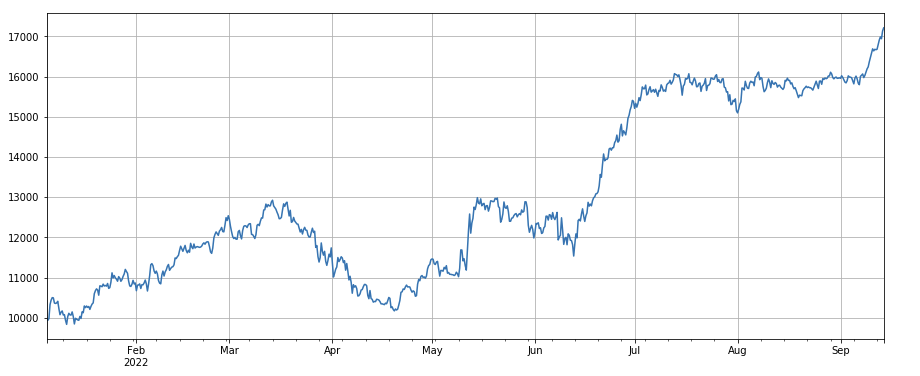
Veränderungsfaktor des Wertes einer einzelnen Transaktion: - ((df_volume.rolling(24).mean()/df_count.rolling(24.mean())/(df_volume.rolling(24.mean()/df_count.rolling(96.mean()) , d. h. das Verhältnis des Transaktionswerts des letzten Tages zum Transaktionswert der letzten drei Tage, und die Position wird alle 8 Stunden angepasst. Dieser Faktor ist auch stark mit dem Transaktionsvolumenfaktor korreliert.

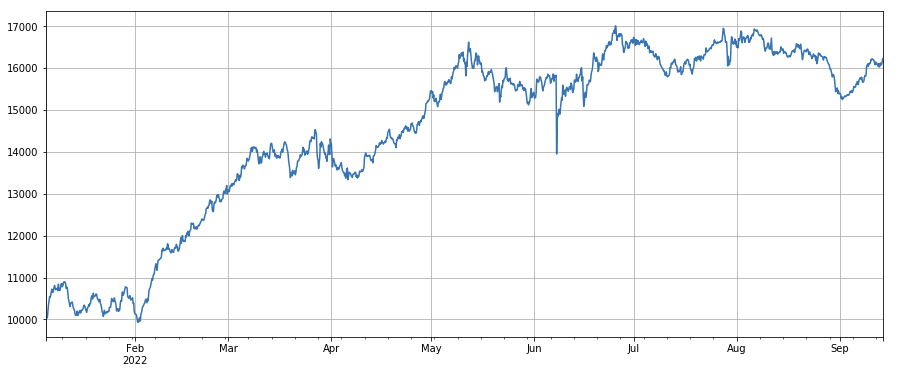
Veränderungsfaktor des Takers nach Transaktionsanteil: df_buy_ratio.rolling ((24).mean() /df_buy_ratio.rolling ((96).mean(), das heißt, das Verhältnis des Takers nach Volumen zum Gesamttransaktionsvolumen am letzten Tag zum Transaktionswert in den letzten drei Tagen, und die Position wird alle 8 Stunden angepasst. Dieser Faktor funktioniert ziemlich gut und hat wenig Korrelation mit dem Transaktionsvolumenfaktor.

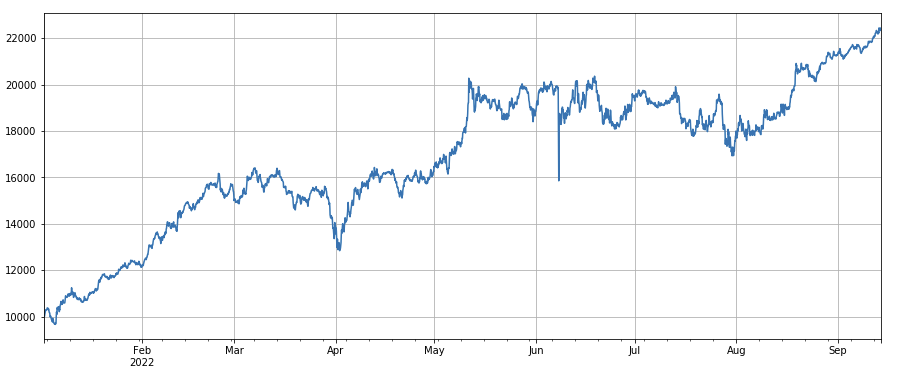
Volatilitätsfaktor: (df_close/df_open).rolling(24).std(), gehen lange Währungen mit geringer Volatilität, es hat einen bestimmten Effekt.

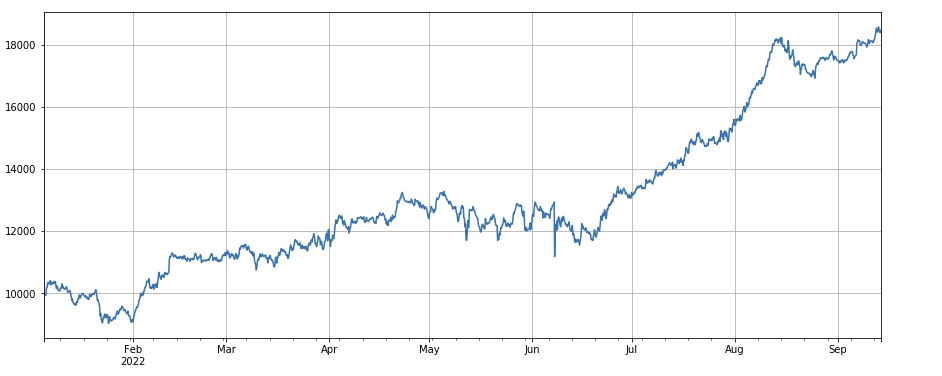
Korrelationsfaktor zwischen Transaktionsvolumen und Schlusskurs: df_close.rolling(96).corr(df_volume), der Schlusskurs in den letzten vier Tagen hat einen Korrelationsfaktor des Transaktionsvolumens, der insgesamt gut abgeschnitten hat.

Die hier aufgeführten Faktoren basieren auf dem Preisvolumen. Tatsächlich kann die Kombination von Faktorformeln ohne offensichtliche Logik sehr komplex sein.https://github.com/STHSF/alpha101.

#transaction volume
factor_volume = df_volume
factor_volume_res = Test(factor_volume, symbols, period=4)
factor_volume_res.total.plot(figsize=(15,6),grid=True);

#transaction price
factor_close = df_close
factor_close_res = Test(factor_close, symbols, period=8)
factor_close_res.total.plot(figsize=(15,6),grid=True);

#transaction count
factor_count = df_count
factor_count_res = Test(factor_count, symbols, period=8)
factor_count_res.total.plot(figsize=(15,6),grid=True);

print(df_count.corrwith(df_volume).mean())

0.9671246744996017

#3h momentum factor
factor_1 =  (df_close - df_close.shift(3))/df_close.shift(3)
factor_1_res = Test(factor_1,symbols,period=1)
factor_1_res.total.plot(figsize=(15,6),grid=True);

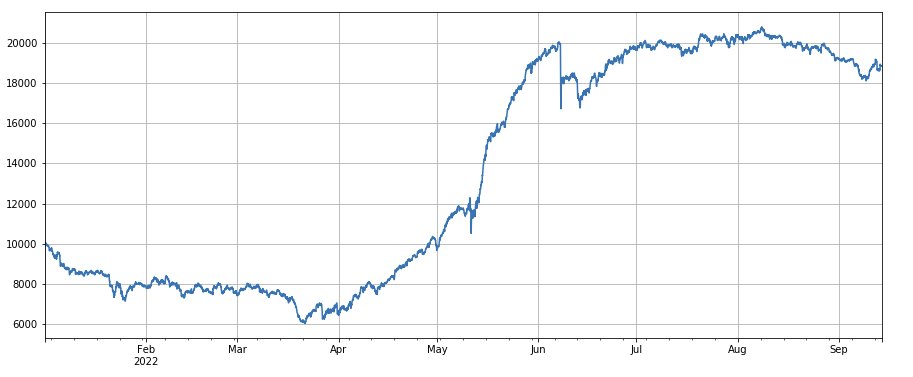
#24h momentum factor
factor_2 =  (df_close - df_close.shift(24))/df_close.shift(24)
factor_2_res = Test(factor_2,symbols,period=24)
tamenxuanfactor_2_res.total.plot(figsize=(15,6),grid=True);

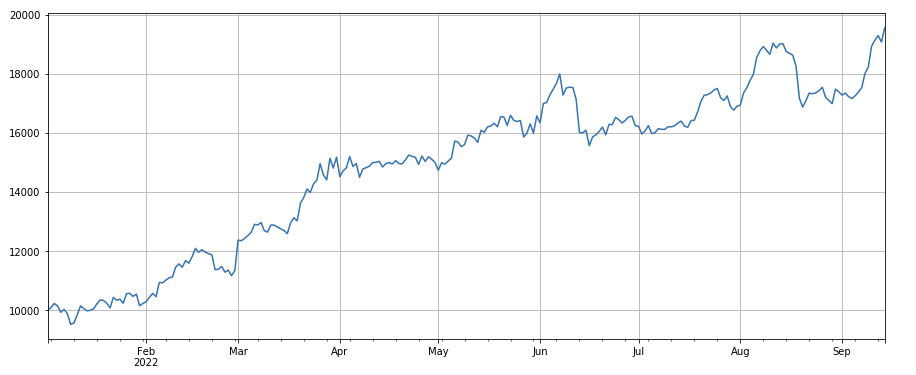
#factor of transaction volume
factor_3 = df_volume.rolling(24).mean()/df_volume.rolling(96).mean()
factor_3_res = Test(factor_3, symbols, period=8)
factor_3_res.total.plot(figsize=(15,6),grid=True);

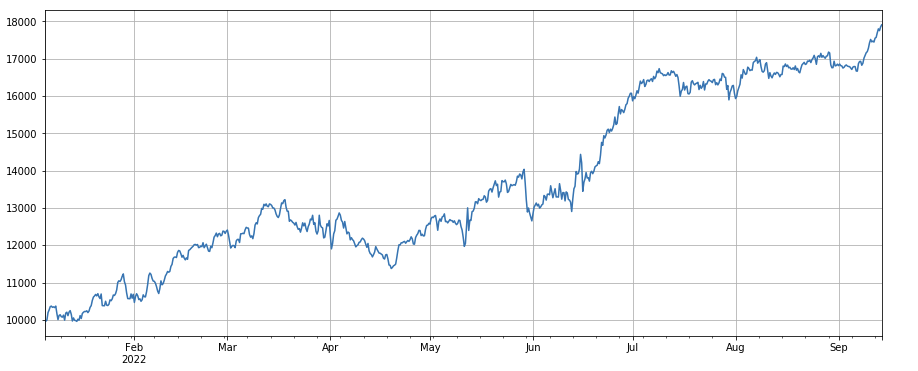
#factor of transaction number
factor_4 = df_count.rolling(24).mean()/df_count.rolling(96).mean()
factor_4_res = Test(factor_4, symbols, period=8)
factor_4_res.total.plot(figsize=(15,6),grid=True);

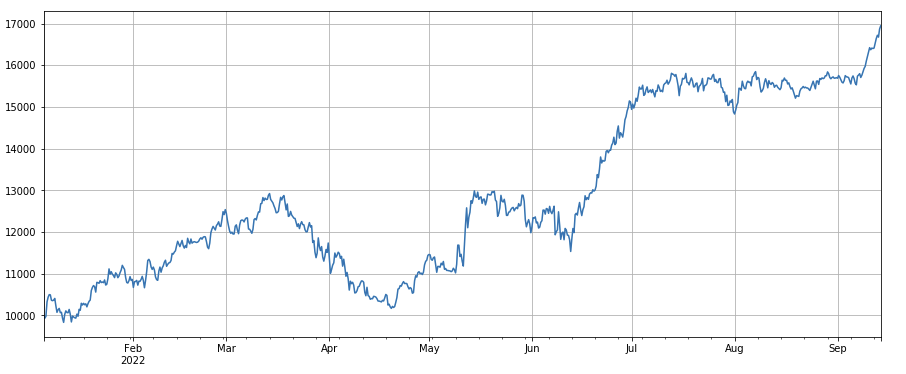
#factor correlation
print(factor_4.corrwith(factor_3).mean())

0.9707239580854841

#single transaction value factor
factor_5 = -(df_volume.rolling(24).mean()/df_count.rolling(24).mean())/(df_volume.rolling(24).mean()/df_count.rolling(96).mean())
factor_5_res = Test(factor_5, symbols, period=8)
factor_5_res.total.plot(figsize=(15,6),grid=True);

print(factor_4.corrwith(factor_5).mean())

0.861206620552479

#proportion factor of taker by transaction
factor_6 = df_buy_ratio.rolling(24).mean()/df_buy_ratio.rolling(96).mean()
factor_6_res = Test(factor_6, symbols, period=4)
factor_6_res.total.plot(figsize=(15,6),grid=True);

print(factor_3.corrwith(factor_6).mean())

0.1534572192503726

#volatility factor
factor_7 = (df_close/df_open).rolling(24).std()
factor_7_res = Test(factor_7, symbols, period=2)
factor_7_res.total.plot(figsize=(15,6),grid=True);

#correlation factor between transaction volume and closing price
factor_8 = df_close.rolling(96).corr(df_volume)
factor_8_res = Test(factor_8, symbols, period=4)
factor_8_res.total.plot(figsize=(15,6),grid=True);

Multifaktor-Synthese

Es ist sicherlich der wichtigste Teil des Strategiebauprozesses, ständig neue wirksame Faktoren zu entdecken, aber ohne eine gute Faktor-Synthese-Methode kann ein hervorragender einzelner Alpha-Faktor nicht seine maximale Rolle spielen.

Gleichgewichtsmethode: Alle zu synthetisierenden Faktoren werden mit gleichem Gewicht addiert, um nach der Synthese neue Faktoren zu erhalten.

Gewichtungsmethode der historischen Faktorrendite: Alle zu kombinierenden Faktoren werden nach dem arithmetischen Mittel der historischen Faktorrendite in der letzten Periode als Gewicht addiert, um nach der Synthese einen neuen Faktor zu erhalten.

Maximieren IC_IR-Gewichtungsmethode: Der durchschnittliche IC-Wert des Composite-Faktors über einen Zeitraum der Geschichte wird als Schätzung des IC-Wertes des Composite-Faktors im nächsten Zeitraum verwendet, und die Kovarianzmatrix des historischen IC-Wertes wird als Schätzung der Volatilität des Composite-Faktors im nächsten Zeitraum verwendet. Gemäß IC_IR ist der erwartete Wert von IC geteilt durch die Standardabweichung von IC, um die optimale Gewichtslösung des maximalen Composite-Faktors IC_IR zu erhalten.

Hauptkomponentenanalyse (PCA): PCA ist eine gängige Methode zur Dimensionalisierungsreduktion von Daten, und die Korrelation zwischen den Faktoren kann hoch sein.

In diesem Papier wird manuell auf die Zuweisung der Faktorvalidität verwiesen.ae933a8c-5a94-4d92-8f33-d92b70c36119.pdf

Bei der Prüfung einzelner Faktoren ist die Sortierung festgelegt, aber die Multifaktor-Synthese muss völlig verschiedene Daten kombinieren, so dass alle Faktoren standardisiert werden müssen und der extreme Wert und der fehlende Wert generell entfernt werden müssen. Hier verwenden wir df_ Volumen\Faktor_ 1\Faktor_ 7\Faktor_ 6\Faktor_ 8 für die Synthese.

#standardize functions, remove missing values and extreme values, and standardize
def norm_factor(factor):
    factor = factor.dropna(how='all')
    factor_clip = factor.apply(lambda x:x.clip(x.quantile(0.2), x.quantile(0.8)),axis=1)
    factor_norm = factor_clip.add(-factor_clip.mean(axis=1),axis ='index').div(factor_clip.std(axis=1),axis ='index')
    return factor_norm


df_volume_norm = norm_factor(df_volume)
factor_1_norm = norm_factor(factor_1)
factor_6_norm = norm_factor(factor_6)
factor_7_norm = norm_factor(factor_7)
factor_8_norm = norm_factor(factor_8)

factor_total = 0.6*df_volume_norm + 0.4*factor_1_norm + 0.2*factor_6_norm + 0.3*factor_7_norm + 0.4*factor_8_norm
factor_total_res = Test(factor_total, symbols, period=8)
factor_total_res.total.plot(figsize=(15,6),grid=True);

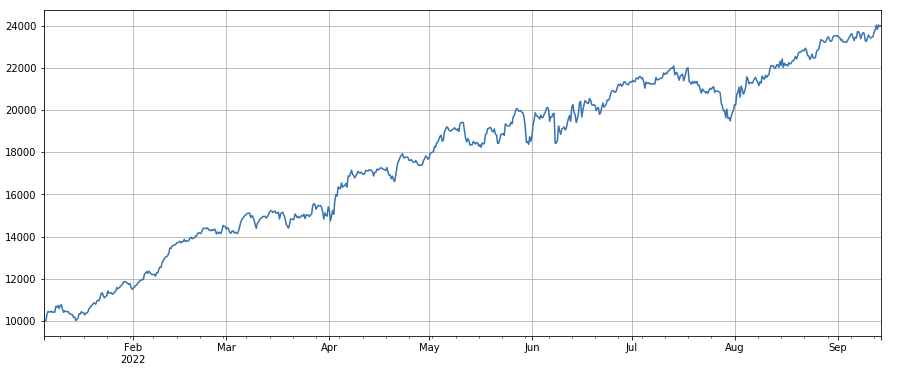
Zusammenfassung

In diesem Artikel wird die Testmethode des Single-Faktors eingeführt und gemeinsame Einzelfaktoren getestet und zunächst die Methode der Multi-Faktor-Synthese eingeführt. Es gibt jedoch viele Forschungsinhalte von Multi-Faktor. Jeder Punkt, der in dem Papier erwähnt wird, kann weiterentwickelt werden. Es ist eine praktikable Möglichkeit, die Forschung zu verschiedenen Strategien in die Erforschung von Alpha-Faktor zu verwandeln. Die Verwendung der Faktormethodik kann die Verifizierung von Handelsideen erheblich beschleunigen und es gibt viele Referenzmaterialien.

Der echte Bot von:https://www.fmz.com/robot/486605

Verwandt

Mehr