Paarhandel auf Basis datengetriebener Technologie
Schriftsteller:FMZ~Lydia, Erstellt: 2023-01-05 09:10:25, aktualisiert: 2024-12-19 00:27:10
Paarhandel auf Basis datengetriebener Technologie
Pair Trading ist ein gutes Beispiel für die Formulierung von Handelsstrategien auf der Grundlage mathematischer Analyse.
Grundprinzipien
Nehmen wir an, Sie haben ein Paar von Anlagezielen X und Y, die einige potenzielle Verbindungen haben. Zum Beispiel produzieren zwei Unternehmen die gleichen Produkte, wie Pepsi Cola und Coca Cola. Sie möchten, dass das Preisverhältnis oder die Basis-Spreads (auch als Preisdifferenz bezeichnet) der beiden im Laufe der Zeit unverändert bleiben. Aufgrund der vorübergehenden Veränderungen in Angebot und Nachfrage, wie z. B. einer großen Kauf-/Verkaufsanordnung eines Anlageziels und der Reaktion auf die wichtigen Nachrichten eines der Unternehmen, kann die Preisdifferenz zwischen den beiden Paaren von Zeit zu Zeit unterschiedlich sein. In diesem Fall bewegt sich ein Anlageobjekt nach oben, während das andere sich relativ zum anderen bewegt. Wenn Sie möchten, dass diese Meinungsverschiedenheit im Laufe der Zeit wieder normal wird, können Sie Handelsmöglichkeiten (oder Arbitragsmöglichkeiten) finden.
Wenn es eine vorübergehende Preisdifferenz gibt, verkaufen Sie das Investitionsobjekt mit hervorragender Leistung (das steigende Investitionsobjekt) und kaufen das Investitionsobjekt mit schlechter Leistung (das fallende Investitionsobjekt). Sie sind sicher, dass die Zinsspanne zwischen den beiden Investitionsobjekten schließlich durch den Fall des Investitionsobjekts mit hervorragender Leistung oder den Anstieg des Investitionsobjekts mit schlechter Leistung oder beides fallen wird. Ihre Transaktion wird in all diesen ähnlichen Situationen Geld verdienen. Wenn die Investitionsobjekte ohne Änderung der Preisdifferenz zwischen ihnen zusammen nach oben oder unten gehen, werden Sie kein Geld verdienen oder verlieren.
Der Handel mit Paaren ist daher eine marktneutrale Handelsstrategie, die es den Händlern ermöglicht, von fast allen Marktbedingungen zu profitieren: Aufwärtstrend, Abwärtstrend oder horizontale Konsolidierung.
Erläutern Sie das Konzept: zwei hypothetische Investitionsziele
- Aufbau unserer Forschungsumgebung auf der FMZ Quant-Plattform
In diesem Artikel verwenden wir die FMZ Quant Plattform (FMZ.COM), um unsere Forschungsumgebung zu erstellen, hauptsächlich um die bequeme und schnelle API-Schnittstelle und das gut verpackte Docker-System dieser Plattform später zu verwenden.
In der offiziellen Bezeichnung der FMZ Quant-Plattform wird dieses Docker-System das Docker-System genannt.
Bitte beachten Sie meinen vorherigen Artikel über die Bereitstellung eines Dockers und eines Roboters:https://www.fmz.com/bbs-topic/9864.
Leser, die ihren eigenen Cloud-Computing-Server kaufen möchten, um Dockers zu implementieren, können sich auf diesen Artikel beziehen:https://www.fmz.com/digest-topic/5711.
Nachdem wir den Cloud-Computing-Server und das Docker-System erfolgreich bereitgestellt haben, installieren wir als nächstes das derzeit größte Artefakt von Python: Anaconda.
Um alle relevanten Programmumgebungen (Abhängigkeitsbibliotheken, Versionsmanagement usw.) zu realisieren, die in diesem Artikel erforderlich sind, ist es am einfachsten, Anaconda zu verwenden.
Für die Installationsmethode von Anaconda lesen Sie bitte den offiziellen Anleitungsbericht zu Anaconda:https://www.anaconda.com/distribution/.
In diesem Artikel werden auch numpy und pandas verwendet, zwei beliebte und wichtige Bibliotheken im Python-Wissenschaftsrechnen.
Die obige Grundlagenarbeit kann sich auch auf meine früheren Artikel beziehen, die einführen, wie man die Anaconda-Umgebung und die Numpy- und Pandas-Bibliotheken einrichtet.https://www.fmz.com/bbs-topic/9863.
Als nächstes wollen wir Code verwenden, um ein
import numpy as np
import pandas as pd
import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)
import matplotlib.pyplot as plt
Ja, wir werden auch matplotlib verwenden, eine sehr bekannte Diagrammbibliothek in Python.
Lassen Sie uns ein hypothetisches Investitionsziel X generieren und simulieren und seine tägliche Rendite durch normale Verteilung zeichnen. Dann führen wir eine kumulative Summe durch, um den täglichen X-Wert zu erhalten.
# Generate daily returns
Xreturns = np.random.normal(0, 1, 100)
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
Xreturns), name='X')
+ 50
X.plot(figsize=(15,7))
plt.show()
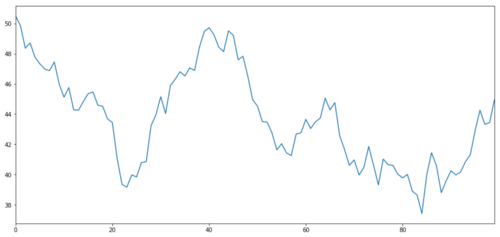
Das X des Anlageobjekts wird simuliert, um seine tägliche Rendite durch eine normale Verteilung zu ermitteln
Jetzt erzeugen wir Y, das stark mit X integriert ist, also sollte der Preis von Y sehr ähnlich sein wie die Veränderung von X. Wir modellieren dies, indem wir X nehmen, es nach oben bewegen und etwas zufälliges Rauschen hinzufügen, das aus der normalen Verteilung extrahiert wird.
noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()
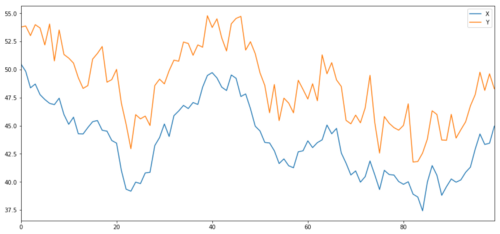
X und Y des Kointegrationsinvestitionsobjekts
Kointegration
Die Kointegration ist der Korrelation sehr ähnlich, was bedeutet, dass sich das Verhältnis zwischen zwei Datenreihen nahe dem Durchschnittswert ändert.
Y =
Wo
Für Paare, die zwischen zwei Zeitreihen handeln, muss der erwartete Wert des Verhältnisses im Laufe der Zeit zum Mittelwert konvergieren, dh sie sollten kointegriert werden. Die oben aufgebaute Zeitreihen sind kointegriert. Wir werden jetzt das Verhältnis zwischen ihnen zeichnen, damit wir sehen können, wie es aussieht.
(Y/X).plot(figsize=(15,7))
plt.axhline((Y/X).mean(), color='red', linestyle='--')
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()
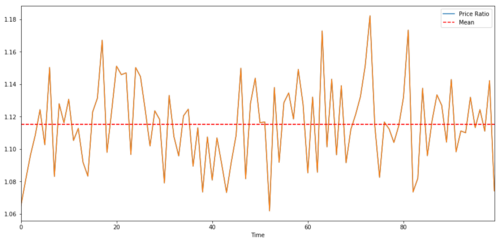
Verhältnis und Durchschnittswert zwischen zwei integrierten Zielpreisen für Investitionen
Kointegrationstest
Eine praktische Testmethode ist die Verwendung von statsmodels.tsa.stattools. Wir werden einen sehr niedrigen p-Wert sehen, weil wir zwei Datenreihen künstlich erstellt haben, die so ko-integriert wie möglich sind.
# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue
Das Ergebnis ist: 1.81864477307e-17
Anmerkung: Korrelation und Kointegration
Korrelation und Kointegration sind zwar in der Theorie ähnlich, aber nicht dasselbe. Schauen wir uns Beispiele für relevante, aber nicht kointegrierte Datenreihen an und umgekehrt.
X.corr(Y)
Das Ergebnis ist: 0,951
Wie wir erwartet hatten, ist das sehr hoch. Aber was ist mit zwei verwandten, aber nicht ko-integrierten Reihen? Ein einfaches Beispiel ist eine Reihe von zwei abweichenden Daten.
ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)
s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')
pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)
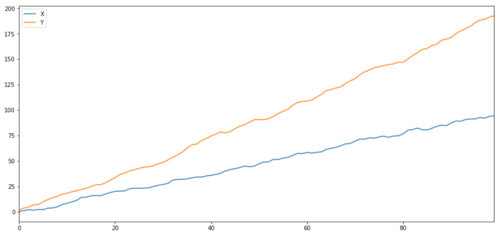
Zwei zusammenhängende Reihen (nicht miteinander integriert)
Korrelationskoeffizient: 0,998 P-Wert der Kointegrationsprüfung: 0,258
Einfache Beispiele für eine Kointegration ohne Korrelation sind normale Verteilungssequenzen und quadratische Wellen.
Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)
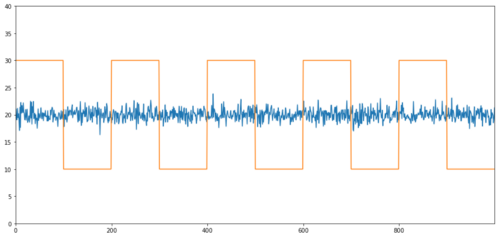
Korrelation: 0,007546 P-Wert der Kointegrationsprüfung: 0,0
Die Korrelation ist sehr gering, aber der p-Wert zeigt eine perfekte Kointegration!
Wie wird der Handel mit Paaren durchgeführt?
Da zwei zusammen integrierte Zeitreihen (z. B. X und Y oben) einander gegenüberstehen und voneinander abweichen, ist manchmal der Basis-Spread hoch oder niedrig. Wir führen den Paarhandel durch, indem wir ein Anlageobjekt kaufen und ein anderes verkaufen. Auf diese Weise, wenn die beiden Anlageziele zusammen fallen oder steigen, werden wir weder Geld verdienen noch Geld verlieren, dh wir sind neutral auf dem Markt.
Zurück zu oben, X und Y in Y =
Das ist, wenn das Verhältnis
sehr klein ist und wir erwarten, dass es zunimmt. Kurzverhältnis: Dies ist, wenn das Verhältnis
sehr groß ist und wir erwarten, dass es abnimmt.
Bitte beachten Sie, dass wir immer eine "Hedge-Position" haben: Wenn das Handelsobjekt einen Verlustwert kauft, wird die Short-Position Geld verdienen, und umgekehrt, so dass wir immun gegen den allgemeinen Markttrend sind.
Wenn sich die X und Y des Handelsobjekts relativ zueinander bewegen, werden wir Geld verdienen oder Geld verlieren.
Verwenden Sie Daten, um Handelsobjekte mit ähnlichem Verhalten zu finden
Der beste Weg, dies zu tun, besteht darin, mit dem Handelsobjekt zu beginnen, von dem Sie vermuten, dass es sich um eine Kointegration handelt, und einen statistischen Test durchzuführen.Mehrfachvergleichsverzerrung.
Mehrfachvergleichsverzerrungbezieht sich auf die erhöhte Wahrscheinlichkeit, dass beim Ausführen vieler Tests wichtige p-Werte falsch generiert werden, da wir eine große Anzahl von Tests ausführen müssen. Wenn wir 100 Tests mit zufälligen Daten ausführen, sollten wir 5 p-Werte unter 0,05 sehen. Wenn Sie n Handelsziele für die Kointegration vergleichen möchten, führen Sie n (n-1) /2-Vergleiche durch und Sie werden viele falsche p-Werte sehen, die mit der Zunahme Ihrer Testproben zunehmen. Um diese Situation zu vermeiden, wählen Sie ein paar Handelspaare aus und Sie haben Grund zu bestimmen, dass sie Kointegration sein können, und testen sie dann separat. Dies wird erheblich reduzierenMehrfachvergleichsverzerrung.
Daher versuchen wir, einige Handelsziele zu finden, die eine Kointegration zeigen. Nehmen wir als Beispiel einen Korb großer US-amerikanischer Technologieaktien im S&P 500 Index. Diese Handelsziele arbeiten in ähnlichen Marktsegmenten und haben Kointegrationspreise. Wir scannen die Liste der Handelsobjekte und testen die Kointegration zwischen allen Paaren.
Die zurückgegebene Matrix für den Kointegrationstest, die Matrix für den p-Wert und alle Paare mit einem p-Wert von weniger als 0,05.Diese Methode ist anfällig für mehrfache Vergleichsverzerrungen, so dass sie tatsächlich eine zweite Überprüfung durchführen müssen.In diesem Artikel wollen wir diesen Punkt des Beispiels aus Gründen der Bequemlichkeit unserer Erklärung ignorieren.
def find_cointegrated_pairs(data):
n = data.shape[1]
score_matrix = np.zeros((n, n))
pvalue_matrix = np.ones((n, n))
keys = data.keys()
pairs = []
for i in range(n):
for j in range(i+1, n):
S1 = data[keys[i]]
S2 = data[keys[j]]
result = coint(S1, S2)
score = result[0]
pvalue = result[1]
score_matrix[i, j] = score
pvalue_matrix[i, j] = pvalue
if pvalue < 0.02:
pairs.append((keys[i], keys[j]))
return score_matrix, pvalue_matrix, pairs
Anmerkung: Wir haben die Marktbenchmark (SPX) in die Daten aufgenommen - der Markt hat den Fluss vieler Handelsobjekte getrieben. Normalerweise können Sie zwei Handelsobjekte finden, die zusammen integriert zu sein scheinen; In Wirklichkeit integrieren sie sich jedoch nicht untereinander, sondern mit dem Markt. Dies wird als verwirrende Variable bezeichnet. Es ist wichtig, die Marktbeteiligung in jeder Beziehung zu überprüfen, die Sie finden.
from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
dataSetId=dataSetId,
instrumentIds=instrumentIds,
startDateStr=startDateStr,
endDateStr=endDateStr,
event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Jetzt versuchen wir, unsere Methode zu verwenden, um kointegrierte Handelspare zu finden.
# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds,
yticklabels=instrumentIds, cmap=’RdYlGn_r’,
mask = (pvalues >= 0.98))
plt.show()
print pairs
[('ADBE', 'MSFT')]
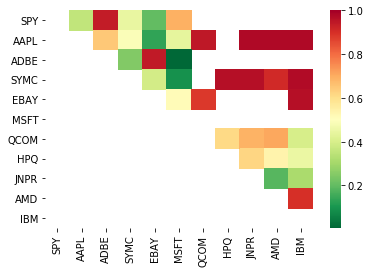
Es sieht so aus, als wären
S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()
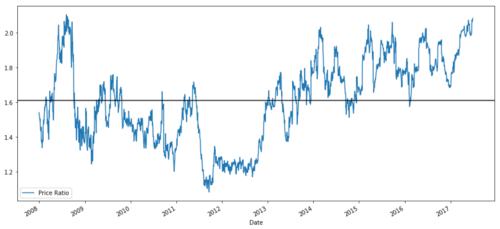
Tabelle des Preisverhältnisses zwischen MSFT und ADBE von 2008 bis 2017
Diese Ratio sieht aus wie ein stabiler Durchschnitt. Absolute Verhältnisse sind nicht statistisch nützlich. Es ist hilfreicher, unsere Signale zu standardisieren, indem wir sie als Z-Score behandeln.
Z-Score (Wert) = (Wert
Warnung
In der Tat versuchen wir in der Regel, die Daten unter der Prämisse zu erweitern, dass die Daten normal verteilt sind. Allerdings sind viele Finanzdaten nicht normal verteilt, so dass wir sehr vorsichtig sein müssen, nicht einfach Normalität oder eine bestimmte Verteilung anzunehmen, wenn wir Statistiken erstellen. Die wahre Verteilung von Verhältnissen kann einen Fat-Tail-Effekt haben, und diese Daten, die dazu neigen, extrem zu sein, werden unser Modell verwirren und zu riesigen Verlusten führen.
def zscore(series):
return (series - series.mean()) / np.std(series)
zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()
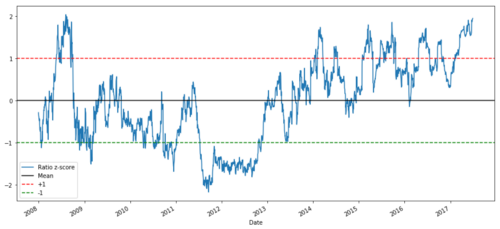
Z-Preisverhältnis zwischen MSFT und ADBE von 2008 bis 2017
Nun ist es einfacher, die Bewegung des Verhältnisses in der Nähe des Durchschnittswerts zu beobachten, aber manchmal ist es leicht, einen großen Unterschied zum Durchschnittswert zu haben.
Nun, da wir die Grundkenntnisse der Pair-Trading-Strategie diskutiert haben und den Gegenstand der gemeinsamen Integration auf der Grundlage des historischen Preises bestimmt haben, versuchen wir, ein Handelssignal zu entwickeln.
Zuverlässige Daten sammeln und Daten bereinigen;
Erstellen von Funktionen aus Daten zur Identifizierung von Handelssignalen/Logik;
Funktionen können gleitende Durchschnitte oder Preisdaten, Korrelationen oder Verhältnisse komplexerer Signale sein - diese können kombiniert werden, um neue Funktionen zu erzeugen;
Verwenden Sie diese Funktionen, um Handelssignale zu generieren, d. h. welche Signale kaufen, verkaufen oder welche Short-Positionen zu beobachten sind.
Glücklicherweise haben wir die FMZ Quant Plattform (fmz.com), die uns die oben genannten vier Aspekte erledigt hat, was für Strategieentwickler ein großer Segen ist.
In der FMZ Quant-Plattform gibt es verkapselte Schnittstellen für verschiedene Mainstream-Börsen. Was wir tun müssen, ist diese API-Schnittstellen zu nennen. Der Rest der zugrunde liegenden Implementierungslogik wurde von einem professionellen Team fertiggestellt.
Um die Logik zu vervollständigen und das Prinzip in diesem Artikel zu erklären, werden wir diese zugrunde liegenden Logiken im Detail vorstellen.
Fangen wir an:
Schritt 1: Stellen Sie Ihre Frage
Hier versuchen wir, ein Signal zu erstellen, um uns zu sagen, ob das Verhältnis im nächsten Moment kaufen oder verkaufen wird, das heißt, unsere Vorhersagevariable Y:
Y = Verhältnis ist Kauf (1) oder Verkauf (-1)
Y(t)= Zeichen(Verhältnis(t+1)
Bitte beachten Sie, dass wir nicht den tatsächlichen Transaktionszielpreis oder sogar den tatsächlichen Wert des Verhältnisses vorhersagen müssen (obwohl wir das können), sondern nur die Verhältnisrichtung im nächsten Schritt.
Schritt 2: Zuverlässige und genaue Daten sammeln
FMZ Quant ist Ihr Freund! Sie müssen nur das zu handelende Transaktionsobjekt und die zu verwendende Datenquelle angeben, und es extrahiert die erforderlichen Daten und löscht sie für Dividend- und Transaktionsobjektspaltung. Die Daten hier sind also sehr sauber.
Für die Handelstage der letzten zehn Jahre (ca. 2500 Datenpunkte) erhielten wir mit Hilfe von Yahoo Finance folgende Daten: Eröffnungspreis, Schlusskurs, höchster Preis, niedrigster Preis und Handelsvolumen.
Schritt 3: Daten aufteilen
Vergessen Sie nicht diesen sehr wichtigen Schritt bei der Prüfung der Genauigkeit des Modells.
Ausbildung 7 Jahre ~ 70%
Test ~ 3 Jahre 30%
ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]
Im Idealfall sollten wir auch Validierungsmengen erstellen, aber das tun wir jetzt nicht.
Schritt 4: Feature Engineering
Was können die damit verbundenen Funktionen sein? Wir wollen die Richtung der Verhältnisänderung vorhersagen. Wir haben gesehen, dass unsere beiden Handelsziele kointegriert sind, so dass dieses Verhältnis dazu neigt, sich zu verschieben und zum Durchschnittswert zurückzukehren. Es scheint, dass unsere Eigenschaften einige Maßnahmen des Durchschnittsverhältnisses sein sollten, und die Differenz zwischen dem aktuellen Wert und dem Durchschnittswert kann unser Handelssignal erzeugen.
Wir verwenden folgende Funktionen:
60 Tage gleitender Durchschnitt: Messung des gleitenden Durchschnitts;
5-tägige gleitende Durchschnittsquote: Messung des aktuellen Wertes des Durchschnitts;
Standardabweichung von 60 Tagen;
Z-Score: (5d MA - 60d MA) / 60d SD.
ratios_mavg5 = train.rolling(window=5,
center=False).mean()
ratios_mavg60 = train.rolling(window=60,
center=False).mean()
std_60 = train.rolling(window=60,
center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()
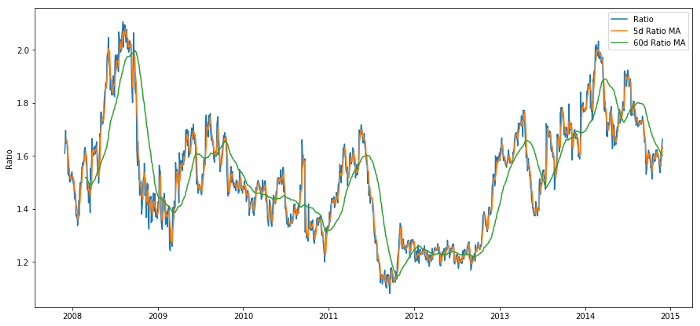
Preisverhältnis zwischen 60d und 5d MA
plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()
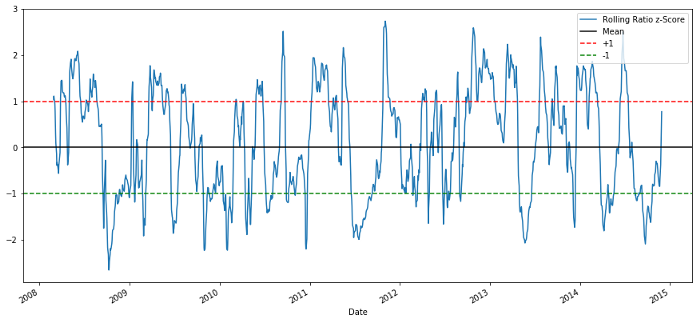
60-5 Z-Punktpreisverhältnisse
Der Z-Score des gleitenden Durchschnittswertes bringt die durchschnittliche Wertregressions-Eigenschaft des Verhältnisses hervor!
Schritt 5: Auswahl des Modells
Lassen Sie uns mit einem sehr einfachen Modell beginnen. Wenn wir uns das z-Score-Diagramm ansehen, können wir sehen, dass, wenn der z-Score zu hoch oder zu niedrig ist, er zurückkehrt. Lassen Sie uns +1/- 1 als Schwelle verwenden, um zu hoch und zu niedrig zu definieren, und dann können wir das folgende Modell verwenden, um Handelssignale zu generieren:
Wenn z unter - 1.0 liegt, ist das Verhältnis zu kaufen (1), weil wir erwarten, dass z auf 0 zurückkehrt, so dass das Verhältnis steigt;
Wenn z über 1,0 liegt, wird das Verhältnis verkauft (- 1), weil wir erwarten, dass z auf 0 zurückkehrt, so dass das Verhältnis sinkt.
Schritt 6: Schulung, Überprüfung und Optimierung
Wir werden uns die Ergebnisse dieser Studie anhand der Ergebnisse der Studie anhand der Ergebnisse der Studie ansehen.
# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()
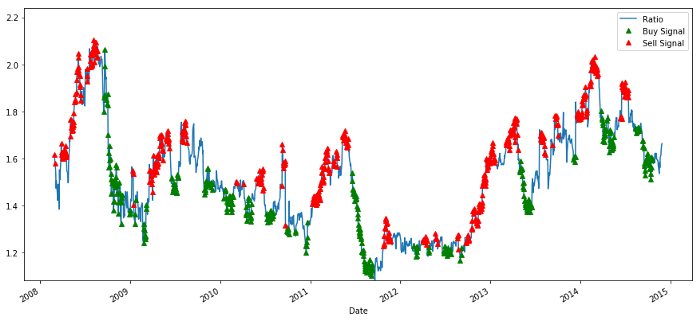
Kauf- und Verkaufspreisverhältnissignal
Das Signal scheint vernünftig zu sein. Wir verkaufen, wenn es hoch oder steigt (rote Punkte) und kaufen es zurück, wenn es niedrig ist (grüne Punkte) und sinkt. Was bedeutet das für den eigentlichen Gegenstand unserer Transaktion?
# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()
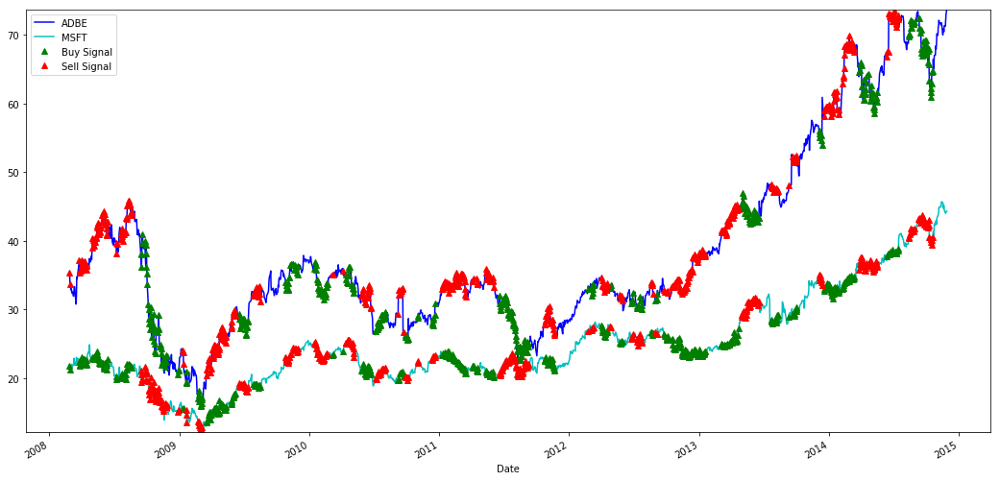
Signale zum Kauf und Verkauf von MSFT- und ADBE-Aktien
Bitte beachten Sie, wie wir manchmal mit
Wir sind mit dem Signal der Trainingsdaten zufrieden. Lassen Sie uns sehen, welche Art von Gewinn dieses Signal generieren kann. Wenn das Verhältnis niedrig ist, können wir einen einfachen Rücktest machen, ein Verhältnis kaufen (kaufen 1 ADBE-Aktie und verkaufen Verhältnis x MSFT-Aktie), und verkaufen ein Verhältnis (verkaufen 1 ADBE-Aktie und kaufen x Verhältnis MSFT-Aktie), wenn es hoch ist, und berechnen die PnL-Transaktionen dieser Verhältnisse.
# Trade using a simple strategy
def trade(S1, S2, window1, window2):
# If window length is 0, algorithm doesn't make sense, so exit
if (window1 == 0) or (window2 == 0):
return 0
# Compute rolling mean and rolling standard deviation
ratios = S1/S2
ma1 = ratios.rolling(window=window1,
center=False).mean()
ma2 = ratios.rolling(window=window2,
center=False).mean()
std = ratios.rolling(window=window2,
center=False).std()
zscore = (ma1 - ma2)/std
# Simulate trading
# Start with no money and no positions
money = 0
countS1 = 0
countS2 = 0
for i in range(len(ratios)):
# Sell short if the z-score is > 1
if zscore[i] > 1:
money += S1[i] - S2[i] * ratios[i]
countS1 -= 1
countS2 += ratios[i]
print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
# Buy long if the z-score is < 1
elif zscore[i] < -1:
money -= S1[i] - S2[i] * ratios[i]
countS1 += 1
countS2 -= ratios[i]
print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
# Clear positions if the z-score between -.5 and .5
elif abs(zscore[i]) < 0.75:
money += S1[i] * countS1 + S2[i] * countS2
countS1 = 0
countS2 = 0
print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)
Das Ergebnis ist: 1783.375
Diese Strategie scheint also profitabel zu sein! Jetzt können wir die Optimierung weiter vorantreiben, indem wir das gleitende Durchschnittszeitfenster ändern, indem wir die Schwellenwerte für Kauf/Verkauf und Schließung von Positionen ändern und die Leistungsverbesserung der Validierungsdaten überprüfen.
Wir können auch kompliziertere Modelle wie Logistic Regression und SVM ausprobieren, um 1/-1 vorherzusagen.
Lassen Sie uns nun dieses Modell vorantreiben, was uns zu:
Schritt 7: Rückprüfung der Prüfdaten
Auch hier nutzt die FMZ Quant-Plattform eine leistungsstarke QPS/TPS-Backtesting-Engine, um die historische Umgebung wahrhaft zu reproduzieren, häufige quantitative Backtesting-Fälle zu beseitigen und die Mängel von Strategien rechtzeitig zu entdecken, um die echte Bot-Investition besser zu unterstützen.
Um das Prinzip zu erklären, wird in diesem Artikel immer noch die zugrunde liegende Logik gezeigt. In der praktischen Anwendung empfehlen wir den Lesern, die FMZ Quant Plattform zu verwenden. Neben der Zeitersparnis ist es wichtig, die Fehlerverträglichkeit zu verbessern.
Das Backtesting ist einfach. Wir können die obige Funktion verwenden, um die PnL der Testdaten anzuzeigen.
trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)
Das Ergebnis ist: 5262.868
Das Modell hat einen tollen Job gemacht! Es wurde unser erstes einfaches Paar-Handelsmodell.
Vermeiden Sie eine Überanpassung
Bevor ich die Diskussion beende, möchte ich insbesondere über Überfitting sprechen. Überfitting ist die gefährlichste Falle in Handelsstrategien. Der Überfitting-Algorithmus kann im Backtest sehr gut funktionieren, aber bei den neuen unsichtbaren Daten scheitern - was bedeutet, dass er keinen Trend der Daten wirklich offenbart und keine echte Vorhersagefähigkeit hat.
In unserem Modell verwenden wir rollende Parameter, um die Zeitfensterlänge zu schätzen und zu optimieren. Wir können uns einfach entscheiden, über alle Möglichkeiten, eine angemessene Zeitfensterlänge zu iterieren und die Zeitlänge entsprechend der besten Leistung unseres Modells auszuwählen.
# Find the window length 0-254
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762],
data['MSFT'].iloc[:1762], l, 5)
for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)
('Best window length:', 40)
Wir untersuchen nun die Leistung des Modells anhand der Testdaten und stellen fest, dass die Zeitfensterlänge bei weitem nicht optimal ist.
# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:],
data['MSFT'].iloc[1762:],l,5)
for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset,
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])
(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)
Es ist offensichtlich, daß die für uns geeigneten Stichprobendaten in Zukunft nicht immer gute Ergebnisse liefern.
plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()
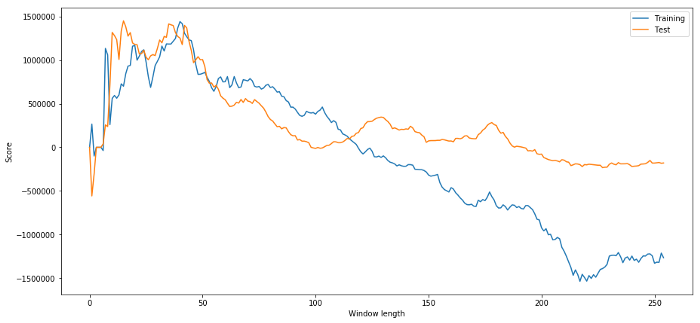
Wir können sehen, dass alles zwischen 20 und 50 eine gute Wahl für Zeitfenster ist.
Um eine Überanpassung zu vermeiden, können wir wirtschaftliche Argumente oder die Art des Algorithmus verwenden, um die Länge des Zeitfensters auszuwählen.
Der nächste Schritt.
In diesem Artikel schlagen wir einige einfache Einführungsmethoden vor, um den Prozess der Entwicklung von Handelsstrategien zu demonstrieren.
Hurst-Exponent;
Halbwertszeit der mittleren Regression, abgeleitet aus dem Ornstein-Uhlenbeck-Verfahren;
Kalman-Filter.
- Quantitative Praxis der DEX-Börsen (2) -- Benutzerhandbuch für Hyperflüssigkeiten
- DEX-Börsen Quantitative Praxis ((2) -- Hyperliquid Benutzerhandbuch
- Quantitative Praxis der DEX-Börsen (1) -- dYdX v4 Benutzerhandbuch
- Einführung in Lead-Lag-Arbitrage in Kryptowährungen (3)
- DEX-Börsen Quantitative Praxis ((1)-- dYdX v4 Benutzerhandbuch
- Einführung der Lead-Lag-Suite in der Kryptowährung (3)
- Einführung in Lead-Lag-Arbitrage in Kryptowährungen (2)
- Einführung der Lead-Lag-Suite in der digitalen Währung (2)
- Diskussion über den externen Signalempfang der FMZ-Plattform: Eine Komplettlösung für den Empfang von Signalen mit integriertem Http-Service in der Strategie
- FMZ-Plattform: Erforschung von Signalempfangsstrategien für externe Netzwerke
- Einführung in Lead-Lag-Arbitrage in Kryptowährungen (1)
- Neuronale Netzwerke und Quantitative Trading in digitaler Währung (2) - Intensives Lernen und Schulen Bitcoin Trading Strategie
- Neuronale Netzwerke und digitale Währung Quantitative Trading Series (1) - LSTM prognostiziert Bitcoin Preis
- Anwendung der Kombinationsstrategie von SMA und RSI Relative Strength Index
- Entwicklung der CTA-Strategie und der Standardklassenbibliothek der FMZ Quant-Plattform
- Quantitative Handelsstrategie mit Preisdynamikanalyse in Python
- Implementieren Sie eine Dual-Push-Quantitative Trading-Strategie für digitale Währungen in Python
- Der beste Weg zum Installieren und Upgrade für Linux Docker
- Erreichung einer ausgewogenen Eigenkapitalstrategie mit einer ordnungsgemäßen Ausrichtung von Long-Short-Positionen
- Zeitreihendatenanalyse und Tick-Daten-Backtesting
- Quantitative Analyse des Marktes für digitale Währungen
- Anwendung der Maschinellen Lerntechnologie im Handel
- Nutzung des Forschungsumfelds zur Analyse der Einzelheiten der dreieckigen Absicherung und der Auswirkungen der Abwicklungsgebühren auf die abgesicherten Preisdifferenzen
- Reform der Deribit-Futures-API zur Anpassung an den quantitativen Handel mit Optionen
- Bessere Werkzeuge machen gute Arbeit - lernen Sie, die Forschungsumgebung zu verwenden, um Handelsprinzipien zu analysieren
- Währungsübergreifende Absicherungsstrategien beim quantitativen Handel mit Blockchain-Assets
- Erwerben Sie den Leitfaden zur Digitalwährungsstrategie von FMex auf FMZ Quant
- Ich lehre Sie Strategien zu schreiben - eine MyLanguage-Strategie transplantieren (Advanced)
- Sie lernen, Strategien zu schreiben -- transplantieren Sie eine MyLanguage-Strategie
- Sie lernen, Multi-Chart-Unterstützung der Strategie hinzuzufügen
- Lehren Sie, eine K-Linie Synthese-Funktion in der Python-Version zu schreiben