Handelsstrategie für polarisierte Fraktalleffizienz (PFE)

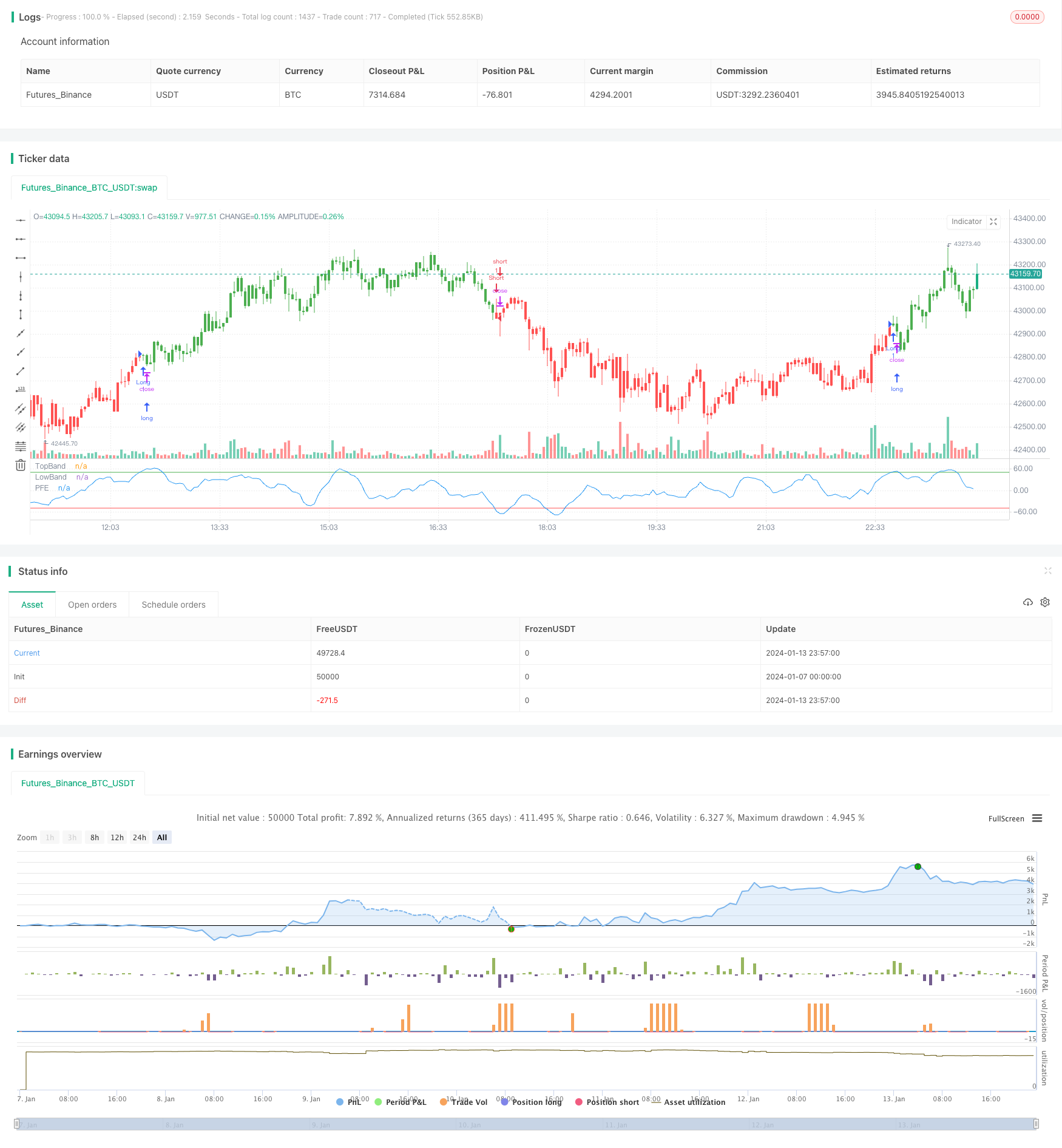
Übersicht

Die Polarisierte Fraktal-Effizienz (PFE) -Handelsstrategie misst die Effizienz von Preisbewegungen, indem sie Konzepte aus Fraktalgeometrie und Chaostheorie anwendet. Je linearer und effizienter die Preisbewegung ist, desto kürzer ist die Entfernung, die die Preise zwischen zwei Punkten zurücklegen, und desto höher ist die Effizienz.

Strategie Logik

Der Kernindikator der PFE-Handelsstrategie ist die polarisierte Fraktalwirksamkeit (PFE), die auf der Grundlage der folgenden Formel berechnet wird:

PFE = sqrt(pow(close - close[Length], 2) + 100)

PFE misst im Wesentlichen die länge der Preisbewegung über den Zeitraum der Länge, wobei die euklidische Entfernung (Gleichlinienentfernung) als Annäherung verwendet wird.

Um die Effizienz der Preisbewegung zu bewerten, benötigen wir einen Vergleichswert, der die Länge des Pfades darstellt, der die Preise über einen Zeitraum von Länge nach der tatsächlichen Reihenfolge verbindet, die C2C (Close to Close) genannt wird und wie folgt berechnet wird:

C2C = sum(sqrt(pow((close - close[1]), 2) + 1), Length)

So können wir die Fraktal-Effizienz der Preisbewegung xFracEff berechnen:

xFracEff = iff(close - close[Length] > 0, round((PFE / C2C) * 100) , round(-(PFE / C2C) * 100))

Der positive Wert, wenn der Preis steigt, und der negative Wert, wenn der Preis fällt.

Um Handelssignale zu generieren, berechnen wir den exponentiellen gleitenden Durchschnitt von xFracEff, genannt xEMA.

xEMA = ema(xFracEff, LengthEMA)

BuyBand = input(50)
SellBand = input(-50)  

Wenn xEMA über BuyBand kreuzt, erzeugt es ein Kaufsignal. Wenn es unter SellBand kreuzt, erzeugt es ein Verkaufssignal.

Analyse der Vorteile

Die PFE-Handelsstrategie weist folgende Vorteile auf:

1. Anwendet einzigartige Konzepte aus der Fraktalgeometrie und der Chaostheorie, um die Effizienz der Preisbewegung aus einem anderen Blickwinkel zu messen
2. Vermeidet einige Probleme herkömmlicher technischer Indikatoren wie Kurvenanpassung
3. Die Parameter können angepasst werden, um geeignete Einstellungen für verschiedene Marktumgebungen zu finden
4. Einfache und klare Handelsregeln, die leicht umzusetzen sind

Risikoanalyse

Die PFE-Handelsstrategie birgt außerdem folgende Risiken:

1. Schwierige Optimierung von Parametern, anfällig für Überanpassung wie alle Indikatorstrategien
2. Unzuverlässige Signale bei extremen Turbulenzen auf dem Markt
3. Es muss mit Vorsicht mit Extremen wie Preisspalten umgehen.
4. Verpassen Sie einen gewissen Zeitverzug, vielleicht haben Sie den besten Einstiegspunkt verpasst, wenn das Signal auslöst

Optimierungsrichtlinien

Die PFE-Strategie kann in folgenden Aspekten optimiert werden:

1. Versuchen Sie verschiedene Kombinationen des Parameters Länge, um ein optimales Gleichgewicht zu finden
2. Optimierung der Kauf- und Verkaufsbänder zur Verringerung fehlerhafter Transaktionen
3. Hinzufügen von Stop Loss zur Kontrolle der Größe eines einzelnen Handelsverlusts
4. Kombination anderer Indikatoren zur Verbesserung der Signalqualität
5. Dynamische Anpassung der Parameter an sich ändernde Marktbedingungen

Zusammenfassung

Die PFE-Handelsstrategie schlägt einen neuartigen Ansatz vor, der auf Fraktalgeometrie und Chaos-Theorie-Konzepten basiert, um die Effizienz von Kursbewegungen zu messen. Im Vergleich zu herkömmlichen technischen Indikatoren hat diese Methode ihre einzigartigen Vorteile, hat aber auch Probleme wie Zeitverzögerung, Parameteroptimierung, Signalqualität bis zu einem gewissen Grad.