Talk about how to optimize the parameters of several programmatic trading models.
Author: Inventors quantify - small dreams, Created: 2017-09-27 11:38:08, Updated: 2017-09-27 11:39:08Talk about how to optimize the parameters of several programmatic trading models.
- ### Parameter plateaus and Parameter islands What do you mean? An important principle in parameter optimization is to aim for a parameter plateau rather than a parameter island. The so-called parameter plateau refers to the existence of a wider range of parameters within which the model can perform better, generally forming an approximate normal distribution at the center of the plateau. The so-called parameter island refers to the fact that the model performs better only when the parameter value is within a very small range, and when the parameter deviates from this value, the model expression will vary significantly.
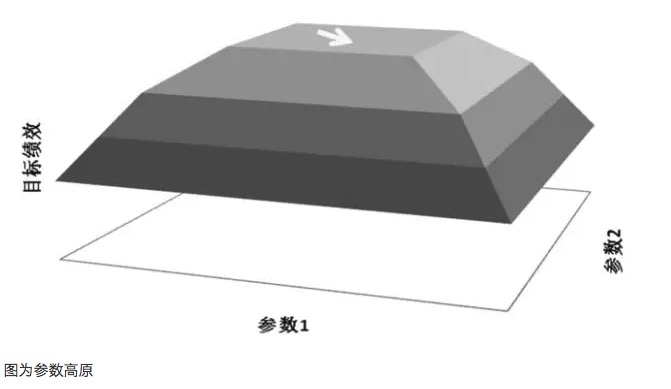
- #### The graph is a parameter plateau
For example, if a trading model has two parameters, parameters 1 and 2, a three-dimensional performance map is obtained when both parameters are tested. A good parameter distribution should be a parameter plateau plot, and even if the parameters are deviated, the model's profit performance can still be guaranteed. Such parameters, due to their stability, can make the model more resilient when it encounters all kinds of trades in the future real world.
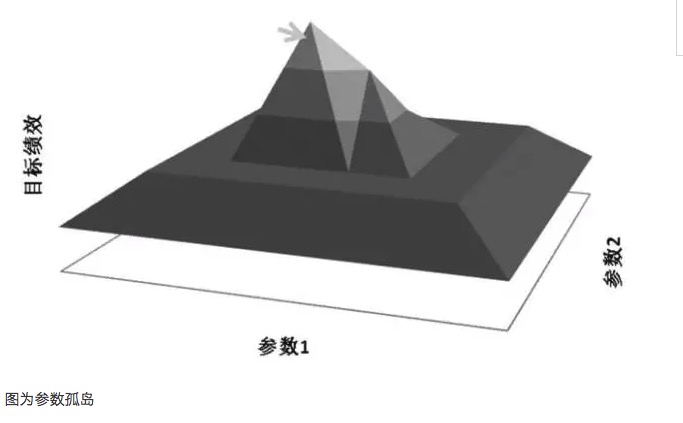
In general, if the nearest parameter system performs much less well than the optimal parameter, then the optimal parameter may be a result of over-simplification, which can be considered mathematically as a singularity solution rather than the extreme value solution to be sought. From a mathematical point of view, the singularity is unstable, and in future uncertainties, once the market characteristics change, the optimal parameter may become the worst parameter.
Overfitting is associated with the sample being selected, where if the sample is not representative of the overall characteristics of the market, the parameters are adjusted only in order to make the test result positive to the expected value. This is undoubtedly self-deception, and the resulting parameter value is the invalid parameter value of overfitting. For example, by analyzing the parameters overfitting, the trading model shows a phenomenon of surge in yields at values 35 and 63 respectively.
The main contradiction between overfit and parameter optimization is that the optimal parameters for model parameters are based on samples of historical data that have already occurred, while the future market is dynamically changing, with both similarities and variations compared to the historical market. The model designer can find the parameters that the model performs best in history, but this parameter may not perform the best in the actual application of the model in the future, much less the parameters that perform best in the actual application of the model in the future.
In addition, the parameter plateau and the parameter islands often have a greater relationship to the number of trades. If the number of trades in the model is small, it is often possible to find a suitable parameter point that makes the model profitable in all of these trades, and this parameter-optimized model gain reflects a stronger randomness. If the number of trades in the model is large, the randomness of the model gain decreases, and there is also a parameter plateau that more reflects the inevitability and regularity of the gain.
- #### How to optimize parameters
After understanding the parametric plateau and the parametric islands, it is important to optimize parameters, especially when there are multiple parameters in the model (hereinafter referred to as parameter sets), often the value of one parameter affects the distribution of another parameter plateau. So how to optimize the parameter set?
One method is the stepwise convergence method; i.e. first one parameter is optimized separately, its optimum value is obtained and then fixed, and then the other parameter is optimized and then fixed. This loop continues until the optimization results no longer change. For example, a homogeneous cross-border trading model, where the two independent parameters are the median short cycle N1 and the long cycle N2 respectively. N2 is first fixed at 1, N1 is tested on a range of values from 1 to 100, the optimum value is found and finally fixed at 8; N2 is optimized from 1200 to 26, the optimum value is finally fixed; N1 is optimized again for a second round, the new optimum value is fixed at 10; N2 is optimized and finally fixed at 28.
Another method is to use a programmatic software design platform with stronger computational capabilities to directly calculate the distribution between the target function and the parameter set, and then to search for a multi-dimensional differential distribution, defining a differential threshold, the absolute value of the difference is less than the threshold range corresponding to the largest multi-dimensional volume, the largest multi-dimensional inner sphere radius, selected as the most stable parameter value.
In addition to the parametric optimization method, data sample selection is also an important factor. Models with trend-following trading ideas perform better when trending markets emerge, and strategies with high-selling, low-buying trading ideas perform better in volatile markets. Therefore, when optimizing parameters, it is necessary to properly filter out markets that match trading ideas to consider profits, and to add market data that does not match trading ideas to consider losses.
For example, in the early 2010s, when the stock market was listed, and in the second half of 2014, when the extreme bull market emerged, stock futures have been a one-sided market. There is no doubt that all trend models will have a good effect. However, if we also put this extreme market data into the sample for parameter optimization, the model parameters we get may not be the best.
For example, suppose a model has two parameters, one of which performs very well in the one-sided market time period and performs generally in other time periods; the other of which performs less well in the one-sided market time period and performs better in other time periods, and the distribution of parameters A is more even between the time periods. Even if parameters A and B are preferred because of the relative stability of the parameters B and B, even if the overall indicators of the test of the entire sample data, such as the risk-reward ratio, are higher than those of the B parameter.
In summary, when building a programmatic trading model, on the one hand, it is possible to optimize the model by parameters, so that the model is better adapted to the pattern of price fluctuations and improves investment returns; on the other hand, it is necessary to prevent over-fitting of the parameters, which leads to a significant reduction in the applicability of the model to market changes.
Translated from Programmatic Trader
- How do you make gold forks?
- Built-in function_Cross analysis and instructions
- “Plan expired” while I never bought a plan…
- How do we get data from decentralized exchanges?????
- Digital currency price monitoring analysis real-time analysis Bitcoin and Bitfinex failed to operate successfully
- Poloniex has reported an error?Error: (Exchange_Register): platformId: 27, currency: BTC_ETC, Msg: Peroid does not support Register FILE: 803 reg FILE:1264
- How to get the serial number of a specific exchange?
- But we have to look at it from a different perspective.
- In the review, did the yield curve not include the cost of the purchase?
- Catching insects, predicting the earnings, the commentary in the questionnaire is wrong
- Please teach me how to quantify the inventor's drawing, where the horizontal coordinates are not the time axis, but rather a column graph or a folded graph of numbers.
- The problem with OKEX is growing.
- It's a must to learn how to go abroad!
- Clearing up some misconceptions about transaction volume
- I'm not sure if you have time for a technical analysis of the market.
- 10 facts you need to know about machine learning
- Is there a similar community of inventors quantified abroad?
- Fed VS Bitcoin, after all, is a game of power
- Please teach: Explanation of the Profit of the Position returned by the GetPosition function
- Do you want to know how to predict the future?