Selection of timing strategy ((1) Construction of low delay trend line when Z conversion angle is selected

A few moments ago, someone in the background said that I develop a dog strategy every day, yes, dog strategy is over. Today I share with you a dog's most recent timing strategy (doge).A. The premise ● Let's get serious, the classic timing strategies are actually divided into several categories: short-term event-driven (in the coin circle, it is shown as monitoring announcements and tweets on major exchanges, involving text analysis), statistical regression and prediction (statistical arbitrage, matching trades, various ML and DL models, hierarchical Markov, etc.), GSISI type when choosing investor sentiment, and when choosing traditional classic technical indicators.

N日移动平均线=N日收盘价之和/N

● This is commonly referred to by investors as a straight line (MA), a straight line that breaks the buy, breaks the sell, and countless *beans contribute their own transaction fees to the exchange. However, there are some problems with the use of the equator for ordinary investors: first, the equator is severely delayed, and the trend is often halfway through when the signal is displayed, and the trend returns to the face; second, ordinary investors in the coin circle tend to operate on the index in fractional scale, 15, 5 minutes, or even 1 minute, in such a small period, the characteristic of the coin circle is more than 80% of the oscillations (the kind Martin likes), the trend rarely occurs, and investors lose a lot of procedural fees and slippage points to open the position according to the equator. • This paper aims to construct an algorithm for filtering equilinear indicators to reduce their latency for reference and use.

2. Z-conversion, passing function ● Prior to this article, I learned about the filter algorithms for indicators on various major websites, such as the most common silicon filter (which appears in several CTAs in Squirrel Broadcast) and the Carlman filter method studied by the author on joinquant, which successfully avoided the 2015 stock crash in retesting. The ER filter module on TB is extremely convenient to use. However, when I discovered that the Carlman filter module provided on joinquant does not load into the server, and it has thousands of lines of open source code, Apple abandoned the attempt to port it to the coin circle. ● The Z-conversion from Laplace is commonly used in the field of mathematical signal processing. For a discrete time sequence f ((k) and z defined in the multi-frequency domain, its formula is defined as follows: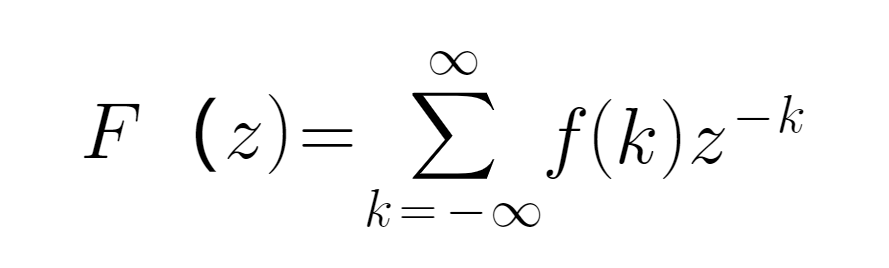

● The EMA has a lower latency than the MA (which is essentially the result obtained after processing the MA sequence using the EWMA algorithm), so we use the EMA sequence instead of the MA to improve the filter effect. We define the input as the price of the coin (which is written as p) and the output as the EMA indicator corresponding to the price (which is written as EMA).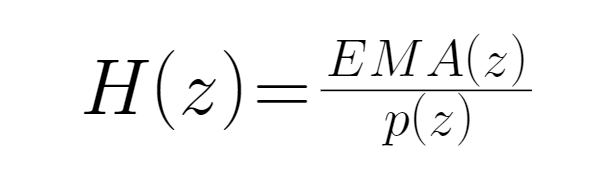

● Insert this formula into the EWMA algorithm to obtain the initial pass function of the EMA: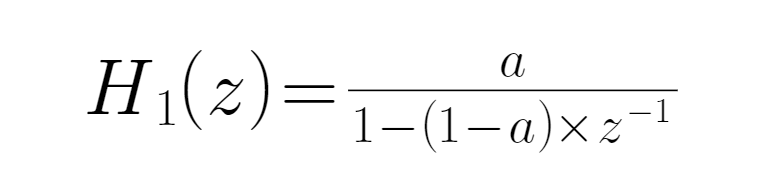

● wherein a is a variable parameter, the following equation.

C. Analysis of the passing function ● In the transmission function, the input signal is not correlated to the function value. By analyzing this function, it is known that when z**-1=-1, H(z) takes the maximum value, which is when the highest frequency is reached, the transmission function is H(z) = a/(2-a), and the noise of recent high-frequency data is maximized; when z**-1=1, H(z) is a constant, at which time the system frequency is 0, the input and the output results are exactly the same, if the time sequence is a constant sequence, then EMA will be here. ● When H (((z) is a low-pass filter, and H (((z) = 1, the output signal contains all the components of the input signal, that is, of the entire output signal, if all the low-frequency signals are subtracted, 1 - H ((z) can be constructed into a new filter, written as H 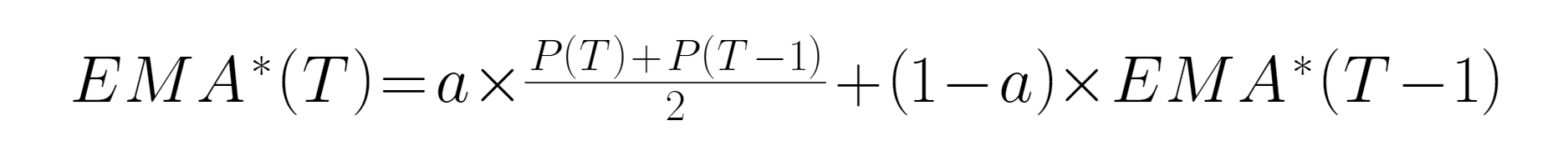((z), which is the exact opposite of H ((z), which is a high-pass filter. ● Note P(T) as the price of the coin as the root k line, we take the price of the day and the price of the previous day to smooth out this functional relation, thus making a further correction to the output EMA. This is because the original transmission function H(z) = a/(2-a, when the high-frequency signal is not effectively filtered, so a value is taken first to smooth it, if the effect is still bad, several more weightings can be taken, so the EMA correction expression entered on the day is:● This expression for low-pass filter and high-pass filter only needs to be subtracted by 1: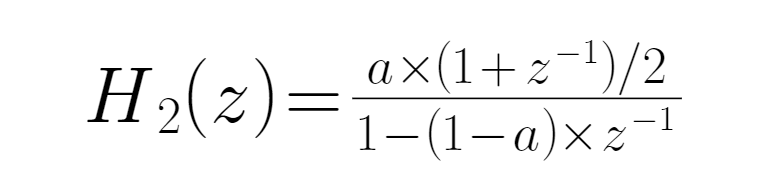● Now the expression of the filter has been constructed! With the Z transformation, we can construct a low-latency trendline with only one parameter a, the larger the a, the lower the latency, the better the smoothness. For different varieties, there are different optimal parameters.

4. Summary and notes ● The filter constructed in the above steps is only one stage, and its filter effect is not very ideal because the transition band is too long, and after increasing the stage, the complexity of the expression of the H ((z) function shows an exponential increase, and too high a stage is also prone to the occurrence of irregular jumps in the filter uniform. From past experience, stages 2 or 3 are more suitable stages, and the reader can also use a linear combination to serialize several filters of the same or different stages to observe the effect, which cannot be verified one by one because the author is busy with public affairs. ● This Z-conversion-based filter algorithm is not only applicable to indicators of the uniform linear type, all indicators with false signals, such asboll andatr, can be filtered through the filter algorithm to achieve a certain filtering effect, which determines the size of the threshold for opening positions, thereby reducing the serious aftermath of the delay of the original indicator. • This article ends with a paragraph where the author does not have time to provide the code for the algorithm, but just gives an idea that interested readers can try out for themselves.

● Promise Quant Minos focuses on the development of all kinds of fantastic groundhogs strategies with Martin at its core, for example if you have a rental need or a large capital management need, you can contact vx:15001733415