The price difference between the sale and the sale of cabbage in the first test of the EKOP model
Author: Inventors quantify - small dreams, Created: 2017-06-16 18:42:26, Updated: 2017-06-16 18:46:26The price difference between the sale and the sale of cabbage in the first test of the EKOP model
- #### ## 1 The foreword
It's been unusually busy lately, and it's been months since my last column. A lot has happened over the past few months, some of which have been unforgettable black swans in my own life. But these experiences have taught me that life, like a transaction, is up and down, full of unknowns. We always hope to be able to learn something from what has happened and slowly get closer to the truth that may not exist.
The EKOP model [1] was originally proposed to study whether the behavior of traders with different information is the cause of the difference in the price of the two types of stocks. In this column, I will explain the basis of this model. In the following article, I will do further analysis of the application of the model. The simplicity of the mathematical model presented in this paper is brilliant.
- ##### 2 Assumptions about the transaction process
When we talk about a financial model, the most important thing is to pay attention to the assumptions of the model. Good financial models have their own assumptions: it is not so strong that it is not universal; it is not so weak that it does not lead to pretty concise results. The basic assumptions of the EKOP model are:
Hypothesis 1: We are discussing the trading of stocks, the trading behaviour is discrete during the day, the trading behaviour is continuous during the day. In addition, the number of transactions that occur on a day-to-day basis varies from one day to another.
In addition, the number of transactions that occur on a day-to-day basis varies from one day to another. This is a continuous time order.
This is a continuous time order.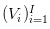 For a set of random variables that represent the stock's value at the end of each day, there are three possible scenarios for each day
For a set of random variables that represent the stock's value at the end of each day, there are three possible scenarios for each day
- If there is bad news, we write down the value of the stock as
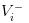
- The good news is that we're going to write down the value of the stock as:
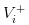
- No news, we'll write the value of the stock at
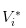
Obviously, we have.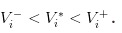
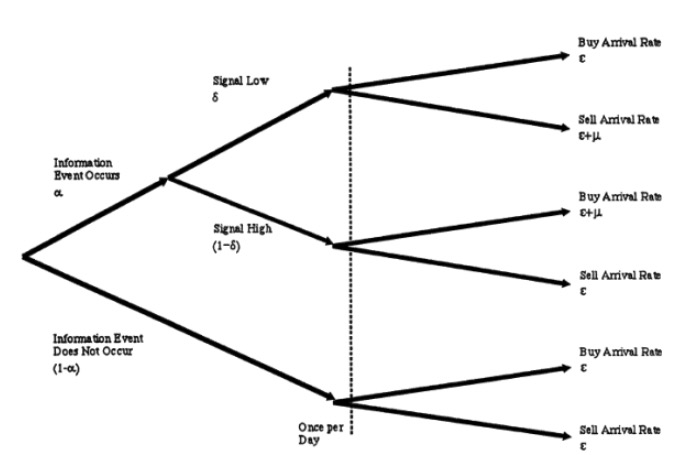
Hypothesis 2: On a given day, there is α.
There is a 1-α probability of no event affecting the stock price. On the days of the event, there is a δ probability of bad events causing the stock price to fall, and there is a 1-δ probability of good events causing the stock price to rise.
Assumption 3: Participants in stock trading are market makers (MM), informed traders (IT), and uninformed traders (UT). They follow the following trading behavior:
MM is always ready to hang a purchase or sale order for a unit, in accordance with his obligation as a market maker. MM is risk-neutral, so he hangs the order at the price he thinks is fair.
IT only trades on days when there is news, and their trading behavior is a loose process. On one day, if there is bad news, he hangs a sell order with an arrival rate of μ; and on those days when there is good news, he hangs a bill with an arrival rate of μ.
UT, that is our poor cabbage, because of the advantage of no news, their trading behavior is also a lax process, every day, they are hanging invoices and sales orders at the arrival rate ε. Note that all of the Parsons processes here are independent of each other. We can represent the 3 hypothesis in a diagram as follows.
- #### 3 Updates on deals and prices
We know that market makers are usually the big companies who are bullish and flashy. They are smart, and in the long run they have been struggling with IT and UT, and they have summarized all the model parameters in this tree diagram above through a lot of historical data analysis. But, well, they are not as strong as the knowledgeable traders, and when a certain trading day is about to open, they are not as knowledgeable as the knowledgeable traders, and they are not as keen on whether something big happens today. What they can do is, in the course of this trading day, constantly update themselves through the behavior of other traders, constantly updating themselves on what happened today, whether it was a good or bad guess.
Now, let's experience the role of an MM, fighting against IT and UT. At a certain point in time, t, we write down our guess as a vector for the probability of nothing, good, and bad happening.
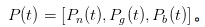 It's obvious that at the very beginning of the day, that is,
It's obvious that at the very beginning of the day, that is, So all I can do is assume that the probability of nothing happening is α and the probability of something good happening is α.
So all I can do is assume that the probability of nothing happening is α and the probability of something good happening is α.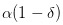 And the probability of bad things happening is
And the probability of bad things happening is
How should we update this probability? Well, we who are marketers know the Bayesian formula. In the case where we observe a sales order coming in, we use Bayesian law to update our probability estimate.
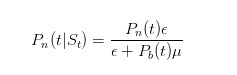
The molecule of this formula is that only uninformed traders will sell orders with ε when there is no news; while the denominator is that at any given time, uninformed traders will sell orders with ε, while informed traders will only sell orders with μ when bad things happen. Similarly, we can push forward
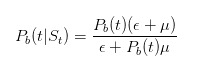
and
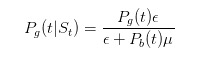
Before we continue with the inference, let's do some simple tests. We just said that if we see a sell order, then our estimate of the probability of something bad happening should be bigger.
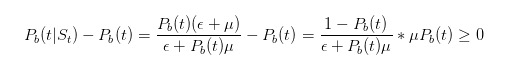
In this way, our inference confirms our intuition.
And then, once we have the updated probabilities, we can calculate the fair price, which is the price we're going to buy in the market, which is expressed as

By a similar inference, we can find that when an invoice comes in, we as market makers should be selling at a price that is
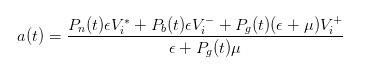
- ####4 The price difference expression after the price change
The above expression for the buy and sell price is not yet intuitive enough, we can introduce the expected value of the stock at time t to simplify the expression.

So we can convert the bid and ask expressions to
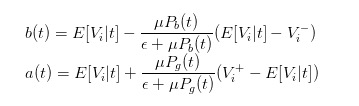
So we can express the price difference very clearly as
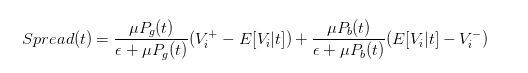
- ##### 5 The effect of traders' behavior on price differentials
With the spread expression, we can analyze the effect of different traders on the spread.
The more cabbage, the smaller the price difference. Note that ε is the arrival rate of the uninformed traders (let's call them cabbage soup) and if there is ε >> μ, we can find that the number of arrivals of the uninformed traders (let's call them cabbage soup) is the same as the number of arrivals of the uninformed traders.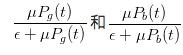 Both of these things will tend to zero, which means that the spread will also tend to zero.
If we go to the other extreme, assuming there is no more cabbage in the market, only a group of more knowledgeable traders, then we will tragically find that the price we posted will be:
Both of these things will tend to zero, which means that the spread will also tend to zero.
If we go to the other extreme, assuming there is no more cabbage in the market, only a group of more knowledgeable traders, then we will tragically find that the price we posted will be: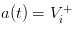 and
and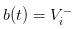 In this way, the knowledgeable traders find that they will not be profitable in any way, and the market will inevitably die down (which reminds me of the domestic commodity options market).
In this way, the knowledgeable traders find that they will not be profitable in any way, and the market will inevitably die down (which reminds me of the domestic commodity options market).
You see, based on some assumptions, using very simple mathematical deductions, we were able to come to this interesting and profound conclusion, which is probably the great charm of the mathematical model.
[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.
- How to customize the set of currencies not shown on the exchange label when creating a digital currency trading robot
- The LogStatus function shown in the Python interface
- The LogStatus function shown in the Python interface
- Exchange fee summary
- Project templates that write their own TypeScript policies, need to be customizable
- Inventors Quantify: Is the editor theme available for download?
- Settings for remittance fees
- TableTemplet Template for the status bar of the table (note)
- Problems encountered when retrieving K-line data in real-time with GetRecords after switching transactions
- Introduce a local edit policy for the vscode plugin to automatically sync to the server
- Bitcoin automated trading commissioned
- About the exchange.GetName
- What is the digital currency buy function?
- Calling for Group
- Build an interactive button function in the policy status bar
- Questions about fees
- There seems to be a minor bug on the platform.
- Digital currency: the function of currency pairs
- YY please if the status interface can add a button.
- It seems that there are few high-frequency strategies on our platform, and there are no better high-frequency open source strategies besides the Cabbage Harvester.
louisThe sad conclusion