Bayes - the mystery of decoding probability, exploring the mathematical wisdom behind decision making

Bayesian statistics is a strong university discipline in the field of mathematics, with a wide range of applications in many fields, including finance, medical research, and information technology. It allows us to combine previous beliefs with evidence to derive new post-concept beliefs that enable us to make more informed decisions.

In this article, we will briefly introduce some of the major mathematicians who founded the field.

Before Bayes To better understand Bayesian statistics, we need to go back to the 18th century and refer to the mathematician De Moivre and his treatise The Principle of Chances.[1]

In his dissertation, De Moivre addressed many of the problems of his day related to probability and gambling. As you may know, his solution to one of these problems led to the origin of the normal distribution, but that's another story.

In his thesis, there is a very simple question:

You use a fair coin toss three times in a row to get three positive probabilities.

Reading the problems described in the Rule of Thumb, you may notice that most of these problems start with an assumption and then calculate the probability of a given event from it. For example, in the above problem, there is an assumption that the coin is fair, so the probability of getting a positive in the toss is 0.5.

This is expressed in mathematical terms today as:

𝑃(𝑋|𝜃)

But what if we don't know if this coin is fair?𝜃Is that so?

Thomas Bayes and Richard Price

Almost fifty years later, in 1763, a paper titled The Problems in the Principle of the Potential of Solving Potassium was published in The Potassium Philosophical Exchange of the Royal Society of London.

In the first few pages of the document, there is a text written by mathematician Richard Price summarizing the contents of a paper written by his friend Thomas Bayes a few years before his death. In the introduction, Price explains the importance of some of the discoveries made by Thomas Bayes, which are not included in De Moivre's Principle of Randomness.

In fact, he was referring to a specific issue:

A known number of times an unknown event occurs and fails, finding the probability of its occurrence between any two named probabilities.

In other words, after observing an event, we find an unknown parameter.θWhat is the probability between two probabilities. This is actually one of the first problems in history related to statistical inference, and gave rise to the name inverse probability. In mathematical terms:

𝑃( 𝜃 | 𝑋）

This of course is the posterior distribution we call today Bayes' theorem.

Uncaused Causes

I'm not sure if I'm going to be able to do it.Thomas BayesandRichard Price is a writer.This is actually very interesting. But in order to do this, we need to temporarily put aside some knowledge of statistics.

We are in the 18th century, and probability is becoming an increasingly important area of interest for mathematicians. Mathematicians such as De Moffat or Bernoulli have shown that some events occur with a degree of randomness, but are still governed by fixed rules. For example, if you roll the dice multiple times, one-sixth of the time it stops at six.

Now, imagine that you are a mathematician and a devout believer living in this period. You may be interested to know about this hidden law and its relationship to God.

This is indeed the question that Bayes and Price themselves ask. They want to solve this problem by directly applying the solution to prove that the cosmos must be the result of intelligence and intelligence; thus providing a proof for the existence of God with an ultimate cause, the cause[2] - that is, a cause without a cause.

I'm not sure.

Surprisingly, about two years later, in 1774, apparently without having read the paper by Thomas Bayes, the French mathematician Laplace wrote a paper entitled The Cause of Related Events by the Probability of the Events,[3] a paper on the inverse probability problem. On the first page you can read:

The main principles:

If an event can be caused by n different causes, then the probabilities of these causes of a given event are proportional to each other, and the probability of each of these causes occurring is equal to the probability of the cause of the given event, divided by the sum of the probabilities of each of these causes occurring.

This is what we know today as Bayes' theorem:

​

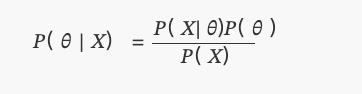
Some of themP(θ)It is a uniform distribution.

The coin experiment

We're going to bring Bayesian statistics to the present using Python and the PyMC library and do a simple experiment.

Suppose a friend gives you a coin and asks if you think it is a fair coin. Because he is in a hurry, he tells you that you can only flip 10 coins. As you can see, there is an unknown parameter in this problem.pAnd we want to estimate this as the probability of getting a positive in the coin toss.pThe most likely value of this is ∞.

(Note: we are not talking about parameters)pThis is a random variable, but the parameter is fixed, and we want to know which values it is most likely to be in between.

In order to have a different view on the issue, we will address it under two different preconceptions:

• 1st, you have no prior knowledge of the fairness of the coin, and you assign equal probabilities topIn this case, we will use the so-called uninformed precedent, because you have not added any information to your beliefs.

• 2 You know from experience that even though the coin may be unfair, it's hard to make it very unfair, so you think of the parameterspIt is unlikely to be less than 0.3 or more than 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ≠ 0.7 ⋅ 0.7 ⋅ 0.7 ⋅ 0.7 ⋅ 0.7 ⋅ 0.7 ⋅ 0.7 ⋅ 0.7 ⋅ 0.7

In both cases, our preconceptions would be:

After tossing the coin 10 times, you get two positive results.p？

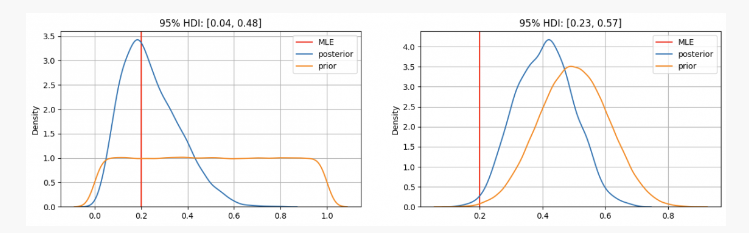
So as you can see, in the first case, we're going to use the parameterspThe prior distribution is concentrated in the maximum likelihood estimate (MLE).p=0.2This is similar to using the frequency-schooling method. The true unknowns will be in the 95% confidence interval, between 0.04 and 0.48.

On the other hand, there's a high degree of confidence that the parameterspIn the case where it should be between 0.3 and 0.7, we can see a posterior distribution of about 0.4, which is much higher than the value given by our MLE. In this case, the true unknowns will be within the 95% confidence interval, between 0.23 and 0.57.

So, in the first case, you would tell your friend that you are confident that the coin is unfair. But in the other case, you would tell him that you are not sure if the coin is fair.

As you can see, even with the same evidence (twice positive out of 10 tosses), the results will be different under different prior beliefs. This is an advantage of Bayesian statistics, similar to the scientific method, which allows us to update our beliefs by combining prior beliefs with new observations and evidence.

END

In today's article, we look at the origins of Bayesian statistics and their major contributors. Since then, there have been many other important contributors to the field of statistics (Jeffreys, Cox, Shannon, etc.).转载自quantdare.com。