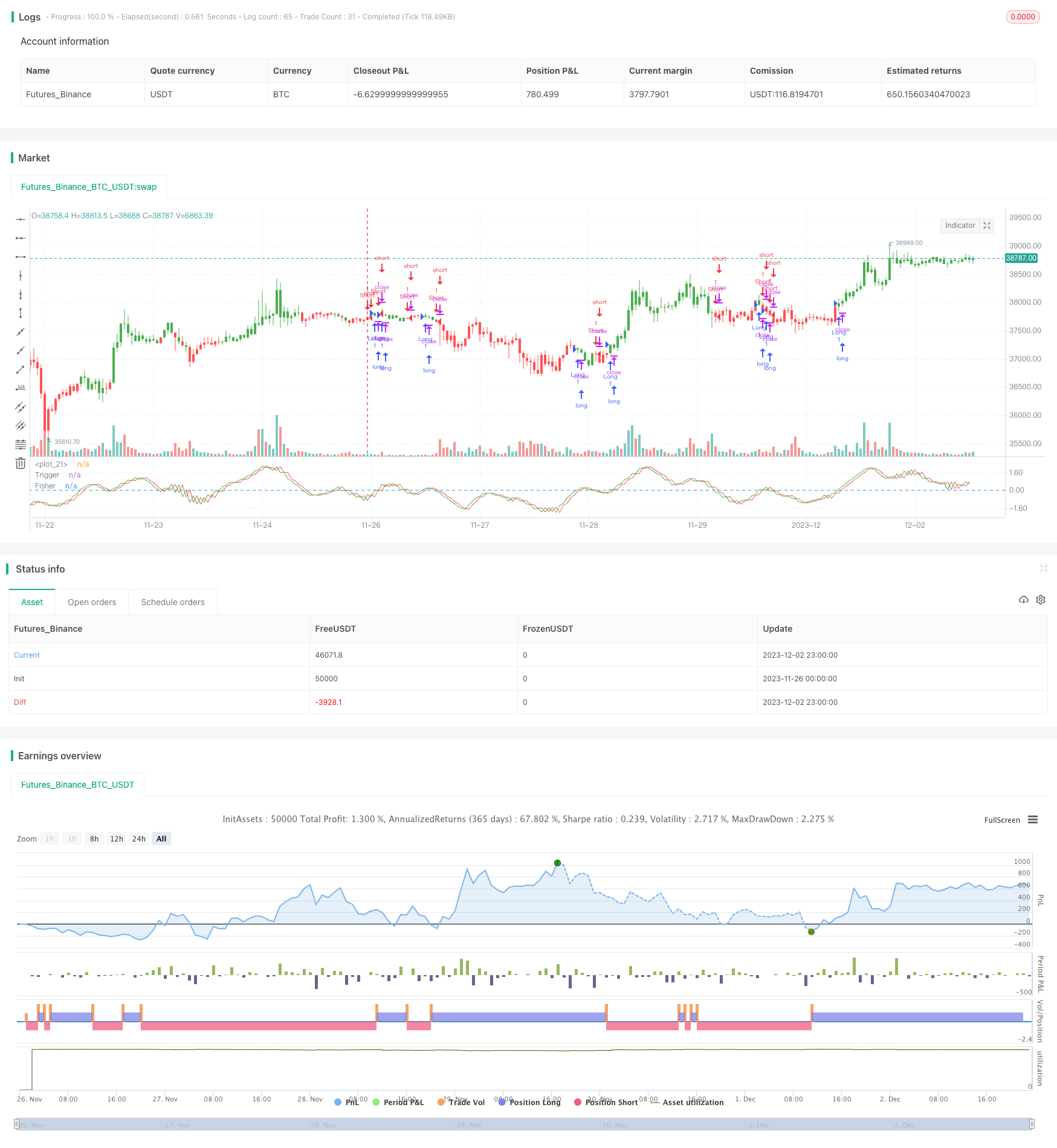
Overview
The Fisher Transform backtest strategy calculates the Fisher transform of prices to identify price reversal points and generate trading signals accordingly. The strategy processes prices using the Fisher transform formula to remove non-Gaussian features of price distributions, resulting in a standardized indicator with an approximate Gaussian distribution. The strategy determines price reversals based on inflection points of the Fisher transform curve and produces long and short signals.
Strategy Principle
The core of this strategy is to process prices using the Fisher transform formula to eliminate non-Gaussian features of natural price distributions. The Fisher transform formula is:
y = 0.5 * ln((1+x)/(1-x))
Here x is the processed price, obtained by first finding the highest and lowest prices over the most recent Length periods using the highest and lowest functions, and then normalizing as follows:
x = (price - minimum)/(maximum - minimum) - 0.5
Prices processed this way approximate a Gaussian distribution. x is then substituted into the Fisher transform formula to obtain the Fisher transform curve. Inflection points in the Fisher transform curve signal price reversals.
When the Fisher transform curve turns from positive to negative, a sell signal is generated. When it turns from negative to positive, a buy signal is generated.
Advantage Analysis
The Fisher transform removes non-Gaussian features from prices, resulting in more well-behaved, standardized prices and fewer false signals
Captures price reversal points, avoiding chasing tops and bottoms
Flexible parameter adjustment for tuning reversal sensitivity
Customizable directionality, adapts to various market environments
Simple logic easy to understand and implement
Risk Analysis
Improper parameter settings may miss turns or generate false signals
Slippage in live trading may prevent perfect signal execution
Hard to identify turns when prices are volatile
Difficult to implement in live trading with need to confirm reversals
Solutions:
Optimize parameters by adjusting Length
Relax entry criteria appropriately to ensure fills
Filter false signals combining other indicators
Strictly follow rules and manage risks
Optimization Directions
Optimize Length parameter to find best combination
Add filters to avoid false signals e.g. moving averages, volatility indicators etc.
Incorporate stop loss to control loss per trade
Add re-entry mechanism to track continuing trends
Conclusion
The Fisher Transform backtest strategy identifies price reversal points by removing non-Gaussian price features. It is an easily implemented mean reversion strategy. Its advantages lie in flexible parameters for catching turns while its main weakness is the difficulty of live implementation with the need for strict entry rules. Various methods can be used to optimize this strategy for practical applicability.
/*backtest
start: 2023-11-26 00:00:00
end: 2023-12-03 00:00:00
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version = 2
////////////////////////////////////////////////////////////
// Copyright by HPotter v2.0 22/12/2016
// Market prices do not have a Gaussian probability density function
// as many traders think. Their probability curve is not bell-shaped.
// But trader can create a nearly Gaussian PDF for prices by normalizing
// them or creating a normalized indicator such as the relative strength
// index and applying the Fisher transform. Such a transformed output
// creates the peak swings as relatively rare events.
// Fisher transform formula is: y = 0.5 * ln ((1+x)/(1-x))
// The sharp turning points of these peak swings clearly and unambiguously
// identify price reversals in a timely manner.
//
// For signal used zero.
// You can change long to short in the Input Settings
// Please, use it only for learning or paper trading. Do not for real trading.
////////////////////////////////////////////////////////////
strategy(title="Fisher Transform Indicator by Ehlers Backtest", shorttitle="Fisher Transform Indicator by Ehlers")
Length = input(10, minval=1)
reverse = input(false, title="Trade reverse")
hline(0, color=blue)
xHL2 = hl2
xMaxH = highest(xHL2, Length)
xMinL = lowest(xHL2,Length)
nValue1 = 0.33 * 2 * ((xHL2 - xMinL) / (xMaxH - xMinL) - 0.5) + 0.67 * nz(nValue1[1])
nValue2 = iff(nValue1 > .99, .999,
iff(nValue1 < -.99, -.999, nValue1))
nFish = 0.5 * log((1 + nValue2) / (1 - nValue2)) + 0.5 * nz(nFish[1])
pos = iff(nFish > 0, 1,
iff(nFish < 0, -1, nz(pos[1], 0)))
possig = iff(reverse and pos == 1, -1,
iff(reverse and pos == -1, 1, pos))
if (possig == 1)
strategy.entry("Long", strategy.long)
if (possig == -1)
strategy.entry("Short", strategy.short)
barcolor(possig == -1 ? red: possig == 1 ? green : blue )
plot(nFish, color=green, title="Fisher")
plot(nz(nFish[1]), color=red, title="Trigger")