Las criptomonedas son una nueva clase de activos y los investigadores están empezando a entender mejor las fuerzas fundamentales detrás de su movimiento de precios. Un nuevo artículo de investigación muestra que el precio de Bitcoin puede modelarse con la ley de Metcalfe.

Resumen de la película:

Demostramos, por ejemplo, que el precio a largo plazo de Bitcoin no es aleatorio, sino que puede modelarse como una función de crecimiento del número de usuarios n con el tiempo. Utilizando los datos observados de Facebook y Bitcoin, derivamos la relación entre el precio, el número de usuarios y el tiempo, y mostramos que el valor de mercado obtenido puede obedecer la función de crecimiento del sigmoide de Gompertz. Esta función se ha utilizado históricamente para describir el crecimiento de organismos biológicos como bacterias, tumores y virus, y puede tener cierta aplicación en la economía de la red.

Citaciones notables en trabajos académicos:

Este artículo ofrece una simple explicación de la formación de precios en el emergente y a menudo mal entendido ecosistema de las criptomonedas. En el caso de Bitcoin, por ejemplo, ofrecemos evidencia empírica convincente de que la formación de precios no es el resultado semirrecurrente de una inversión emocional, sino que se basa en un principio de economía de valor que solo recientemente comenzó a ser reconocido: la economía de la red.

Un examen del precio de Bitcoin ha proporcionado algunas observaciones interesantes que refutan directamente el mito de que el valor de las monedas es un misterio. En primer lugar, como los partidarios han sostenido durante mucho tiempo, el valor de una moneda depende principalmente de su uso y aceptación. Esta hipótesis ha sido comprobada y, a simple vista, la relación entre el precio de Bitcoin y la actividad relacionada con la red de pagos de Bitcoin también es evidente.

La ley de Metcalfe se basa en un término matemático para describir las conexiones entre n usuarios. Por lo tanto, el valor de la red V es una función del número de usuarios n. La base matemática de la ley de Metcalfe se basa en conexiones en pares (por ejemplo, teléfonos). Si cuatro personas en la red usan teléfonos, puede haber un total de 3 + 2 + 1 = 6 conexiones.

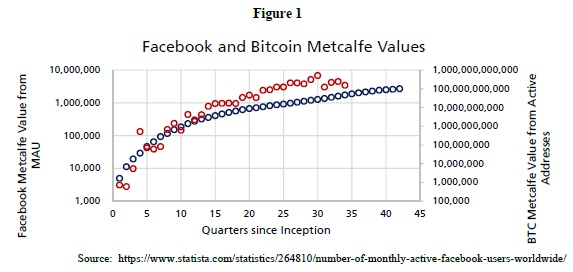
Facebook es muy adecuado para compararlo con Bitcoin. Cada serie de datos tiene casi la misma longitud (aproximadamente 10 años). Ambos son bastante innovadores, aunque no completamente originales (Digicash antes que Bitcoin, MySpace antes que Facebook). Raramente hay una oportunidad de ver una moneda u otro activo que se adopte gradualmente con el tiempo.

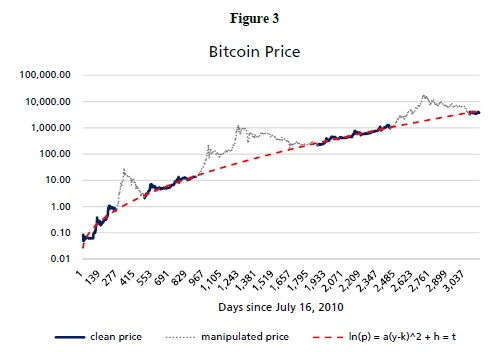
Reflexionando en la Figura 3, hay tres excepciones notables, la tendencia de desviación de la parálisis del precio de Bitcoin. Estos son períodos de manipulación de precios registrados y de equilibrio final. Estos picos representan desviaciones de precios que no pueden ser explicadas por factores relacionados con el usuario.

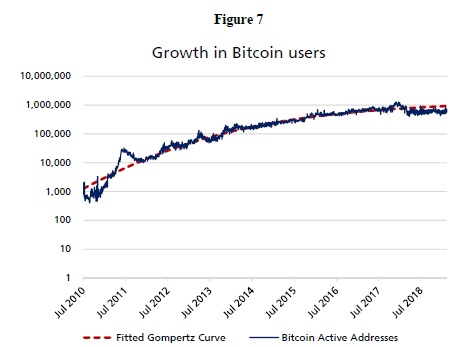
Si n crece a una tasa constante, entonces log (n) es lineal. Como observamos que log (n) es no lineal tanto en Facebook como en Bitcoin (Fig. 7), por lo tanto, n crece a una velocidad no constante, lo que indica que la adopción está en diferentes etapas. Este modelo de tasa de crecimiento acumulado ha dado lugar a la función en forma de S (función Gompertz) que ha sido utilizada durante décadas para simular infecciones virales, crecimiento bacteriano, crecimiento tumoral y popularidad de los teléfonos móviles.[2018], con el que simula el coeficiente de parentesco de Metcalfe. Utilizando datos diarios de n cuentas activas de agentes, aplicamos esta ecuación a la dirección activa de la figura 7.

En la actualidad, el bitcoin es el principal activo de las criptomonedas.