Hablemos de cómo optimizar los parámetros de varios modelos de transacción programatizados.

Hablemos de cómo optimizar los parámetros de varios modelos de transacción programatizados.

• Parámetros de las tierras altas y de las islas

Un principio importante en la optimización de parámetros es buscar plazas de parámetros en lugar de aislamientos de parámetros. La llamada playa de parámetros se refiere a la existencia de un rango de parámetros más amplio, en el que el modelo puede obtener mejores resultados, generalmente con el centro de la planicie formando una distribución aproximada. La llamada isla de parámetros se refiere a que el modelo se desempeña mejor solo cuando el valor de los parámetros está dentro de un rango muy pequeño, y cuando los parámetros se desvían de este valor, la expresión del modelo varía significativamente.

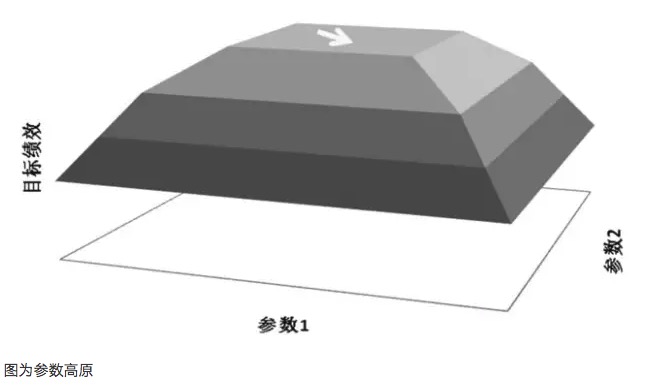
• Gráfico de los parámetros de la meseta

  Por ejemplo, si un modelo de negociación tiene dos parámetros, los parámetros 1 y 2, se obtiene una imagen tridimensional de los resultados cuando se prueban los dos parámetros. Una buena distribución de parámetros debe ser la imagen de los parámetros, incluso cuando la configuración de los parámetros se desvía, el rendimiento de la ganancia del modelo puede ser garantizado.

  

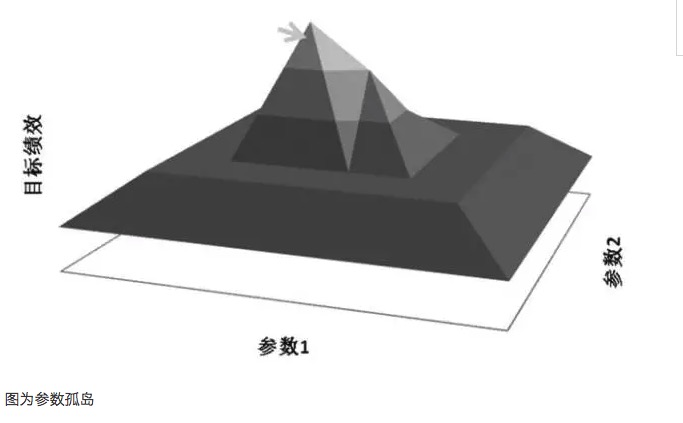
  En general, si el rendimiento de un sistema de parámetros cercanos difiere mucho del rendimiento del parámetro óptimo, entonces este parámetro óptimo puede ser un resultado de una suma excesiva, que puede considerarse matemáticamente como una solución singular, no como una solución de valores extremos. Desde un punto de vista matemático, las singularidades son inestables y, en situaciones de incertidumbre futuras, una vez que las características del mercado cambian, el parámetro óptimo puede convertirse en el parámetro peor.

  El exceso de adecuación se relaciona con la muestra seleccionada, si la muestra seleccionada no puede representar las características generales del mercado, sino que solo se ajusta los parámetros para que el resultado de la prueba alcance los valores esperados positivos. Esta práctica es indudablemente un autoengaño, y el valor de los parámetros obtenido es el valor de los parámetros no válidos del exceso de adecuación. Por ejemplo, al analizar el exceso de adecuación de los parámetros, el modelo de negociación presenta un fenómeno de aumento repentino de los rendimientos en los valores 35 y 63 respectivamente.

  La principal contradicción entre el exceso de adecuación y la optimización de parámetros es que los parámetros óptimos obtenidos por la optimización de parámetros de modelos se basan solo en una muestra de datos históricos que ya han ocurrido, mientras que el mercado futuro es un cambio dinámico, con similitudes y variaciones en comparación con el mercado histórico. Los diseñadores de modelos pueden encontrar los parámetros con los que el modelo se desempeña mejor en la historia, pero este parámetro no es necesariamente el mejor en la aplicación real del modelo futuro, sino el parámetro con el mejor desempeño histórico del modelo, que puede funcionar muy mal en la futura guerra de modelos, incluso con un gran daño.

  Además, los platos de parámetros y los islotes de parámetros a menudo tienen una relación más grande con el número de transacciones. Si el número de transacciones del modelo es menor, a menudo se puede encontrar un punto de parámetros adecuado para que el modelo sea rentable en todas estas transacciones, y la ganancia del modelo optimizado con este parámetro refleja una mayor casualidad. Si el número de transacciones del modelo es mayor, la casualidad de la ganancia del modelo disminuye, y refleja más la inevitabilidad y regularidad de la ganancia, también hay un platón de parámetros.

• Cómo optimizar los parámetros

  Una vez que se entiende el plano de parámetros y el aislamiento de parámetros, resulta importante el método de optimización de los parámetros, especialmente cuando hay varios parámetros en el modelo (en lo sucesivo denominados conjuntos de parámetros), a menudo la toma de valor de un parámetro afecta a la distribución del plano de parámetros de otro. ¿Cómo se optimiza el conjunto de parámetros?

  Un método es la convergencia progresiva; es decir, primero se optimiza por separado un parámetro y se fija después de obtener su valor óptimo, y luego se optimiza otro parámetro para obtener su valor óptimo y se fija. Así, el ciclo continúa hasta que los resultados de la optimización no cambian. Por ejemplo, un modelo de negociación de compra y venta cruzada uniforme, con dos parámetros independientes, respectivamente, el ciclo corto N1 y el ciclo largo N2. Primero se fija N2 a 1, se selecciona la prueba de N1 en un rango de valores de 1 a 100, se busca el valor óptimo y se obtiene el valor óptimo 8 y se fija; se optimiza N2 entre 1200 y se obtiene el valor óptimo 26 y se fija; se vuelve a optimizar la segunda ronda para N1 y se obtiene un nuevo valor óptimo 10 y se fija; finalmente se optimiza N2 y se fija el valor 28.

  Otro método es utilizar una plataforma de diseño de software programático con capacidades de cálculo más potentes para calcular directamente la distribución entre la función objetivo y el conjunto de parámetros, y luego buscar la distribución de diferencias multidimensionales, definiendo un umbral de diferenciación, cuyo valor absoluto de diferenciación es menor que el máximo de volumen multidimensional correspondiente en el rango del umbral, el más alto del radio de esfera multidimensional, elegido como el parámetro de toma de valor más estable.

  Además de los métodos de optimización de parámetros, la selección de la muestra de datos también es un factor importante. Los modelos que siguen tendencias como idea de negociación funcionan mejor cuando surgen mercados tendenciales, y las estrategias de compra alta y baja como idea de negociación funcionan mejor en mercados oscilantes. Por lo tanto, cuando se optimiza los parámetros, es necesario eliminar adecuadamente los mercados que coinciden con la idea de negociación para considerar la ganancia e incrementar los datos de los mercados que no aceptan la idea de negociación para considerar la pérdida.

  Tomando como ejemplo los futuros de los índices de valores, desde el inicio de la cotización en 2010 y desde la segunda mitad de 2014, cuando surgió el mercado de los extremos de los toros, los futuros de los índices de valores son unilaterales. No hay duda de que todos los modelos de tendencia obtienen buenos resultados. Sin embargo, si también introducimos datos de estos mercados extremos en la muestra para optimizar los parámetros, los parámetros del modelo obtenidos no son necesariamente los mejores.

  Por ejemplo, supongamos que un modelo tiene dos parámetros, los resultados de las pruebas del Parámetro A son muy buenos en el momento del mercado unilateral y son generales en otros momentos; los resultados de las pruebas del Parámetro B son peores en el momento del mercado unilateral y son mejores en otros momentos, y la distribución entre los parámetros A es más uniforme. Incluso si el Parámetro A es superior al Parámetro B en los indicadores integrales de las pruebas de datos de la muestra, como el riesgo y el rendimiento, preferimos el Parámetro B, ya que el Parámetro B es relativamente más estable y no depende de la muestra específica.

  En resumen, cuando se construye un modelo de negociación programática, por un lado, se puede optimizar el modelo de mejora mediante parámetros para que el modelo se adapte mejor a los patrones de fluctuación de precios y mejore la rentabilidad de la inversión; por otro lado, se debe evitar una adaptación excesiva a la optimización de parámetros, lo que reduce significativamente la adaptabilidad del modelo a los cambios en el mercado.

Transcrito por el comerciante programado