Fórmula de Kelly: una herramienta poderosa para el control de posiciones

**Supongamos que la probabilidad de ganar es del 60% y la probabilidad de perder es del 40%. La tasa de ganancia neta es del 100% y la tasa de pérdida es del 100%. Es decir, si gana, puede ganar un dólar por cada dólar que ponga, y si pierde, perderá un dólar por cada dólar que ponga.

• 1. Para esta apuesta, el beneficio esperado por cada apuesta es del 60% de la cantidad apostada.*1-40%*1 = 20%, la expectativa de ganancia es positiva. Es decir, es una situación en la que los piratas tienen una ventaja, y una gran ventaja.

Entonces, ¿cómo apostaríamos?

Si no pensamos con rigor, imaginemos que, dado que mi expectativa de ganancia en cada apuesta es del 20%, para lograr el máximo beneficio a largo plazo, debería intentar poner en cada apuesta una mayor proporción del capital. El máximo valor de esta proporción es del 100%.

Pero es obvio que cada juego de apuestas en el 100% del capital no es razonable, ya que una vez que el juego de apuestas de perder, entonces todo el capital se perderá, no podrá participar en la siguiente ronda, sólo puede salir tranquilamente. Y en el largo plazo, el juego de perder una vez que este evento es inevitable, por lo que en el largo plazo es la quiebra.

Así que la conclusión es que si existe la posibilidad de que un empate pierda todo el capital de una vez, aunque sea muy pequeña, nunca se puede llenar la posición. Porque en el largo plazo, los eventos de pequeña probabilidad son inevitables, y en la vida real, la probabilidad real de que ocurran eventos de pequeña probabilidad es mucho mayor que su probabilidad teórica. Este es el efecto cola de aceite en la economía.

• 2 Continuamos con el punto muerto 1 ◦ Si cada apuesta del 100% es irracional, ¿qué pasa con el 99%? Si cada apuesta del 99% no solo garantiza que nunca se vaya a la quiebra, sino que con buena suerte puede generar grandes ganancias.

¿Es esto lo que sucede en la realidad?

En vez de analizar el problema teóricamente, podemos hacer un experimento. Simulamos el empate y apostamos el 99% cada vez para ver qué pasa.

Este simulacro es muy sencillo y se puede hacer con Excel.

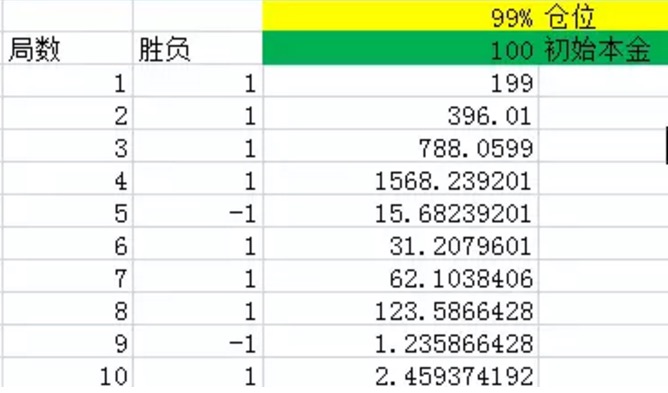Figura 1 y 2

La primera columna indica el número de tiradas. La segunda columna indica el número de tiradas ganadas y perdidas. Excel produce 1 con una probabilidad de 60%, es decir, una probabilidad de 60% de ganancias netas. La tercera columna indica el número de tiradas ganadas y perdidas.

Como se puede ver en el gráfico, después de 10 juegos, el número de juegos ganados en 10 juegos es de 8, con una probabilidad mayor del 60%, solo perdió dos veces. Pero incluso así, el último dinero que quedó fue de 2.46 yuanes, lo que es básicamente una pérdida de luz.

Cuando aumentamos el número de experimentos a 1000, 2000 y 3000… el resultado es que, al final, el dinero en mano es básicamente hacia cero.

Si el 99% no funciona, entonces vamos a intentarlo con otras proporciones, como se muestra a continuación: En el gráfico se puede ver que cuando la posición se reduce gradualmente, de 99%, a 90%, 80%, 70%, 60%, el resultado de las mismas 10 juegos es completamente diferente. En el gráfico parece que se puede ver que a medida que la posición se reduce gradualmente, el dinero después de las 10 juegos es gradualmente más grande.

Si miramos aquí, veremos que el problema del empate no es tan sencillo. Incluso si los jugadores ganan en un empate tan grande, no se puede ganar dinero de forma casual.

Entonces, ¿cómo apostar para obtener el máximo beneficio a largo plazo?

¿Es que, como se muestra en el diagrama de arriba, cuanto menor sea la proporción, mejor?

Entonces, ¿cuál es la proporción óptima?

¡Ese es el problema que tiene que resolver la famosa fórmula de Kelly!

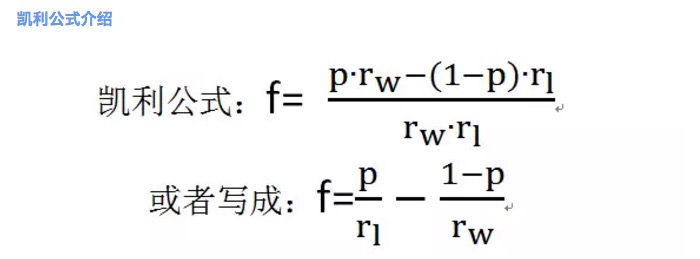Se muestra en la Figura 2.

Donde f es la proporción de apuesta óptima; p es la probabilidad de ganar; rw es la tasa de ganancia neta cuando se gana, por ejemplo, en la apuesta 1, rw = 1; rl es la tasa de pérdida neta cuando se pierde, por ejemplo, en la apuesta 1, rl = 1; tenga en cuenta que rl> 0;

De acuerdo con la fórmula de Kelly, se puede calcular que el porcentaje de apuestas más alto en el empate 1 es del 20%.

Podemos hacer un experimento para entender mejor esta conclusión.

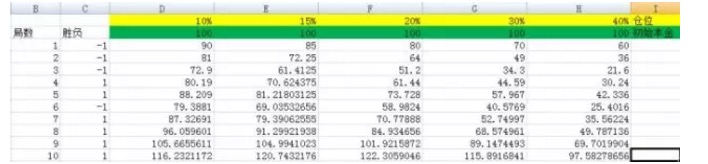Figura 3 y 4

En la imagen, hemos establecido posiciones de 10%, 15%, 20%, 30% y 40% respectivamente. Sus columnas correspondientes son D, E, F, G y H respectivamente.

Y cuando lo hice 3000 veces, Y cuando lo hice 5000 veces, Se puede ver que la columna F corresponde al resultado más grande, y la raíz de presión en relación con las otras columnas no es una escala cuantitativa. Y la columna F corresponde a la proporción de posiciones del 20% .

En el experimento anterior, si tienes la mala suerte de elegir el 40% de la proporción, es decir, la columna H correspondiente, después de apostar 5.000 juegos, tu capital se convertirá de 100 a 22799985.75, con un gran beneficio. Pero en comparación con el resultado del 20% de la proporción, eso es lo mismo que no ganar dinero.

¡Ese es el poder del conocimiento!

• 3 Comprendimiento de la fórmula de Kelly

La inferencia matemática de la fórmula de Kelly y su complejidad requieren un conocimiento matemático muy profundo, por lo que no tiene mucho sentido discutirla aquí. Aquí profundizaré en la comprensión subjetiva de la fórmula de Kelly a través de algunos experimentos.

Veamos otra apuesta. apuesta 2: la probabilidad de que pierda y gane es del 50%, por ejemplo, el lanzamiento de la moneda. Cuando gana, la tasa de ganancia neta es de 1, es decir, rw = 1, cuando pierde, la tasa de pérdida neta es de 0.5, es decir, rl = 0.5.

Es fácil ver que la ganancia esperada para el empate 2 es de 0.25, otro empate en el que los jugadores tienen una gran ventaja.

De acuerdo con la fórmula de Kelly, podemos obtener el mejor porcentaje de apuestas por juego:

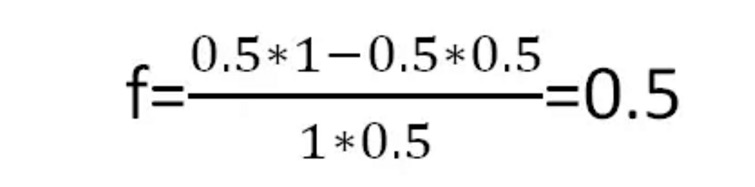Se muestra en la figura 4.

En otras palabras, cada vez que apuestas la mitad de tu dinero, obtendrás el mayor beneficio a largo plazo.

A continuación, voy a dar un concepto de la tasa de crecimiento promedio r basado en la experimentación.

En primer lugar, veamos el experimento 2.1, los dos gráficos siguientes:

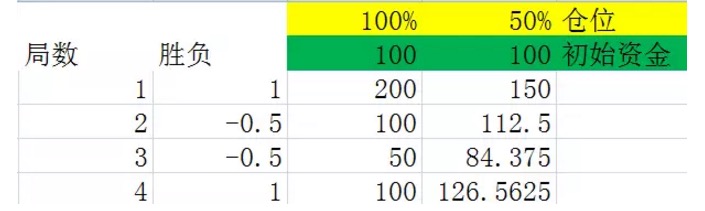Se muestra en la figura 5.

Estos dos gráficos son experimentos realizados para simular la parálisis 2, en la segunda columna de la columna negativa, la probabilidad de que el experimento se produzca es del 50%, lo que significa que el beneficio es del 100%. La probabilidad del 50% es del -0.5, lo que significa que la pérdida es del 50%. La tercera y cuarta columnas son los fondos que se poseen después de cada parálisis con posiciones del 100% y 50%, respectivamente.

Si se comparan cuidadosamente los dos gráficos, se puede llegar a la conclusión de que, después de pasar el mismo número de tiros, el resultado final solo está relacionado con el número de tiros ganados y el número de tiros perdidos en estos números de tiros, y no con el orden de las tiras ganadas y perdidas en estos números de tiros. Por ejemplo, en los dos gráficos anteriores, también se realizaron 4 tiros, y también en cada uno de los gráficos se ganaron dos tiros perdidos, pero el orden de pérdidas en el primer gráfico fue ganado y perdido, y el orden de pérdidas en el segundo gráfico fue ganado y perdido.

Por supuesto, esta conclusión es muy fácil de demostrar (la ley de intercambio de la multiplicación, los niños de primaria lo harán), pero aquí no se demuestra, los dos ejemplos mencionados anteriormente son suficientes para que todos los entendamos bien.

Entonces, dado que el resultado final no tiene nada que ver con el orden de ganancias y pérdidas, supongamos que el empate 2 se realice como en el experimento 2.2, como se ve en la siguiente imagen:

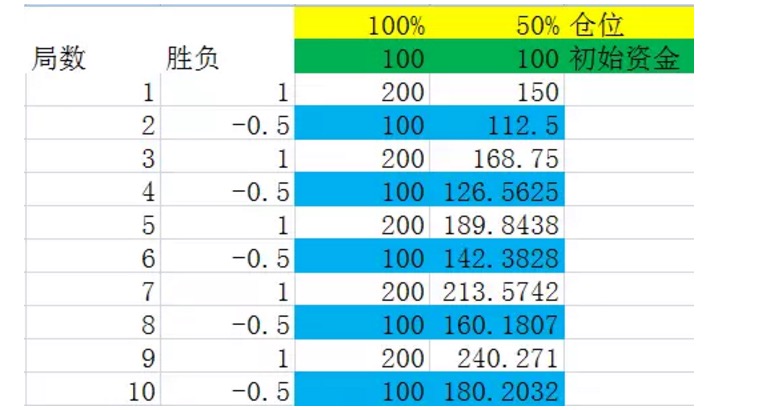Se muestra en la Figura 6.

Suponemos que el empate se gana y se gana de forma alternada, ya que concluimos que a largo plazo esto no tiene ningún impacto en el resultado financiero.

Antes de observar la imagen, hacemos una definición. Supongamos que consideramos un conjunto de paradas como un conjunto en el que la frecuencia de los resultados es exactamente igual a su probabilidad, y el número de paradas de este conjunto es el número medio más pequeño de todos los conjuntos que cumplen las condiciones, entonces llamamos a este conjunto un conjunto de paradas. Por ejemplo, en el experimento de la imagen anterior, un conjunto de paradas representa una parada de dos paradas, en la que se gana una vez y se pierde una vez.

Observe con atención los números marcados en azul en el gráfico anterior, que son el final de una serie de paradas. Encontrará que estos números se mantienen en un crecimiento constante. Cuando la posición es del 100%, el crecimiento de los números marcados en azul es del 0%, es decir, el crecimiento del capital después de una serie de paradas es del 0%. Esto también explica que cuando cada vez que se llena la posición, no se puede ganar dinero a largo plazo en la serie de paradas 2. Cuando la posición es del 50% (es decir, la mejor proporción obtenida por la fórmula de Kelly), el crecimiento de los números marcados en azul es del 12.5%, es decir, el crecimiento del capital después de una serie de paradas es del 12.5%

Es una ley general que la tasa de crecimiento después de cada grupo estancado está relacionada con la posición. Y cuanto mayor sea la tasa de crecimiento después de cada grupo estancado, mayor será el beneficio final a largo plazo.

De acuerdo con la tasa de crecimiento de cada grupo de paradojas se puede calcular la tasa de crecimiento promedio de cada paradoja g. En el gráfico de arriba, si cada grupo de paradojas contiene dos paradojas, entonces la tasa de crecimiento promedio de cada paradoja

Figura 7 Se muestra

En el largo plazo, para obtener el mayor crecimiento de capital, se debe maximizar r, es decir, maximizar g. La mejor proporción de apuesta f se obtiene resolviendo max (g).

• 4 Otras conclusiones de la fórmula de Kelly sobre el riesgo

La leyenda de Kelly

La fórmula de Kelly fue originalmente desarrollada para John Larry Kelly, físico de AT&T Bell Laboratories, basándose en la investigación de su colega Claude Elwood Shannon sobre el espionaje de líneas telefónicas de larga distancia. Kelly resolvió el problema de cómo aplicar la teoría de la información de Shannon a un jugador que posee información interna en un juego de azar. El jugador desea decidir la mejor cantidad de apuesta, y su información interna no necesita ser perfecta (sin espionaje), lo que le permite tener una ventaja útil. Thorpe aprovechó el tiempo que le quedaba de su trabajo para escribir, a través de meses de arduos cálculos, un ensayo matemático titulado “La estrategia preferida de las apuestas de las apuestas de 21 puntos”. Utilizó su conocimiento para hacer una incursión nocturna en todos los casinos de la ciudad de Reno, Nevada, y ganó con éxito decenas de miles de dólares en las mesas de apuestas de 21 puntos. También fue el antepasado del fondo de cobertura de comercio cuantitativo de Wall Street en los Estados Unidos, creando el primer fondo de cobertura de comercio cuantitativo en los años 70.

El uso de la perspectiva

¿Cómo usar la fórmula de Kelly para ganar dinero en la vida real? En mi opinión, la paradoja debe provenir de los mercados financieros. Hace poco estuve haciendo un estudio de los sistemas de negociación, ¿qué es lo más importante para un buen sistema de negociación? Una regla de compra y venta con expectativas positivas de ganancias es el 10% de la importancia, mientras que un buen método de control de fondos es el 40% de la importancia, y el 50% restante es el control mental de la gente. Y la fórmula de Kelly es la herramienta que me ayuda a controlar mis posiciones financieras. Por ejemplo, un sistema de negociación de acciones que he estudiado anteriormente, que realiza una operación por semana, la probabilidad de éxito de la operación es de 0.8, la probabilidad de fracaso es de 0.2. Cuando el éxito se puede ganar el 3% (deduciendo la comisión, el impuesto sobre el valor agregado), el 5% de la pérdida de cada fracaso. Antes de saber la fórmula de Kelly, yo estaba ciegamente lleno de posición de negociación, y no sabía que mi posición se estableció incorrectamente, la mente es muy virtual. Después de usar la fórmula de Kelly, la posición óptima calculada debe ser 9.33, es decir, si el interés de préstamo es de 0, si se quiere obtener la mayor velocidad de crecimiento de capital, se debe utilizar el comercio de apalancamiento, mediante el cálculo de la fórmula obtenido por cada operación de crecimiento de capital promedio r es de aproximadamente el 7,44%, mientras que el comercio de la posición llena de la tasa de crecimiento de capital promedio es de aproximadamente r 1.35 (es decir, la rentabilidad esperada). Por supuesto, la fórmula de Kelly no puede ser tan simple en su aplicación práctica, y hay muchas dificultades que deben ser superadas. Por ejemplo, el costo de los fondos requeridos por las bolsas de palanca, por ejemplo, el dinero en la realidad no es infinitamente distribuible, por ejemplo, en los mercados financieros no es tan simple como la simple parálisis mencionada anteriormente. Pero de todos modos, la fórmula de Kelly nos muestra el camino a seguir.