Pronóstico del precio de Bitcoin en tiempo real con el marco LSTM

Nota: Este caso es solo para uso de investigación y no constituye una recomendación de inversión.

Los datos del precio de Bitcoin se basan en la secuencia de tiempo, por lo que la predicción del precio de Bitcoin se realiza principalmente con el modelo LSTM.

La memoria a corto plazo (LSTM) es un modelo de aprendizaje profundo que se aplica especialmente a datos de secuencia de tiempo (o datos con orden de tiempo / espacio / estructura, como películas, oraciones, etc.) y es el modelo ideal para predecir la dirección del precio de las criptomonedas.

Este artículo se centra en la combinación de datos a través del LSTM para predecir el precio futuro de Bitcoin.

Importar librerías para usar

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Análisis de datos

Carga de datos

Leer los datos diarios de BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

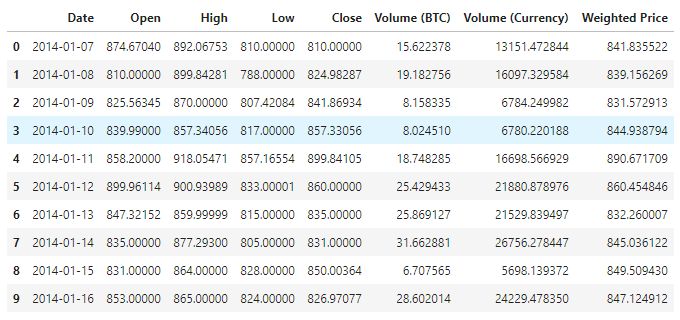
Para ver los datos disponibles, ahora hay un total de 1380 artículos de datos, los cuales se componen de las columnas Date, Open, High, Low, Close, Volume (BTC), Volume (Currency) y Weighted Price. Excepto la columna Date, el resto de columnas son de tipo float64.

data.info()

Vea los datos de las 10 primeras líneas.

data.head(10)

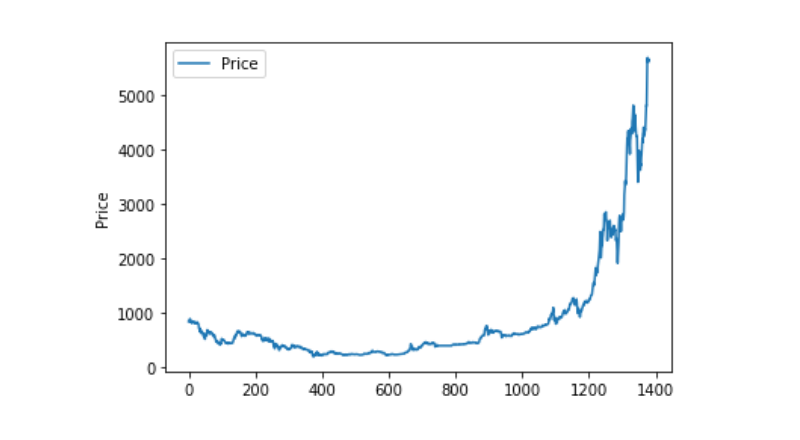
Visualización de datos

Utilizamos matplotlib para trazar el precio ponderado y ver la distribución y el movimiento de los datos. En el gráfico encontramos una parte de los datos 0 y necesitamos confirmar si hay alguna anomalía.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Procesamiento de datos excepcional

Primero vamos a ver si hay datos de nan, y podemos ver que no hay datos de nan en nuestros datos.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Si miramos el dato de 0 de nuevo, podemos ver que nuestro dato contiene un valor de 0, y tenemos que procesar el valor de 0.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

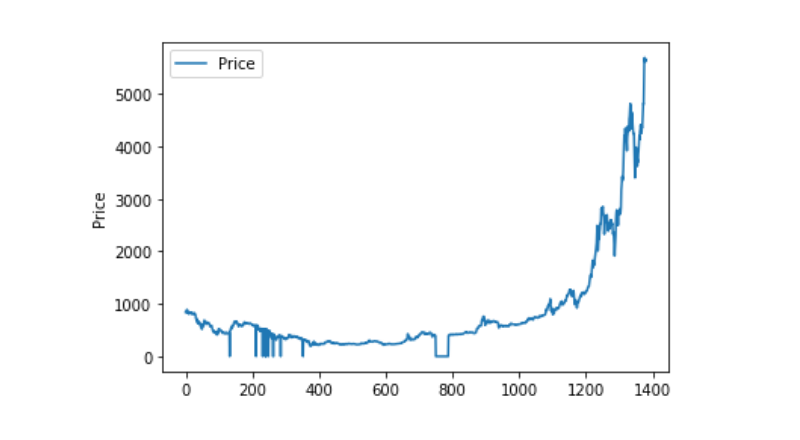
Y si vemos la distribución y el movimiento de los datos, entonces la curva es muy continua.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

División de los conjuntos de datos de entrenamiento y de prueba

Para agrupar los datos en 0 a 1.

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Se divide el conjunto de datos de prueba y el conjunto de datos de entrenamiento en 2:8.

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Crear conjuntos de datos de entrenamiento y prueba, con un día como ventana para crear nuestros conjuntos de datos de entrenamiento y prueba.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Definir y entrenar modelos

Esta vez usamos un modelo sencillo que tiene la estructura de 1. LSTM2. Dense.

Aquí se necesita explicar la forma de entrada de LSTM. La dimensión de entrada de Input Shape es "batch_size, time steps, features"; donde, el valor de los pasos de tiempo es el intervalo de la ventana de tiempo en el momento de la entrada de datos, donde usamos 1 día como ventana de tiempo, y nuestros datos son datos de día, por lo que aquí nuestros pasos de tiempo son 1.

La memoria a corto plazo (LSTM) es un tipo de RNN especial que se utiliza principalmente para resolver la desaparición de gradientes y la explosión de gradientes durante el entrenamiento de secuencias largas.

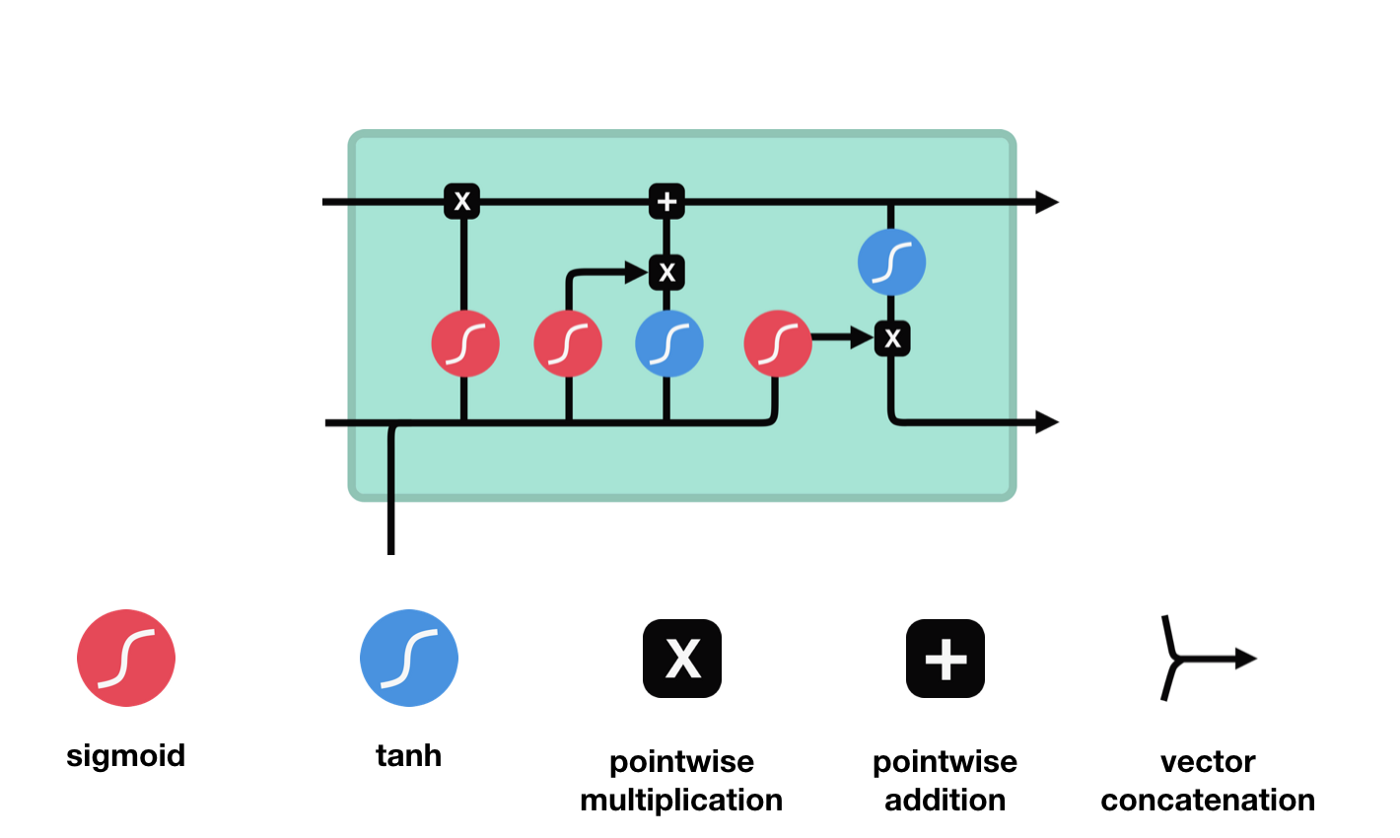
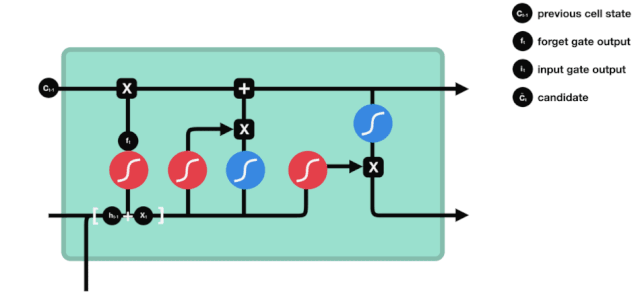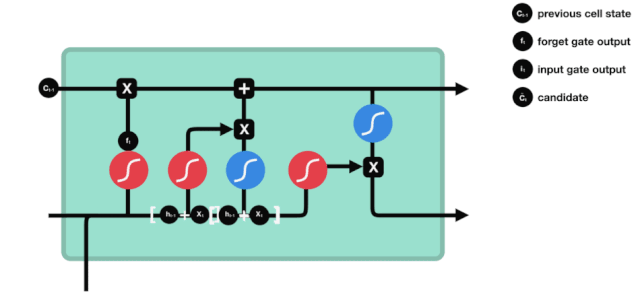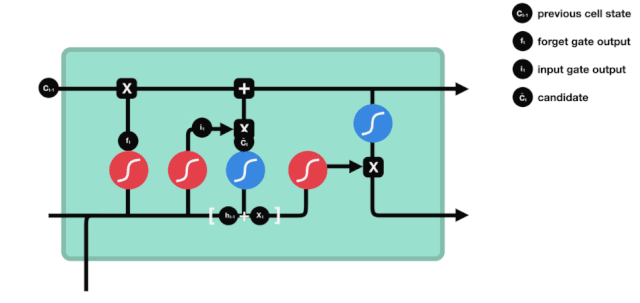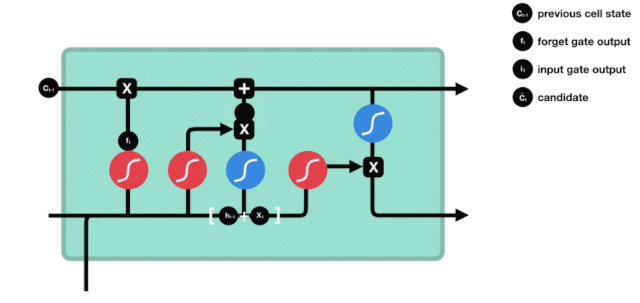
Desde el diagrama de la estructura de red de LSTM, se puede ver que LSTM es en realidad un modelo pequeño, que contiene 3 funciones de activación sigmoides, 2 funciones de activación tanh, 3 multiplicaciones y una suma.

Estado de las células

El estado celular es el núcleo del LSTM, es la línea negra en la parte superior del gráfico, y debajo de esta línea negra hay algunas puertas, que se presentan más adelante. El estado celular se actualiza según los resultados de cada puerta.

Las redes LSTM pueden eliminar o agregar información sobre el estado de las células a través de una estructura llamada puerta. Las puertas pueden decidir selectivamente qué información debe pasar. La estructura de las puertas es una combinación de una capa sigmoide y una operación multiplicada por un punto.

Las puertas olvidadas

El primer paso del LSTM es decidir qué información debe ser eliminada por el estado celular. Esta parte de la operación es procesada por una unidad sigmoide llamada puerta del olvido.

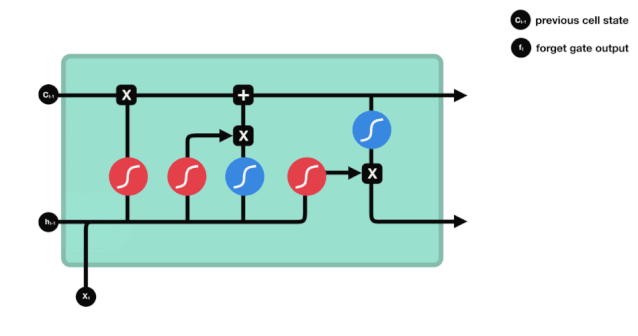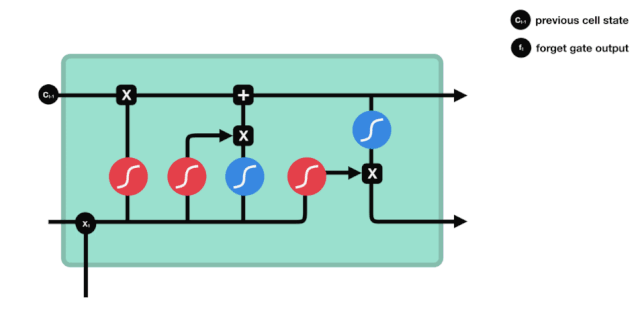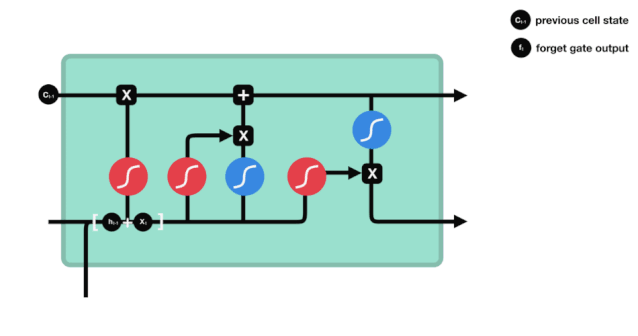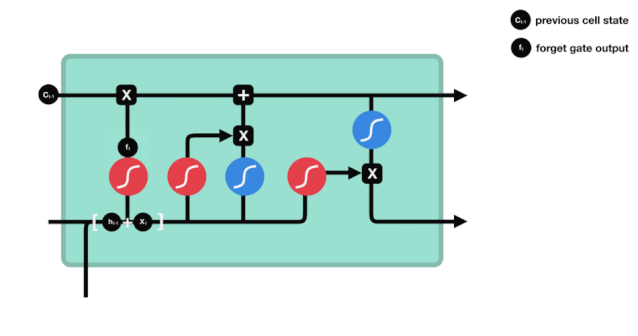
Se puede ver que la puerta del olvido produce un vector entre 0 y 1 al ver la información $h_{l-1}$ y $x_{t}$, donde el valor de 0 a 1 indica qué información se retiene o se descarta en el estado celular $C_{t-1}$. 0 indica que no se retiene y 1 indica que se retiene.

Expresión matemática: $f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

La entrada

El siguiente paso es decidir qué nueva información se añade al estado de la célula, y esto se hace mediante la entrada de la puerta.

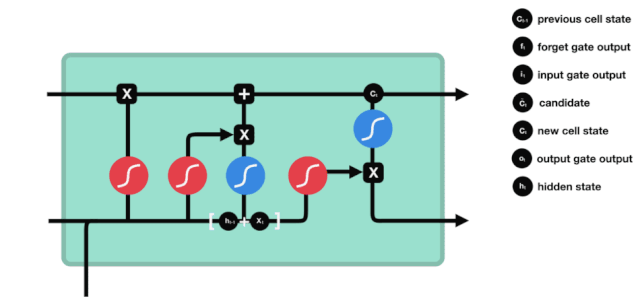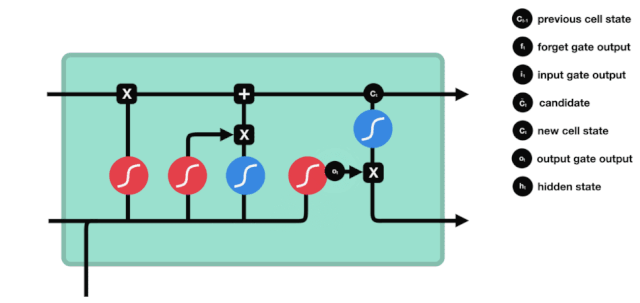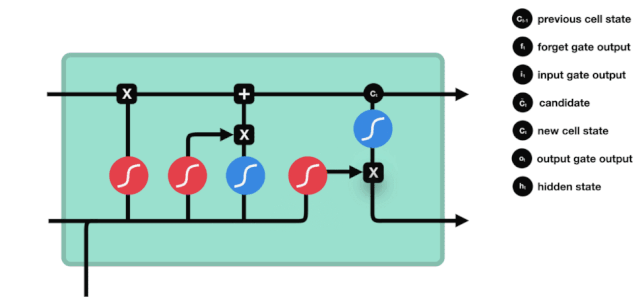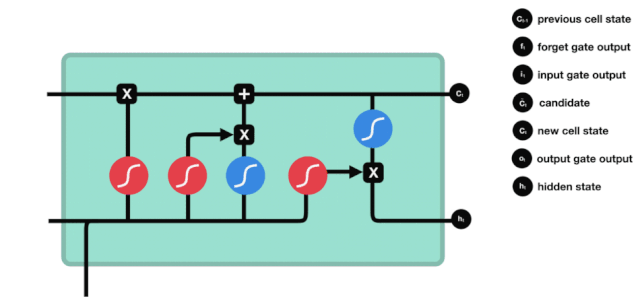
Vemos que la información de $h_{l-1}$ y $x_{t}$ se vuelve a poner en una puerta de olvido (sigmoid) y en la entrada (tanh). Como la salida de la puerta de olvido es de 0-1, por lo tanto, si la salida de la puerta de olvido es 0, el resultado después de la entrada $C_{i}$ no se agregará al estado actual de la célula, si es 1, todo se agregará al estado de la célula, por lo que el papel de la puerta de olvido aquí es agregar selectivamente el resultado de la entrada al estado de la célula.

La fórmula matemática es $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t} $

Puerta de salida

Después de actualizar el estado de la célula, se necesita determinar qué características de estado de la célula de salida se determinan en función de las sumas de $h_{l-1}$ y $x_{t}$ ingresadas. Aquí se necesita determinar las condiciones de la entrada a través de una capa sigmoide llamada puerta de salida, y luego determinar el estado de la célula a través de la capa tanh para obtener un vector con un valor entre -1 ~ 1, que se multiplica por las condiciones de decisión obtenidas por la puerta de salida para obtener la salida final de la unidad RNA, como se muestra en el diagrama de animación.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

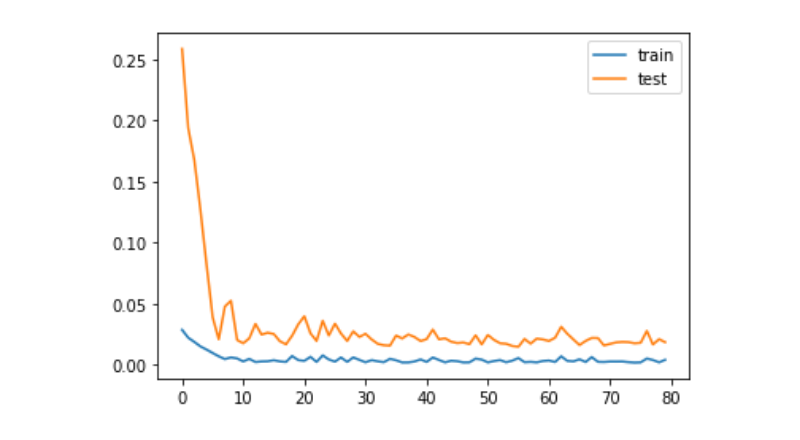
history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Pronóstico

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

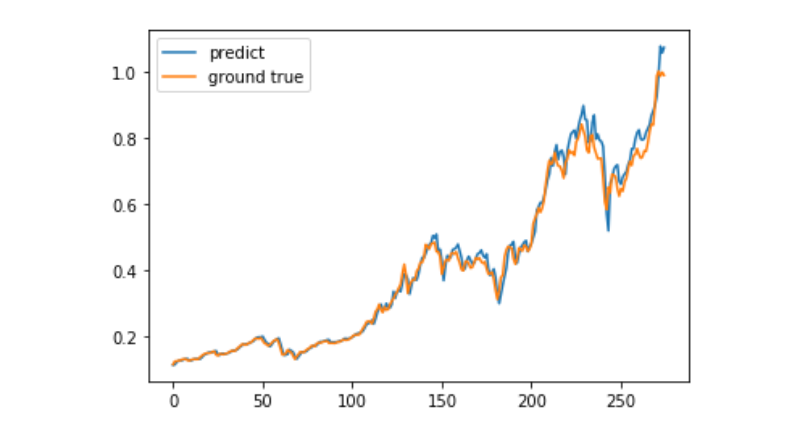
En la actualidad, es muy difícil predecir el movimiento del precio de Bitcoin a largo plazo con el aprendizaje automático, y este artículo solo puede ser utilizado como un caso de aprendizaje. El caso luego se lanzará en línea con una nube de matriz en una imagen demo que los usuarios interesados pueden experimentar directamente.