La curva de los dioses y el monstruo

En la edición anterior se decía que Jacob Bernoulli había fallecido sin haber publicado su libro de conjeturas sobre la teoría de la probabilidad. La tarea de ordenar su manuscrito fue confiada a su sobrino, Nicolás II Bernoulli (el genio de la madrugada). El nombre de Abraham de Moivre se traduce en muchos lugares como “Moivre”, aunque después de ver su retrato, no estoy muy de acuerdo con la traducción posterior. Esta invitación podría haber logrado un período de glorificación en la vida futura, pero Moivre lo rechazó. Y la razón por la que lo rechazó fue que sentía que no tenía la suficiente fuerza de inundación.

• ¿Cómo se llama? Más tarde, el rey de Francia, Luis XIV, promulgó un decreto que declaraba a los protestantes nacionales ciudadanos inferiores y que los niños debían convertirse al protestantismo, lo que esencialmente convirtió al protestantismo en una secta en Francia, por lo que Montmorency pasó dos años en prisión. Montmorency intentó huir de la cárcel a Inglaterra, pero nunca obtuvo un puesto académico, a pesar de su amistad con Newton y de ser miembro de la familia real británica a los 30 años. Montmorency dependía de otros matemáticos y mentores para ganarse la vida, y el hecho de que sus matemáticas básicas fueran una carga para el día a día, y que sus juegos y insultos fueran el resultado de su vida en Francia, lo que le llevó a la ceguera hasta los 87 años, cuando fue enviado a Francia.

En 1711 publicó un cuento sobre el cuento de la suerte, cuyo cuello, si hubiera sido publicado en aquel tiempo, habría sido cubierto con la recomendación de Newton: “Pregúntale a Mr. Weymouth, él sabe más que yo sobre este tema”.

No lo hizo en aquel entonces, por lo que no pudo cobrar muchos derechos de autor.

Debes recordar el problema que planteamos en el artículo anterior (Razón de riesgo: el coronel Bernoulli), para los 5000 guijarros de un cubo, podemos hacer 25.500 capturas para estimar la proporción del total de los guijarros. Pero también deberías descubrir que 25.500 capturas repetidas son demasiadas, es mejor que tirar una piedra de un número.

Utilizando el método de cálculo y el triángulo de Pascual, Montmorency adoptó un método de selección por grupos. Supone que cada vez que toma 100 guijarros de un cubo, anota la proporción de los guijarros blancos y negros y los vuelve a colocar, y luego hace la misma extracción. Con este método, Montmorency puede decirle de antemano la desviación aproximada de las proporciones registradas con respecto a las proporciones reales y cómo se distribuyen estas proporciones alrededor de sus promedios.

Sí, esa es la distribución normal con la que todos estamos familiarizados. La curva de la distribución normal es como una curva en forma de campana, la mayoría de los valores observados se agrupan en el centro, cerca de la media de todos los valores observados, y luego se inclina simétricamente hacia los extremos desde la media, y el número de valores observados en ambos extremos de la media es igual.

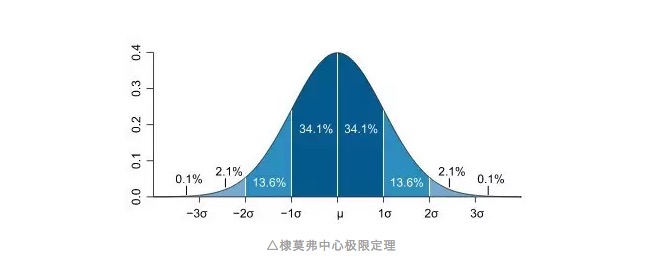
De esta manera podemos introducir el concepto de diferencia estándar, que ya hemos mencionado en otros artículos de Publicado: ¿Por qué diferencia estándar? Medidas de riesgo a los ojos de Dios. La diferencia estándar en realidad describe el grado de desviación de los valores observados con respecto a la media, o lo entendemos como la unidad de desviación de la media.

Como un piadoso creyente, Dunmore consideraba que la curva de la campana era producto de Dios. A su juicio, con tal medida podemos vencer la incertidumbre y, por lo tanto, vencer todos los riesgos, ya que la curva describe todos los fenómenos posibles y sus probabilidades, tal vez debido a la casualidad de que se producen las llamadas desviaciones, pero con el paso del tiempo, estas desviaciones ya no afectan la ley que resumimos.

En la escuela secundaria hay un tema clásico (¿por qué siempre uso el tema de la escuela secundaria?) sobre la tasa de calificación de los productos. Si para un grupo de productos, los estándares de la industria consideran que la tasa de desperdicio no supera el 0.1% es calificada, lo que significa que elegimos al azar 10.000 de los productos, de los cuales si la tasa de desperdicio no supera los 10, se califica. Pero el resultado es que de estos 10.000, finalmente aparecen 12, si en promedio la tasa de desperdicio de los productos es del 0.1%, en realidad podemos usar el método de Tom Morrow para calcular la probabilidad de que aparezcan 12 productos de desperdicio.

Pero en la mayoría de los casos, esta pregunta no tiene sentido para nosotros. Porque en realidad no sabemos cuál es la tasa de desperdicio promedio de los productos, y si la tasa de desperdicio promedio es más alta que el estándar de detección, ¿cuál es la probabilidad de que un grupo de productos pase la prueba?

Sin embargo, la mayoría de los inversores en China no están interesados en la inversión.