Relación de Sharpe 0,6, ¿debería abandonarla?

Se hace un experimento para ilustrar este problema. El experimento comienza con algunas suposiciones clave. Tenemos 20 señales de transacción que tienen un rendimiento anualizado del 8% y un Sharpe ratio anualizado del 0.6. Las señales de esta estrategia no son muy productivas.

• Una variable de entrada importante en la negociación es la correlación entre señales. Hacemos una serie de experimentos de acuerdo con un coeficiente de correlación de 0 a 0.9. Los experimentos no tienen en cuenta el costo de la negociación (ya que solo estamos interesados en el rendimiento relativo) y la distribución de la rentabilidad de la cartera anualizada, que se reequilibra diariamente según la correlación, es básicamente la misma.

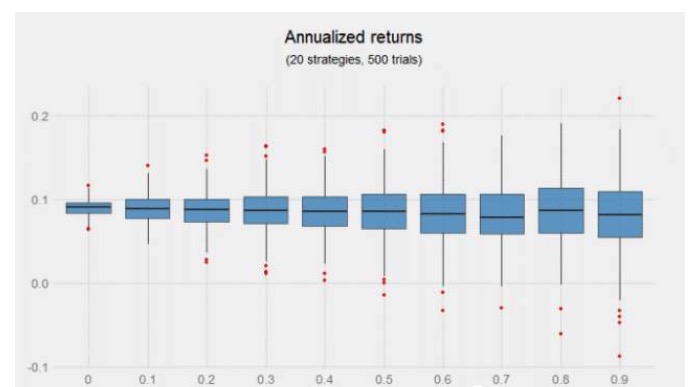
La combinación de señales de baja correlación no mejora la ganancia, pero el gráfico de arriba sugiere los beneficios que pueden traer las estrategias adicionales, especialmente cuando estas estrategias no están relacionadas. En la mitad izquierda de la gráfica, es decir, el coeficiente de correlación de 0 a 0.4, la distribución es más estrecha y la ganancia de los quinientos experimentos es positiva.

Los resultados son mucho más claros cuando se utiliza la proporción de Sharpe para medir los beneficios ajustados al riesgo. Al combinar 20 estrategias con una proporción de Sharpe anual de 0.6 y un coeficiente de correlación 0 entre sí, se obtiene una proporción de Sharpe anual de 3, mientras que al combinar 20 estrategias con una proporción de Sharpe anual de 0.6 y un coeficiente de correlación promedio de 0.9, se obtiene una proporción de Sharpe anual de 0.64, lo que supone un rendimiento 370% mayor que la última.

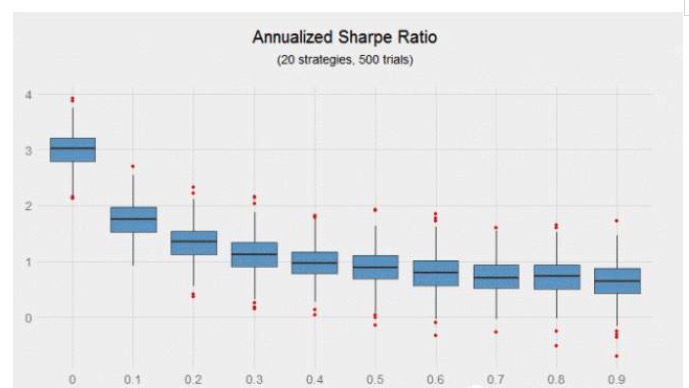
En el gráfico de arriba es notable que la tasa de Sharpe ha disminuido rápidamente a medida que aumentaba la correlación de las estrategias. La tasa de Sharpe ha disminuido un 56% cuando el coeficiente correlativo aumenta de 0 a 0.2.

Incluso con un Sharpe ratio muy alto, esta estrategia de combinación tiene casi 50 000 señales de transacción, la diferencia en el Sharpe ratio de una combinación de correlación cero es sorprendente. Un inversionista afortunado puede obtener un Sharpe ratio de 3.5 (que puede hacer a una persona multimillonaria) mientras que un inversionista desafortunado que tiene la misma combinación solo obtiene un Sharpe ratio de 2.5. Incluso en una combinación de alta Sharpe ratio, la suerte juega un papel importante.

Obviamente, cuantas más muestras de observación hay, más claras son las fronteras. ¿Qué ocurriría si un inversionista solo tuviera una muestra de observación de un año en lugar de una de un decenio? La siguiente gráfica muestra que a medida que aumenta la relevancia, la diferencia en la proporción de Sharpe aumenta exponencialmente.

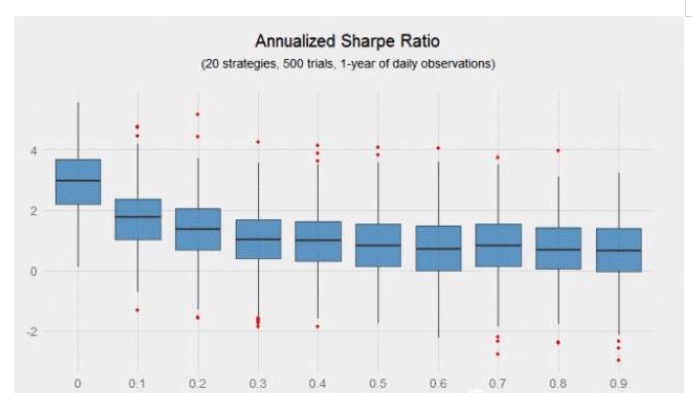
Si simuláramos 10000 de las estrategias individuales mencionadas, ¿qué proporción de la p-valor de prueba es inferior al 5%? La respuesta es cerca del 48%, lo que podría llevar a la mayoría de los investigadores a abandonar esta estrategia cotidiana (es decir, la estrategia de la tasa de Sharpe anual de 0.6). Sin embargo, si la correlación entre las señales es lo suficientemente baja, combinar estas señales débiles puede producir milagros, y el flujo de retorno de la combinación puede ser muy notable.

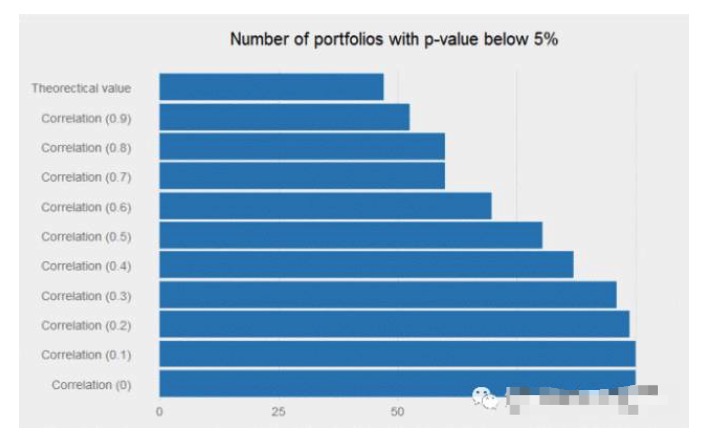
Una estrategia de un Sharpe ratio anual de 0.6 puede ser descartada por los investigadores porque no tiene ningún atractivo en las transacciones. Pero si tiene la correlación correcta (es decir, baja) entre las señales existentes, puede aumentar el valor de la cartera.

Este artículo no abre un nuevo campo, ya que los beneficios de la inversión descentralizada son bien conocidos en la comunidad de inversionistas. Pero sí te recuerda que no es necesario renunciar a una estrategia de un índice anual de Sharpe de 0.6, tal vez puedas agregarla a tu cartera de estrategias existentes, lo que reduce la liquidez de la cartera y permite el uso de más palanca para aumentar los ingresos totales.

Traducido y adaptado de la obra privada