Los puerros y el diferencial entre oferta y demanda: un estudio preliminar sobre el modelo EKOP

• #### 1 Se inicia

He estado muy ocupado últimamente, ya han pasado meses desde la última vez que escribí una columna. Estos meses han sido llenos de cosas, algunas de las cuales han sido ciertamente oscuras para mi propia vida. Sin embargo, estas experiencias me han enseñado que la vida, como el comercio, tiene altibajos y está llena de lo desconocido. Siempre esperamos poder aprender algo de lo que ha sucedido, acercándonos lentamente a una verdad que tal vez no exista.

Todos sabemos que una acción que está activamente negociada suele tener un diferencial de compra y venta más pequeño, mientras que una acción que no está activamente negociada tiene el contrario. ¿Por qué ocurre esto? ¿Se puede explicar la diferencia de precios con un modelo matemático simple y bonito?[1] La idea inicial fue investigar si el comportamiento de los operadores con información diferente era la causa de la diferencia entre las dos clases de precios de las acciones. En esta columna, presentaré las bases de este modelo. La aplicación del modelo se analizará más a fondo en artículos posteriores (si tengo tiempo para escribir). La belleza de la simplicidad de los modelos matemáticos se exhibe en este artículo.

• #### 2 Las hipótesis del proceso de transacción

Cuando hablamos de un modelo financiero, lo más importante es prestar atención a las hipótesis de este modelo. Un buen modelo financiero tiene sus propias hipótesis: no es tan fuerte que no sea universal; ni es tan débil que no pueda derivar resultados bonitos y concisos.

Suposición 1: Hablamos de acciones que se negocian en días separados y continuos. Es decir, las operaciones de los operadores ocurren en 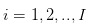en estos días separados. Y en el día de negociación, las operaciones ocurren en 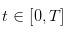en este tiempo continuo.

• La mala noticia es que hemos registrado el valor de las acciones en
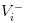
• La buena noticia es que hemos registrado el valor de las acciones como
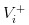
• No hay noticias, y el valor de las acciones es

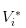
Es obvio que tenemos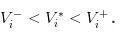

Suposición 2: En un día dado, hay un

La probabilidad de que ocurra un evento que afecte el precio de las acciones es de 1-α, mientras que la probabilidad de que no ocurra un evento que afecte el precio de las acciones es de 1-α. En los días en que ocurren los eventos, hay una probabilidad de que ocurra un evento malo que haga que el precio de las acciones baje, y una probabilidad de que ocurra un evento bueno que haga que el precio de las acciones suba.

Hipótesis 3: Los participantes en el comercio de acciones son los creadores de mercado (market makers, abreviado MM), los comerciantes informados (informed traders, abreviado IT), y los comerciantes no informados (uninformed traders, abreviado UT). Se comportan de la siguiente manera:

MM siempre está listo para poner una oferta de compra o venta de una unidad, cumpliendo con su obligación como comerciante de mercado. MM es neutral en cuanto al riesgo, por lo que el precio que pone es el precio justo que él considera.

IT solo opera en los días de noticias, su comportamiento comercial es un proceso de reposo. En un día determinado, si ocurren malas noticias, coloca una oferta a una tasa de llegada de μ; y en los días de buenas noticias, coloca una oferta a una tasa de llegada de μ.

UT, es decir, nuestros pobres espinacas, debido a la ventaja de no tener noticias, su comportamiento de negociación es también un proceso de suspensión, en el que cada día, se suspenden las compras y las ventas en la tasa de llegada. Tenga en cuenta que todos los procesos de positrón son independientes entre sí. Podemos representar la hipótesis 3 con un gráfico, como sigue:

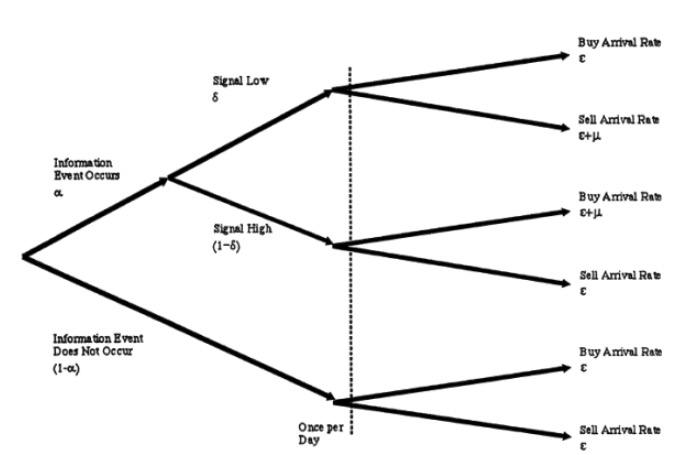
• #### 3 Actualización de transacciones y precios

Sabemos que los comerciantes de mercado suelen ser las grandes empresas que trabajan de forma brusca. Son muy inteligentes, y en el proceso de luchar contra la TI y la UT a largo plazo, resumieron todos los parámetros del modelo en este diagrama de árbol arriba a través de un gran número de análisis de datos históricos. Afortunadamente, no son tan inteligentes como los comerciantes de información, cuando un día de negociación está a punto de abrir, no saben como los comerciantes de información, si algo importante sucedió hoy.

Ahora, vamos a experimentar el papel de un MM, luchando con TI y TI. En un momento dado en t, nos marcamos a nosotros mismos como un vector en la conjetura de la probabilidad de que ocurra algo bueno o malo.

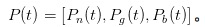。 Obviamente, al comienzo del día, es decir, cuando /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, no vi un solo informe, así que todo lo que puedo hacer es pensar que la probabilidad de que nada ocurra es α, la probabilidad de que algo bueno ocurra es /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, y la probabilidad de que algo malo ocurra es /upload/asset/87418f07b12f65cef4c3f70b24e0d94e2f19769a.png.

¿Cómo actualizar esta probabilidad? Bueno, todos los que hacemos elecciones en el mercado conocemos la fórmula de Bayes. Cuando observamos una venta, usamos la ley de Bayes para actualizar nuestra propia estimación de probabilidad.

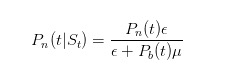
La molécula de esta fórmula dice que cuando no hay noticias, sólo el comerciante ignorante venderá con una letra ε; y el denominador dice que en cualquier momento, el comerciante ignorante venderá con una letra ε, y el comerciante informado venderá con una letra μ sólo cuando ocurra algo malo. De manera similar, podemos deducir

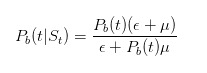
y

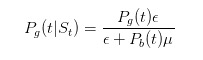
Antes de continuar con la deducción, vamos a hacer algunas pruebas simples. Dijimos que si vemos una factura de venta, entonces nuestra estimación de la probabilidad de que ocurra algo malo debería aumentar.

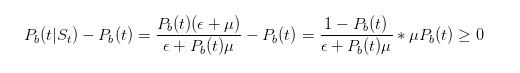
Por lo tanto, nuestra inferencia confirma nuestra intuición.

Ahora, con la probabilidad actualizada, podemos calcular el precio justo como el precio de compra que hacemos en el mercado, expresado como

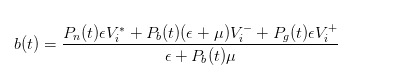
A través de una deducción similar, podemos ver que cuando un pedido de compra llega, el precio de venta que nosotros, como comerciantes, reportamos debería ser

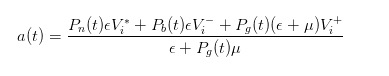
• #### 4 Expresión de la diferencia de precio después de la transformación del precio

La expresión de precios de compra y venta no es lo suficientemente intuitiva, podemos introducir el valor esperado de la acción en el momento t para simplificar la expresión. Tenemos un valor esperado de

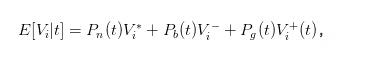
Así que podemos transformar las expresiones de la oferta y la demanda en

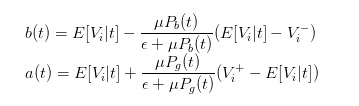
Por lo tanto, podemos expresar claramente la diferencia de precios como

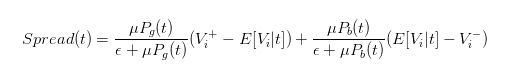
• #### 5 El efecto de la conducta de los comerciantes en las diferencias de precios

Con la expresión de la diferencia de precios, podemos analizar el impacto de los diferentes comerciantes en la diferencia de precios.

Cuantas más espinacas, menor será la diferencia de precios. Tenga en cuenta que ε es la tasa de llegada de los comerciantes ignorantes (llamémoslos espinacas) y si hay ε >> μ, podemos encontrar que / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png ambos se acercarán a 0, lo que significa que el spread también se acercará a cero. Si vamos al otro extremo, suponiendo que el mercado no tenga espinacas, solo hay un grupo de comerciantes informados que son mejores que los espinacas, entonces descubriremos lamentablemente que los precios que publicamos serán 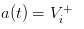y /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, por lo que los comerciantes informados se encuentran sin ganancias independientemente de la forma en que se compre o se venda, y el mercado inevitablemente se desvanecerá.

Verás, basándonos en algunas hipótesis, usando una deducción matemática muy simple, podemos llegar a conclusiones tan interesantes y profundas, y eso es probablemente el gran atractivo de los modelos matemáticos.

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.