Cobertura delta de opciones de Bitcoin usando la curva de la sonrisa

resumen

Analizamos la cobertura delta dinámica robusta de opciones de Bitcoin utilizando un conjunto de curvas de sonrisa implícitas y otros deltas ajustados por sonrisa. Estos deltas no dependen del modelo, en el sentido de que son los mismos para cada modelo de volatilidad estocástica y/o local invariante de escala, o se basan en simples parametrizaciones dependientes del régimen de la volatilidad local. Estos deltas son populares entre los creadores de mercado en los mercados de opciones para activos tradicionales porque son fáciles de implementar. Las investigaciones empíricas anteriores sobre la cobertura delta dinámica se han basado únicamente en opciones sobre índices bursátiles, pero el análisis de datos únicos sobre los precios históricos por hora de las opciones de Bitcoin muestra que el comportamiento de la curva de volatilidad implícita de Bitcoin es muy diferente al de las opciones sobre índices bursátiles. Para opciones de compra y venta con un amplio universo de financiamiento y vencimientos fijos sintéticos de 10, 20 y 30 días, comparamos el desempeño de cobertura dinámica de diferentes deltas ajustados por smile durante dos períodos de un año. También investigamos el uso de contratos perpetuos en lugar de futuros estándar como instrumento de cobertura, ya que el riesgo base de los contratos perpetuos es mucho menor que el de los futuros calendario. Los resultados se presentan como una estadística comprobable de la relación de varianza del error cubierto. En ciertos períodos, el uso de la relación de cobertura de curva de sonrisa implícita puede superar significativamente la simple cobertura Delta de Black-Scholes, especialmente cuando se utilizan swaps perpetuos como herramienta de cobertura, la ganancia de eficiencia de las opciones de venta fuera del dinero puede superar el 30%. Mientras que en la cobertura de opciones de compra fuera del dinero a corto plazo durante períodos de curvas de volatilidad implícita con pendiente ascendente, las ganancias de eficiencia promedio pueden alcanzar el 15%. Las ventajas de utilizar contratos perpetuos son especialmente evidentes en 2021, especialmente en el caso de los contratos a largo plazo en los que la base sigue siendo bastante amplia.

Palabras clave ：Cobertura de derivados, curva de volatilidad implícita, contratos perpetuos, financiación robusta, cobertura incremental dinámica

1. Introducción

Cualquier investigación sobre cobertura delta dinámica se basa en el modelo de Black y Scholes (1973). El delta de Black-Scholes (BS) solo requiere derivadas parciales del precio de la opción del modelo con respecto al precio subyacente, ya que el modelo supone que la correlación entre el precio subyacente y su volatilidad es cero. Sin embargo, es bien sabido que las opciones sobre índices bursátiles tienen una correlación precio-volatilidad grande y negativa, lo que conduce a una asimetría significativa en la curva de volatilidad implícita. Siguiendo la idea básica de Bates (2005) y los resultados más generales de Alexander y Nogueira (2007a), la pendiente de la curva de volatilidad implícita se puede utilizar para implicar ajustes al Delta BS, que es independiente del modelo, es decir, Es constante para cualquier escala independiente. Los modelos variantes son los mismos. Sin embargo, Alexander y Nogueira (2007b) muestran que, para los instrumentos negociables (distintos de las tasas de interés), todos los modelos de fijación de precios de opciones sobre acciones basados ​​en volatilidad estocástica y/o local deberían ser invariantes en escala, independientemente de factores adicionales como saltos o procesos de Lévy. Las características son: Por lo tanto, cualquier diferencia entre el desempeño de cobertura empírica de los dos modelos de volatilidad paramétrica (para instrumentos negociables) se debe simplemente a que los modelos tienen diferentes errores de calibración. La derivada parcial delta (en realidad gamma) del precio de la opción con respecto al precio del instrumento negociable es teóricamente exactamente la misma que la delta invariante de escala libre del modelo. Nota 1 Además, el Delta simple invariante de escala propuesto por Bates (2005) es mayor (menor) que el Delta de BS cuando la pendiente de la curva de sonrisa es negativa (positiva). Dado que Coleman et al. (2001) muestran que el delta BS tiende a estar sobrecubierto en un marco de volatilidad local, cuando la volatilidad implícita está sesgada negativamente, el delta invariante de escala estará más sobrecubierto que el delta BS.

Como lo describen Alexander y Nogueira (2007a), la derivada total de varianza mínima (MV) con respecto al precio es otro delta que tiene en cuenta correlaciones precio-volatilidad distintas de cero, pero depende del modelo. Sin embargo, estos autores no pudieron distinguir entre los resultados empíricos obtenidos utilizando el MV Delta sin modelo de Lee (2001) y el MV Delta basado en diferentes modelos invariantes de escala. El MV Delta de Lee (2001) también está “ajustado por sonrisa”, es decir, agrega un término al delta de BS que se calibra utilizando las características empíricas de la curva de sonrisa de volatilidad implícita. Otra forma de ajustar el Delta BS es utilizar el enfoque propuesto en el trabajo seminal Smile-Adjusted Delta de Derman y Kani (1994) y Derman (1999) agregando un término que captura la correlación precio-volatilidad. Estos no son completamente libres de modelos, ya que el término de ajuste depende de la parametrización de la volatilidad local, que a su vez depende del régimen prevaleciente en el mercado. Sin embargo, no dependen de modelos en el sentido de que no se hacen suposiciones sobre los procesos que impulsan la evolución del precio subyacente, como la difusión de saltos de volatilidad local estocástica, y no hay parámetros que deban calibrarse utilizando precios de opciones y/o datos históricos subyacentes. datos.

Es una práctica habitual que los creadores de mercado de opciones sobre acciones cubran su exposición utilizando simples ajustes libres de modelos al BS Delta, ya que estos se consideran lo que se denomina una “financiación robusta”, es decir, que el ratio de cobertura es independiente del modelo. Las curvas de sonrisa implícitas y otras coberturas delta ajustadas por curva de sonrisa son particularmente populares entre los profesionales, como lo evidencian numerosos artículos y foros. Nota 2: Hay varios estudios empíricos previos sobre la cobertura delta de curvas de sonrisa implícitas y/o curvas ajustadas por sonrisa, pero todos ellos estudiaron opciones sobre índices de acciones. No todos los resultados son consistentes: Vähämaa (2004) muestra que algunos deltas ajustados por curva sonriente superan a los deltas BS para las opciones FTSE 100, pero solo durante períodos de volatilidad excesiva; Crépey (2004) confirma que estos resultados se aplican a las opciones DAX 30; Attie ( 2017) afirma que el delta implícito en la sonrisa supera consistentemente al delta BS en la cobertura de opciones del índice S&P 500; Alexander et al. (2012) extienden el marco de Derman (1999) a una configuración de conmutación de Markov para reflejar el Delta ajustado por sonrisa correcto aplicable al actual régimen de mercado, mostrando que para las opciones del S&P 500, BS Delta solo se puede mejorar utilizando esta extensión de conmutación de Markov; François y Stentoft (2021) también estudiaron las opciones del índice S&P 500 y confirman que los ajustes estándar no pueden superar a BS delta o delta-gamma coberturas, pero su nueva cobertura delta-gamma-vega de curva sonriente implícita mejora significativamente el modelo BS. Se sabe poco sobre el éxito de la cobertura delta ajustada por sonrisa con respecto a otros tipos de opciones. Nota 3

El propósito de este artículo es examinar el desempeño de la cobertura delta de varias curvas implícitas de Smile y otras curvas ajustadas de Smile aplicadas a las opciones de Bitcoin. Al momento de escribir este artículo, solo ha aparecido una pequeña cantidad de investigaciones sobre las opciones de Bitcoin. Siu y Elliott (2021), Jalan et al. (2021) y Chen y Huang (2021) estudian las aplicaciones empíricas de los modelos de fijación de precios de volatilidad estocástica, pero ninguno de los artículos estudia su rendimiento de cobertura. Hou et al. (2020) consideraron una serie de modelos de volatilidad estocástica para fijar el precio de las opciones de Bitcoin. Los autores presentan un conjunto de resultados importantes que resaltan la importancia de los saltos y co-saltos y proponen un modelo de volatilidad estocástica con saltos correlacionados (SVCJ) para fijar el precio de las opciones de Bitcoin. Estos modelos son muy útiles para fijar el precio de opciones exóticas como las opciones cliquet o ratchet. Aunque Chi y Hao (2021) consideran estrategias de cobertura delta basadas en GARCH, su investigación se centra en comparar diferentes modelos de pronóstico de volatilidad realizada. Alexander et al. (2022b) estudian el comportamiento de la curva de sonrisa de volatilidad implícita para las opciones de Bitcoin para inferir si la presión de demanda de los creadores de mercado está impulsada por operadores direccionales o operadores de volatilidad. De hecho, hasta donde sabemos, solo existe otro estudio detallado sobre la cobertura de opciones de Bitcoin (Matic et al., 2021), y utiliza un enfoque completamente diferente al de este artículo. Matic et al. (2021) utilizan la volatilidad implícita diaria cotizada por la bolsa Deribit para calibrar la superficie de volatilidad implícita inspirada en la volatilidad estocástica paramétrica y luego interpolan la volatilidad implícita de las opciones entre uno y tres meses de manera libre de arbitraje. Volatilidad. La muestra entre abril de 2019 y marzo de 2020 se divide luego en tres subperíodos (mercado alcista, mercado tranquilo y período COVID) utilizando el proceso de volatilidad estocástica introducido por Duffie et al. (2000) y McNeil y Frey (2000). Densidad del kernel del filtro GARCH para modelar los precios de las criptomonedas subyacentes. Luego comparan el desempeño de cobertura de los bonos del Tesoro griegos con el derivado de varios modelos de difusión de salto de volatilidad estocástica. Para las opciones con vencimiento a un mes, los autores no encuentran mejoras significativas sobre la cobertura BS simple, pero para las opciones con vencimiento a tres meses, los modelos más complejos mejoran significativamente el rendimiento de la cobertura.

A diferencia de Matic et al. (2021), no comparamos el desempeño de la cobertura de opciones de diferentes modelos de volatilidad estocástica. Una ventaja práctica importante de nuestro estudio es que todos los valores Delta son muy fáciles de calcular. Dado que toda la información se deriva de la curva de sonrisa de volatilidad de una manera directa y robusta sin necesidad de modelos, no se requiere calibración del modelo. Resultados de nuestra Cobertura Delta utilizando diferentes ajustes del Delta de BS dependiendo de las condiciones actuales del mercado, la forma de la sonrisa de volatilidad implícita y/o la correlación precio-volatilidad.

Nos centramos en opciones a corto plazo con vencimientos de 10 a 30 días, que tienen una liquidez mucho mayor y un rango más amplio de precios de ejercicio que las opciones estudiadas en Matic et al. (2021). Elegimos hacer esto porque las opciones de Bitcoin con fechas de vencimiento entre uno y tres meses solo representan el 20% del volumen total de operaciones, mientras que las opciones con fechas de vencimiento de 30 días o menos representan el 50% del volumen total de operaciones. Aproximadamente el 80% de todas las opciones de Bitcoin con fechas de vencimiento entre uno y tres meses solo representan el 20% del volumen total de operaciones, mientras que las opciones con fechas de vencimiento de 30 días o menos representan el 50% del volumen total de operaciones. Volumen de comercio. Además, necesitamos una curva de sonrisa adecuada para ajustar la sonrisa al delta BS, y el rango de impacto líquido de estas opciones a corto plazo es bastante grande. De hecho, el valor monetario de las opciones utilizadas en nuestro análisis empírico varía entre 0,7 y 1,3.

Solo analizamos la cobertura delta dinámica con reequilibrio regular, que ocurre cada ocho horas en el momento de la financiación o diariamente a las 00:00 UTC. La elección de este diseño experimental se basa en las características del mercado de opciones de Bitcoin, que son novedosas y por lo tanto se explican en detalle más adelante. Los costos de transacción de los futuros son mucho menores que los de las opciones. Por ejemplo, los contratos de futuros tienen diferenciales que van desde aproximadamente 1 a 5 puntos básicos, dependiendo de la fecha de vencimiento, pero las opciones at-the-money a corto plazo, que a menudo se utilizan para la cobertura gamma, suelen tener diferenciales de aproximadamente 200 a 300 puntos básicos. agujas. Por lo tanto, la cobertura gamma es mucho más costosa que la cobertura delta dinámica regular. Los costos de transacción de reequilibrar una cobertura gamma pueden erosionar cualquier ganancia obtenida al reducir el error de cobertura, mientras que los costos de transacción de reequilibrar una cobertura delta son pequeños, especialmente cuando se utilizan contratos perpetuos como instrumento de cobertura.

A continuación, la Sección 2 describe el mercado de opciones y futuros de Bitcoin; la Sección 3 compara las características de las superficies de volatilidad implícitas para Bitcoin y los índices bursátiles y distingue sus características; la Sección 4 describe nuestro marco empírico. Cada ratio de cobertura se presenta como una fórmula de BS ajustada. ; La sección 5 describe nuestros datos; la sección 6 presenta los resultados empíricos; y la sección 7 concluye.

2. Mercados de opciones y futuros de Bitcoin

Al momento de escribir este artículo, seis importantes intercambios de criptomonedas ofrecen opciones de negociación en Bitcoin y otras monedas, así como algunos tokens, con un volumen de negociación promedio diario total cercano a los mil millones de dólares en diciembre de 2021. En particular, el volumen de operaciones en opciones de Bitcoin ha aumentado recientemente hasta alcanzar máximos históricos, con un volumen de operaciones mensual promedio que se ha más que duplicado y un interés abierto que se ha multiplicado por más de seis entre enero de 2020 y diciembre de 2021. La gran mayoría de las transacciones se realizan en la bolsa de opciones Deribit, que se trasladó a Panamá para evitar seguir los estándares internacionales establecidos por agencias gubernamentales como la Comisión de Comercio de Futuros de Productos Básicos de Estados Unidos (CFTC) o cualquier otra forma de regulación para proteger los intereses de los clientes. Al igual que muchos otros intercambios de derivados de criptomonedas no regulados, a menudo registrados en paraísos fiscales offshore, la plataforma de negociación de Deribit está abierta las 24 horas del día, los 7 días de la semana y se adhiere a pocos o ningún protocolo de “conozca a su cliente”. En Deribit se negociaron 4,3 millones de contratos (con un valor nocional de aproximadamente 55 mil millones de dólares) en 2020, y 6,2 millones de contratos (con un valor nocional de aproximadamente 290 mil millones de dólares) en 2021. Como resultado, en sólo dos años, el número de contratos listados ha aumentado en más de un 45% y el importe nocional negociado en Deribit ha aumentado en más de un 430%. Nota 4 Para poner esto en perspectiva, el mercado de opciones del S&P 500 del Chicago Board Options Exchange (CBOE) creció solo alrededor del 10% entre 2020 y 2021. Nota 5 En el mercado de opciones de Bitcoin, casi todos los meses se lanzan nuevos tamaños de contratos, rangos de precios de ejercicio más amplios, vencimientos más largos y nuevos subyacentes, lo que amplía este mercado emergente de derivados tanto a los operadores minoristas como a los institucionales. Hacer que las opciones de Bitcoin dejen de ser un producto de nicho . En marzo de 2022, la Bolsa Mercantil de Chicago (CME) lanzó micro opciones de Bitcoin en un intento de competir con las plataformas autorreguladas dirigidas a los comerciantes minoristas. Pero los grandes actores institucionales también están siguiendo muy de cerca el mercado de opciones, y algunos incluso lo llaman “el próximo gran paso”. Nota 6 Por otro lado, los protocolos emergentes de finanzas descentralizadas (DeFi) como Opyn o Ribbon Finance ofrecen negociación de opciones sin seguir ningún cumplimiento normativo. Con un volumen comercial nominal de más de 500 millones de dólares por día, este ya no es un mercado que los inversores tradicionales puedan ignorar.

El gran volumen de operaciones en Deribit lo convierte en el intercambio más atractivo para cualquier tipo de investigación de opciones de criptomonedas. Si bien CME (y algunos otros exchanges) solo listan opciones de Bitcoin, solo entre el 10% y el 15% del volumen de operaciones de opciones de Bitcoin puede atribuirse a estos exchanges. Deribit por sí solo representa más del 90% del volumen de negociación de opciones de Bitcoin. Nota 7 Una razón podría ser que Deribit opera 24 horas al día, 7 días a la semana, mientras que CME sólo opera los días de semana. Otra razón podría ser que las opciones de Deribit tienen margen y se liquidan en Bitcoin, aunque su subyacente es el valor en USD del índice BTC. Para obtener el pago al vencimiento, se calcula la diferencia entre el valor de BTC en USD y el precio de ejercicio de la opción (también cotizado en USD) y el resultado se convierte a Bitcoin utilizando el valor del índice BTC al vencimiento. Nota 8 La diferencia en unidades monetarias entre el precio de liquidación (es decir, Bitcoin) y el subyacente (es decir, USD) es muy similar al pago de una opción FX cuantitativa, excepto que no hay futuros ni opciones en la dirección opuesta. Es decir, no existen derivados sobre el valor de un dólar de Bitcoin, ni tampoco existen opciones que utilicen el valor de un dólar de Bitcoin como subyacente. Por esta razón, las opciones de Bitcoin se denominan “opciones inversas” y, de hecho, son solo uno de varios productos derivados inversos, incluidos los futuros inversos, que se negocian intensamente en muchas bolsas de derivados de criptomonedas. Son atractivos porque las operaciones con derivados en cruces de monedas fiduciarias y criptográficas se pueden realizar sin utilizar moneda fiduciaria como garantía en una cuenta de margen o para la liquidación de contratos.

Si Bitcoin puede existir como un mercado monetario en el sentido tradicional es un tema de debate (Sauer, 2016), pero existen mercados monetarios descentralizados altamente activos para Bitcoin (y otras monedas y tokens) en muchos sitios de cultivo y diferentes grupos de liquidez. Nota 9 Por lo tanto, podemos convertir de USD a Bitcoin para medir el efecto de cobertura de cualquier modelo en USD.

Independientemente del método de cobertura que elija, la cobertura en sí es sencilla. El comerciante abre una posición en una opción y toma una posición opuesta en el activo subyacente con un tamaño de posición igual al valor delta de la opción. En los mercados tradicionales, el instrumento de cobertura suele ser un contrato de futuros con el mismo vencimiento que la opción, ya que el precio de liquidación no es un instrumento fácilmente negociable. Para el índice BTC, dado que se basa en un promedio de los precios de Bitcoin en varios intercambios diferentes, se aplican los mismos comentarios. Pero esto no significa que el instrumento de cobertura deba ser un contrato de futuros inverso con el mismo vencimiento que la opción, ya que existen algunas alternativas innovadoras para elegir instrumentos de cobertura negociables en Bitcoin. En primer lugar, hay tres tipos diferentes de contratos de futuros con fecha finita: futuros lineales estándar, que no son diferentes de los futuros sobre clases de activos tradicionales; futuros lineales sobre Bitcoin contra monedas estables en USD (como Tether), que se negocian siempre que el precio de la moneda estable se desvía. de su paridad con el dólar estadounidense, lo que introduce un riesgo de base; y los futuros inversos, que tienen propiedades similares a los futuros lineales del dólar estadounidense pero están marginados y liquidados como las criptomonedas. Nota 10

Las opciones de Bitcoin también tienen una herramienta de cobertura que utiliza contratos exclusivos del mercado de criptomonedas. Estos contratos a menudo se denominan futuros perpetuos, swaps perpetuos o simplemente “contratos perpetuos” y son, con diferencia, el tipo de derivados de criptomonedas más popular. Sus precios están estrechamente ligados al spot, utilizando un mecanismo de “financiación” que paga o recibe automáticamente una pequeña porción de la posición neta cada ocho horas. El cálculo de este porcentaje, llamado “tasa de financiación”, varía de una bolsa a otra. Nota 11 El pagador y el receptor dependen de si el precio del contrato perpetuo es mayor o menor que el precio al contado (BTC). Cuando el precio del contrato perpetuo es superior al precio al contado, la tasa de financiación es positiva y los usuarios que mantienen posiciones largas en contratos perpetuos deben pagar tarifas, mientras que los usuarios que mantienen posiciones cortas reciben tarifas. Lo contrario ocurre cuando el precio del contrato perpetuo es inferior al precio al contado. Los pagos de financiación regulares entre posiciones largas y cortas mantienen el precio del contrato perpetuo muy cerca del precio al contado.

En Binance, la bolsa de derivados y al contado de criptomonedas más grande del mundo, dos tercios de los productos negociados son contratos de futuros perpetuos. Esta relación entre el spot y los derivados parece ser estándar en el mercado de criptomonedas, como lo muestra el informe CryptoCompare (2022). Al momento de escribir este artículo, ocho intercambios de criptomonedas informan volúmenes promedio diarios de transacciones de futuros que superan los mil millones de dólares, y la mayoría de ellos son atribuibles a contratos perpetuos. Nota 12 Aquí, los intercambios no regulados como Binance, OKEx y Bybit representan más del 65% de todas las transacciones de futuros. Por el contrario, las bolsas reguladas, en particular CME y FTX US, tienen una participación de mercado mucho menor, de alrededor del 25%. Los futuros de Deribit tienen un volumen comercial diario promedio de más de $4 mil millones, lo que proporciona suficiente liquidez para considerar estos futuros como instrumentos de cobertura adecuados. Sin embargo, como ocurre en otros mercados, la mayoría de las transacciones se realizan mediante contratos perpetuos en lugar de futuros calendario. Para ver esto, la Figura 1 muestra los montos comerciales nocionales de estos contratos registrados diariamente pero suavizados utilizando un promedio móvil de 7 días durante un período de dos años a partir de enero de 2020. Es evidente que los contratos de futuros perpetuos tienen mucho más volumen que los contratos de futuros con fecha de vencimiento finita, aunque para estos últimos hemos agregado datos de volumen diario para los tres tipos de futuros, así como datos para cada fecha de vencimiento. En 2021, el volumen de negociación de contratos perpetuos casi se cuadriplicó con respecto al año anterior. El cuadro 1 demuestra empíricamente esta evolución de los volúmenes de comercio. Muestra el volumen diario promedio y el interés abierto de los tres principales derivados de Bitcoin en el intercambio Deribit. Los volúmenes y el interés abierto en todos los productos aumentaron significativamente entre 2020 y 2021, probablemente debido al interés en el espacio criptográfico por parte de los principales bancos y empresas comerciales propietarias.

Figura 1. Volumen comercial diario promedio de contratos perpetuos y de futuros de Deribit.

La figura 1 muestra el volumen diario promedio de los contratos perpetuos (azul) y el volumen total promedio de todos los demás contratos de futuros (rojo) desde enero de 2020 hasta enero de 2022. El volumen diario se calcula multiplicando el número total de contratos negociados en Deribit en un período de 24 horas por su valor nominal de $10 y luego tomando el promedio de los últimos siete días. Los resultados están en miles de millones de dólares estadounidenses.

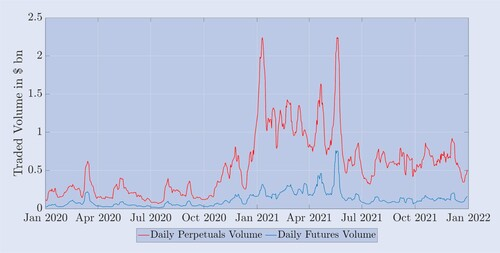
Tabla 1. Volumen e interés abierto de los derivados de Bitcoin de Deribit.

3. Volatilidad implícita de Bitcoin

La Figura 2 ilustra la dinámica empírica de la curva de volatilidad implícita derivada de las opciones de Deribit, trazada durante un período de dos años y medio en una estructura diaria. El eje de monetización representa la curva de volatilidad implícita en el precio de las opciones de compra fuera del dinero a las opciones de venta fuera del dinero, donde la monetización de las opciones de venta muy fuera del dinero es 0,7, El grado de monetización de las opciones de compra muy fuera del dinero es de 1,3, y el grado de monetización de las opciones en el dinero es de 1,3. Tanto las opciones de compra como las de venta tienen un grado de monetización de 1, e interpolamos los datos para representar estos niveles de monetización en un período de vencimiento fijo de 30 días. En la siguiente sección se ofrecen más detalles sobre los datos y su filtrado.

Figura 2. Curva de volatilidad implícita de Bitcoin.

Curva de volatilidad implícita para opciones de Bitcoin con un período de vencimiento constante de 30 días, que cubre datos diarios desde el 1 de enero de 2020 hasta el 30 de junio de 2022, derivada de opciones fuera del dinero y en el dinero. Los precios de ejercicio varían desde un 30% por debajo hasta un 30% por encima del valor actual del índice subyacente de Bitcoin.

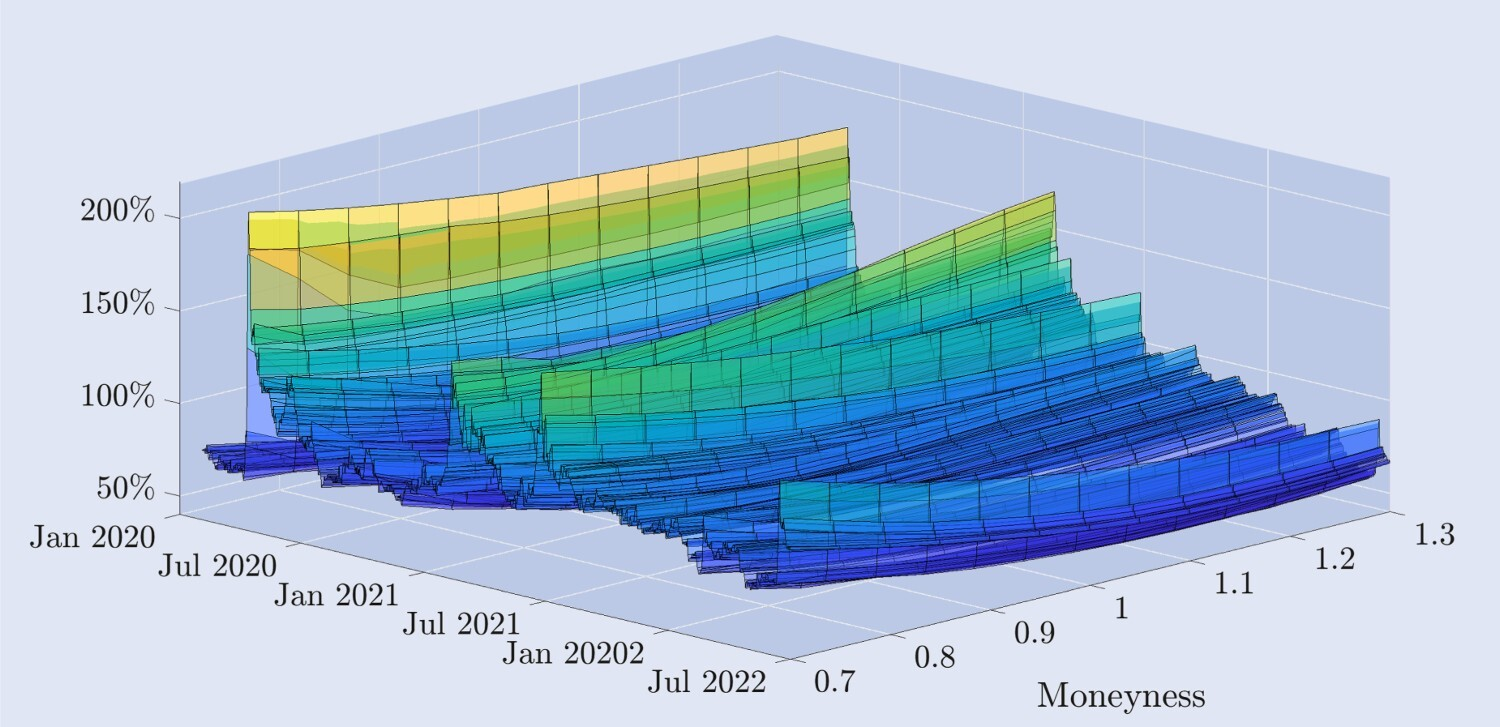
La forma de la curva varía mucho con el tiempo. Poco después del evento del “Jueves Negro” en marzo de 2020, cuando el precio de Bitcoin cayó más del 30% en unas pocas horas, la curva de volatilidad implícita adoptó una forma sesgada negativamente, lo cual es típico de las opciones sobre índices bursátiles. Es decir, La volatilidad de las opciones de venta fuera del dinero es mucho mayor que la de las opciones de compra fuera del dinero. Sin embargo, en general, las opciones de Bitcoin tienen una volatilidad implícita mucho mayor que las opciones sobre índices bursátiles. Durante la mayor parte del período de muestra, la curva de volatilidad implícita presenta una forma de “palo de hockey”, mientras que durante períodos particularmente tranquilos se aplana formando una ligera sonrisa simétrica. También hay casos de sesgo positivo, donde la volatilidad de las opciones call fuera del dinero es mucho mayor que la de las opciones put fuera del dinero. Estas características no son comunes en el mercado de opciones sobre índices bursátiles, donde a menudo se utiliza el término “sesgo” en lugar de “sonrisa” para describirlas. Para respaldar este punto, la Figura 3 proporciona otra vista de la sonrisa de volatilidad implícita. Muestra la volatilidad implícita de Bitcoin en diferentes niveles de dinero (gráfico superior), así como la desviación de la volatilidad ATM, es decir, la diferencia entre la volatilidad de dinero fijo y la volatilidad ATM (gráfico inferior). En la mayoría de las muestras, las opciones de venta fuera del dinero con un valor monetario de 0,7 tienen la volatilidad implícita más alta. En los mercados bursátiles tradicionales, estas opciones de venta muy fuera del dinero son un seguro atractivo contra la caída de los precios de las acciones. Por ejemplo, en el S&P 500, la forma pronunciada y casi linealmente sesgada de la curva de volatilidad implícita significa que las opciones que más suben de precio después de una caída del activo subyacente son aquellas con menor valor monetario. Por el contrario, la Figura 3 muestra que antes de la caída del 12 de marzo de 2020, la curva de volatilidad implícita de Bitcoin era relativamente simétrica. Las opciones ATM tienen la volatilidad más baja, alrededor del 50%, mientras que las opciones de venta fuera del dinero y las opciones de compra fuera del dinero tienen aproximadamente la misma volatilidad, pero ambas son más altas, con una volatilidad de las opciones de 0,7 y 1,3. alrededor del 75%. Sin embargo, en el colapso hubo una clara sonrisa asimétrica, ya que las opciones de venta fuera del dinero generaron primas más altas para los inversores reacios al riesgo en caso de que los precios cayeran bruscamente nuevamente. La volatilidad implícita de las opciones de venta a 30 días muy fuera del dinero aumentó repentinamente a casi el 200%. Bitcoin ha experimentado una clara tendencia negativa por primera vez, pero la forma sigue siendo mucho más plana en relación con las formas sesgadas que se observan típicamente en las opciones sobre índices bursátiles. Esta asimetría persiste, pero a medida que el nivel de volatilidad implícita disminuye, la forma de la curva de volatilidad implícita comienza a tomar nuevamente la forma de una sonrisa.

Figura 3. Volatilidad implícita de Bitcoin y sesgo de cajero automático.

La figura muestra la curva de volatilidad implícita para las opciones de Bitcoin con un plazo de 30 días y un rango de tiempo del 1 de enero de 2020 al 30 de junio de 2022. La curva se calcula utilizando opciones out-of-the-money y at-the-money, con precios de ejercicio que van desde una caída del 30% hasta un aumento del 30% en el valor actual del índice Bitcoin.

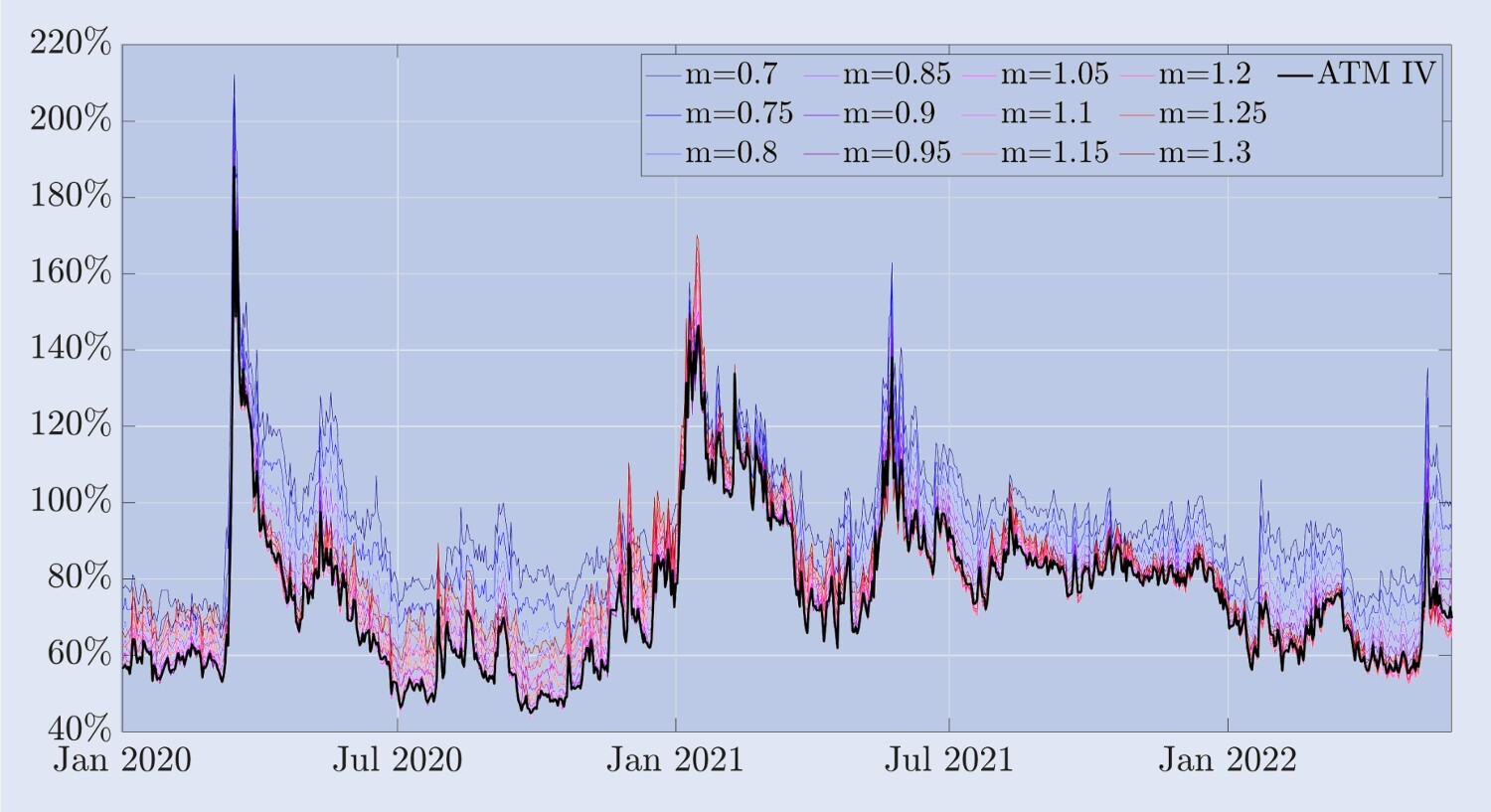
Con base en nuestros datos de muestra, la volatilidad implícita en ATM (at the money) parece ser el punto más bajo de la curva de la sonrisa y está sesgada negativamente la mayor parte del tiempo. Sin embargo, a diferencia de las opciones sobre índices bursátiles, la curva sonriente muestra una asimetría positiva significativa durante períodos de alta volatilidad. Por ejemplo, durante el repunte de Bitcoin en junio de 2021, la pendiente de la curva de la sonrisa aumentó y se mantuvo sesgada positivamente durante varios meses. Si bien la correlación entre los precios de los índices bursátiles y la volatilidad es casi siempre grande y negativa, la correlación entre los precios de Bitcoin y su volatilidad implícita parece depender de las condiciones del mercado. De agosto de 2019 a noviembre de 2020, la correlación entre el precio de Bitcoin y la volatilidad implícita de ATM de 30 días fue de aproximadamente -0,42; en los siguientes cinco meses, la correlación aumentó a 0,74; y en 2022 De julio a noviembre de 2017, la correlación entre el precio y la volatilidad implícita de ATM de 30 días fue de aproximadamente -0,42; en los siguientes cinco meses, la correlación aumentó a 0,74; y en 2022 La volatilidad fue de 0,08.

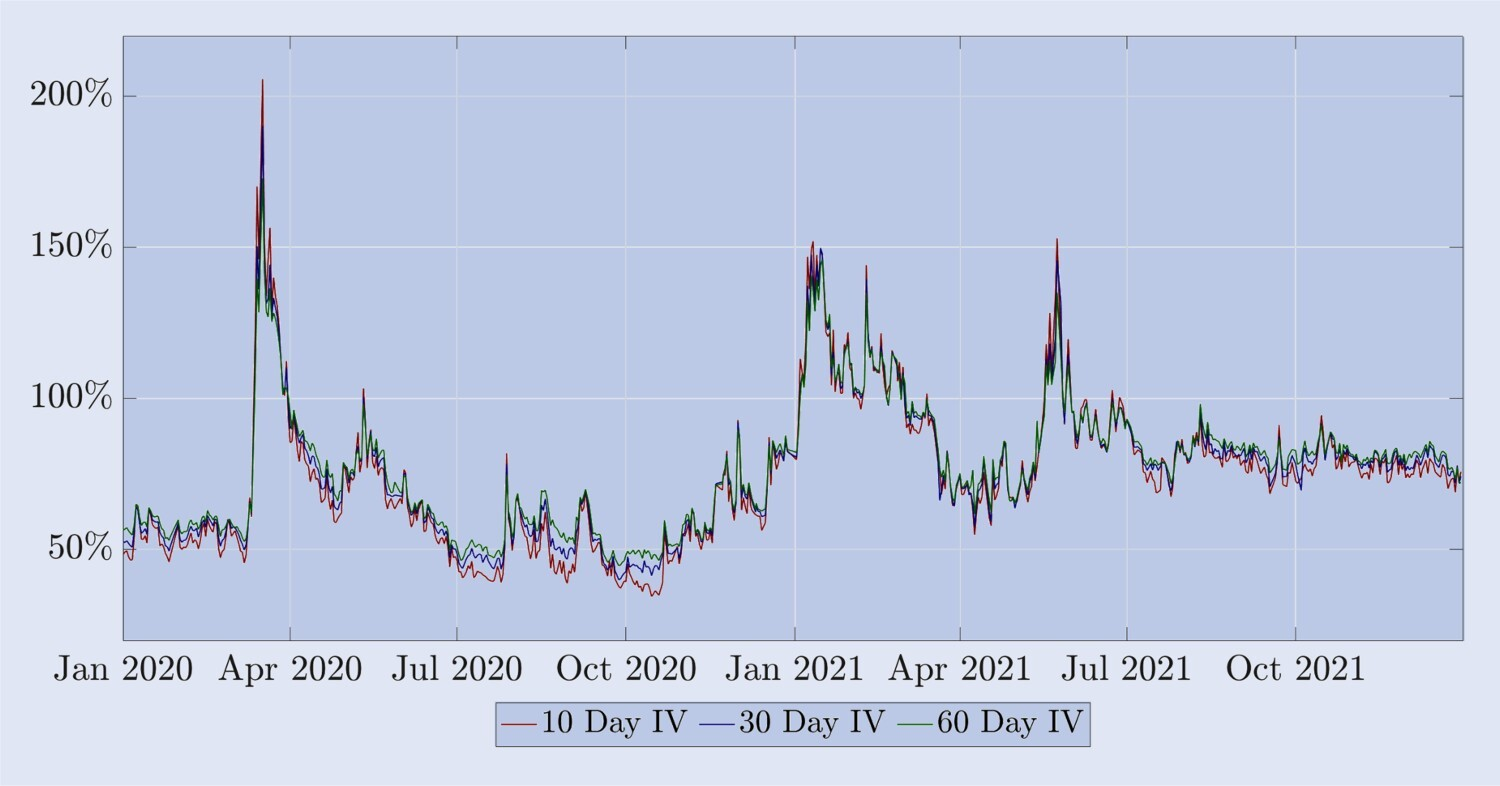
Sin embargo, algunas características son similares a las de la volatilidad implícita de las opciones sobre índices bursátiles: (i) la volatilidad de diferentes virtualidades está altamente correlacionada con la volatilidad en el dinero del mismo vencimiento, como se muestra en la Figura 3; (ii) la La volatilidad implícita de Bitcoin es La estructura temporal de volatilidad muestra fluctuaciones regulares entre futuros inversos de alta volatilidad y futuros a plazo relativamente tranquilos. La Figura 4 muestra que, de manera similar a la estructura temporal de volatilidad de los índices bursátiles, la volatilidad implícita de Bitcoin tiene fluctuaciones más pequeñas y tendencias similares durante la mayor parte del período de futuros inversos.

Figura 4. Estructura temporal de volatilidad implícita de Bitcoin.

La estructura temporal de volatilidad implícita de las opciones de Bitcoin, incluidas las fechas de vencimiento constantes de 10, 20 y 30 días, desde el 1 de enero de 2020 hasta el 31 de diciembre de 2021, calculada en función de las opciones at-the-money. Durante períodos de relativa calma, la estructura temporal muestra futuros positivos, mientras que durante las crisis (particularmente en marzo de 2020 y junio de 2021) ocurre lo contrario.

Comenzaremos el resto de este artículo utilizando las características de las opciones y futuros de Bitcoin que destacamos anteriormente. Un tenedor de Bitcoin a largo plazo podría comprar una opción de venta fuera del dinero para protegerse contra una caída significativa del precio y considerar cubrir la posición al contado adecuadamente. Sin embargo, los creadores de mercado y otros operadores profesionales participan activamente en la cobertura delta dinámica porque cubrir el riesgo de las opciones es fundamental para ellos como proveedores de liquidez. Podrían usar BS Delta para lograr esta cobertura, pero dada la prevalencia del ajuste Smile Curve Delta entre los operadores de opciones sobre acciones, sería interesante examinar la efectividad de este Delta para las opciones de Bitcoin. Hemos revisado la literatura que analiza la efectividad del delta ajustado por curva sonriente para cubrir opciones sobre índices de acciones y hemos demostrado que en muchos casos el delta de BS es tan efectivo como cualquier delta ajustado por curva sonriente. Sin embargo, ninguna investigación previa ha explorado esta cuestión para las opciones de Bitcoin, y está claro, a partir del comportamiento muy diferente de la curva de volatilidad implícita de Bitcoin que acabamos de discutir y la variedad de nuevos instrumentos de cobertura disponibles para Bitcoin, que no podemos simplemente extrapolar Lo que se sabe sobre las opciones sobre índices bursátiles para sacar conclusiones sobre la cobertura de las opciones de Bitcoin. Por lo tanto, el propósito de este estudio es presentar y comparar varios deltas ajustados de curva sonriente comúnmente utilizados por los profesionales para analizar su eficacia en la minimización de la desviación estándar de los errores de cobertura en las opciones de Bitcoin basadas en diferentes opciones de instrumentos de cobertura. De hecho, esta investigación podría incluso extenderse al nivel bursátil donde se llevan a cabo operaciones de negociación y/o cobertura de opciones. Por ejemplo, ¿es mejor utilizar futuros o contratos perpetuos de Binance o Deribit para cubrir opciones que cotizan en el intercambio Deribit? Pero no analizamos este nivel detallado del problema de cobertura de opciones de Bitcoin en este estudio. Al menos actualmente, al momento de escribir este artículo, el mercado de opciones de Deribit representa más del 90% de todo el volumen de opciones de Bitcoin, y las comunicaciones personales con los creadores del mercado de opciones de Deribit indican que solo utilizan la plataforma de futuros de Deribit para actividades de cobertura delta.

4. Coeficiente de cobertura

En nuestro diseño experimental, escribimos una opción europea estándar sobre futuros del índice Bitcoin por un valor de un Bitcoin y la cubrimos tomando una posición larga en una cierta cantidad de contratos de futuros. Los futuros con vencimiento en T permiten a los operadores celebrar un acuerdo para comprar o vender una cierta cantidad de Bitcoin en un momento futuro T a un tipo de cambio Bitcoin-USD acordado ahora. El activo subyacente para futuros y opciones es el Deribit Bitcoin Index BTC, que es un índice compuesto no negociable. Sin embargo, también podemos cubrir las opciones de vencimiento T con una posición de contrato perpetuo en lugar de un contrato de futuros de vencimiento T. Podemos omitir el tiempo de ejecución t en nuestra notación sin causar confusión, y denotamos el precio en el momento t de una opción inversa con un precio de ejercicio K y fecha de vencimiento T como f(K,T|F,σ), donde F es El precio perpetuo o precio de futuros con vencimiento en T, el tiempo es t, σ:=σt(K,T|F) representa la volatilidad implícita de la opción, que también es la volatilidad en el tiempo t. Al incorporar la relación entre la volatilidad y el activo subyacente en nuestro marco de cobertura, pretendemos lograr un delta más preciso que el delta de BS, es decir, el delta δadj ajustado por smile basado en la regla de la cadena.

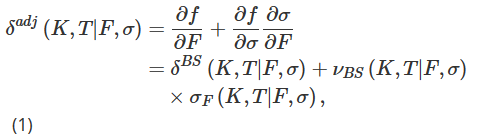
Donde δBS es el delta estándar de BS, νBS es la sensibilidad a la volatilidad del precio de la opción BS (vega) y σF = ∂σ/∂F es la sensibilidad de la volatilidad al precio, es decir, el cambio en la volatilidad implícita ante cambios en el activo subyacente… Aunque BS delta y vega tienen fórmulas de forma cerrada y son fáciles de calcular, la cuantificación de σF es relativamente difícil y existen muchos métodos diferentes.

El primer ajuste al delta de BS que analizamos tiene sus raíces en diferentes formas de parametrizar la volatilidad local de manera diferente dependiendo del estado actual del mercado o el “régimen de mercado”. El concepto de volatilidad local se ha desarrollado en una amplia gama de literatura académica, comenzando con los artículos clásicos de Dupire (1994) y Derman et al. (1996). De particular interés aquí es el “modelo pegajoso”, defendido por Derman (1999) en el contexto de la cobertura de opciones sobre índices bursátiles, que aplica diferentes parametrizaciones de volatilidad local en los nodos de un árbol binario que modela la evolución del precio del activo subyacente. Derman et al. (1996) propusieron aproximar σF como la pendiente de la volatilidad implícita con respecto al precio de ejercicio: Nota 13

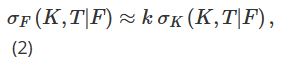
Entre ellos, σK=∂σ/∂K representa la derivada de la volatilidad con respecto al precio de ejercicio, y k debe depender del mecanismo de mercado actual. De hecho, Derman (1999) introdujo tres “modelos de rigidez” diferentes para representar el comportamiento de la volatilidad local bajo diferentes regímenes de mercado. El modelo Sticky Strike (SS) describe una situación de mercado en tendencia y supone que la volatilidad es independiente de los movimientos futuros de precios del activo subyacente y, al igual que el supuesto BS, es constante y la misma para cada opción. En este mecanismo, delta es igual a delta BS. Nota 14 El modelo Sticky Money (SM) (a veces también llamado Sticky Delta) considera un mercado con límites en el rango. Bajo este mecanismo, la volatilidad de una opción depende únicamente de su valor monetario (o equivalentemente, su delta). Por lo tanto, la volatilidad local es la misma en cada nodo del árbol, pero cada opción tiene un árbol diferente con diferente volatilidad local, dependiendo del valor monetario de la opción. A medida que cambia el precio del activo subyacente, cambia el valor monetario de la opción y tenemos que pasar a un árbol diferente para fijar el precio de la opción. Finalmente, el modelo Sticky Tree (ST) captura el comportamiento de la volatilidad local durante caídas rápidas del mercado, es decir, describe un ajuste de curva sonriente cuando existe una fuerte correlación negativa entre la volatilidad y el precio del activo subyacente. El nombre de este modelo de árbol oculto proviene del modelo de volatilidad local propuesto por Derman y Kani (1994). Del mismo modo, la volatilidad local es una función determinista, pero puede ser diferente en cada nodo del árbol, y el mismo árbol se utiliza para fijar el precio de todas las opciones. En estos tres tipos diferentes de parametrización de volatilidad local, el valor de k en la fórmula (2) será diferente dependiendo del mecanismo del mercado, como se muestra a continuación:

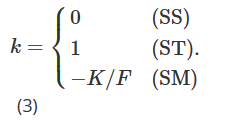
Crépey (2004) y Alexander et al. (2012) ampliaron la aproximación (2) para incluir la dependencia del estado de k. Nótese también que al combinar las ecuaciones (1) y (2) de Alexander et al. (2012) con la ecuación (3) de Alexander y Nogueira (2007b) y realizar alguna manipulación algebraica, se puede encontrar que la curva de sonrisa de Bates ( 2005) es implícitamente La delta invariante de escala (generalizada en Alexander y Nogueira (2007a)) es idéntica a la aproximación de dinero pegajoso (SM).

Dada la alta volatilidad de Bitcoin, el rango de precios de ejercicio disponibles puede variar significativamente con el tiempo. Por lo tanto, para proporcionar un marco para estudiar opciones con las mismas características durante un período de tiempo más largo, pasamos de los precios de ejercicio a los indicadores in-the-money. Definimos la monetización m como m=K/F, y ahora usamos θ(m,T|F)=σ(mK,T|F) para representar la volatilidad implícita. Denotando las derivadas parciales de θ(m,T|F) con respecto a F y m como θF(m,T|F) y θm(m,T|F) respectivamente, podemos reescribir el delta ajustado (7) como:

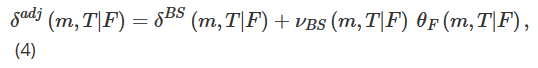
Utilizamos la hipótesis de volatilidad local propuesta por Derman (1999) para estimar la sensibilidad volatilidad-precio θF. La estructura de árbol utilizada para simular la evolución del precio de la opción variará dependiendo de los tres modelos de mercado posibles: Mercado de Tendencia Estable (SS), Mercado de Rango (SM) y Mercado de Caída con Salto (ST). Por lo tanto, al convertir el delta pegajoso de Derman (1999) en una medida monetaria, el valor de κ en (5) debería ser diferente dependiendo del modelo de mercado.

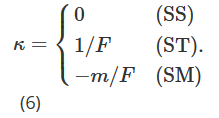
Al igual que antes, el modelo libre, sonrisa implícita, delta invariante a la escala propuesto por Bates (2005) y Alexander y Nogueira (2007a) es idéntico al delta de medida de dinero rígido (SM) de Derman y Kani (1994).

A continuación, consideramos la varianza mínima (MV) Delta δmv, es decir, la Delta que minimiza la varianza instantánea de la cartera de cobertura Delta. Aquí seguimos una aproximación introducida por Bakshi et al. (1997) que minimiza la varianza local. Lee (2001) muestra que este ajuste en el ratio de cobertura MV es de la misma magnitud que el Delta implícito de Smile (SM), pero de signo opuesto, es decir:

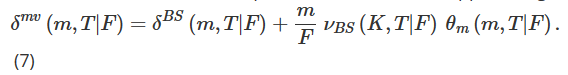
Como se explica en detalle en el Capítulo 4 de Alexander (2008), y también en otros textos sobre volatilidad implícita, la delta implícita de la sonrisa crea una dinámica contraintuitiva de “sonrisa flotante” que también significa que cuando la volatilidad Cuando la correlación tasa-precio es grande y negativo (es decir, hay un sesgo negativo significativo), el rendimiento de cobertura producido por el ajuste de SM es significativamente peor que el delta de BS. Dado que el ajuste MV tiene un signo opuesto al ajuste SM, se debería preferir MV Delta sobre BS Delta al momento de cubrir opciones sobre índices de acciones y cualquier opción con una curva de volatilidad implícita que tenga una pendiente negativa significativa.

Nuestro ajuste final de la curva de sonrisa Delta, denotado δhw, es propuesto por Hull y White (2017). Se obtiene estimando empíricamente la relación cuadrática entre el valor absoluto del PnL diario ΔP de la cartera de cobertura BS Delta y el BS Delta. Eso es:

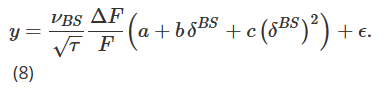
donde ΔF es el PnL diario de los futuros. Después de obtener estimaciones de parámetros (aˆ, bˆ, cˆ) utilizando datos históricos, el Delta de Hull y White (HW) se calcula de la siguiente manera:

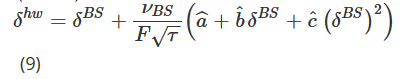
donde δBS y νBS representan el Delta y vega clásicos de BS. El precio subyacente actual se denota como F, su cambio se denota como ΔF y τ representa el tiempo de vencimiento de la opción. Los autores calculan estimaciones (aˆ, bˆ, cˆ) utilizando una ventana móvil de 36 meses y luego analizan el desempeño de la cobertura HW Delta para minimizar la desviación estándar del error de cobertura diario durante un período de 11 años a partir de enero de 2014. S&P 500 y otras opciones sobre índices bursátiles. Descubrieron que el uso de HW Delta podría mejorar el rendimiento hasta en un 26%. Otras conclusiones se basan únicamente en opciones sobre índices bursátiles y sostienen que HW Delta supera a las opciones de venta en comparación con las opciones de compra y supera a las opciones dentro del dinero en comparación con las opciones fuera del dinero. Además, afirman que HW Delta supera a muchos otros deltas derivados de varios modelos de volatilidad estocástica y volatilidad local al cubrir opciones sobre índices de acciones.

Esta sección cubre una serie de ajustes simples a BS Delta que han demostrado su eficacia en investigaciones anteriores sobre cobertura de opciones sobre índices de acciones y otras clases de activos tradicionales. La pregunta ahora es si también pueden superar la simple cobertura Delta de BS en el mercado de opciones de Bitcoin. El mercado de opciones de Bitcoin es menos maduro que los mercados de opciones tradicionales, y su volatilidad y presión de compra direccional son más significativas, y los creadores de mercado reequilibran sus inventarios basándose en la información de estas presiones. Resumimos los ratios de cobertura delta ajustados por BS considerados en este estudio en la siguiente fórmula única:

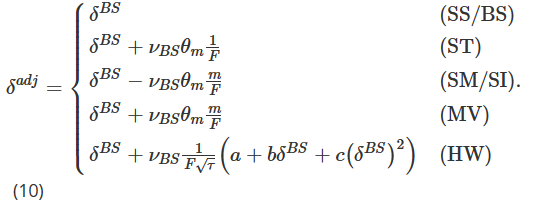
A continuación explicamos el contenido anterior:

1. Cuando m = 1, es decir, en una opción at-the-money, el ajuste MV es el mismo que el ajuste ST; de lo contrario, cuando m > 1, es decir, en una opción call out-of-the-money, el tamaño del ajuste MV es mayor que el ajuste ST; cuando m, es decir, en una opción put fuera del dinero, el tamaño del ajuste MV es menor que el ajuste ST;

2. El ajuste MV es siempre igual en tamaño y opuesto en dirección al ajuste SM, y el Delta SM es también el Delta invariante de escala (SI) libre de modelo de Alexander y Nogueira (2007a), es decir, el Delta de cualquier tipo de proceso de salto de volatilidad estocástica en los precios de las opciones de Bitcoin;

3. Los signos de los ajustes ST, SM y MV dependen de la pendiente de la curva de volatilidad implícita, θm. Cuando tiene una pendiente negativa, MV y ST Delta son menores que BS/SS Delta, mientras que SM/SI Delta es mayor que BS/SS Delta. Cuando tiene una pendiente positiva, MV y ST Delta son mayores que BS/SS Delta, mientras que SM/SI Delta es menor que BS/SS Delta.

5. Datos

Creamos una base de datos única tomando instantáneas cada hora de los datos del mercado de opciones de Deribit durante un período de varios años utilizando la API de intercambio. Estos datos contienen la información de la cartera de órdenes de nivel 1 para todas las opciones, futuros y contratos perpetuos. En este artículo, utilizamos únicamente datos con frecuencias diarias y de ocho horas, que cubren un período de dos años desde el 1 de enero de 2020 hasta el 1 de enero de 2022.

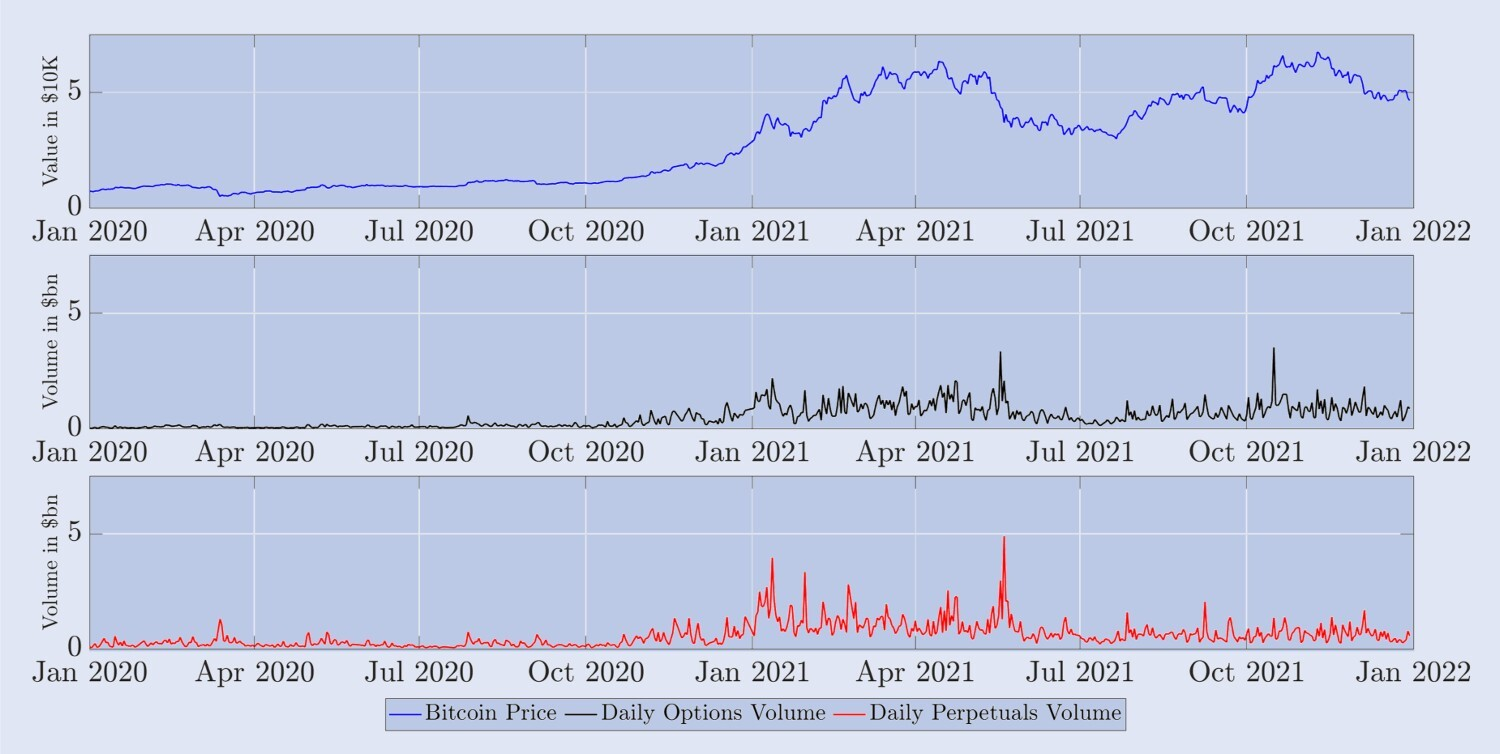
La Figura 5 muestra el precio de liquidación diario del índice BTC (es decir, el precio a las 00:00 UTC) y el volumen total de todas las opciones y contratos perpetuos negociados en Deribit durante las últimas 24 horas (en montos nocionales, en miles de millones de USD). . Los contratos de futuros no se incluyen aquí porque sus volúmenes de negociación son mucho menores que los de los contratos perpetuos y las opciones, como se muestra en la Figura 1. Durante 2020, el índice BTC subió relativamente lentamente desde niveles alrededor de \(7,000 hasta la primera gran corrida alcista que comenzó en noviembre de 2020, y el valor del índice alcanzó casi \)28,000 a fines de 2020. En 2021, el índice BTC se duplicó desde enero (alrededor de \( 28,000) hasta mediados de abril de 2021 (alrededor de \) 59,000), y luego cayó casi un 50% hasta volver a caer a \( 30,000 a mediados de julio. Alcanzó un máximo histórico de alrededor de \) 69,000 el 8 de noviembre de 2021. El panel central de la Figura 5 muestra que durante 2020, el volumen total de operaciones de 24 horas de todas las opciones en Deribit fue relativamente bajo, apenas superando los $500 millones. Sin embargo, en 2021, ha habido mercados claramente volátiles o con tendencia, con volúmenes de opciones diarias que alcanzaron los 3 mil millones de dólares comunes. El número de contratos de opciones diferentes negociados también casi se duplicó, pasando de 4,3 millones en enero de 2021 a 6,2 millones a finales de año. El gráfico a continuación muestra el volumen diario de negociación de contratos perpetuos, que registraron una mayor actividad comercial en 2021, especialmente en la primera mitad del año. Curiosamente, el crecimiento del comercio de contratos perpetuos fue más débil que el de opciones en la segunda mitad de 2021. Es probable que esto último se deba a la introducción de una serie de nuevos contratos a finales de 2020 y principios de 2021, que los operadores adoptaron gradualmente para la cobertura de gamma y vega. Esto puede haber aliviado la presión sobre la cobertura delta dinámica extremadamente activa en la segunda mitad de 2021. De hecho, como muestra la Figura 1, los volúmenes de negociación de contratos de futuros también cayeron en los últimos seis meses de 2021, incluso más que los contratos perpetuos. De todos modos, descubrir que los patrones comerciales en 2020 y 2021 eran tan diferentes motivó nuestra decisión de dividir la muestra en dos períodos de un año.

Figura 5. Evolución del índice BTC y volumen diario de negociación de derivados.

El gráfico anterior muestra el precio del índice BTC a las 00:00 UTC diariamente para un período de muestra de dos años a partir del 1 de enero de 2020 (arriba, gráfico azul); el volumen total correspondiente de 24 horas de todas las opciones en Deribit (centro, gráfico negro). gráfico); y el volumen diario de negociación de contratos perpetuos (gráfico inferior rojo). El valor del índice BTC está en unidades de $10,000 y el volumen de operaciones está en miles de millones de dólares.

Alexander et al. (2022b) documentan muchas diferencias entre los mercados de opciones de Bitcoin y S&P 500. Una de las principales diferencias es la proporción de opciones cortas, medianas y largas negociadas. Las opciones a un mes del S&P 500 son relativamente a corto plazo, ya que la mayoría de las transacciones se realizan entre el vencimiento de uno y tres meses. Sin embargo, una opción de Bitcoin con una fecha de vencimiento de un mes cae en la categoría de largo plazo. Para poner es