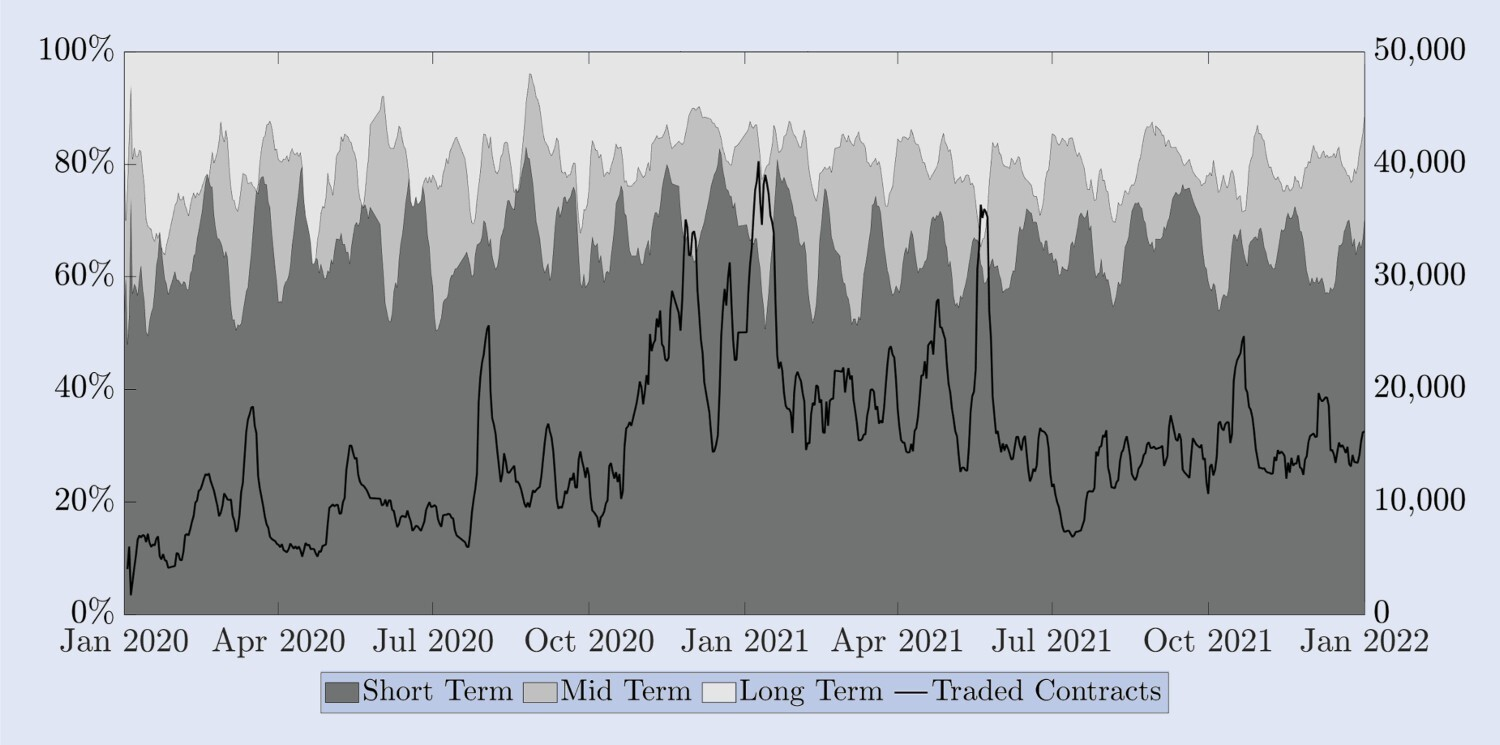
to en perspectiva, la Figura 6 muestra la proporción de contratos negociados por tiempo de vencimiento en Deribit. La línea sólida en la escala derecha representa el número de transacciones de todos los contratos que vencen. Para mayor claridad, presentamos estos datos utilizando promedios semanales durante un período móvil. El patrón estacional en la proporción de opciones de corto plazo (hasta dos semanas) es resultado de la política de programación de emisiones, que es que a menos que haya una opción mensual o trimestral estándar que venza en esa semana (o dos semanas), una opción Se emitirán las opciones correspondientes a la semana actual (o dos semanas). Las opciones con fecha de vencimiento de una semana (y/o dos semanas) En la escala de la izquierda, presentamos la proporción de vencimientos a corto plazo (hasta dos semanas), mediano plazo (entre dos semanas y un mes) y largo plazo (más de un mes). Para ello, agregamos todos los contratos negociados diariamente dentro de cada categoría de vencimiento y los presentamos como un porcentaje de todos los contratos negociados, utilizando nuevamente un promedio semanal de ventana móvil para mayor claridad. Aparte de este patrón estacional, durante todo el período de dos años, solo entre el 15% y el 20% de las transacciones se realizaron en opciones con fechas de vencimiento superiores a un mes. A pesar del creciente número de contratos negociados en nuestra muestra, la proporción de contratos con fechas de vencimiento de más de un mes se ha mantenido relativamente estable, al igual que la proporción de opciones a corto plazo que vencen dentro de dos semanas. De hecho, aproximadamente el 60% de todos los contratos negociados tienen períodos de vencimiento muy cortos. Entre el 20% y el 25% de los contratos negociados corresponden a opciones de “medio plazo” con plazos de vencimiento comprendidos entre dos semanas y un mes. Dado que las opciones con un período de vencimiento de un mes representan entre el 80 y el 85 % de todo el volumen comercial en Deribit, decidimos centrar nuestra investigación de cobertura en estas opciones. Las opciones con vencimientos superiores a un mes presentan demasiados precios obsoletos como para ser útiles en nuestro análisis empírico incluso en frecuencias horarias. Esto nos lleva a considerar una opción en cada una de las categorías de vencimiento documentadas anteriormente. Para facilitar la comparación, seleccionamos opciones de vencimiento constante de 10, 20 y 30 días como nuestros objetos de investigación, cada una de las cuales es un representante de las tres categorías principales de vencimiento.

Fig. 6. Fecha de vencimiento de las opciones negociadas.

La escala de la izquierda muestra la proporción de opciones a corto plazo (hasta dos semanas, gris oscuro), opciones a mediano plazo (entre dos semanas y un mes, gris medio) y opciones a largo plazo (más de un mes, gris claro) en el volumen total de operaciones. La línea negra (escala derecha) representa el número total de contratos de opciones negociados. Todas las series son promedios móviles semanales de datos diarios.

A continuación analizamos el filtrado de datos. Incluso si nos centramos solo en opciones con una fecha de vencimiento de un mes, aún necesitamos filtrar algunos precios obsoletos, es decir, precios de opciones que han tenido un volumen de negociación cero en las últimas 24 horas. La liquidez también es una cuestión clave para los datos sobre contratos de futuros con vencimiento limitado, ya que los precios de futuros obsoletos pueden causar errores en el cálculo del delta de la opción. Por lo tanto, preferimos utilizar la relación de paridad call-put (PCP) para inferir el precio de futuros correcto en lugar de utilizar el precio de mercado como lo hacemos para los contratos perpetuos muy líquidos. Si es necesario, filtramos los precios medios de las opciones que violan la condición de no arbitraje propuesta por Fengler (2009) y derivamos la volatilidad implícita de los precios restantes. Cabe señalar que la liquidez y la actividad comercial de las opciones OTM son mucho mayores que las de las opciones ITM con el mismo precio de ejercicio, por lo que utilizamos la volatilidad implícita de las opciones de venta para calcular el caso de m, y utilizamos la volatilidad implícita de opciones de compra. La volatilidad se utiliza para calcular el caso en que m ≥ 1. Es importante señalar que la diferencia entre la volatilidad implícita de las opciones call y put en ATM es casi insignificante. Esto nos permite crear una cuadrícula sin procesar a partir de la superficie de volatilidad implícita del mercado y luego interpolar para obtener precios filtrados como se describe a continuación.

Para obtener una serie histórica continua del precio de cada opción, construimos los precios de contratos sintéticos de vencimiento constante con fecha de vencimiento y propiedades monetarias dadas. Las opciones de corto plazo están representadas por una fecha de vencimiento fija de 10 días, las de mediano plazo son de 20 días, mientras que para el largo plazo consideramos una fecha de vencimiento de 30 días. Teniendo en cuenta que los precios de Bitcoin a menudo experimentan cambios de tendencia, es imposible comparar el mismo precio de ejercicio durante un largo período de tiempo, por lo que también seleccionamos un rango apropiado de propiedades monetarias para la interpolación. Encontramos un amplio volumen dentro de un rango de precio de ejercicio de aproximadamente un 30% por encima y por debajo de los niveles de Bitcoin. Por lo tanto, interpolamos los precios de las opciones sintéticas para cada vencimiento constante y propiedad monetaria m∈{0,7,0,8,0,9,1,1,1,1,2,1,3} Nota 15. De hecho, utilizamos el método de interpolación en la superficie de volatilidad implícita bajo el límite de no arbitraje propuesto por Fengler (2009), que también propone un método de interpolación de spline cúbico natural para suavizar la superficie de volatilidad implícita. Sin embargo, la forma de la curva de volatilidad implícita para Bitcoin varía mucho más que para otros tipos de opciones, y encontramos que la interpolación de spline cúbico es demasiado flexible y sensible a grandes intervalos entre ciertos precios de ejercicio. Por lo tanto, utilizamos polinomios de Hermite cúbicos por partes que preservan la forma para interpolar la superficie de volatilidad implícita y verificamos el precio después para asegurarnos de que no se viole la restricción de no arbitraje de convexidad con respecto al precio de ejercicio. Esta técnica se ha aplicado en muchos otros estudios académicos, como Malz (1997) y Bliss y Panigirtzoglou (2002).

En primer lugar, interpolamos la curva de sonrisa de volatilidad implícita para obtener una volatilidad implícita de monetización constante bajo la restricción de no arbitraje propuesta por Fengler (2009) utilizando polinomios de Hermite cúbicos por partes que preservan la forma. A continuación, obtenemos la volatilidad implícita de las opciones de dinero constante y vencimiento constante interpolando la estructura temporal de volatilidad y utilizamos esta volatilidad implícita para crear precios de opciones sintéticas Nota 16. Para evitar cualquier posibilidad de arbitraje de calendario, nos aseguramos de que la variación implícita total aumente con la fecha de vencimiento. Para evaluar el rendimiento de la cobertura, también necesitamos registrar el precio de cada opción sintética dentro de un incremento de tiempo sin cambiar el straddle utilizado para construir la opción correspondiente. Sólo este marco nos permite registrar las ganancias y pérdidas de una cartera de cobertura dinámica. Por lo tanto, creamos futuros y opciones sintéticos utilizando los métodos que acabamos de describir para obtener valores monetarios y precios de opciones actualizados con fechas de vencimiento de 9, 19 y 29 días para el conjunto de datos diarios. De manera similar, en el conjunto de datos de 8 horas, construimos futuros y opciones con fechas de vencimiento 8 horas menores a 10, 20 y 30 días. En total, generamos aproximadamente 175.000 precios de opciones sintéticas con frecuencia diaria y 88.000 ratios de cobertura, y más de 525.000 precios de opciones sintéticas con frecuencia de 8 horas y más de 263.000 ratios de cobertura.

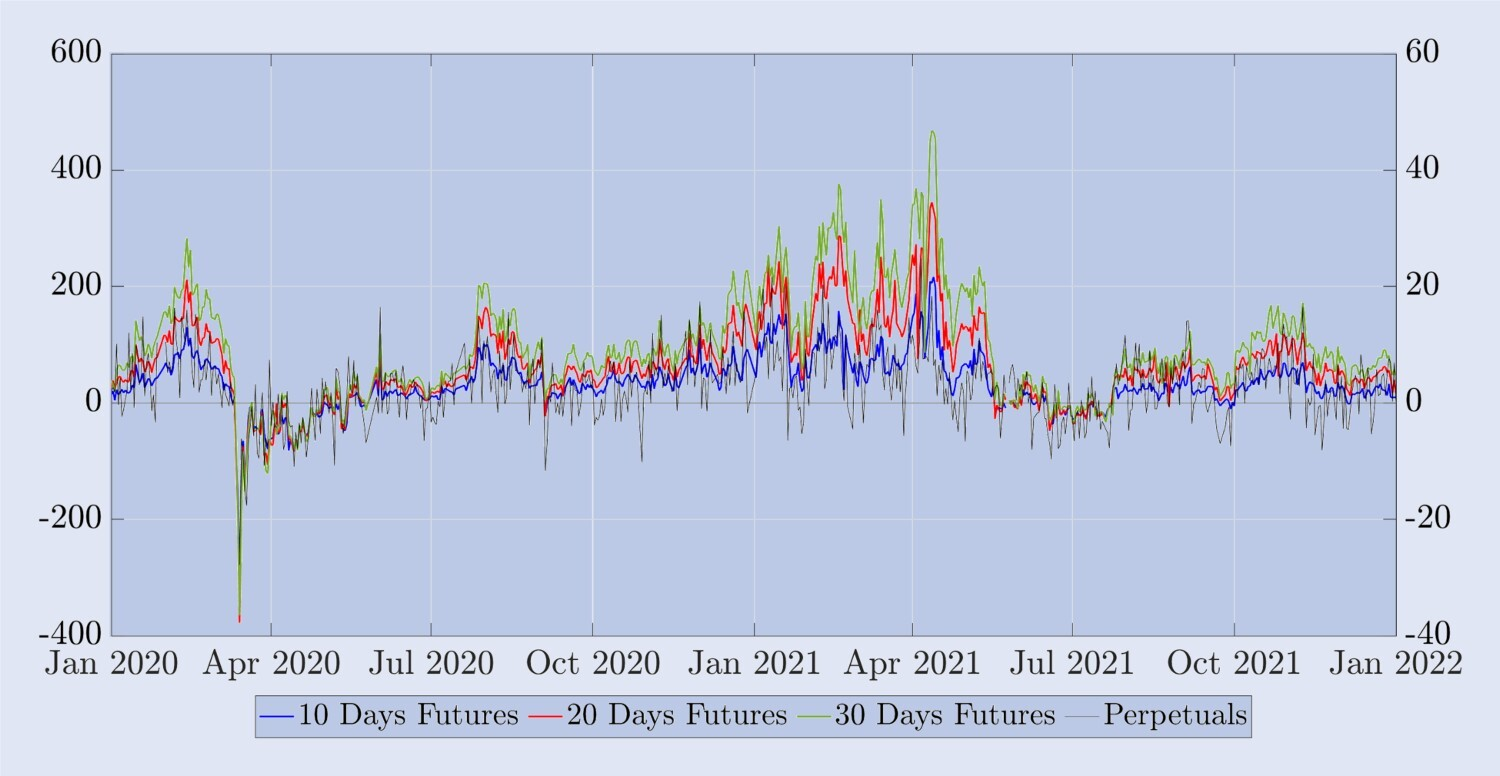
A continuación, examinaremos algunas características empíricas de los contratos perpetuos de Bitcoin y los compararemos con los futuros con vencimiento fijo antes de pasar a nuestro estudio de cobertura. El precio de liquidación de las opciones de Bitcoin no es un contrato negociable, por lo que necesitamos utilizar futuros o contratos perpetuos como herramientas de cobertura. En este caso, la eficacia de utilizar contratos de futuros para cubrir opciones depende de factores como la variabilidad de la base. Para ilustrar esta variabilidad, la Figura 7 muestra la diferencia entre el precio del mercado de futuros (o contrato perpetuo) y el índice BTC, dividido por el índice BTC. Esta base porcentual se expresa en puntos básicos (pb), siendo la escala de la izquierda la de los tres futuros sintéticos con vencimiento fijo y la escala de la derecha la base relativa al contrato perpetuo. Debido al mecanismo de tasa de financiamiento, el riesgo base de los futuros perpetuos es muy bajo: menos de ±10 puntos básicos la mayor parte del tiempo. Pero también es muy volátil: por ejemplo, durante la crisis del COVID en marzo de 2020, la base perpetua alcanzó casi -150 puntos básicos. Los contratos perpetuos tienen muy poco riesgo de base, lo que sugiere que pueden proporcionar una mejor herramienta de cobertura que los futuros calendario con la misma fecha de vencimiento de la opción. A diferencia de la base perpetua, la base de los futuros con vencimiento fijo es casi siempre positiva. Para los futuros a 10 días, la base puede ser de hasta 100 puntos básicos, mientras que para los futuros a más largo plazo, la base puede incluso alcanzar los 450 puntos básicos. Además, como se puede ver en este gráfico, las curvas de futuros a 10, 20 y 30 días generalmente tienen una prima positiva; de hecho, el orden es F30>F20>F10 en 620 de los 730 días muestreados, y solo en marzo de 2020. ¿Cambia el orden? La acción opuesta ocurrió durante junio/abril (la caída de la COVID y sus consecuencias) y junio/julio de 2021 (el final de la larga racha alcista de Bitcoin).

Figura 7. Diferencias entre contratos spot, perpetuos y futuros.

El precio de futuros menos el índice BTC, dividido por el índice BTC, expresado en puntos básicos. La escala de la derecha mide el porcentaje base para futuros perpetuos (negro), y la escala de la izquierda mide el porcentaje base para futuros con fechas de vencimiento fijas de 10, 20 y 30 días (azul, rojo y verde, respectivamente). La muestra cubre un período de dos años a partir de enero de 2020, con instantáneas diarias tomadas a la medianoche UTC.

Otro factor que afecta el éxito de una estrategia de arbitraje delta dinámico son los costos de transacción. Si el diferencial entre oferta y demanda del instrumento cubierto es grande, entonces el reequilibrio frecuente del arbitraje delta (en nuestro caso, no solo diariamente sino cada 8 horas) puede erosionar el rendimiento de la cobertura. Sin embargo, para cualquier opción dada, el delta no puede variar entre valores extremadamente diferentes, por ejemplo, una opción de compra cercana al precio de mercado siempre tendrá un delta cercano a 0,5, independientemente del modelo utilizado; consulte Vähämaa (2004) para obtener más información. ejemplo. Por lo tanto, diferentes valores delta pueden tener un impacto significativo en el rendimiento de la cobertura solo cuando el diferencial entre oferta y demanda es grande. Sin embargo, los diferenciales entre oferta y demanda en los futuros perpetuos son estrechos, e incluso los diferenciales entre oferta y demanda en los futuros calendario son estrechos. En el caso de los futuros perpetuos, el diferencial entre oferta y demanda rara vez supera un mínimo de $0,50, lo que equivale a entre 0,1 y 0,25 puntos básicos, dependiendo del nivel de precios. Los futuros de calendario tienen diferenciales entre oferta y demanda ligeramente mayores y aumentan a medida que aumenta la fecha de vencimiento, pero estos diferenciales también son muy pequeños en nuestra muestra. Incluso en el caso de los contratos de futuros con vencimiento más largo, los diferenciales rara vez superan los 5 puntos básicos y rondan 1 punto básico la mayor parte del tiempo. Un spread tan bajo tiene poco impacto en nuestras comparaciones entre diferentes valores delta, por lo que lo ignoraremos en la siguiente investigación empírica.

6. Investigación empírica de cobertura

Inspirados por nuestro debate en las Secciones 2, 3 y 5, tratamos las opciones inversas como opciones FX tradicionales, es decir, utilizamos el valor actual de la opción subyacente para convertir su precio de Bitcoin en su valor correspondiente en USD. Elegimos fechas de vencimiento fijas de 10, 20 y 30 días para los precios de futuros y opciones sintéticos continuos, y el valor monetario de las opciones se elige entre 0,7 y 1,3. Nuestros datos están construidos para coberturas que se reequilibran cada 8 horas o diariamente, y la muestra abarca un período de dos años desde el 1 de enero de 2020 hasta el 1 de enero de 2022, dividido en dos períodos de un año. Muestras para mostrar los resultados. En cada momento t, vendemos una opción europea con divisa m y fecha de vencimiento T, y la cubrimos con un contrato perpetuo o un contrato de futuros con la misma fecha de vencimiento que la opción. Las ganancias y pérdidas se registran como errores de cobertura en términos físicos, en de la forma habitual (véase, por ejemplo, Hull y White (2017). La volatilidad del mercado intradiario puede ser muy grande y el reequilibrio tiene costos de transacción muy bajos, como se explicó anteriormente. Por lo tanto, establecemos la frecuencia base de la tabla de resultados en cada 8 horas. También hacemos coincidir el reequilibrio de 8 horas con los horarios de financiación del contrato perpetuo, que son las 00:00, las 08:00 y las 16:00 UTC. Esto se debe a que el reequilibrio mediante contratos perpetuos de cobertura también puede utilizarse para obtener ganancias a partir de sus pagos de financiación. Nota 17

A excepción del delta HW, todos los deltas en (10) requieren que calculemos la pendiente de la curva de volatilidad implícita al reequilibrar la cartera de cobertura. Investigamos varias técnicas numéricas para calcular la derivada de la curva de volatilidad implícita y descubrimos que ajustar un polinomio cúbico es el enfoque más simple y preciso. Con base en los valores de pendiente que calculamos numéricamente, para cada opción, dependiendo de su valor monetario y fecha de vencimiento, aplicamos (10) para calcular el delta y vega de BS utilizando la fórmula estándar de BS. Para el delta de Hull y White (2017), no imitamos su período de calibración en la muestra de 36 meses que utilizan en su trabajo empírico sobre opciones sobre índices de acciones. Ni siquiera hay 36 meses de datos útiles disponibles para las opciones de Bitcoin. Además, los precios de Bitcoin son mucho más volátiles que el valor del S&P 500, por lo que nos gustaría considerar realizar cobertura varias veces al día. Teniendo en cuenta todos estos factores, calibramos los parámetros delta de HW utilizando 30 ventanas de observación con frecuencia diaria y 90 ventanas de observación con frecuencia de 8 horas. Nuestros resultados comparan los errores de cobertura utilizando futuros con vencimiento fijo y contratos perpetuos y ejecutan dos regresiones HW dependiendo del instrumento de cobertura.

Presentaremos nuestros resultados utilizando una prueba F estándar de diferencias de varianza, utilizando el delta BS como punto de referencia, es decir, el delta Sticky Strike (SS) de (10). En primer lugar, la Tabla 2 presenta los resultados de la cobertura de opciones a 7 días, 1 día y 3 días con grados de divisas entre 10,20 y 30,0, donde cada opción se cubre con los futuros de vencimiento fijo correspondientes y se reequilibra cada 8 horas. balance. Las entradas de la tabla son ratios de varianza, es decir, la varianza de los errores cubiertos δadj en relación con la varianza de los errores cubiertos delta BS.

Tabla 2. Resultados de cobertura de la prueba F (reequilibrio de 8 horas, futuros con fecha de vencimiento fija).

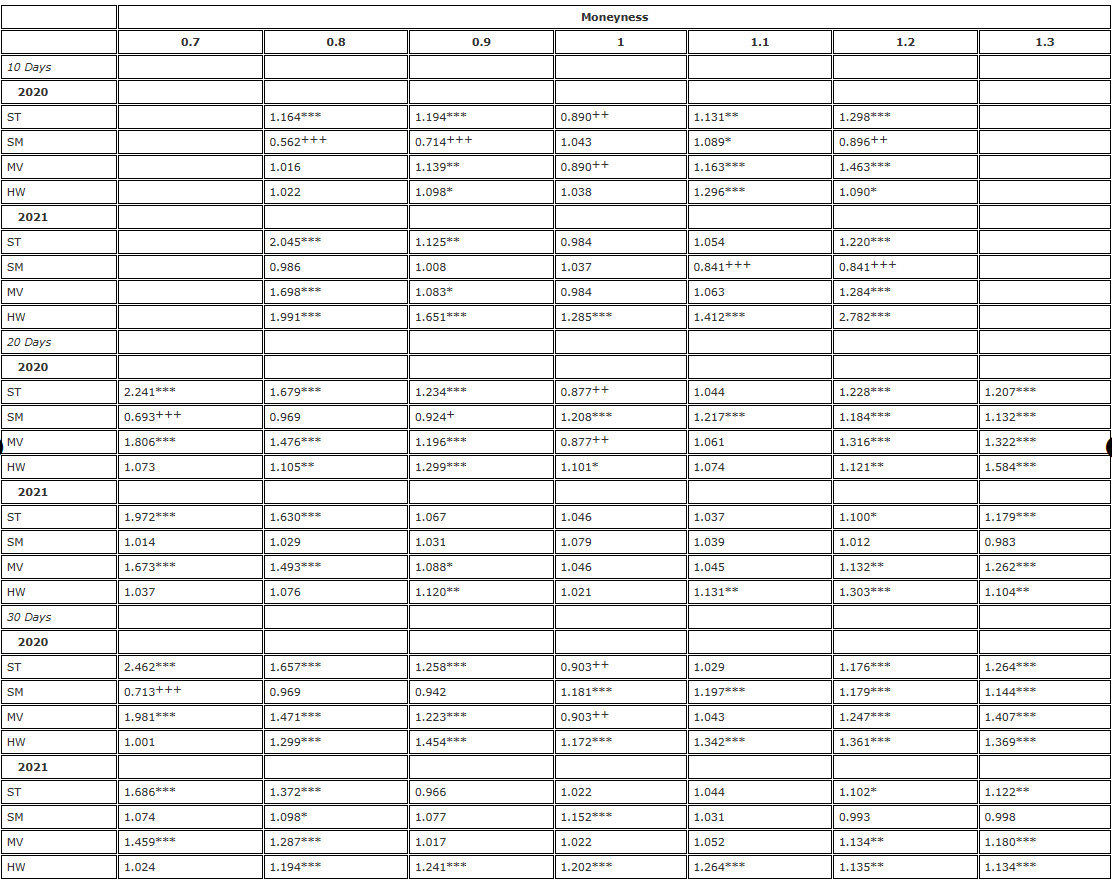
Nota: El nivel de significancia de la razón de varianza y la prueba F unilateral son para la hipótesis nula 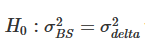y la hipótesis alternativa respectivamente. La cobertura se basa en un contrato de futuros con la misma fecha de vencimiento que la opción y se reequilibra cada 8 horas. Comparamos la varianza de los errores de diferentes coberturas delta en relación con la varianza de la cobertura utilizando BS delta y dividimos la muestra de dos años en dos partes. Utilizamos opciones de tres vencimientos diferentes con un valor monetario que iba desde 0,7 a 1,3, utilizando opciones de venta OTM cuando el valor monetario <1 y opciones de compra OTM cuando el valor monetario >1. Para H∗, , y se utilizan para representar los niveles de significancia del 10%, 5% y 1%, respectivamente, y lo mismo es válido para H+.

Cuanto mayor sea la eficacia de la cobertura, menor será la varianza del error de cobertura, y la ganancia de eficiencia al utilizar el delta de la curva de sonrisa ajustada es 1 menos esta relación de varianza. Por ejemplo, al cubrir una opción a 10 días con un valor monetario de 0,8, el delta SM (Smile Implied) produce una relación de varianza de 0,562. Esto significa que la ganancia de eficiencia en comparación con la cobertura delta BS es 1-0,562 = 43,8%, lo cual es muy significativo, por lo que esta entrada está marcada como +++. En las tablas de razones de varianza, los superíndices indican la significancia de las razones de varianza en los niveles de significancia del 10%, 5% y 1% en la prueba F unilateral. Por ejemplo,***Esto indica que la varianza del error de cobertura δadj es mayor que la del error de cobertura delta BS al nivel del 1%. Y ++ indica que la varianza del error de cobertura δadj es significativamente menor que el error de cobertura delta BS en el nivel del 5%.

Consideremos primero los resultados para 2020 en la Tabla 2. Esta parte de la muestra se caracteriza por aumentos de precios lentos pero constantes, en consonancia con el patrón de tendencia constante de Derman (1999), donde esperaríamos que el delta SS (delta BS) proporcione la cobertura delta más eficaz, o en el caso de un Patrón de distribución limitada, la mayoría de los deltas corresponden a SM delta. Dominancia. En general, los resultados de 2020 en la Tabla 2 muestran un patrón en el que el éxito de un delta particular que supera a una cobertura BS depende del valor monetario de la opción, en lugar del vencimiento. Por ejemplo, para opciones at-the-money, ST delta funciona mejor. Nota 18 Las ganancias de eficiencia logradas varían desde el 9,7% para la opción at-the-money a 30 días hasta el 12,3% para la opción a 20 días y el 11% para la opción a 10 días. La dirección del desempeño relativo de los deltas implícitos en la sonrisa (es decir, SM) en comparación con los deltas ST y MV es opuesta, no solo para las opciones at-the-money, sino también para todas las opciones in-the-money. Supera al delta de BS en la cobertura de opciones de venta OTM, pero no en las opciones de compra OTM (a excepción de la opción de compra a 10 días con un valor monetario de 1,2). Para cubrir opciones put OTM profundas de 20 días, la ganancia de eficiencia utilizando el delta implícito de Smile (SM) a lo largo de 2020 es 1-0,693 = 30,7 %, lo cual es muy significativo. Para las opciones de venta OTM de 30 días de profundidad, la ganancia de eficiencia es del 28,7%, lo que es casi lo mismo. En el caso de otras opciones de venta, las ganancias de eficiencia derivadas del uso de coberturas implícitas son mucho menores y oscilan entre el 3,1% y el 7,6%.

Sin embargo, para todas las demás opciones, todos los deltas de sonrisa ajustados tienen un rendimiento inferior al delta de BS. Sin embargo, esto no es sorprendente ya que el precio de Bitcoin ha tenido una tendencia constante durante gran parte de 2020. La relación de cobertura HW real propuesta por Hull y White (2017) y la cobertura de varianza mínima (MV) de Lee (2001) tampoco mejoran el delta de BS (excepto que para las opciones al dinero, la cobertura de MV es la misma que la de ST). cobertura). Una desventaja importante de HW delta es que utiliza regresión para estimar sus parámetros, lo que hace que el supuesto de independencia e idéntica distribución sea inválido para un activo como Bitcoin, que es muy propenso a saltos de retorno. El impacto de cualquier salto permanecerá dentro de la ventana móvil durante mucho tiempo y, por lo tanto, tendrá un gran impacto en la relación de cobertura de HW.

Las figuras 2 y 5 muestran que 2021 se ha caracterizado por precios más altos, mayor volatilidad y un aumento en los niveles generales de volatilidad, junto con una curva de volatilidad implícita en forma de sonrisa más plana, pero aún asimétrica. A lo largo de 2021, el precio de Bitcoin fluctuó enormemente entre \(30,000 y casi \)70,000, y como muestra la Figura 2, la curva de la sonrisa de 30 días se volvió relativamente plana hacia el final de este período. Pero la curva de sonrisa plana hace que el componente clave del delta ajustado, la pendiente de la curva de sonrisa, sea casi redundante. Por lo tanto, no es sorprendente que en el segundo año de nuestra muestra todos los deltas ajustados por la curva sonriente no proporcionen una mejora significativa en los ratios de cobertura BS estándar para todas las opciones a 20 y 30 días. Sin embargo, en 2021, la curva de sonrisa de muy corto plazo de 10 días exhibió algunas características extrañas, con tendencia al alza durante la fase alcista del precio de Bitcoin. Es por esto que la cobertura delta Smile Implied (SM) de opciones call out-of-the-money a 10 días muestra una mejora de eficiencia muy significativa del 15,9 % en comparación con el uso delta BS.

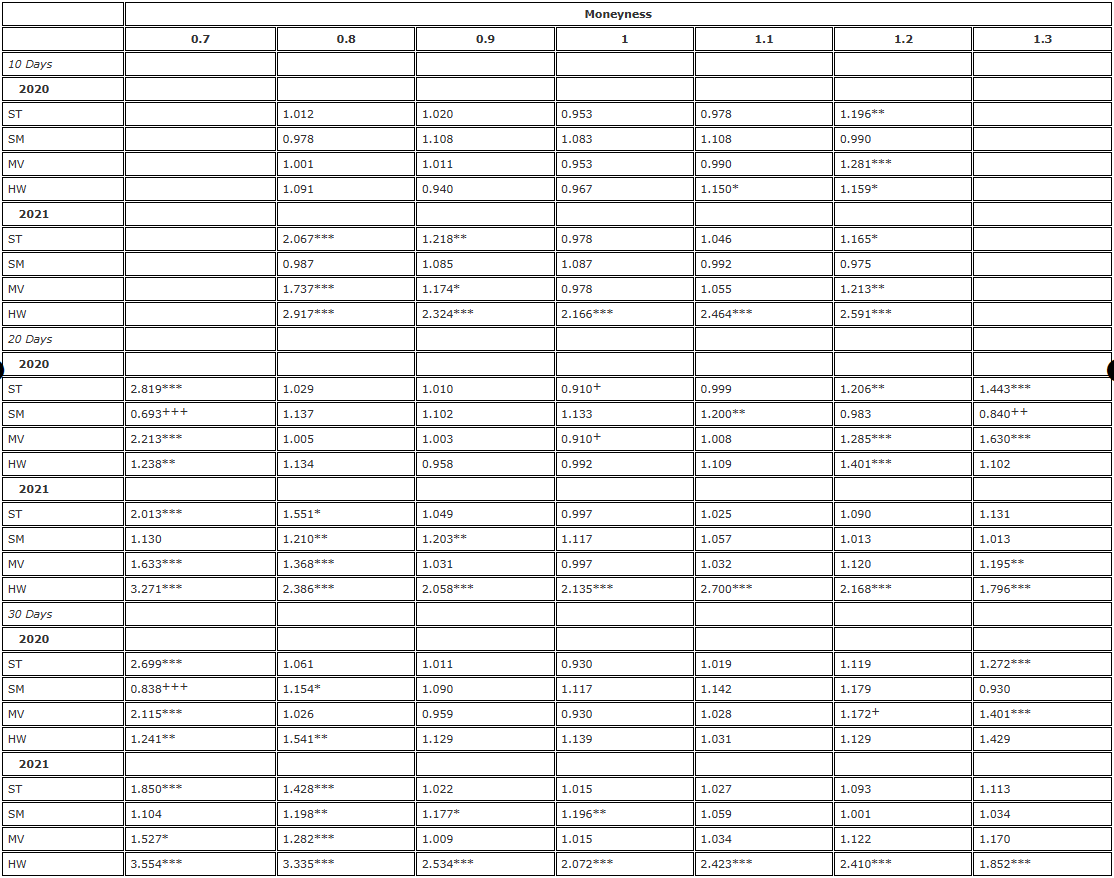
A continuación, las Tablas 3 y 4 prueban la solidez de los resultados de la Tabla 2 de dos maneras: primero, volviendo a ejecutar el análisis con una frecuencia diaria (Tabla 3) y luego, utilizando contratos perpetuos en lugar de futuros con el mismo vencimiento como instrumento de cobertura. . Los resultados de la Tabla 3 muestran un patrón similar a los de la Tabla 2, excepto que son menos significativos en general, pero esto no debería sorprendernos ya que ahora hay solo 365 en lugar de 1.095 observaciones por año. Confirman nuestra conclusión de la Tabla 2 de que ningún delta de la curva sonriente ajustada puede mejorar el delta de la escala de condición física en 2021. En 2020 también hemos visto el mismo patrón de rendimiento en relación con el delta de BS, es decir, el delta de ST superó al de BS en opciones ATM, pero ahora hay alguna evidencia de que el delta de HW supera al de BS en opciones ATM y opciones de venta OTM. También superó al de BS con un moneyness de 0,9, pero ninguna de estas estadísticas de razón de varianza fue estadísticamente significativa.

Tabla 3. Resultados de cobertura de la prueba F (reequilibrio diario, futuros con vencimiento fijo).

Nota: El nivel de significancia de la razón de varianza y la prueba F unilateral son para la hipótesis nula 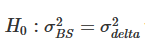y la hipótesis alternativa respectivamente. La cobertura se basa en un contrato de futuros con la misma fecha de vencimiento que la opción y se reequilibra cada 8 horas. Comparamos la varianza de los errores de diferentes coberturas delta en relación con la varianza de la cobertura utilizando BS delta y dividimos la muestra de dos años en dos partes. Utilizamos opciones de tres vencimientos diferentes con un valor monetario que iba desde 0,7 a 1,3, utilizando opciones de venta OTM cuando el valor monetario <1 y opciones de compra OTM cuando el valor monetario >1. Para H∗, , y se utilizan para representar los niveles de significancia del 10%, 5% y 1%, respectivamente, y lo mismo es válido para H+.

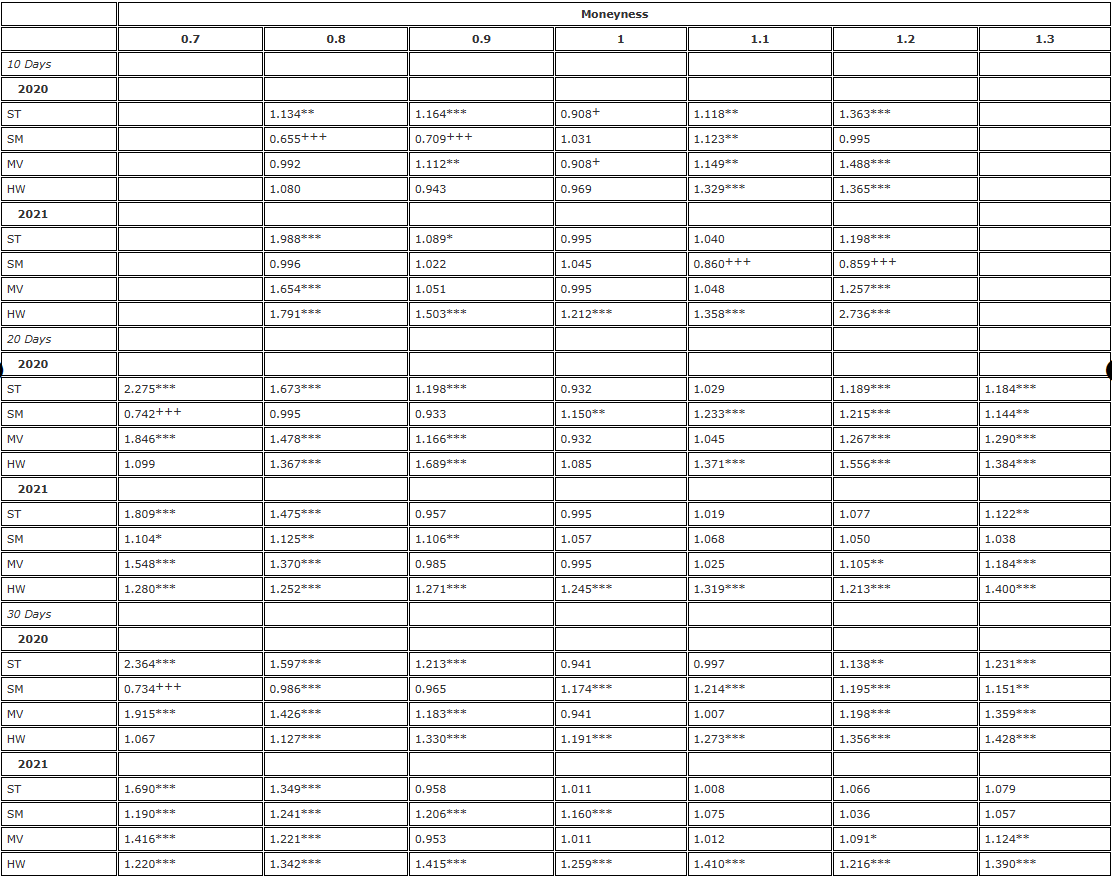
Tabla 4. Resultados de cobertura de la prueba F (reequilibrio de 8 horas, contrato perpetuo).

Nota: El nivel de significancia de la razón de varianza y la prueba F unilateral son para la hipótesis nula 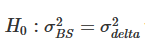y la hipótesis alternativa respectivamente. La cobertura se basa en un contrato de futuros con la misma fecha de vencimiento que la opción y se reequilibra cada 8 horas. Comparamos la varianza de los errores de diferentes coberturas delta en relación con la varianza de la cobertura utilizando BS delta y dividimos la muestra de dos años en dos partes. Utilizamos opciones de tres vencimientos diferentes con un valor monetario que iba desde 0,7 a 1,3, utilizando opciones de venta OTM cuando el valor monetario <1 y opciones de compra OTM cuando el valor monetario >1. Para H∗, , y se utilizan para representar los niveles de significancia del 10%, 5% y 1%, respectivamente, y lo mismo es válido para H+.

La Tabla 4 es exactamente la misma que la Tabla 2, utilizando una frecuencia de reequilibrio de 8 horas para el análisis, pero utilizando contratos perpetuos como instrumentos de cobertura para todas las opciones. Vemos exactamente el mismo patrón de bajo rendimiento delta de BS que en la Tabla 2, con ganancias de eficiencia muy significativas para la cobertura de opciones de venta OTM utilizando deltas ST/MV con opciones delta smile-implícitas (es decir, SM) y ATM. Con la excepción de la cobertura delta implícita (SM) de Smiling Curve, que una vez más generó una ganancia de eficiencia grande y significativa para la cobertura de opciones de compra OTM a 10 días, ningún delta ajustado de Smiling Curve pudo superar significativamente al delta de BS en 2021. En el caso de las opciones ATM, también hay algunas pequeñas ganancias de eficiencia (%) utilizando el delta ST/MV, y los índices de varianza de la Tabla 4 son casi siempre menores que los de la Tabla 2.

Este hallazgo nos lleva a preguntarnos: ¿Los contratos perpetuos ofrecen una mejor herramienta de cobertura que los futuros con el mismo vencimiento que las opciones? Para responder a esta pregunta, analizamos la relación de varianza, donde el numerador es la varianza del error de cobertura perpetua y el denominador es la varianza del error de cobertura de futuros. Nuevamente dividimos la muestra en dos períodos de un año y presentamos los resultados por delta (ahora incluyendo el delta BS) y opción, y la Tabla 5 muestra los resultados. En la tabla, una relación de varianza menor que (mayor que) 1 indica que se puede lograr un mejor (peor) efecto de cobertura utilizando contratos perpetuos. La importancia de la estadística F depende de si el swap perpetuo proporciona una herramienta de cobertura mejor (+) o peor (-) que los futuros del mismo vencimiento.*). Está claro que el resultado no depende casi nada del valor de la opción, sino más bien de la fecha de vencimiento de la opción y de las condiciones del mercado en ese momento. En el caso de las opciones a 10 días, los ratios de compra OTM son en su mayoría inferiores a 1. En el caso de las opciones a 20 y 30 días, la cobertura con opciones perpetuas podría experimentar algunas mejoras muy significativas, especialmente en 2021.

Tabla 5. Prueba F comparando futuros y swaps perpetuos (reequilibrio cada 8 horas).

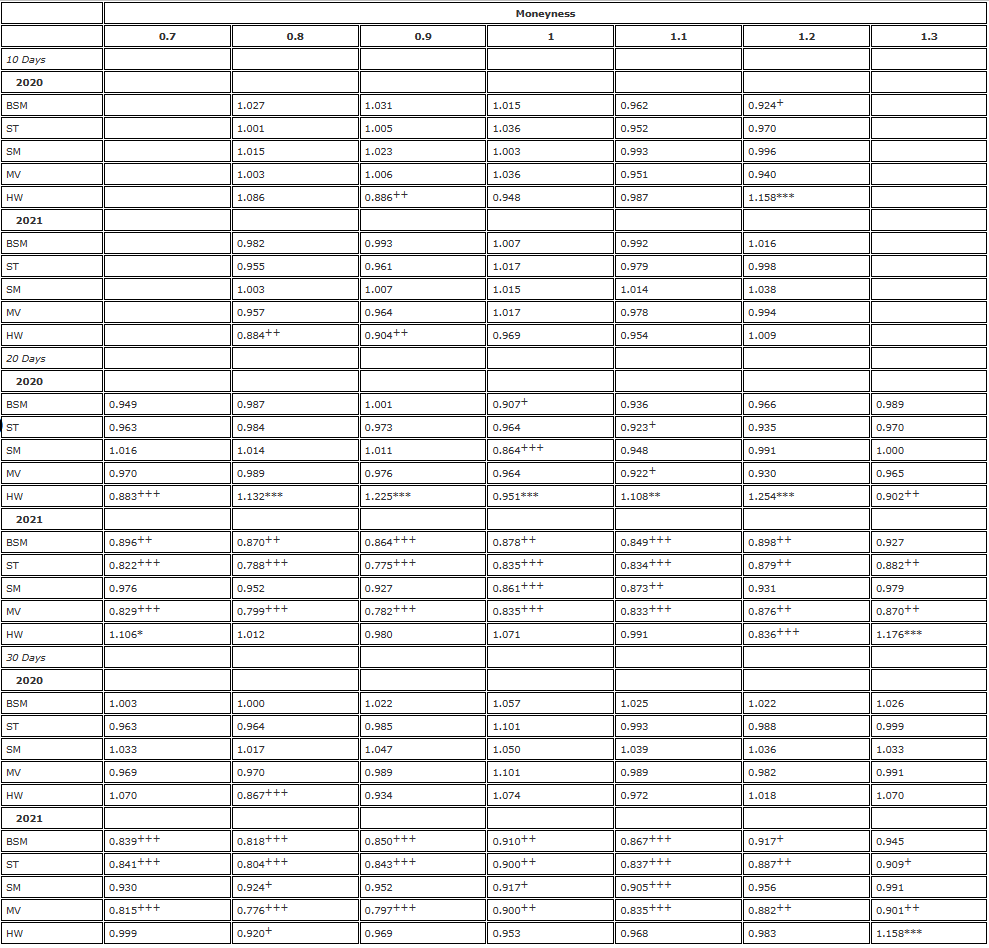
Nota: El nivel de significancia de la razón de varianza y la prueba F unilateral son para la hipótesis nula 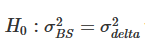y la hipótesis alternativa respectivamente. La cobertura se basa en un contrato de futuros con la misma fecha de vencimiento que la opción y se reequilibra cada 8 horas. Comparamos la varianza de los errores de diferentes coberturas delta en relación con la varianza de la cobertura utilizando BS delta y dividimos la muestra de dos años en dos partes. Utilizamos opciones de tres vencimientos diferentes con un valor monetario que iba desde 0,7 a 1,3, utilizando opciones de venta OTM cuando el valor monetario <1 y opciones de compra OTM cuando el valor monetario >1. Para H∗, , y se utilizan para representar los niveles de significancia del 10%, 5% y 1%, respectivamente, y lo mismo es válido para H+.

Si bien la tabla resultante proporciona la eficiencia relativa general del delta con respecto a diferentes ajustes de la curva sonriente, nuestra muestra de dos años cubre una amplia gama de regímenes de mercado. Como se muestra en la Figura 5, el mercado de Bitcoin fluctúa rápidamente entre tendencias estables, fluctuaciones de rango y fuertes caídas y subidas. Por lo tanto, para ayudar a entender qué delta funciona mejor en qué estados del mercado, la Figura 8 representa la serie temporal de la relación de varianza, que es la varianza del error de cobertura delta ajustado de la curva sonriente dividida por la varianza del error de cobertura delta de BS. Esto reequilibra la cobertura cada 8 horas y ahora cada varianza se calcula utilizando solo las 90 observaciones más recientes: la misma ventana utilizada para la estimación del parámetro delta de HW. Destacamos que los valores mayores a 1 indican un desempeño deficiente de la cobertura del delta ajustado por smile en relación con el delta BS. Para mayor claridad, presentamos los resultados en una escala logarítmica, por lo que en estas figuras una razón de varianza de 1 se representa como cero… Cualquier línea por debajo de cero indica que delta mejora el delta de BS, pero una línea por encima de cero muestra que delta proporciona una cobertura menos efectiva que BS.

Figura 8. Rendimiento de la cobertura de la muestra móvil. (a) resultados de opciones a 10 días y (b) resultados de opciones a 30 días.

La relación de varianza muestra el desempeño de varias relaciones de cobertura de opciones perpetuas en relación con el delta de BS utilizando un reequilibrio de 8 horas, donde la varianza del error de cobertura se calcula utilizando las primeras 90 observaciones. Presentamos los resultados logarítmicos para las opciones (a) a 10 días y (b) a 30 días en una muestra de dos años. La línea continua 0 es un valor de referencia, una relación mayor que 0 indica un peor rendimiento en relación con BS y una relación menor que 0 indica un mejor rendimiento en relación con BS. La figura (a) anterior muestra el rendimiento de una opción de venta OTM con m=0,8, mientras que el gráfico superior de (b) muestra el rendimiento de una opción de venta OTM con m=0,7. El gráfico del medio muestra el rendimiento de (a) y (b). El rendimiento de las opciones ATM se muestra a continuación para las opciones call OTM con (a) monetización de 1,2 y (b) monetización de 1,3.

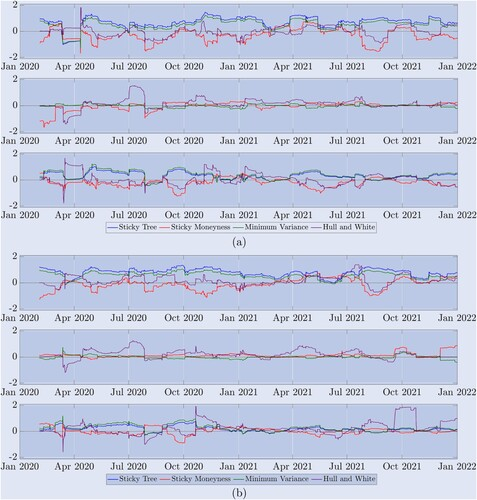
Los tres gráficos superiores (a) muestran los resultados de las opciones a 10 días, y los tres gráficos inferiores (b) muestran los resultados de las opciones a 30 días. En cada caso (a) y (b), los gráficos anteriores corresponden a opciones de venta OTM. Estos gráficos confirman los resultados de la Tabla 2: los deltas de ST (azul) y MV (verde) tuvieron un rendimiento inferior durante casi todo el período. , son inferiores que BS; según las expectativas de clasificación de mercado de Derman (1999), el delta de SM supera al delta de BS durante los períodos en los que el mercado está limitado por un rango, pero cuando el mercado está en tendencia, como el primer período que comienza en enero de 2021, durante el segundo Durante la corrida alcista y la segunda corrida alcista más tarde ese año, el delta SM no tuvo tan buen desempeño como el delta BS, mientras que el delta HW tuvo un desempeño diferente. El gráfico del medio de cada conjunto de gráficos muestra la relación de varianza de las opciones ATM cubiertas. En este caso, todos los deltas ajustados por sonrisa son muy similares, ya que la sonrisa de Bitcoin suele ser (pero no siempre) muy plana en este punto. El gráfico inferior de cada conjunto de gráficos muestra el rendimiento de diferentes deltas para cubrir opciones de compra OTM. Nuevamente, SM delta parece ser la mejor opción, pero solo está disponible para opciones a 10 días y no es una mejora tan grande respecto de BS como lo expresó OTM. En el caso de las opciones a 30 días, ningún delta ha podido mejorar consistentemente las condiciones financieras, especialmente durante 2021.

7. Conclusión

Estudios empíricos académicos previos solo han examinado la cobertura delta con una curva sonriente implícita sin modelo y una curva sonriente dependiente de la institución ajustada para opciones sobre índices bursátiles. Si bien los resultados son mixtos, la conclusión general es que un ratio de cobertura ajustado a la curva sonriente solo puede mejorar el rendimiento del delta de Black-Scholes para opciones de venta fuera del dinero en ciertas circunstancias. Pero hemos demostrado que la curva de sonrisa de volatilidad implícita de Bitcoin se comporta de manera muy diferente a las opciones sobre índices bursátiles, por lo que resulta de gran interés estudiar la eficacia de la relación de cobertura ajustada a la curva de sonrisa que los profesionales suelen favorecer.

Recomendamos el uso de diversos usos potenciales del delta ajustado, la mayoría de los cuales se basan únicamente en la relación entre la volatilidad implícita de la opción de cobertura y la pendiente de la curva de la sonrisa de volatilidad implícita en el momento del vencimiento. Al utilizar un conjunto de datos único sobre las opciones de Deribit, podemos comparar el rendimiento de cobertura de las opciones de Bitcoin más activas en el intercambio de Deribit, es decir, opciones con precios de ejercicio un 30% por encima y por debajo del índice BTC actual y tiempos de vencimiento de hasta un mes. Analizamos la varianza de los errores de cobertura delta, donde el instrumento de cobertura puede ser un contrato de futuros con la misma fecha de vencimiento que la opción o un contrato perpetuo, un producto innovador exclusivo del mercado de derivados de criptomonedas. Al reequilibrar la cobertura cada ocho horas (coincidiendo con el tiempo de financiación del contrato perpetuo) o diariamente, y utilizar contratos de futuros o contratos perpetuos con el mismo tiempo de vencimiento que el instrumento de cobertura, obtenemos unos resultados muy robustos. Además, en lugar de simplemente tabular los errores cuadráticos medios de diferentes ratios de cobertura como lo hicieron Coleman et al. (2001), Vähämaa (2004), Alexander et al. (2012) y muchos otros, aplicamos una prueba de razón de varianza simple. que proporciona la significancia estadística de la ganancia de eficiencia al utilizar un delta dado en relación con el delta de la estación base.

Utilizando este enfoque, demostramos que para las opciones fuera del dinero, el delta implícito en la curva sonriente (dinero pegajoso) es significativamente mejor que el delta Black-Scholes estándar en la cobertura, en algunos casos con más de un 40% de eficiencia. . El delta de varianza mínima también supera al delta de BS, pero solo para opciones dentro del dinero, ya que coincide con el delta del árbol fijo. Ningún otro delta ajustado por curva sonriente ha mejorado consistentemente al delta de BS, e incluso las coberturas del delta implícitas en la sonrisa y de varianza mínima tuvieron un desempeño deficiente durante gran parte de 2021. La única excepción es la cobertura implícita de sonrisa en las opciones de compra a corto plazo fuera del dinero cuando la pendiente de la curva de volatilidad implícita se torna positiva. En comparación con índices bursátiles como el S&P 500, los precios de Bitcoin no fluctúan hacia arriba de manera constante para luego caer repentinamente: sus aumentos de precio pueden ser tan grandes como sus disminuciones de precio, por lo que su curva de sonrisa puede ser muy simétrica o incluso inclinarse completamente hacia arriba. . También demostramos que los contratos perpetuos son mejores instrumentos de cobertura que los futuros con el mismo vencimiento que las opciones, independientemente del valor monetario de las opciones. Esto es particularmente evidente en las opciones a más largo plazo, donde la base entre los contratos perpetuos y los futuros es mayor.

Nuestra investigación se centra en marcos robustos sin modelos, que también son la opción preferida de muchos profesionales. No consideramos cobertura utilizando modelos estocásticos paramétricos y/o de volatilidad local por la sencilla razón de que la invariancia de escala de estos procesos significa que el delta es efectivamente libre de modelos y, por lo tanto, coincide con el delta implícito en smile utilizado en este estudio. Dado que introducimos el delta de varianza mínima robusta de Lee (2001) en nuestro estudio, creemos que agregar diferentes procesos de volatilidad estocástica para la cobertura delta dinámica es una cuestión de investigación menos relevante para la industria actual del comercio de criptomonedas.

Este artículo se centra en la cobertura delta dinámica con reequilibrio frecuente, que puede ayudar a los creadores de mercado en opciones de Bitcoin a obtener una ventaja competitiva en un mercado que recién está comenzando a madurar en 2021. Sin embargo, el mercado de Bitcoin ha crecido tan rápidamente que grandes traders profesionales como Jump Trading, Jane Street, XBTO y Cumberland DRW están negociando opciones de Bitcoin, a menudo con volúmenes diarios que superan los mil millones de dólares. También se están introduciendo muchas nuevas opciones de vencimiento y tamaños de contratos de opciones para satisfacer la demanda, por ejemplo, CME lanzó recientemente micro opciones de Bitcoin para operadores minoristas. A pesar de esto, el diferencial entre oferta y demanda de las opciones de Bitcoin sigue siendo relativamente grande, mucho más alto que el de los futuros de Bitcoin o los contratos perpetuos. Por lo tanto, la rentabilidad de la creación de mercado en el mercado de opciones de Bitcoin depende más de una cobertura delta dinámica precisa que de una cobertura delta-gamma-vega. Si el diferencial entre oferta y demanda de las opciones de Bitcoin disminuye en el futuro, puede ser interesante estudiar la cobertura gamma y vega del libro de opciones de Bitcoin. Sin embargo, al momento de escribir este artículo, los costos de transacción de usar opciones para cubrir el riesgo de precios y volatilidad pueden erosionar cualquier ganancia adicional que podría obtenerse a través de diferenciales más bajos.

declaración

Agradecemos a los revisores anónimos cuyos comentarios mejoraron significativamente el artículo.

Declaración de divulgación

Los autores declaran no tener conflictos de intereses.

Notas

1. Por el contrario, los deltas derivados de modelos no invariantes de escala, como el modelo de volatilidad local de Dupire (1994) o el modelo de árbol pegajoso de Derman y Kani (1994), no son teóricamente equivalentes a los deltas invariantes de escala. La varianza mínima Delta tampoco es una Delta invariante de escala, es la derivada total que incluye el efecto Vega de las correlaciones de volatilidad de precios distintas de cero.

2. Por ejemplo, véase el recienteArtículos de la CAIA, otro artículo sobre mediumartículo,así como risklatte y stackexchange Y varios foros de finanzas cuantitativas.

3. En esta literatura, Nastasi et al. (2020) calibran un modelo de consistencia de sonrisa para opciones de materias primas para capturar la dinámica de la sonrisa, mientras que Malz (2000) explica cómo tener en cuenta los ajustes de sonrisa al medir el riesgo de las opciones de divisas.

4. Las opciones de Deribit tienen vencimiento quincenal, quincenal, bimensual y trimestral, y pueden tener una duración de hasta 9 o 12 meses. Su activo subyacente es el “Índice Deribit BTC” (BTC), que es un promedio ponderado equitativamente de los últimos precios de Bitcoin en 11 bolsas, excluyendo los precios más altos y más bajos. Los 9 precios restantes se utilizan para calcular el índice. Actualmente, estos intercambios incluyen Binance, Bitfinex, Bitstamp, Bittrex, Coinbase Pro, Gemini, Huobi Global, Itbit, Kraken, LMAX Digital y OKEx, y el índice se actualiza cada segundo. Hay más fechas de vencimiento de opciones que fechas de vencimiento de futuros, por lo que para que Deribit incluya los precios de las opciones tanto para Bitcoin como para el USD, utilizan los mismos precios de futuros (posiblemente sintéticos) que las fechas de vencimiento de las opciones. Esto no significa que el contrato de futuros (posiblemente sintético) sea el subyacente. De hecho,Especificaciones de las opciones de Deribit Se indica claramente que el activo subyacente es el índice Deribit BTC. Para las opciones a corto plazo, el rango de ejercicio varía entre el 50% y el 150% del precio actual de BTC, y para las opciones con vencimientos superiores a 6 meses, el rango de ejercicio puede ser hasta el 800% del precio actual de BTC.

5. Véase tambiénDatos históricos de opciones de CBOE, para comprender el volumen de negociación de las opciones SPX en CBOE.

6. Véase tambiénVolumen de operaciones de opciones de Bitcoiny Opciones de Bitcoin de Goldman Sachs。

7. A continuación se encuentran CME (5%), OKEx (2,5%) y FTX y Bit.com, verThe Block Options。

8. Para calcular el rendimiento final, Deribit utiliza el índice BTC promedio 30 minutos antes del vencimiento como valor de liquidación. Para obtener más detalles, consulte el sitio web oficialEspecificaciones de las opciones de Deribit . Es importante tener en cuenta que el mercado de opciones de Bitcoin de Deribit no está completo. Los índices en sí no son negociables y requieren una replicación costosa y un reequilibrio frecuente. El mercado está incompleto para los comerciantes debido a la falta de información sobre el cálculo preciso del valor de liquidación. Sin embargo, una discusión detallada de esta cuestión está más allá del alcance de este artículo, y nos remitimos a Alexander et al. (2022a) para una discusión en profundidad.

9. Consulte 2022Mercado de criptomonedas descentralizado Categoría.

10. Los futuros inversos son contratos de futuros denominados en Bitcoin basados ​​en el precio en USD de Bitcoin o en el valor de un índice de Bitcoin. Tanto los futuros estándar como los inversos utilizan el valor del USD como subyacente, pero difieren en el método de liquidación: los futuros estándar de CME tienen un monto nocional de 0,1 o 5 bitcoins y se pagan en USD, mientras que el monto nocional de los futuros inversos es de \(1 o \)10. y pagadero en Bitcoin. Por otra parte, este mecanismo de pago conduce a un cálculo de ganancias y pérdidas (PnL) diferente. Para los futuros estándar, es necesario restar el precio de cierre del precio de apertura de los futuros y multiplicar el resultado por el monto nocional para obtener la ganancia o pérdida en dólares estadounidenses. Los futuros (y opciones) inversos tienen un procedimiento de liquidación diferente, que toma el inverso del precio de apertura menos el inverso del precio de cierre y luego multiplica el resultado por el monto nocional de la posición para obtener la ganancia o pérdida medida en Bitcoin. El “precio de apertura” y el “precio de cierre” aquí se refieren al valor en dólares del contrato de futuros en el momento de entrar y salir de la posición.

11. Véase tambiénTasa de financiación perpetua de Deribit, para obtener una descripción del cálculo de la tasa de financiación de Deribit.

12. Véase tambiénThe BlockoCoinglass. Es importante señalar que más de ocho bolsas mostraron volúmenes comerciales anormalmente altos. Sin embargo, pasamos por alto los numerosos intercambios que habían inflado artificialmente los volúmenes debido al comercio de lavado.

13. Esta aproximación también ha sido defendida por Coleman et al. (2001) y muchos otros.

14. Derman (1999) calificó el modelo SS como un “intento pobre” de replicar el modelo BS utilizando un árbol de volatilidad implícita.

15. Con excepción de las opciones de venta (m=0,7) y de compra (m=1,3) muy fuera del dinero, estas opciones están subnegociadas en la categoría de vencimiento a corto plazo. Solo pudimos calcular precios sintéticos el 75% de las veces, por lo que excluimos estas opciones de nuestros resultados finales.

16. Por supuesto, el valor de PCP para cada nivel de ejercicio será diferente. Dado que el comercio generalmente se concentra en opciones ATM, es difícil encontrar un nivel de ejercicio ITM/OTM en el que se negocien activamente tanto opciones de compra como de venta, por lo que utilizamos el valor PCP derivado del cálculo retrospectivo de opciones ATM. Interpolamos los valores PCP ATM para dos fechas de vencimiento adyacentes y usamos estos valores para obtener precios de opciones fijas sintéticas cuando sea necesario.

17. Por ejemplo, debido a que siempre mantenemos un contrato perpetuo en nuestra construcción, el asegurador debe pagar financiación cuando la base del contrato perpetuo es positiva y recibe financiación cuando la base es negativa. Lo opuesto es cierto para la cobertura de posiciones largas en opciones. En cualquier caso, de la Figura 7 podemos ver que la base del contrato perpetuo es cambiante, a veces positiva y a veces negativa. No es difícil escribir un algoritmo de cobertura que salga completamente de una posición cubierta antes de que expire el financiamiento, pero no saldrá si la posición cubierta recibe financiamiento. Hoy en día, este tipo de “estrategias de comisiones de financiación” son comunes entre los fondos de cobertura en mercados no regulados que no impiden que estos robots comerciales estratégicos operen. En cualquier caso, solo estamos sugiriendo agregar estrategias de financiación a las estrategias de cobertura y no estamos explorando posibles ganancias o pérdidas, ya que este no es un estudio de estrategias comerciales de alta frecuencia.

18. Para las opciones ATM, los deltas ST y MV son los mismos, por lo que los resultados son los mismos, pero solo en este caso.

Referencias

1. Alexander, C., Pricing, Hedging and Trading Financial Instruments. Market Risk Analysis III, 2008 (Wiley). [Google Scholar]

2. Alexander, C. and Nogueira, L., Model-free hedge ratios and scale invariant models. J. Bank. Finance, 2007a, 31, 1839–1861. [Crossref], [Web of Science ®], [Google Scholar]

3. Alexander, C. and Nogueira, L., Model-free price hedge ratios for homogeneous claims on tradable assets. Quant. Finance, 2007b, 7(5), 473–479. [Taylor & Francis Online], [Web of Science ®], [Google Scholar]

4. Alexander, C., Rubinov, A., Kalepky, M. and Leontsinis, S., Regime-dependent smile-adjusted delta hedging. J. Futures Mark., 2012, 32(3), 203–229. [Crossref], [Web of Science ®], [Google Scholar]

5. Alexander, C., Chen, D. and Imeraj, A., Inverse and quanto inverse options in a Black–Scholes world. SSRN Working Paper, 2022a. [Crossref], [[Google Scholar]](https://scholar.google.com/scholar?hl=en&q=Alexander%2C+C.%2C+Chen%2C+D.+and+Ime