Una poderosa herramienta para los operadores programáticos: algoritmo de actualización incremental para calcular la media y la varianza

Introducción

En el comercio programático, a menudo es necesario calcular promedios y variaciones, como calcular promedios móviles e indicadores de volatilidad. Cuando necesitamos cálculos de alta frecuencia y a largo plazo, es necesario retener datos históricos durante mucho tiempo, lo que es innecesario y consume recursos. Este artículo introduce un algoritmo de actualización en línea para calcular promedios ponderados y variaciones, que es particularmente importante para procesar flujos de datos en tiempo real y ajustar dinámicamente las estrategias comerciales, especialmente las estrategias de alta frecuencia.

Promedio simple y varianza

Si usamos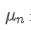Para representar el valor promedio del n-ésimo punto de datos, suponiendo que ya hemos calculado el promedio de n-1 puntos de datos /upload/asset/28e28ae0beba5e8a810a6.png, ahora recibimos un nuevo punto de datos /upload/asset/28d4723cf4cab1cf78f50.png. Queremos calcular el nuevo número promedio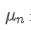La siguiente es una derivación detallada.

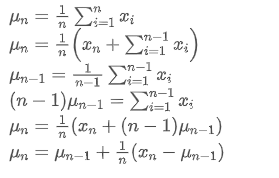
El proceso de actualización de la varianza se puede dividir en los siguientes pasos:

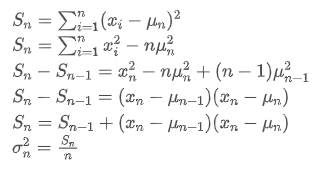
Como se puede ver en las dos fórmulas anteriores, este proceso nos permite actualizar nuevas medias y variaciones al recibir cada nuevo punto de datos.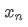Sin embargo, el problema es que lo que calculamos de esta manera son la media y la varianza de todas las muestras, mientras que en las estrategias reales, necesitamos considerar un cierto período fijo. Observar la actualización media anterior muestra que la cantidad de nuevas actualizaciones promedio es una desviación entre los nuevos datos y los promedios pasados multiplicados por una relación. Si esta relación se fija, dará lugar a un promedio ponderado exponencialmente, que discutiremos a continuación.

Promedio ponderado por exponenciales

El promedio ponderado exponencial puede definirse por la siguiente relación recursiva:

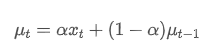
Entre ellos,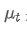es el promedio ponderado exponencial en el momento t,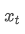es el valor observado en el momento t, α es el factor de peso, y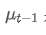es el promedio ponderado exponencial del punto de tiempo anterior.

Variancia ponderada exponencialmente

En cuanto a la varianza, necesitamos calcular el promedio ponderado exponencial de desviaciones al cuadrado en cada punto de tiempo.

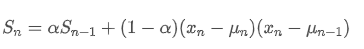
Entre ellos,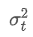es la varianza ponderada por exponenciales en el momento t, y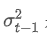es la varianza ponderada exponencial del punto de tiempo anterior.

Observe el promedio ponderado exponencialmente y la varianza, sus actualizaciones incrementales son intuitivas, conservando una parte de los valores pasados y agregando nuevos cambios.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA y EMA

La SMA (también conocida como media aritmética) y la EMA son dos medidas estadísticas comunes, cada una con características y usos diferentes. La primera asigna el mismo peso a cada observación, reflejando la posición central del conjunto de datos. La última es un método de cálculo recursivo que da un mayor peso a las observaciones más recientes. Los pesos disminuyen exponencialmente a medida que aumenta la distancia del tiempo actual para cada observación.

• Distribución del peso: La SMA asigna la misma ponderación a cada punto de datos, mientras que la EMA da una mayor ponderación a los puntos de datos más recientes.
• Sensibilidad a la nueva información: El SMA no es lo suficientemente sensible a los datos recién añadidos, ya que implica el recálculo de todos los puntos de datos.
• Complejidad computacional: El cálculo de la SMA es relativamente sencillo, pero a medida que aumenta el número de puntos de datos, también lo hace el costo computacional.

Método de conversión aproximado entre EMA y SMA

Aunque SMA y EMA son conceptualmente diferentes, podemos hacer que la EMA se aproxime a una SMA que contiene un número específico de observaciones eligiendo un valor α apropiado.

SMA es la media aritmética de todos los precios dentro de una ventana de tiempo dada. Para una ventana de tiempo N, el centroide de la SMA (es decir, la posición donde se encuentra el número promedio) se puede considerar como:

el centroide de la SMA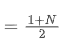

El EMA es un tipo de promedio ponderado en el que los puntos de datos más recientes tienen un mayor peso.

el centroide de la EMA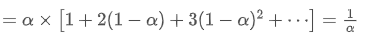

Cuando asumimos que SMA y EMA tienen el mismo centroide, podemos obtener:

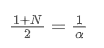
Para resolver esta ecuación, podemos obtener la relación entre α y N.

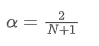
Esto significa que para una SMA dada de N días, el valor α correspondiente se puede utilizar para calcular una EMA equivalente, de modo que tengan el mismo centroide y los resultados sean muy similares.

Conversión de la EMA con diferentes frecuencias de actualización

Supongamos que tenemos una EMA que se actualiza cada segundo, con un factor de peso de /upload/asset/28da19ef219cae323a32f.png. Esto significa que cada segundo, el nuevo punto de datos se agregará a la EMA con un peso de /upload/asset/28da19ef219cae323a32f.png, mientras que la influencia de los puntos de datos antiguos se multiplicará por /upload/asset/28cfb008ac438a12e1127.png.

Si cambiamos la frecuencia de actualización, como actualizar una vez cada f segundos, queremos encontrar un nuevo factor de peso /upload/asset/28d2d28762e349a03c531.png, para que el impacto general de los puntos de datos dentro de f segundos sea el mismo que cuando se actualiza cada segundo.

Dentro de f segundos, si no se realizan actualizaciones, el impacto de los puntos de datos antiguos se decaerá continuamente f veces, cada vez multiplicado por /upload/asset/28e50eb9c37d5626d6691.png. Por lo tanto, el factor de decaimiento total después de f segundos es /upload/asset/28e296f97d8c8344a2ee6.png.

Para que la EMA actualizada cada f segundos tenga el mismo efecto de desintegración que la EMA actualizada cada segundo dentro de un período de actualización, establecemos el factor de desintegración total después de f segundos igual al factor de desintegración dentro de un período de actualización:

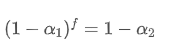
Resolviendo esta ecuación, obtenemos nuevos factores de peso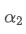

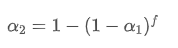
Esta fórmula proporciona el valor aproximado del nuevo factor de peso /upload/asset/28d2d28762e349a03c531.png, que mantiene el efecto de suavizado de la EMA sin cambios cuando cambia la frecuencia de actualización.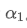con un valor de 0,001 y actualizarlo cada 10 segundos, si se cambia a una actualización cada segundo, el valor equivalente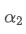sería aproximadamente 0,01.

Implementación de código Python

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Resumen de las actividades

En el comercio programático de alta frecuencia, el procesamiento rápido de datos en tiempo real es crucial. Para mejorar la eficiencia computacional y reducir el consumo de recursos, este artículo introduce un algoritmo de actualización en línea para calcular continuamente el promedio ponderado y la varianza de un flujo de datos. Las actualizaciones incrementales en tiempo real también se pueden usar para varios cálculos de datos estadísticos e indicadores, como la correlación entre los precios de dos activos, el ajuste lineal, etc., con un gran potencial. La actualización incremental trata los datos como un sistema de señales, que es una evolución en el pensamiento en comparación con los cálculos de período fijo.