Medir el riesgo y el rendimiento - Una introducción a la teoría de Markowitz
El autor:FMZ~Lydia, Creado: 2023-11-13 11:05:54, Actualizado: 2024-11-08 09:07:17
La semana pasada, al introducirCómo medir el riesgo de posición - Introducción al método VaR, se mencionó que el riesgo de una cartera no es igual a los riesgos de los activos individuales y está relacionado con su correlación de precios. Tomando dos activos como ejemplo, si su correlación positiva es muy fuerte, lo que significa que suben y caen juntos, entonces las inversiones diversificadas no reducirán el riesgo. Si hay una fuerte correlación negativa, las inversiones diversificadas pueden reducir el riesgo significativamente.
La Teoría Moderna de la Cartera (MPT), propuesta por Harry Markowitz en 1952, es un marco matemático para la selección de carteras. Su objetivo es maximizar los rendimientos esperados eligiendo diferentes combinaciones de activos de riesgo mientras se controla el riesgo. La idea central es que los precios de los activos no se mueven completamente sincronizados entre sí (es decir, existe una correlación incompleta entre los activos), y el riesgo general de inversión se puede reducir a través de una asignación diversificada de activos.
El concepto clave de la teoría de Markowitz
- Rentabilidad esperada: Es el rendimiento que los inversores esperan recibir de la tenencia de activos o de una cartera de inversiones, generalmente previsto sobre la base de datos históricos de rendimiento.
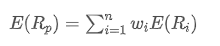
¿Dónde?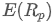 es el rendimiento esperado de la cartera,
es el rendimiento esperado de la cartera,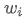 es el peso del i-ésimo activo de la cartera,
es el peso del i-ésimo activo de la cartera,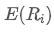 es el rendimiento esperado del activo i.
es el rendimiento esperado del activo i.
- El riesgo (volatilidad o desviación estándar): Se utiliza para medir la incertidumbre de los rendimientos de las inversiones o la volatilidad de las inversiones.
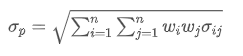
¿Dónde?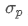 representa el riesgo total de la cartera,
representa el riesgo total de la cartera,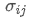 es la covarianza del activo i y del activo j, que mide la relación de cambio de precio entre estos dos activos.
es la covarianza del activo i y del activo j, que mide la relación de cambio de precio entre estos dos activos.
- Covariancia: Mide la relación mutua entre los cambios de precios de dos activos.
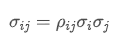
¿Dónde?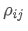 es el coeficiente de correlación del activo i y del activo j,
es el coeficiente de correlación del activo i y del activo j,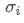 y
y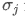 son, respectivamente, las desviaciones tipo del activo i y del activo j.
son, respectivamente, las desviaciones tipo del activo i y del activo j.
- Fronteras eficientes: En el sistema de coordenadas riesgo-rendimiento, la frontera eficiente es el conjunto de carteras de inversión que pueden proporcionar el rendimiento máximo esperado a un nivel de riesgo determinado.
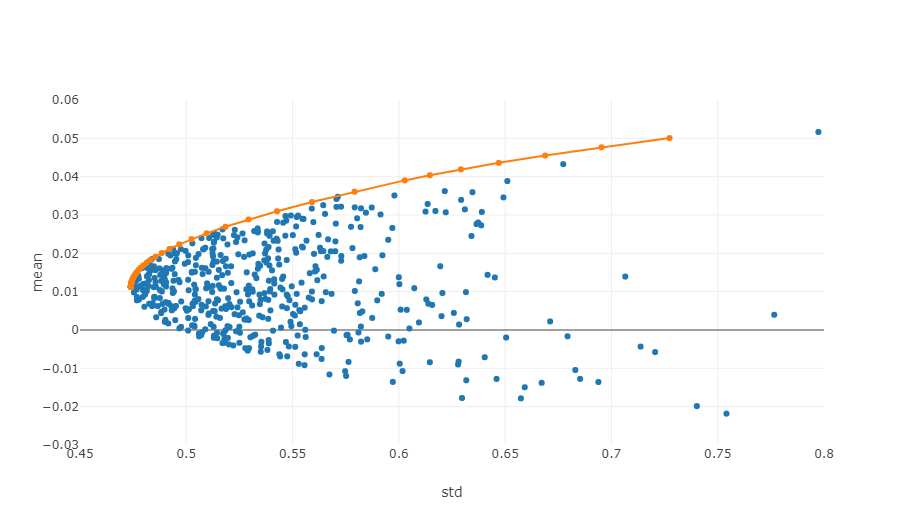
El diagrama anterior es una ilustración de una frontera eficiente, donde cada punto representa una cartera de inversión ponderada diferente. El eje x denota la volatilidad, que equivale al nivel de riesgo, mientras que el eje y significa la tasa de retorno.
En el comercio cuantitativo y la gestión de carteras, la aplicación de estos principios requiere el análisis estadístico de datos históricos y el uso de modelos matemáticos para estimar los rendimientos esperados, desviaciones estándar y covariancias para varios activos. Luego se utilizan técnicas de optimización para encontrar la mejor asignación de peso de activos. Este proceso a menudo implica operaciones matemáticas complejas y un extenso procesamiento informático, por lo que el análisis cuantitativo se ha vuelto tan importante en las finanzas modernas.
Ejemplo de código Python para encontrar la combinación óptima utilizando el método de simulación
El cálculo de la cartera óptima de Markowitz es un proceso de varios pasos, que implica varios pasos clave, como la preparación de datos, la simulación de cartera y el cálculo de indicadores.https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/
- Obtención de datos de mercado:
A través de laget_dataEn el caso de las monedas digitales, la función es obtener los datos de precios históricos de la moneda digital seleccionada, los datos necesarios para calcular los rendimientos y los riesgos, que se utilizan para construir carteras de inversión y calcular los ratios Sharpe.
- Calcular la tasa de rendimiento y el riesgo:
Elcalculate_returns_riskEsta función se utilizó para calcular los rendimientos anualizados y el riesgo anualizado (desviación estándar) para cada moneda digital.
- Calcular la cartera óptima de Markowitz:
Elcalculate_optimal_portfolioEn cada simulación, se generaron ponderaciones aleatorias de activos y luego se calculó el rendimiento y el riesgo esperados de la cartera sobre la base de estas ponderaciones.
Al generar al azar combinaciones con diferentes pesos, es posible explorar múltiples carteras de inversión potenciales para encontrar la óptima.
El objetivo de todo el proceso es encontrar la cartera de inversiones que produzca los mejores rendimientos esperados a un nivel de riesgo dado. Al simular múltiples combinaciones posibles, los inversores pueden comprender mejor el rendimiento de diferentes configuraciones y elegir la combinación que mejor se adapte a sus objetivos de inversión y tolerancia al riesgo. Este método ayuda a optimizar las decisiones de inversión, haciendo que las inversiones sean más efectivas.
import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt
# Obtain market data
def get_data(symbols):
data = []
for symbol in symbols:
url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
res = requests.get(url)
data.append([float(line[4]) for line in res.json()])
return data
def calculate_returns_risk(data):
returns = []
risks = []
for d in data:
daily_returns = np.diff(d) / d[:-1]
annualized_return = np.mean(daily_returns) * 365
annualized_volatility = np.std(daily_returns) * np.sqrt(365)
returns.append(annualized_return)
risks.append(annualized_volatility)
return np.array(returns), np.array(risks)
# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
n_assets = len(returns)
num_portfolios = 3000
results = np.zeros((4, num_portfolios), dtype=object)
for i in range(num_portfolios):
weights = np.random.random(n_assets)
weights /= np.sum(weights)
portfolio_return = np.sum(returns * weights)
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))
results[0, i] = portfolio_return
results[1, i] = portfolio_risk
results[2, i] = portfolio_return / portfolio_risk
results[3, i] = list(weights) # Convert weights to a list
return results
symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)
returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)
max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]
# Output results
print("Optimal combination:")
for i in range(len(symbols)):
print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")
print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")
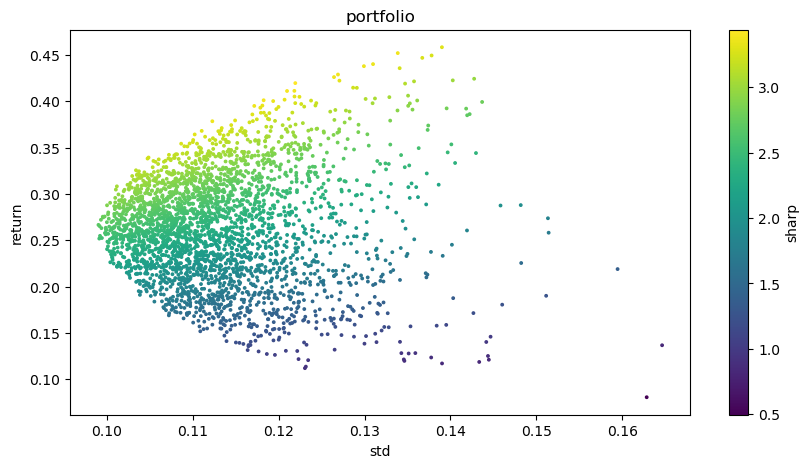
# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()
Resultado de salida final: La combinación óptima: Peso del BTCUSDT: 0,0721 Peso del ETHUSDT: 0.2704 Peso del BNBUSDT: 0,3646 Peso del LINKUSDT: 0,1892 Peso del BCHUSDT: 0,0829 Peso del LTCUSDT: 0,0209 Tasa de rendimiento esperada: 0,4195 Riesgo esperado (desviación tipo): 0,1219 Sharpe ratio: 3,4403
- ¿Cuál es el mejor para copiar: el valor de mercado bajo o el precio bajo?
- Bayes - Descifrando el misterio de la probabilidad, explorando la sabiduría matemática detrás de la toma de decisiones
- Bayes: el secreto de descifrar las probabilidades y la inteligencia matemática detrás de las decisiones
- Las ventajas de utilizar la API ampliada de FMZ para una gestión eficiente del control de grupo en el comercio cuantitativo
- Resultados del precio después de que la moneda sea incluida en contratos perpetuos
- Utiliza la API de extensión de FMZ para lograr una administración de control de grupo eficiente con ventajas en transacciones cuantitativas
- El precio de las monedas después de la entrada en línea de un contrato perpetuo
- La correlación entre el aumento y la caída de las monedas y Bitcoin
- Relación entre la caída de la moneda y el Bitcoin
- Una breve discusión sobre el equilibrio de los libros de pedidos en los intercambios centralizados
- Hablar sobre el balance del libro de pedidos de la bolsa centralizada
- La medida de los riesgos y las recompensas La teoría de Tom Markowitz
- Una poderosa herramienta para los operadores programáticos: algoritmo de actualización incremental para calcular la media y la varianza
- Utilidad para los comerciantes programados: algoritmo de actualización incremental para calcular medias y diferencias
- Construcción y aplicación del ruido del mercado
- Mejora y transformación del factor PSY
- Análisis de la estrategia de negociación de alta frecuencia - Penny Jump
- Ideas de negociación alternativas - Estrategia de negociación en el área de la línea K
- Construcción y aplicación del ruido del mercado
- Factor PSY (línea psicológica) de actualización y transformación