Bayes: el secreto de descifrar las probabilidades y la inteligencia matemática detrás de las decisiones

La estadística de Bayes es una disciplina universitaria fuerte en el campo de las matemáticas, con una amplia gama de aplicaciones en muchos campos, incluyendo finanzas, investigación médica e información. Permite a los científicos combinar creencias anteriores con evidencia para extraer nuevas creencias posteriores que nos permitan tomar decisiones más inteligentes.

En este artículo, vamos a dar una breve introducción a algunos de los principales matemáticos que fundaron este campo.

Antes de Bayes Para comprender mejor la estadística bayesiana, necesitamos volver al siglo XVIII y referirnos al matemático De Moivre y a su trabajo sobre el principio de la casualidad.

En su trabajo, De Moivre resolvió muchos problemas de su época relacionados con la probabilidad y el juego. Como usted puede saber, su solución a uno de estos problemas condujo al origen de la distribución normal, pero esa es otra historia.

En su trabajo, hay una pregunta muy sencilla:

Los jugadores lanzan una moneda justa tres veces consecutivas y obtienen tres probabilidades positivas.

Al leer los problemas descritos en el cuadro de principios de la oportunidad, es posible que note que la mayoría de los problemas comienzan con una hipótesis y luego calculan la probabilidad de un evento dado. Por ejemplo, en el problema anterior, hay una hipótesis que dice que la moneda es justa y, por lo tanto, la probabilidad de obtener un positivo en el lanzamiento es de 0.5.

Esto se expresa hoy en día en términos matemáticos como:

𝑃(𝑋|𝜃)

Pero ¿y si no sabemos si la moneda es justa?𝜃¿Qué es eso?

El año pasado, el número de personas que se suicidaron fue de más de 1.000.

Casi cincuenta años más tarde, en 1763, un trabajo titulado "El problema en el principio de la solución de la culebración"[2] fue publicado en el periódico de la Sociedad Real de Londres, The Philosophical Exchange of Culebración.

En las primeras páginas del documento, hay un texto escrito por el matemático Richard Price que resume el contenido de un artículo escrito por su amigo Thomas Bayes en los años previos a su muerte. En la introducción, Price explica la importancia de algunos descubrimientos hechos por Thomas Bayes, que no están incluidos en el teorema de probabilidad de De Moivre.

De hecho, él se refiere a un problema específico:

El número de veces que ocurre y falla un evento desconocido conocido, y la probabilidad de que ocurra entre dos probabilidades nombradas.

En otras palabras, después de observar un evento, encontramos un parámetro desconocido.θ¿Cuál es la probabilidad entre dos grados de probabilidad?. Este es en realidad uno de los primeros problemas relacionados con la inferencia estadística en la historia, y dio origen al nombre de probabilidad inversa.

𝑃( 𝜃 | 𝑋）

Esta, por supuesto, es la distribución posterior que hoy conocemos como el teorema de Bayes.

Causas sin causa

En el video, los padres de la iglesia se encuentran en un lugar llamado "La Casa de los Reyes".En la actualidad, la mayoría de las personas que viven en la ciudad de Nueva York son de la misma etnia.y¿Qué es lo que está sucediendo?Pero para hacer esto, necesitamos dejar de lado temporalmente algo de conocimiento sobre estadística.

Estamos en el siglo XVIII, y la probabilidad está siendo un área de creciente interés para los matemáticos. Matemáticos como DeMohr o Bernoulli ya han demostrado que algunos eventos ocurren con cierto grado de azar, pero que siguen estando gobernados por reglas fijas. Por ejemplo, si usted juega el dedo varias veces, una sexta parte de las veces se detiene en seis.

Ahora, imagine que usted es un matemático y un creyente devoto que vive en esta época. Tal vez le interese conocer esta ley oculta y su relación con Dios.

Este es, de hecho, el problema que Bayes y Price se preguntan. Quieren resolver este problema aplicando directamente la solución a la prueba de que el universo de la sabiduría debe ser el resultado de la inteligencia y la inteligencia; por lo tanto, la prueba de la existencia de Dios con la causa final es la sabiduría[2] - es decir, una causa sin causa.

¿Qué es esto?

Sorprendentemente, aproximadamente dos años más tarde, en 1774, aparentemente sin haber leído el artículo de Thomas Bayes, el matemático francés Laplace escribió un artículo titulado "La causa de los eventos relacionados con la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por la probabilidad de que los eventos causados por

Los principios principales:

Si un evento puede ser causado por n causas diferentes, entonces la proporción entre las probabilidades de estas causas de un evento dado es igual a la probabilidad de que ocurra una causa dada, y la probabilidad de que cada una de estas causas exista es igual a la probabilidad de que ocurra una causa de un evento dado, dividida por la suma de las probabilidades de que cada una de estas causas ocurra.

Este es el teorema de Bayes que conocemos hoy:

​

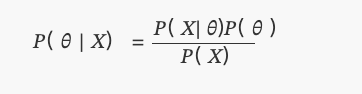
Entre ellasP(θ)La distribución es uniforme.

El experimento de las monedas

Vamos a llevar las estadísticas de Bayes a la actualidad usando Python y la biblioteca PyMC y hacer un simple experimento.

Supongamos que un amigo te da una moneda y te pregunta si crees que es una moneda justa. Porque él tiene prisa, él te dice que sólo puede tirar 10 monedas. Como puedes ver, hay un parámetro desconocido en este problema.pAsí que la probabilidad de obtener un positivo en el lanzamiento de monedas, y queremos estimar esto, es decir, la probabilidad de obtener un positivo en el lanzamiento de monedas.pEl valor más probable de los valores de los números de los números de los números de los números de los números de los números.

(Nota: no estamos hablando de parámetros)pEs una variable aleatoria, sino que el parámetro es fijo, y queremos saber entre qué valores es más probable que esté.

Para tener una visión diferente del tema, vamos a abordarlo bajo dos creencias previas diferentes:

• 1, usted no tiene información previa sobre la equidad de la moneda y asigna una probabilidad igual apEn este caso, vamos a usar lo que se llama un antecedente sin información, ya que no agregaste ninguna información a tus creencias.

• 2o, por experiencia sabes que aunque una moneda pueda ser injusta, es difícil hacerla muy injusta, por lo que piensas que los parámetros son muy diferentes.pEs muy probable que no sea inferior a 0.3 o superior a 0.7; en este caso, vamos a usar un tipo de precedencia de información.

Para ambas situaciones, nuestras creencias previas serían las siguientes:

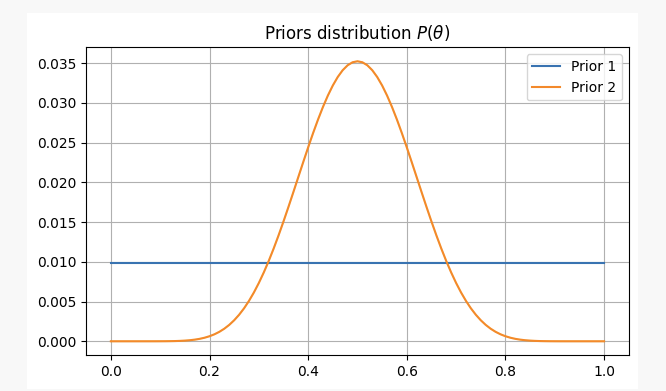
Después de lanzar una moneda 10 veces, usted tiene dos resultados positivos. Con esta prueba, es muy probable que encontremos nuestros parámetros en el lugar.p？

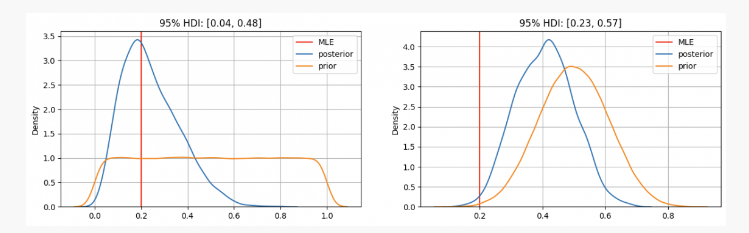
Así que, como se puede ver, en el primer caso, estamos haciendo un parámetro.pLa distribución previa se centra en el estimado de máxima similitud (MLE).p=0.2, que es similar al método de la escuela de frecuencias. Los parámetros verdaderamente desconocidos estarán dentro del intervalo de confianza del 95%, entre 0.04 y 0.48;

Por otro lado, hay una alta confianza en que los parámetrospEn el caso de que se encuentre entre 0.3 y 0.7, podemos ver una distribución posterior de alrededor de 0.4, muy superior al valor dado por nuestro MLE. En este caso, los parámetros verdaderamente desconocidos estarán dentro del intervalo de confianza del 95%, entre 0.23 y 0.57.

Por lo tanto, en el primer caso, le dirías a tu amigo que estás seguro de que la moneda es injusta; pero en el otro caso, le dirás que no puedes estar seguro de si la moneda es justa.

Como puedes ver, incluso con la misma evidencia (dos positivos en cada 10 proyecciones), los resultados son diferentes bajo diferentes creencias previas. Esta es una ventaja de la estadística bayesiana, similar al método científico, que nos permite actualizar nuestras creencias combinando creencias previas con nuevas observaciones y pruebas.

Enlace a la sección

En el artículo de hoy, vemos los orígenes de la estadística bayesiana y sus principales contribuyentes.转载自quantdare.com。