Modelado y análisis de la volatilidad de Bitcoin basado en el modelo ARMA-EGARCH

Recientemente, he hecho un análisis sobre la volatilidad de Bitcoin, que es verbal y espontánea. Así que simplemente comparto algo de mi comprensión y código de la siguiente manera. Mi capacidad es limitada, y el código no es muy perfecto. Si hay algún error, por favor señalalo y corríjelo directamente.

1. Una breve descripción de las series temporales de las finanzas

La serie temporal de las finanzas es un conjunto de modelos de series de procesos estocásticos basados en una variable observada en la dimensión temporal. La variable es generalmente la tasa de rendimiento de los activos.

Aquí, se asume audazmente que la tasa de rendimiento de Bitcoin se ajusta a las características de la tasa de rendimiento de los activos financieros generales, es decir, es una serie débilmente suave, que se puede demostrar mediante pruebas de consistencia de varias muestras.

Preparados, bibliotecas de importación, funciones de encapsulación

La configuración del entorno de investigación está completa. La biblioteca requerida para los cálculos posteriores se importa aquí. Como se escribe intermitentemente, puede ser redundante. Por favor, limpielo usted mismo.

En [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Fuera de juego[1]: (Bilancio: 10000,0 FrozenBalance: 0,0 Reservas: 0,0 FrozenStocks: 0,0)

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

En [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

Comencemos con una breve comprensión de los datos históricos de Bitcoin

Desde un punto de vista estadístico, podemos echar un vistazo a algunas características de datos de Bitcoin. Tomando la descripción de datos del año pasado como ejemplo, la tasa de retorno se calcula de una manera simple, es decir, el precio de cierre se resta logarítmicamente. La fórmula es la siguiente: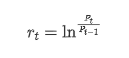

En [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Fuera[3]: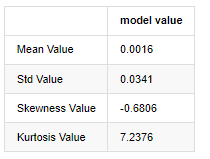

La característica de las colas de grasa gruesa es que cuanto más corta sea la escala de tiempo, más significativa es la característica.

Tomando como ejemplo los datos diarios del precio de cierre desde el 1 de enero de 2019 hasta el presente, hacemos un análisis descriptivo de su tasa de retorno logarítmico, y se puede ver que la serie de tasa de retorno simple de Bitcoin no se ajusta a la distribución normal, y tiene la característica obvia de colas gruesas.

El valor medio de la secuencia es 0.0016, la desviación estándar es 0.0341, la sesga es -0.6819, y la kurtosis es 7.2243, que es mucho mayor que la distribución normal y tiene la característica de colas gruesas.

En [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Fuera[4]:

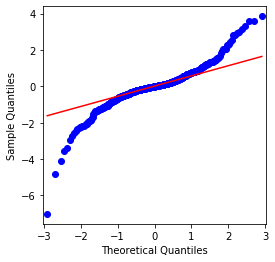
Se puede ver que el gráfico QQ es perfecto, y la serie de retorno logarítmico para Bitcoin no se ajusta a una distribución normal de los resultados, y tiene una característica obvia de colas gruesas.

A continuación, echemos un vistazo al efecto de agregación de volatilidad, es decir, las series temporales financieras a menudo van acompañadas de una mayor volatilidad después de una mayor volatilidad, mientras que una menor volatilidad generalmente es seguida de una menor volatilidad.

La agrupación de volatilidad refleja los efectos de retroalimentación positivos y negativos de la volatilidad y está altamente correlacionada con las características de las colas de grasa. Econométricamente, esto implica que las series temporales de volatilidad pueden estar autocorrelacionadas, es decir, la volatilidad del período actual puede tener alguna relación con el período anterior, el segundo período anterior o incluso el tercer período anterior.

En [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Fuera[5]:

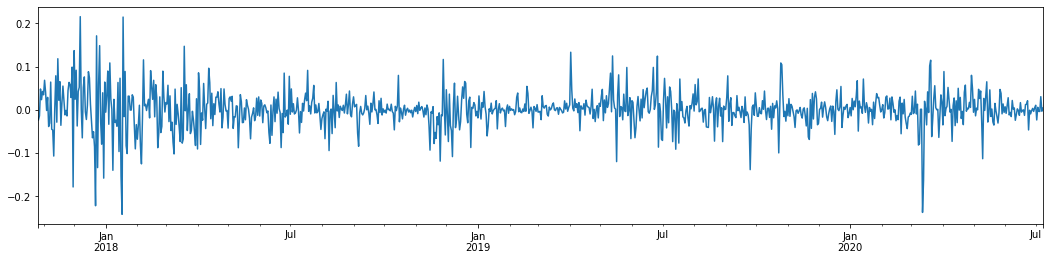
Si tomamos la tasa logarítmica diaria de rendimiento de Bitcoin en los últimos 3 años y la trazamos, se puede ver claramente el fenómeno de agrupación de volatilidad. Después del mercado alcista en Bitcoin en 2018, estuvo en una posición estable la mayor parte del tiempo. Como podemos ver en la extrema derecha, en marzo de 2020, a medida que los mercados financieros globales cayeron, también hubo una carrera en la liquidez de Bitcoin, con rendimientos que cayeron casi un 40% en un día, con fuertes oscilaciones negativas.

En una palabra, a partir de la observación intuitiva, podemos ver que una gran fluctuación será seguida por una fluctuación densa con una gran probabilidad, que también es el efecto de agregación de la volatilidad.

1-3. Preparación de los datos

Para preparar el conjunto de muestras de entrenamiento, primero establecemos una muestra de referencia, en la que la tasa de retorno logarítmica es la volatilidad observada equivalente.

El método de muestreo de nuevo se basa en datos horarios y la fórmula se muestra de la siguiente manera: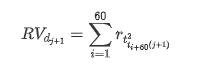

En [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Fuera[4]: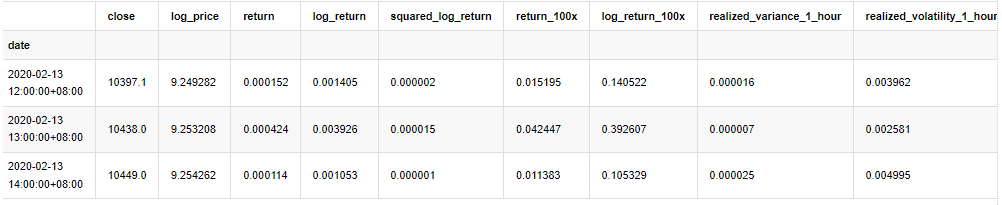

Preparar los datos fuera de la muestra de la misma manera

En [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Para comprender los datos básicos de la muestra, se realiza un simple análisis descriptivo de la siguiente manera:

En [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Fuera[9]:

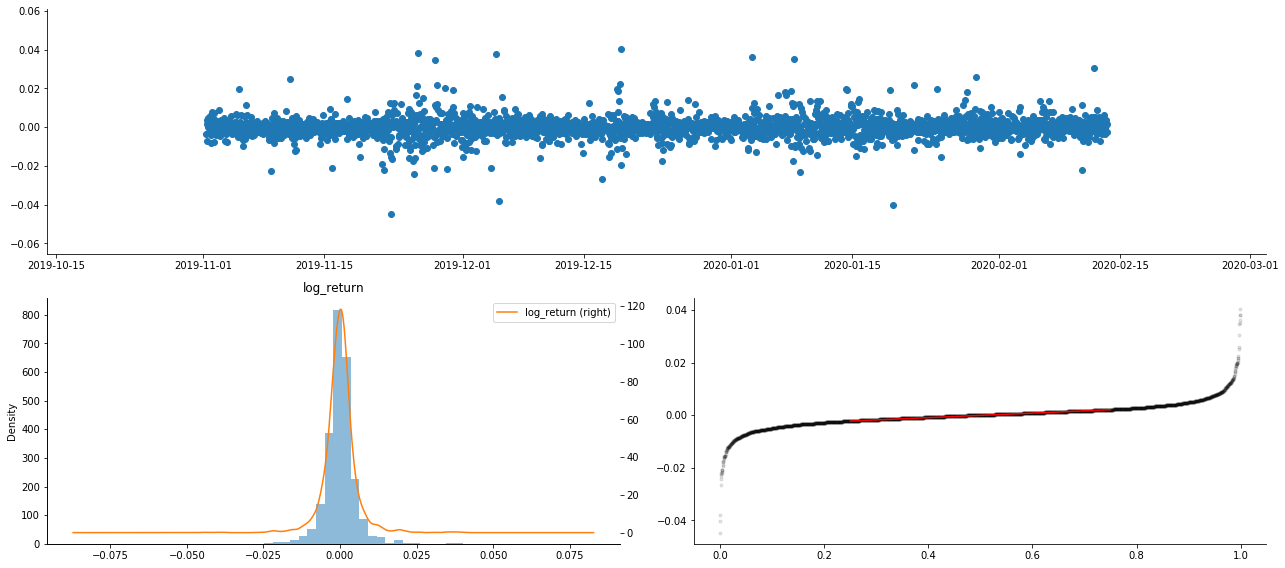
Como resultado, existe una agregación obvia de volatilidad y un efecto de apalancamiento en el gráfico de series temporales de rendimientos logarítmicos.

La desviación en el gráfico de distribución de los retornos logarítmicos es menor que 0, lo que indica que los retornos en la muestra son ligeramente negativos y sesgados a la derecha.

La desviación de la distribución de los datos es inferior a 1, lo que indica que los resultados dentro de la muestra son ligeramente positivos y ligeramente sesgados hacia la derecha.

Ahora que hemos llegado a este punto, hagamos otra prueba estadística. En [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Fuera[7]:

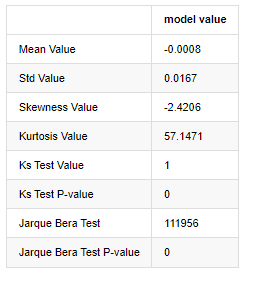
Se utilizan las estadísticas de prueba de Kolmogorov-Smirnov y Jarque-Bera respectivamente. La hipótesis original se caracteriza por una diferencia significativa y una distribución normal. Si el valor P es menor que el valor crítico del nivel de confianza del 0,05%, se rechaza la hipótesis original.

Se puede ver que el valor de cortosis es mayor que 3, lo que muestra las características de las colas de grasa gruesa. Los valores de P de KS y JB son menores que el intervalo de confianza. Se rechaza la suposición de distribución normal, lo que demuestra que la tasa de retorno de BTC no tiene las características de la distribución normal, y el estudio empírico tiene las características de las colas de grasa gruesa.

1-4. Comparación de la volatilidad real y la observada

Combinamos el log_retorno al cuadrado (rendimiento logarítmico al cuadrado) y la varianza realizada (varianza realizada) para las observaciones.

En [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Fuera [11]:

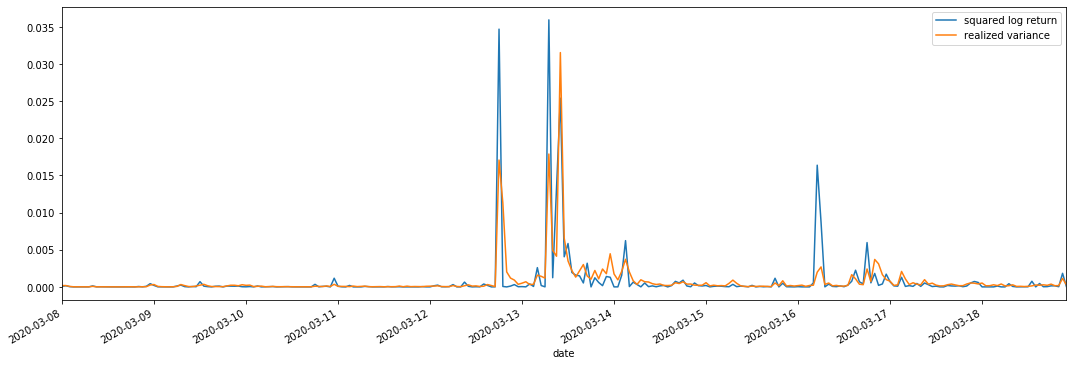
Se puede ver que cuando el rango de varianza realizado es mayor, la volatilidad del rango de tasa de retorno también es mayor, y la tasa de retorno realizada es más suave.

Desde un punto de vista puramente teórico, RV está más cerca de la volatilidad real, mientras que la volatilidad a corto plazo se suaviza debido a que la volatilidad intradiaria pertenece a los datos de la noche a la mañana, por lo que desde un punto de vista observacional, la volatilidad intradiaria es más adecuada para una menor frecuencia de volatilidad del mercado de valores.

2. Fluidez de las series temporales

Si es una serie no estacionaria, debe ajustarse aproximadamente a una serie estacionaria. La forma común es hacer el procesamiento de diferencias. Teóricamente, después de muchas veces de diferencia, la serie no estacionaria se puede aproximar a una serie estacionaria. Si la covarianza de la serie de muestras es estable, la expectativa, la varianza y la covarianza de sus observaciones no cambiarán con el tiempo, lo que indica que la serie de muestras es más conveniente para la inferencia en el análisis estadístico.

En este caso se utiliza la prueba de raíz de la unidad, es decir, la prueba ADF. La prueba ADF utiliza la prueba t para observar la significación. En principio, si la serie no muestra una tendencia obvia, solo se retienen elementos constantes. Si la serie tiene tendencia, la ecuación de regresión debe incluir elementos constantes y elementos de tendencia temporal. Además, se pueden usar criterios AIC y BIC para la evaluación basada en criterios de información. Si se requiere una fórmula, es la siguiente: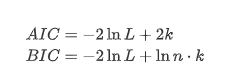

En [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Fuera[8]: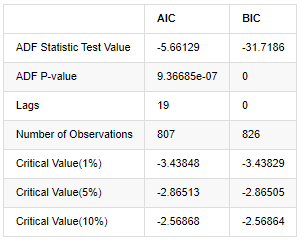

La suposición original es que no hay raíz unitaria en la serie, es decir, la suposición alternativa es que la serie es estacionaria.

3. Identificación del modelo y determinación del pedido

Para establecer la ecuación de valor medio, es necesario hacer una prueba de autocorrelación en la secuencia para asegurarse de que el término de error no tenga autocorrelación.

En [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Fuera [1]:

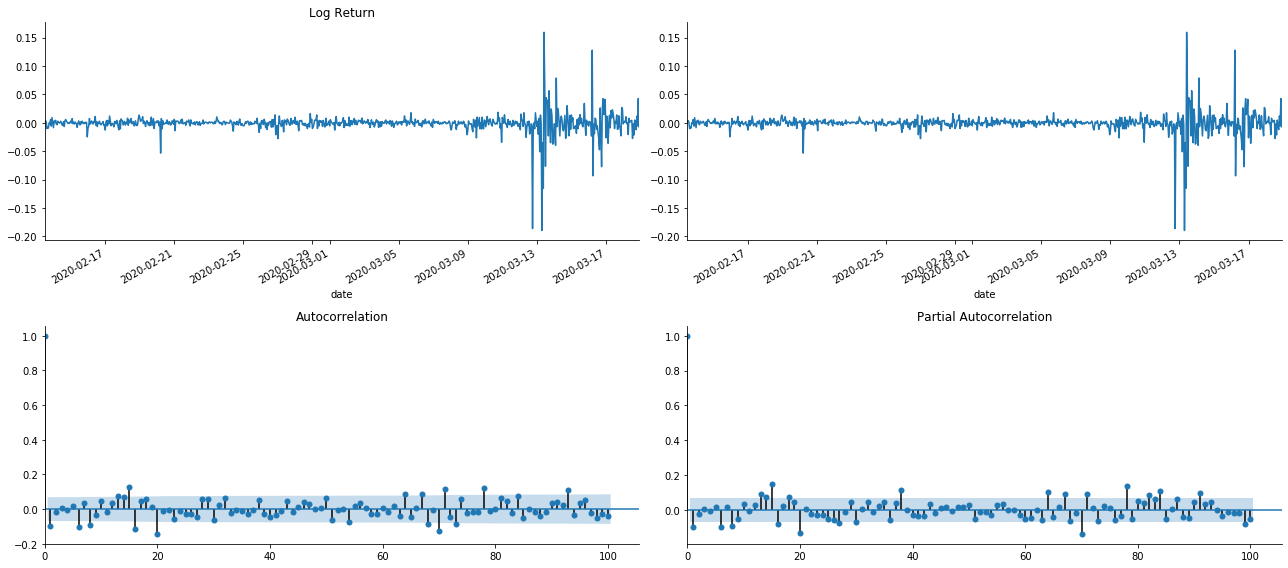
Se puede ver que el efecto de truncado es perfecto. En ese momento, esta imagen me dio una inspiración. ¿Es el mercado realmente inválido? Para verificar, vamos a hacer un análisis de autocorrelación en la serie de retorno y determinar el orden de retraso del modelo.

El coeficiente de correlación comúnmente utilizado es para medir la correlación entre él y sí mismo, es decir, la correlación entre r(t) y r (t-l) en un cierto momento en el pasado: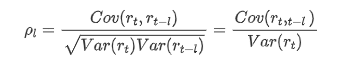

Entonces hagamos una prueba cuantitativa. La suposición original es que todos los coeficientes de autocorrelación son 0, es decir, no hay autocorrelación en la serie.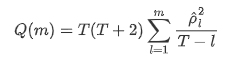

Se tomaron diez coeficientes de autocorrelación para el análisis, como sigue:

En [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Fuera[9]: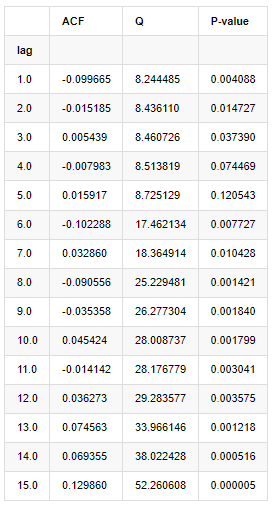

De acuerdo con la estadística de prueba Q y el valor P, podemos ver que la función de autocorrelación ACF gradualmente se convierte en 0 después del orden 0. Los valores P de las estadísticas de prueba Q son lo suficientemente pequeños como para rechazar la suposición original, por lo que hay autocorrelación en la serie.

4. Modelado ARMA

Los modelos AR y MA son bastante simples. En pocas palabras, Markdown está demasiado cansado para escribir fórmulas. Si estás interesado, por favor comprueba tú mismo. El modelo AR (Autorregressión) se utiliza principalmente para modelar series de tiempo. Si la serie ha superado la prueba ACF, es decir, el coeficiente de autocorrelación con un intervalo de 1 es significativo, es decir, los datos en el tiempo pueden ser útiles para predecir el tiempo t.

El modelo MA (media móvil) utiliza la interferencia aleatoria o la predicción de errores de los períodos q pasados para expresar el valor de predicción actual de manera lineal.

Para describir completamente la estructura dinámica de los datos, es necesario aumentar el orden de los modelos AR o MA, pero tales parámetros harán que el cálculo sea más complejo.

Dado que las series de tiempo de precios son generalmente no estacionarias, y el efecto de optimización del método de diferencia en la estacionalidad se ha discutido anteriormente, el modelo ARIMA (p, d, q) (media móvil autorregressiva de suma) agrega procesamiento de diferencia de orden d sobre la base de la aplicación de modelos existentes a las series.

En una palabra, la única diferencia entre el modelo ARIMA y el proceso de construcción del modelo ARMA es que si se obtienen los resultados inestables después de analizar la estabilidad, el modelo hará una diferencia cuadrática a la serie directamente y luego realizará la prueba de estabilidad, y luego determinará el orden p y q hasta que la serie sea estable. Después de construir el modelo y evaluarlo, se hará la predicción posterior, eliminando el paso de volver a hacer la diferencia. Sin embargo, la diferencia de precio de segundo orden no tiene sentido, por lo que ARMA es la mejor opción.

Selección del orden

A continuación, podemos seleccionar el orden directamente por el criterio de información, aquí lo intentamos con los diagramas termodinámicos de AIC y BIC.

En el [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Fuera [10]: Mejor parámetro AIC: (0, 1, 1) Mejor parámetro BIC: (0, 1, 1) Mejor parámetro de HQIC: (0, 1, 1) Mejor Param seleccionado: (0, 1, 1)

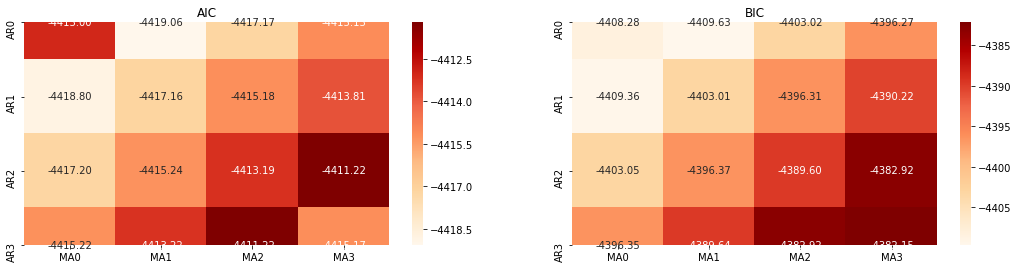
Es obvio que la combinación óptima de parámetros de primer orden para el precio logarítmico es (0,1,1), que es simple y sencilla. El log_return (tasa logarítmica de retorno) realiza la misma operación. El valor óptimo de AIC es (4,3), y el valor óptimo de BIC es (0,1). Así que la combinación óptima de parámetros para log_return (tasa logarítmica de retorno) es (0,1).

4-2 Modelado y coincidencia de ARMA

No se requieren coeficientes trimestrales, pero SARIMAX es más rico en atributos, por lo que se decidió elegir este modelo para el modelado y, por cierto, realizar un análisis descriptivo como sigue:

En [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Fuera [11]: Resultados del modelo del espacio estatal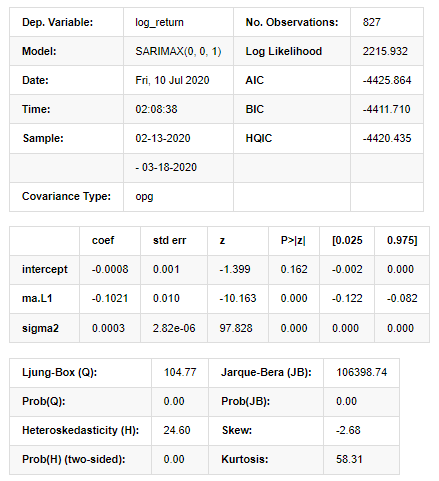

Advertencias: [1] Matriz de covarianza calculada utilizando el producto exterior de los gradientes (paso complejo). En [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Fuera[27]:

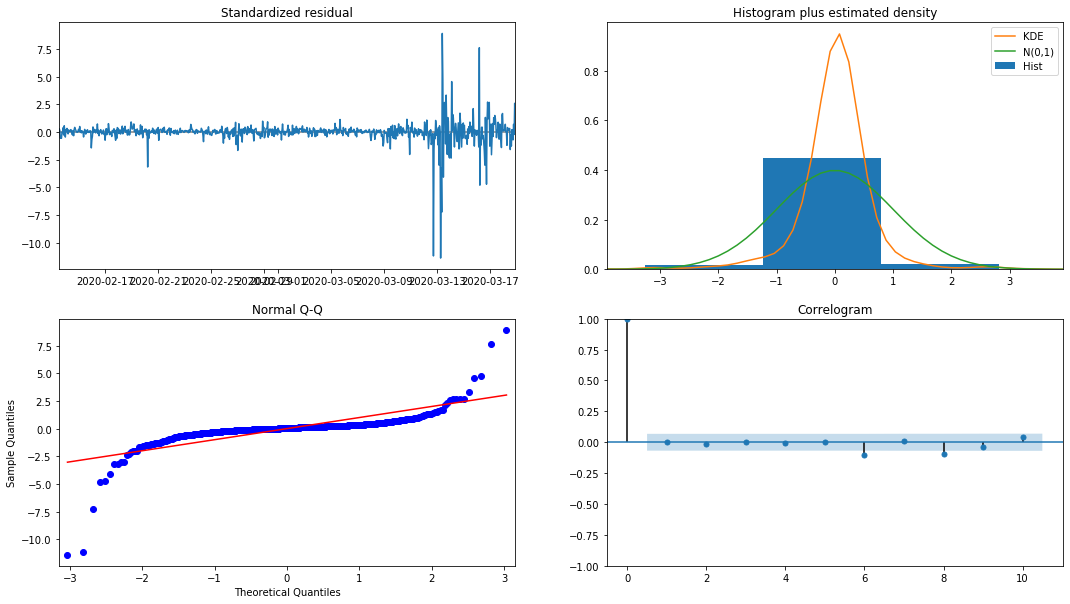
La densidad de probabilidad KDE en el histograma está lejos de la distribución normal N (0,1), lo que indica que el residuo no es una distribución normal.

Luego, dicho esto, todavía hay que probar si el modelo puede usarse.

4-3. Prueba del modelo

El efecto de coincidencia del residuo no es ideal, por lo que realizamos la prueba de Durbin Watson en él. La hipótesis original de la prueba es que la secuencia no tiene autocorrelación, y la secuencia de hipótesis alternativa es estacionaria. Además, si los valores P de las pruebas LB, JB y H son menores que el valor crítico del nivel de confianza del 0,05%, la hipótesis original será rechazada.

En [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Fuera [12]: En el ensayo de heteroskedasticidad de los residuos (breakvar): stat=24,598, p=0.000

Normalidad del ensayo de residuos (jarquebera): estat=106398.739, p=0.000

Correlación en serie de ensayo de los residuos (cuadro de luz): stat=104.767, p=0.000

Prueba de Durbin-Watson para los residuos: d=2,00 (Nota: 2 significa que no hay correlación en serie, 0=pos, 4=negativo)

Prueba para todas las raíces AR fuera del círculo unitario (>1): Verdadero

Prueba para todas las raíces MA fuera del círculo unitario (>1): Verdadero

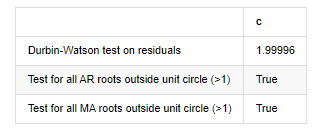
En [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Fuera[13]:

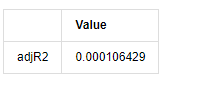
Si la estadística de la prueba de Durbin Watson es igual a 2, confirma que la serie no tiene correlación, y su valor estadístico se distribuye entre (0,4). Cerca de 0 significa que la correlación positiva es alta, mientras que cerca de 4 significa que la correlación negativa es alta. Aquí es aproximadamente igual a 2. El valor P de otras pruebas es lo suficientemente pequeño, la raíz característica de la unidad está fuera del círculo unitario, y cuanto mayor sea el valor del adjR2 modificado, mejor será. El resultado general de la medida no parece ser satisfactorio.

En [14]:

model_results.params

Fuera [1]: Interceptación -0.000817 el valor de las emisiones de gases de efecto invernadero sigma2 0,000275 D tipo: float64

En resumen, este parámetro de configuración de orden puede cumplir básicamente con los requisitos de modelado de series de tiempo y posterior modelado de volatilidad, pero el efecto de coincidencia es tal y cual.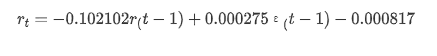

4-4. Pronóstico del modelo

A continuación, el modelo entrenado se empareja hacia adelante. statsmodels proporciona opciones estáticas y dinámicas para el emparejamiento y el pronóstico. La diferencia radica en si el valor de observación se utiliza en el siguiente paso del pronóstico, o el valor de predicción generado en el paso anterior se utiliza iterativamente. Los efectos de predicción de log_return (tasa logarítmica de retorno) son los siguientes:

En [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Fuera[37]:

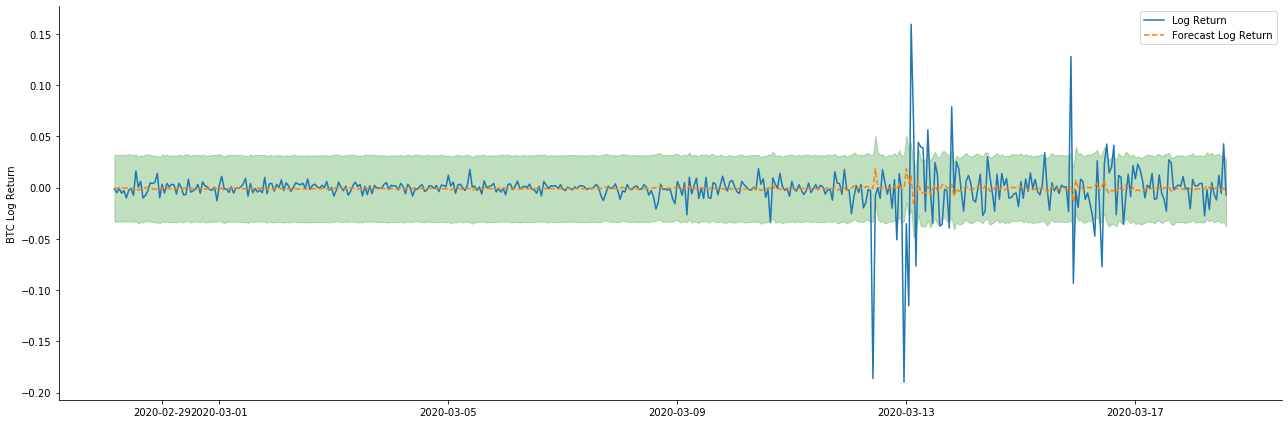
Se puede ver que el efecto de ajuste del modo estático en la muestra es excelente, los datos de la muestra pueden ser casi cubiertos por un intervalo de confianza del 95%, y el modo dinámico está un poco fuera de control.

Así que vamos a ver el efecto de coincidencia de datos en modo dinámico:

En [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Fuera[38]:

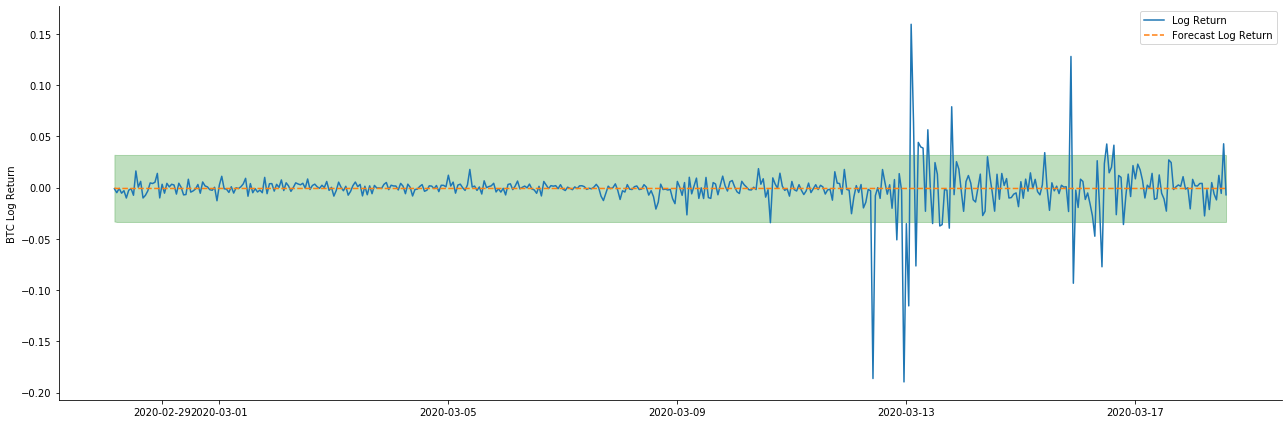
Se puede ver que el efecto de ajuste de los dos modelos en la muestra es excelente, y el valor medio puede ser casi cubierto por el intervalo de confianza del 95%, pero el modelo estático es obviamente más adecuado.

En [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Fuera[41]:

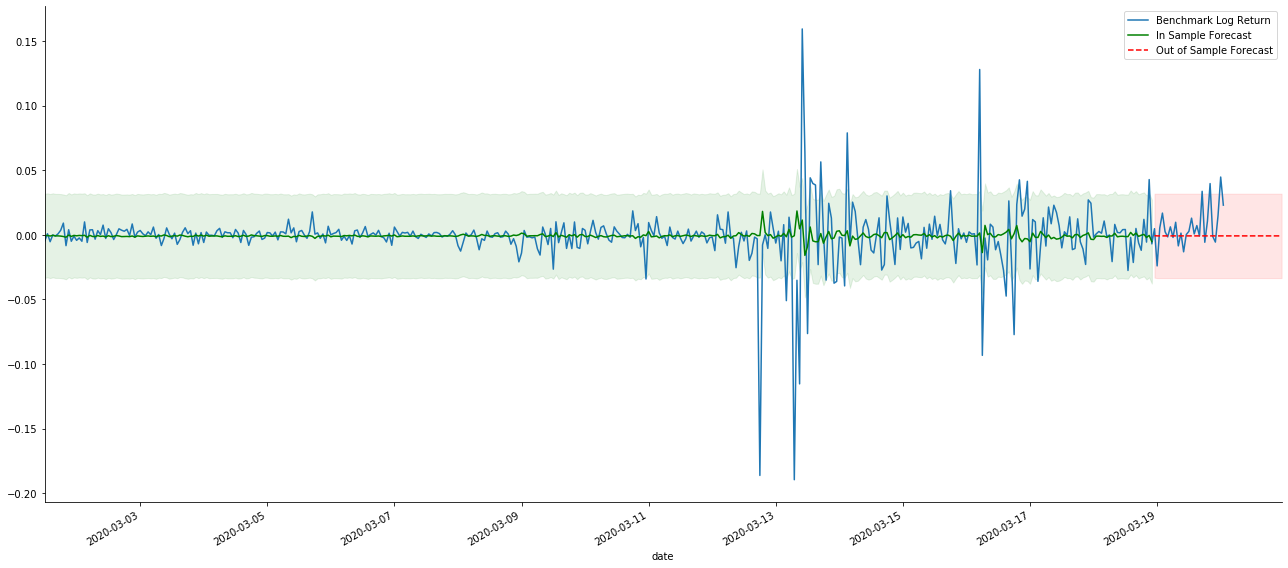
Debido a que la coincidencia de los datos en la muestra es una predicción progresiva, cuando la cantidad de información en la muestra es suficiente, el modelo estático es propenso a la coincidencia excesiva, mientras que el modelo dinámico carece de variables dependientes confiables, y el efecto se vuelve cada vez peor después de la iteración.

Si invertimos el pronóstico de tasa de rendimiento a log_price (precio logarítmico), la coincidencia se muestra en la figura siguiente:

En [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Fuera[42]:

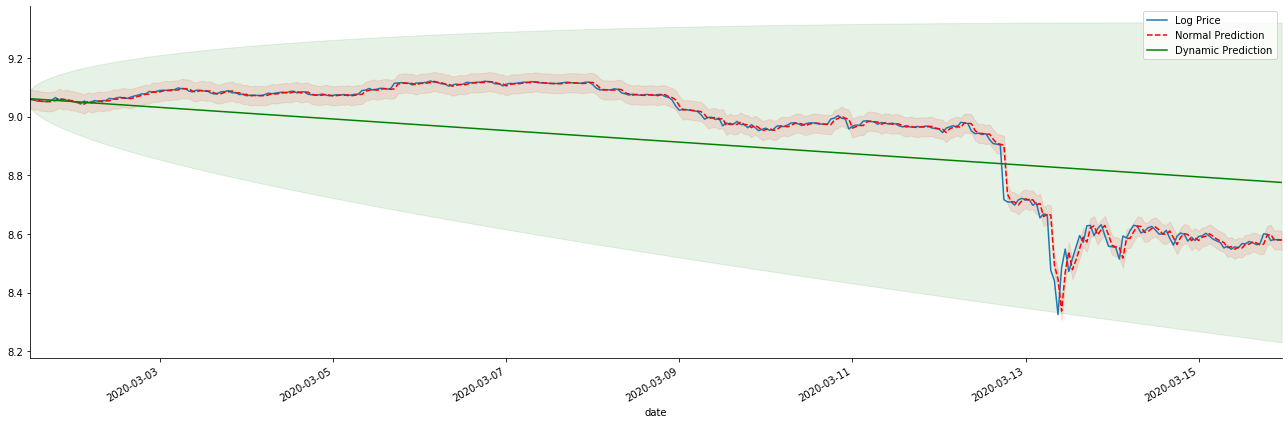
Es fácil ver las ventajas de coincidencia del modelo estático y la extrema diferencia entre el modelo dinámico y el modelo estático en la predicción a largo plazo. La línea punteada roja y el rango rosa... No se puede decir que la predicción de este modelo sea incorrecta. Después de todo, cubre la tendencia de la media móvil completamente, pero... ¿tiene sentido?

De hecho, el modelo ARMA en sí no está equivocado, porque el problema no es el modelo en sí, sino la lógica objetiva de las cosas mismas. El modelo de serie temporal solo se puede establecer sobre la base de la correlación entre las observaciones anteriores y posteriores. Por lo tanto, es imposible modelar la serie de ruido blanco. Por lo tanto, todo el trabajo anterior se basa en una suposición audaz de que la serie de tasa de retorno de BTC no puede ser independiente e idénticamente distribuida.

En general, las series de tasa de rendimiento son series de diferencia de martingala, lo que significa que la tasa de rendimiento es impredecible, y se mantiene la suposición de débil eficiencia del mercado correspondiente.

Sin embargo, la secuencia residual emparejada también es una secuencia de diferencia de martingala. La secuencia de diferencia de martingala puede no ser independiente e idénticamente distribuida, pero la varianza condicional puede depender del valor pasado, por lo que la autocorrelación de primer orden ha desaparecido, pero todavía hay autocorrelación de orden superior, que también es un requisito previo importante para que la volatilidad sea modelada y observada.

Si tal lógica es válida, entonces la premisa de construir varios modelos de volatilidad también es válida. Así que para una serie de tasas de rendimiento, si un mercado débilmente eficiente está satisfecho, entonces el valor medio debe ser difícil de predecir, pero la variación es predecible. Y el ARMA emparejado proporciona un punto de referencia de serie temporal de calidad justa, entonces la calidad también determina la calidad de la predicción de volatilidad.

Por último, evaluemos el efecto de la predicción de forma sencilla: con el error como punto de referencia de evaluación, los indicadores dentro y fuera de la muestra son:

En [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Fuera [1]: Error de la raíz media cuadrada (RMSE): 0,0184 Error de la raíz media cuadrada (RMSE): 0,0167 El error promedio en el porcentaje absoluto (MAPE): 2,25e+03 Percentaje medio de error absoluto (MAPE): 395

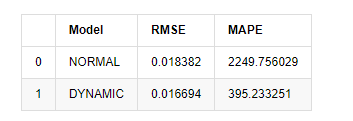
Se puede ver que el modelo estático es ligeramente mejor que el modelo dinámico en términos de coincidencia de error entre el valor predicho y el valor real. Se corresponde bien con la tasa de retorno logarítmico de Bitcoin, que está básicamente en línea con las expectativas. La predicción dinámica carece de información variable más precisa, y el error también se magnifica por iteración, por lo que el efecto de predicción es pobre.

En el [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Fuera [1]:

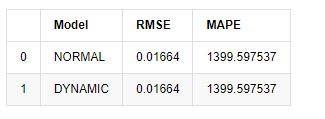
Dado que la próxima predicción fuera de la muestra depende de los resultados del paso anterior, solo el modelo dinámico es efectivo. Sin embargo, el defecto de error a largo plazo del modelo dinámico conduce a la capacidad de predicción insuficiente del modelo general, por lo que el siguiente paso se predice como máximo.

En resumen, el modelo estático del modelo ARMA es adecuado para coincidir con la tasa de retorno intra muestra de Bitcoin. La predicción a corto plazo de la tasa de retorno puede cubrir el intervalo de confianza de manera efectiva, pero la predicción a largo plazo es muy difícil, lo que satisface la débil efectividad del mercado.

5. Efecto ARCH

El efecto modelo ARCH es la correlación en serie de la secuencia de heteroscedasticidad condicional. La prueba de mezcla Ljung Box se utiliza para probar la correlación de la serie cuadrada residual para determinar si hay efecto ARCH. Si se aprueba la prueba de efecto ARCH, es decir, la serie tiene heteroscedasticidad, se puede llevar a cabo el siguiente paso del modelado GARCH para estimar la ecuación media y la ecuación de volatilidad conjuntamente. De lo contrario, el modelo necesita ser optimizado y reajustado, como procesamiento diferencial o serie recíproca.

Preparamos algunos conjuntos de datos y variables globales aquí:

En [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

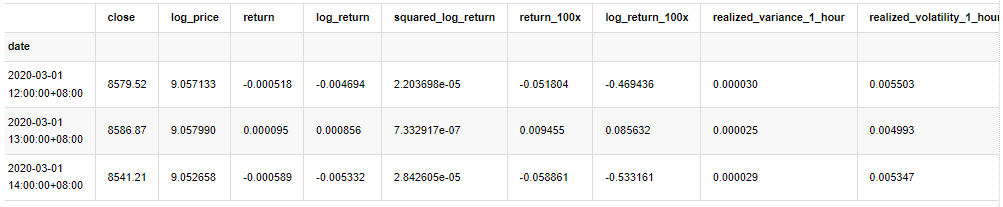
kline_test = kline_test[4:-2500]
kline_test.head(3)

Fuera[33]:

En [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Fuera[22]: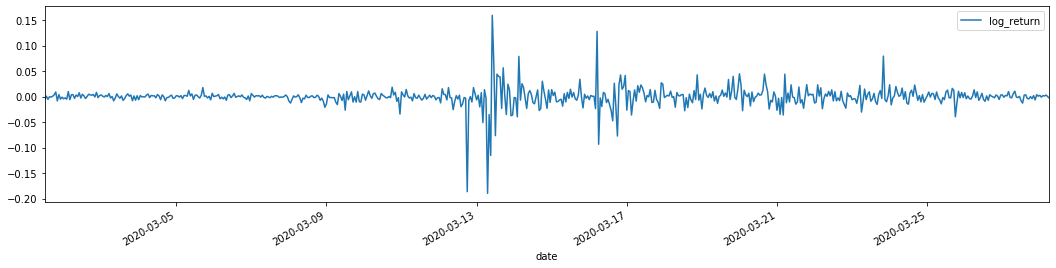 El objetivo de este proyecto es el desarrollo de un sistema de control de la calidad de los productos.

Las tasas de retorno logarítmicas se muestran arriba. A continuación, necesitamos probar el efecto ARCH de la muestra. Establecemos la serie residual dentro de la muestra basada en ARMA. Algunas series y la serie cuadrada de residual y residual se calculan primero:

En [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Fuera [1]:

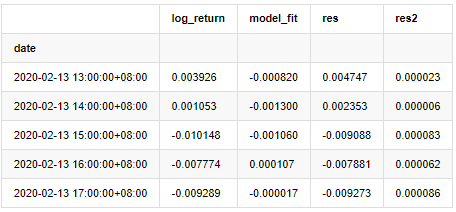
Se traza entonces la serie residual de la muestra

En [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Fuera[69]:

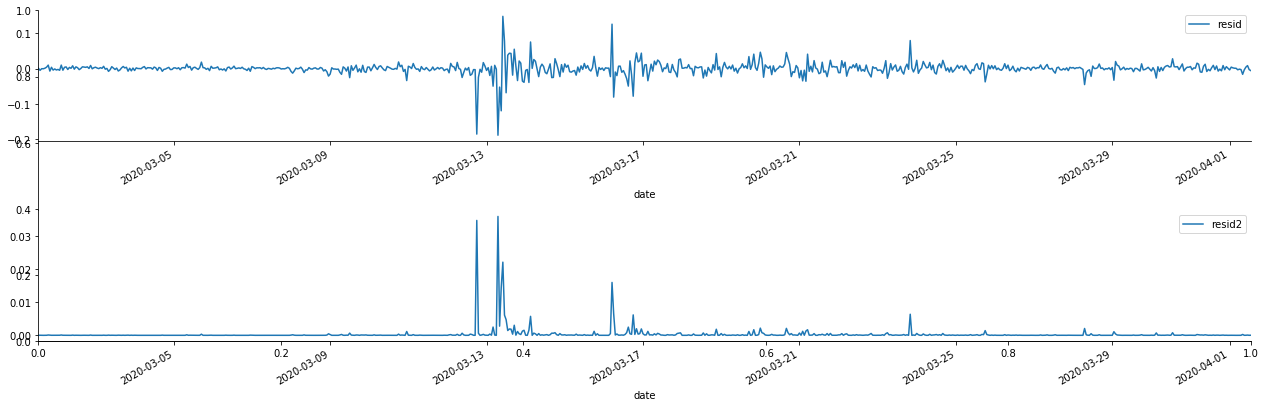
Se puede ver que la serie residual tiene características de agregación obvias, y se puede juzgar inicialmente que la serie tiene efecto ARCH. ACF también se toma para probar la autocorrelación de los residuos cuadrados, y los resultados son los siguientes.

En el [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Fuera de juego[70]:

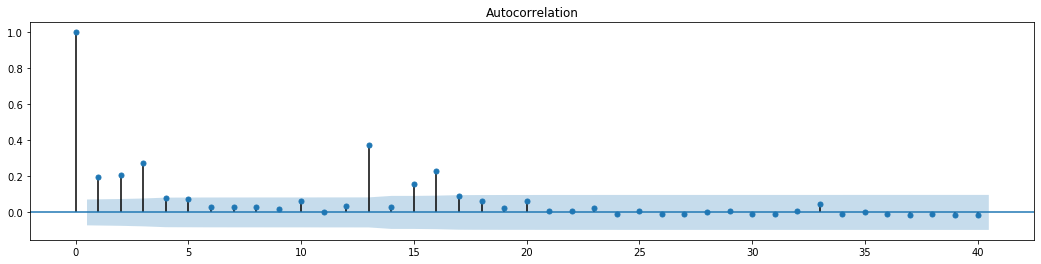
La suposición original para la prueba de mezcla de series es que la serie no tiene correlación. Se puede ver que los valores de P correspondientes de los primeros 20 órdenes de datos son menores que el valor crítico del nivel de confianza del 0,05%. Por lo tanto, se rechaza la suposición original, es decir, el residual de la serie tiene el efecto ARCH. El modelo de varianza se puede establecer a través del modelo de tipo ARCH para adaptarse a la heteroscedasticidad de la serie residual y predecir aún más la volatilidad.

6. Modelado de GARCH

Antes de realizar el modelado de GARCH, necesitamos tratar con la parte de la cola de grasa de la serie. Porque el término de error de la serie en la hipótesis necesita ajustarse a la distribución normal o distribución t, y hemos verificado previamente que la serie de rendimiento tiene una distribución de cola de grasa, por lo que necesitamos describir y complementar esta parte.

En el modelado de GARCH, el elemento de error proporciona las opciones de distribución normal, distribución t, distribución GED (distribución de error generalizada) y distribución t de estudiantes sesgados. De acuerdo con los criterios de AIC, usamos estimación de regresión conjunta de enumeración para comparar los resultados de todas las opciones y obtener el mejor grado de coincidencia de G

Relacionados

Más.