Mesurer le risque et le rendement - Une introduction à la théorie de Markowitz

La semaine dernière, lors de la présentationComment mesurer le risque de position - Introduction à la méthode VaRDans la première partie de ce chapitre, il a été mentionné que le risque d'un portefeuille n'est pas égal aux risques d'actifs individuels et est lié à leur corrélation de prix. En prenant deux actifs à titre d'exemple, si leur corrélation positive est très forte, c'est-à-dire qu'ils augmentent et diminuent ensemble, alors les investissements diversifiés ne réduiront pas le risque.

La théorie du portefeuille moderne (MPT), proposée par Harry Markowitz en 1952, est un cadre mathématique pour la sélection du portefeuille. Elle vise à maximiser les rendements attendus en choisissant différentes combinaisons d'actifs à risque tout en contrôlant le risque.

Le concept clé de la théorie de Markowitz

1. Taux de rendement attendu: Il s'agit du rendement que les investisseurs s'attendent à recevoir de la détention d'actifs ou d'un portefeuille d'investissement, généralement prévu sur la base des données historiques sur le rendement.

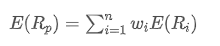
Où?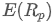est le rendement attendu du portefeuille,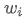est le poids du ième actif du portefeuille,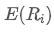est le rendement attendu de l'actif i.

2. Résultats de l'évaluation de la volatilité: Utilisé pour mesurer l'incertitude des rendements des investissements ou la volatilité des investissements.

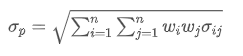
Où?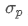représente le risque total du portefeuille,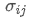est la covariance de l'actif i et de l'actif j, qui mesure la relation de variation de prix entre ces deux actifs.

3. Co-variance: mesure la relation mutuelle entre les variations de prix de deux actifs.

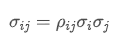
Où?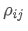est le coefficient de corrélation de l'actif i et de l'actif j,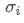et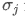sont respectivement les écarts types de l'actif i et de l'actif j.

4. Une frontière efficace: Dans le système de coordonnées risque-rendement, la frontière efficace est l'ensemble des portefeuilles d'investissement qui peuvent fournir le rendement maximal attendu à un niveau de risque donné.

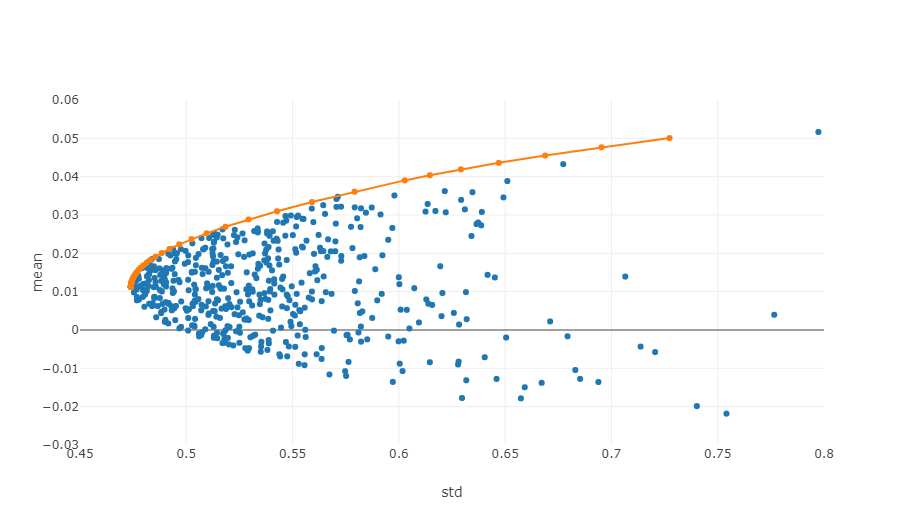
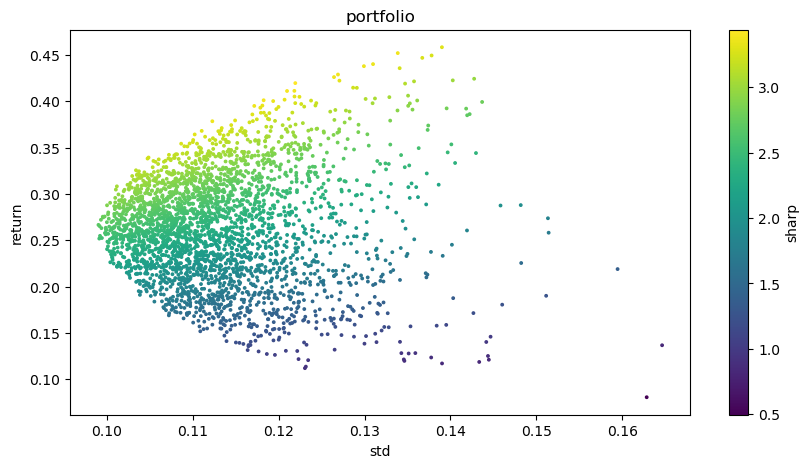
Le schéma ci-dessus est une illustration d'une frontière efficace, où chaque point représente un portefeuille d'investissement pondéré différent. L'axe x indique la volatilité, qui équivaut au niveau de risque, tandis que l'axe y indique le taux de rendement.

Dans le trading quantitatif et la gestion de portefeuille, l'application de ces principes nécessite une analyse statistique des données historiques et l'utilisation de modèles mathématiques pour estimer les rendements attendus, les écarts types et les covariances pour divers actifs.

Exemple de code Python pour trouver la combinaison optimale en utilisant la méthode de simulation

Le calcul du portefeuille optimal de Markowitz est un processus en plusieurs étapes, impliquant plusieurs étapes clés, telles que la préparation des données, la simulation du portefeuille et le calcul des indicateurs.https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Obtenir des données sur le marché:

À travers leget_dataCette fonction permet d'obtenir les données historiques des prix de la monnaie numérique sélectionnée, données nécessaires au calcul des rendements et des risques, qui sont utilisées pour construire des portefeuilles d'investissement et calculer les ratios Sharpe.

2. Calculer le taux de rendement et le risque:

Lecalculate_returns_riskCette fonction a été utilisée pour calculer les rendements annualisés et le risque annualisé (déviation type) pour chaque monnaie numérique.

3. Calculer le portefeuille optimal de Markowitz:

Lecalculate_optimal_portfolioDans chaque simulation, des pondérations d'actifs ont été générées au hasard, puis le rendement et le risque attendus du portefeuille ont été calculés sur la base de ces pondérations. En générant des combinaisons aléatoires avec des poids différents, il est possible d'explorer plusieurs portefeuilles d'investissement potentiels afin de trouver le meilleur.

L'objectif de l'ensemble du processus est de trouver le portefeuille d'investissement qui produit les meilleurs rendements attendus à un niveau de risque donné. En simulant plusieurs combinaisons possibles, les investisseurs peuvent mieux comprendre la performance de différentes configurations et choisir la combinaison qui convient le mieux à leurs objectifs d'investissement et à leur tolérance au risque. Cette méthode aide à optimiser les décisions d'investissement, rendant les investissements plus efficaces.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Résultat final de sortie: La combinaison optimale: Poids du BTCUSDT: 0,0721 Poids de l'ETHUSDT: 0,2704 Poids du BNBUSDT: 0,3646 Poids du LINKUSDT: 0,1892 Poids du BCHUSDT: 0,0829 Poids du LTCUSDT: 0,0209 Taux de rendement attendu: 0,4195 Risque attendu (déviation type): 0,1219 Le ratio de Sharpe: 3,4403