Bayes: déchiffrer le mystère de la probabilité, explorer la sagesse mathématique derrière la prise de décision
Auteur:FMZ~Lydia, Créé: 2023-11-27 11:55:42, Mis à jour: 2024-01-01 12:20:59
La statistique bayésienne est une discipline puissante dans le domaine des mathématiques, avec de larges applications dans de nombreux domaines, y compris la finance, la recherche médicale et les technologies de l'information.
Dans cet article, nous présenterons brièvement certains des principaux mathématiciens qui ont fondé ce domaine.
Avant Bayes
Pour mieux comprendre les statistiques bayésiennes, nous devons remonter au XVIIIe siècle et nous référer au mathématicien De Moivre et à son article
Dans son article, De Moivre a résolu de nombreux problèmes liés à la probabilité et au jeu à son époque.
L'une des questions les plus simples de son article était:
En lisant les problèmes décrits dans
Cela s'exprimerait aujourd'hui en termes mathématiques comme:
Formule
𝑃(𝑋|𝜃)
Cependant, si nous ne savons pas si la pièce est juste?𝜃 ?
Thomas Bayes et Richard Price
Près de cinquante ans plus tard, en 1763, un article intitulé
Dans les premières pages de ce document, il y a un article écrit par le mathématicien Richard Price qui résume un article de son ami Thomas Bayes écrit plusieurs années avant sa mort.
En fait, il a évoqué un problème spécifique:
En d'autres termes, après avoir observé un événement, nous déterminons quelle est la probabilité qu'un paramètre inconnuθC'est en fait l'un des premiers problèmes liés à l'inférence statistique dans l'histoire et il a donné naissance au terme inverse de probabilité.
Formule
𝑃( 𝜃 | 𝑋)
C'est bien sûr ce que nous appelons la distribution postérieure du théorème de Bayes
Pour une raison sans cause ni effet
Comprenant les motivations derrière la recherche de ces deux anciens ministres,Thomas BayesetRichard Price est là.Mais pour cela, nous devons temporairement mettre de côté quelques connaissances sur les statistiques.
Nous sommes au 18ème siècle où la probabilité devient un domaine de plus en plus intéressant pour les mathématiciens. Des mathématiciens comme de Moivre ou Bernoulli ont déjà montré que certains événements se produisent avec un certain degré de hasard, mais sont toujours régis par des règles fixes. Par exemple, si vous lancez un dé plusieurs fois, un sixième du temps, il tombera sur six. C'est comme s'il y avait une règle cachée qui détermine les chances du destin.
Imaginez que vous soyez un mathématicien et un croyant dévot vivant à cette époque.
C'était en effet la question posée par Bayes et Price eux-mêmes. Ils espéraient que leur solution s'appliquerait directement à prouver que le monde doit être le résultat de la sagesse et de l'intelligence; fournissant donc des preuves de l'existence de Dieu comme cause ultime - c'est-à-dire une cause sans causalité.
Laplace
Étonnamment, environ deux ans plus tard, en 1774, sans avoir lu le papier de Thomas Bayes, le mathématicien français Laplace a écrit un papier intitulé "Sur les causes des événements par probabilité des événements", qui traite des problèmes de probabilité inverse.
C'est ce que nous connaissons aujourd'hui comme le théorème de Bayes:
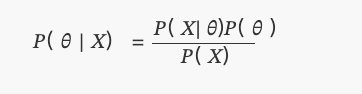
Où?P(θ)est une distribution uniforme.
Expérience de pièces
Nous allons amener les statistiques bayésiennes au présent en utilisant Python et PyMC bibliothèque, et mener une expérience simple.
Supposons qu'un ami vous donne une pièce et vous demande si vous pensez que c'est une pièce juste. Parce qu'il est pressé, il vous dit que vous ne pouvez lancer la pièce que 10 fois. Comme vous pouvez le voir, il y a un paramètre inconnupdans ce problème, qui est la probabilité de faire une tête en lançant des pièces, et nous voulons estimer la valeur la plus probable de lap.
(Remarque: Nous ne disons pas que le paramètrepest une variable aléatoire mais plutôt que ce paramètre est fixe; nous voulons savoir où il est le plus probable entre.)
Pour avoir des vues différentes sur ce problème, nous allons le résoudre sous deux croyances antérieures différentes:
-
- Vous n'avez aucune information préalable sur l'équité de la pièce, donc vous attribuez une probabilité égale à
pDans ce cas, nous utiliserons ce qu'on appelle un préalable non informatif parce que vous n'avez pas ajouté d'information à vos croyances.
- Vous n'avez aucune information préalable sur l'équité de la pièce, donc vous attribuez une probabilité égale à
-
- D'après votre expérience, vous savez que même si une pièce peut être injuste, il est difficile de la rendre extrêmement injuste.
pDans ce cas, nous utiliserons un préalable informatif.
- D'après votre expérience, vous savez que même si une pièce peut être injuste, il est difficile de la rendre extrêmement injuste.
Pour ces deux scénarios, nos croyances antérieures seront les suivantes:
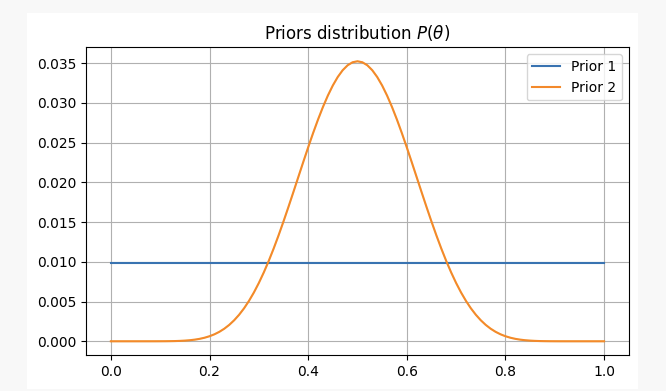
Après avoir lancé une pièce 10 fois, vous avez deux têtes.p?
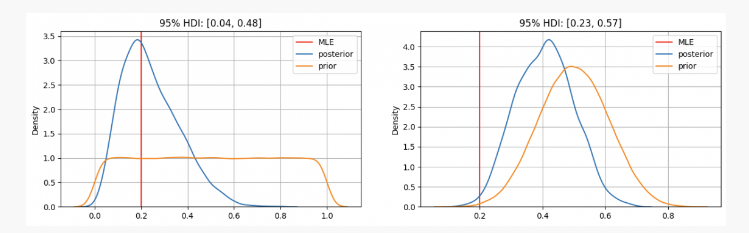
Comme vous pouvez le voir, dans le premier cas, notre distribution antérieure de paramètrepest concentrée à l'estimation de la probabilité maximale (MLE)p=0.2, qui est une méthode similaire à celle utilisée par l'école de fréquence. Le véritable paramètre inconnu sera dans l'intervalle de confiance de 95%, entre 0,04 et 0,48.
D'autre part, dans les cas où il existe une confiance élevée que le paramètrepDans ce cas, le véritable paramètre inconnu sera dans un intervalle de confiance de 95% entre 0,23 et 0,57.
Par conséquent, dans le premier scénario, vous diriez à votre ami avec certitude que cette pièce n'est pas juste, mais dans une autre situation, vous diriez qu'il est incertain qu'elle soit ou non juste.
Comme vous pouvez le voir, même face à des preuves identiques (deux têtes sur dix lancers), sous différentes croyances antérieures, les résultats peuvent varier considérablement; un avantage des statistiques bayésiennes par rapport aux méthodes traditionnelles réside ici: comme la méthodologie scientifique, elle nous permet de mettre à jour nos croyances en les combinant avec de nouvelles observations et preuves.
Résultats
Dans l'article d'aujourd'hui, nous avons vu les origines de la statistique bayésienne et ses principaux contributeurs.
- Quantification FMZ: analyse de l'exemple de conception des besoins courants sur le marché des crypto-monnaies (1)
- WexApp, la plateforme de démonstration de crypto-monnaie FMZ Quant, est récemment lancée.
- Explication détaillée de l'optimisation des paramètres de la stratégie de la grille de contrats perpétuels
- Apprenez à utiliser l'API étendue FMZ pour modifier les paramètres du bot
- Apprenez à modifier les paramètres du disque dur en masse à l'aide de l'API FMZ Extension
- Optimisation des paramètres stratégiques de la grille de contrats permanents
- Instructions pour l'installation de la passerelle IB Interactive Brokers dans Linux Bash
- Comment installer le GATEWAY pour les titres de pénétration sous Linux bash
- Qu'est-ce qui est le plus approprié pour la pêche au fond, la faible valeur marchande ou le faible prix?
- La valeur de marché est basse et le prix bas, lequel est le meilleur pour la traduction?
- Bayes: le mystère du déchiffrement de la probabilité, la recherche de la sagesse mathématique derrière les décisions
- Les avantages de l'utilisation de l'API étendue de FMZ pour une gestion efficace du contrôle de groupe dans le commerce quantitatif
- Résultats des prix après la cotation de la monnaie sur les contrats perpétuels
- Utilisation de l'API étendue FMZ pour une gestion efficace des clusters dans les transactions quantitatives
- Les prix après la mise en ligne de contrats permanents de devises
- La corrélation entre la hausse et la baisse des devises et le Bitcoin
- La correlation entre la chute des devises et le Bitcoin
- Une brève discussion sur l'équilibre des carnets de commandes dans les bourses centralisées
- Mesurer le risque et le rendement - Une introduction à la théorie de Markowitz
- Parler de l'équilibre du carnet de commandes des bourses centralisées