Nous avons discuté de l'optimisation des paramètres de plusieurs modèles de transactions programmatiques.

Nous avons discuté de l'optimisation des paramètres de plusieurs modèles de transactions programmatiques.

• Plateaux et îles paramétriques

Un principe important dans l'optimisation des paramètres est de rechercher des plateaux de paramètres plutôt que des îlots de paramètres. Le plateau de paramètres, en revanche, signifie qu'il existe une gamme de paramètres plus large, dans laquelle le modèle obtient de meilleurs résultats.

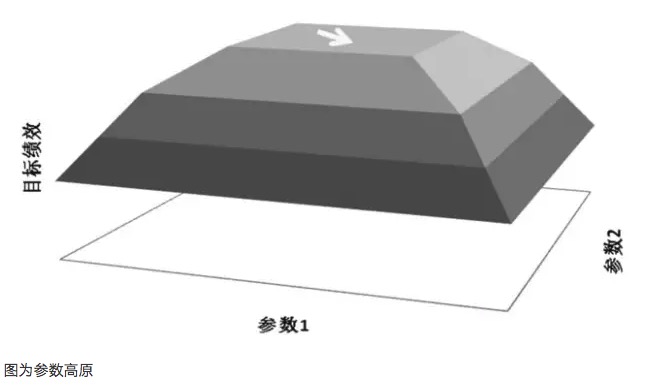
• Graphique pour les paramètres du plateau

  Prenons l'exemple de l'image de plateau paramétrique et de l'image d'isolement paramétrique. Supposons qu'un modèle de trading ait deux paramètres, les paramètres 1 et 2, et que les deux paramètres soient testés en trois dimensions. Une bonne distribution de paramètres devrait être celle de l'image de plateau paramétrique.

  

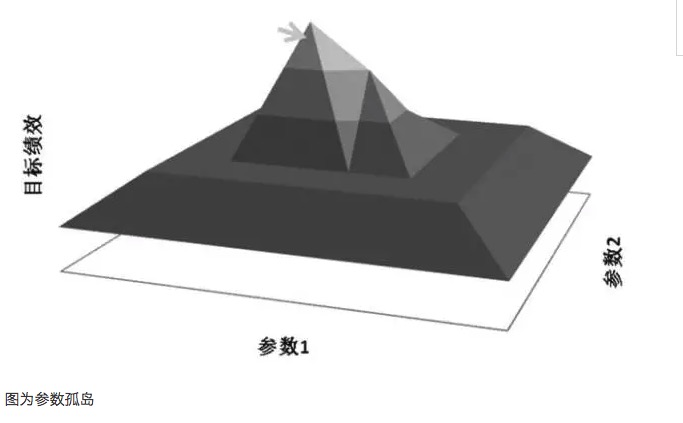
  En général, si le système de paramètres proches se comporte bien différemment du paramètre optimal, alors ce paramètre optimal peut être le résultat d'une sur-sommation, mathématiquement considérée comme une solution singulière plutôt qu'une solution à grande valeur recherchée. Mathématiquement, les singuliers sont instables et, dans des situations d'incertitude futures, le paramètre optimal peut devenir le paramètre le plus mauvais une fois que les caractéristiques du marché ont changé.

  L'hyperconformité est liée à l'échantillon sélectionné, si l'échantillon sélectionné ne peut pas représenter les caractéristiques globales du marché, et que les paramètres sont ajustés uniquement pour que les résultats du test atteignent la valeur attendue positive. Cette pratique est sans aucun doute une illusion de soi, et les paramètres obtenus sont des paramètres non valides d'hyperconformité. Par exemple, en analysant l'hyperconformité des paramètres, les modèles de négociation présentent un phénomène d'augmentation rapide des rendements aux valeurs 35 et 63 respectivement.

  La principale contradiction avec l'optimisation des paramètres est que les paramètres optimaux obtenus par l'optimisation des paramètres du modèle ne sont basés que sur des échantillons de données historiques qui ont déjà eu lieu, tandis que les marchés futurs sont dynamiques et présentent à la fois des similitudes et des variations par rapport aux marchés historiques. Les concepteurs de modèles peuvent trouver des paramètres pour lesquels les modèles se sont comportés le mieux dans l'histoire, mais ce paramètre n'est pas nécessairement le meilleur dans les applications réelles du modèle futur, et encore moins le meilleur dans l'histoire.

  En outre, les plateaux de paramètres et les îlots de paramètres ont souvent une relation plus grande avec le nombre de transactions. Si le nombre de transactions du modèle est faible, il est souvent possible de trouver un point de paramètre approprié pour que le modèle soit rentable sur ces plusieurs transactions, ce qui signifie que les gains du modèle après optimisation de paramètres reflètent une forte chance. Si le nombre de transactions du modèle est plus grand, la chance de gain du modèle diminue, ce qui reflète davantage l'inévitabilité et la régularité des gains.

• Comment optimiser les paramètres

  Après avoir compris le plateau des paramètres et l'isolement des paramètres, il est important d'optimiser les paramètres, en particulier lorsque plusieurs paramètres existent dans le modèle (ci-dessous les ensembles de paramètres), car il est fréquent que la prise de valeur d'un paramètre affecte la distribution des plateaux d'un autre paramètre.

  Une méthode est la convergence progressive; c'est-à-dire optimiser un paramètre séparément, puis fixer après avoir obtenu sa valeur optimale, puis optimiser l'autre paramètre, puis fixer après avoir obtenu sa valeur optimale. Ce cycle se poursuit jusqu'à ce que le résultat de l'optimisation ne change plus. Par exemple, dans un modèle de négociation croisée homogène, les deux paramètres indépendants sont respectivement la période courte N1 et la période longue N2.

  Une autre méthode consiste à utiliser une plate-forme de conception de logiciels programmatiques dotée de puissantes fonctionnalités de calcul, à calculer directement la distribution entre la fonction cible et l'ensemble des paramètres, puis à rechercher la distribution de la différence en plusieurs dimensions, à définir un seuil de différence dont la valeur absolue de la différence est inférieure à la limite de la valeur de la différence correspondant au volume en plusieurs dimensions le plus grand, le plus grand rayon de sphère interne en plusieurs dimensions, sélectionné comme paramètre le plus stable.

  En plus de l'optimisation des paramètres, la sélection des échantillons de données est également un facteur important. Les modèles qui suivent les tendances comme idées de trading fonctionnent mieux dans les marchés tendance et les stratégies qui achètent à bas prix comme idées de trading fonctionnent mieux dans les marchés oscillants. Par conséquent, lors de l'optimisation des paramètres, il est nécessaire d'éliminer correctement les marchés qui correspondent aux idées de trading pour prendre en compte les profits et d'ajouter des données sur les marchés qui ne correspondent pas aux idées de trading pour prendre en compte les pertes.

  À titre d'exemple, les futures boursières ont été un marché unilatérale depuis le début de l'introduction en 2010 et depuis la seconde moitié de 2014, date de l'apparition d'un marché extrême. Il ne fait aucun doute que tous les modèles de tendance donnent de bons résultats. Cependant, si nous intégrons ces données extrêmes dans l'échantillon pour optimiser les paramètres, les paramètres obtenus ne sont pas nécessairement les meilleurs.

  Par exemple, supposons qu'un modèle comporte deux paramètres: le paramètre A fonctionne très bien au moment de l'échantillonnage et fonctionne généralement au moment de l'échantillonnage; le paramètre B fonctionne moins bien au moment de l'échantillonnage et fonctionne mieux au moment de l'échantillonnage; la répartition entre les deux paramètres est uniforme. Même si le paramètre A fonctionne plus bien que le paramètre B pour les indicateurs globaux de l'échantillonnage, tels que le risque et le rendement, nous préférons le paramètre B, car le paramètre B est relativement plus stable et n'est pas dépendant d'un échantillon spécifique.

  En résumé, lors de la construction d'un modèle de négociation programmatique, il est possible d'optimiser le modèle par paramètres afin de le rendre plus adapté aux fluctuations des prix et d'améliorer le rendement de l'investissement; d'autre part, il est nécessaire d'éviter une adaptation excessive à l'optimisation des paramètres, ce qui réduit considérablement la pertinence du modèle pour les changements de marché.

Traduit de négociant programmé