Stratégie de trading haute fréquence du carnet d’ordres basée sur l’apprentissage automatique

• ### Les théories

Le mécanisme de négociation du marché des valeurs mobilières peut être divisé en deux catégories: les marchés à ordre et les marchés à ordre. Le premier repose sur le fait d’être un marchand de marché pour fournir la liquidité. Le second repose sur le fait d’offrir la liquidité par le biais d’une liste de prix limite.

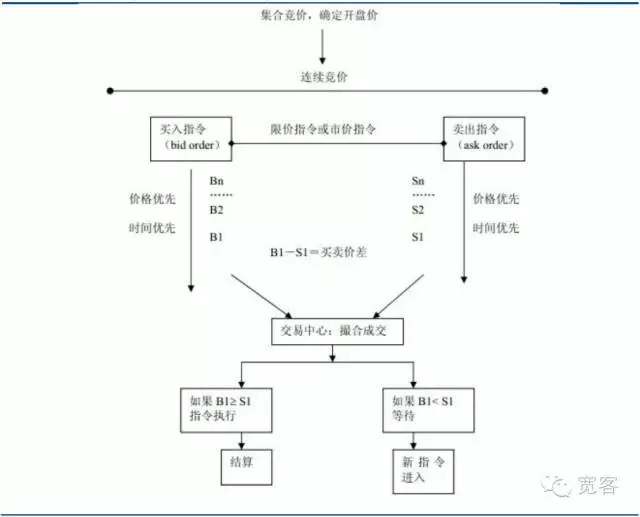Graphique 1 Le diagramme du marché axé sur les commandes

• (i) Résumé du carnet de commandes à prix limité

  La théorie de la microstructure du marché s’appuie sur la théorie des prix et de la théorie des fournisseurs de la microeconomie, et dans son analyse des processus et des causes de la formation des prix des transactions d’actifs financiers, elle utilise diverses théories et méthodes telles que l’équilibre général, l’équilibre local, les gains marginaux, les coûts marginaux, la continuité du marché, la théorie des stocks, la théorie des jeux et l’économie de l’information.

  D’après les progrès de la recherche à l’étranger, le domaine de la microstructure du marché est représenté par O’Hara. La plupart des théories sont basées sur des marchés marchands (c’est-à-dire des marchés axés sur les offres), tels que les modèles d’inventaire et les modèles d’information.

  Les marchés de valeurs mobilières et les marchés à terme domestiques sont des marchés à ordre. Voici une capture d’écran du carnet d’ordres de niveau_1 pour le contrat à terme sur indices boursiers IF1312. Il n’y a pas beaucoup d’informations directement obtenues à partir de ce qui précède. Les informations de base comprennent un prix d’achat, un prix de vente, un montant d’achat et un montant de vente.

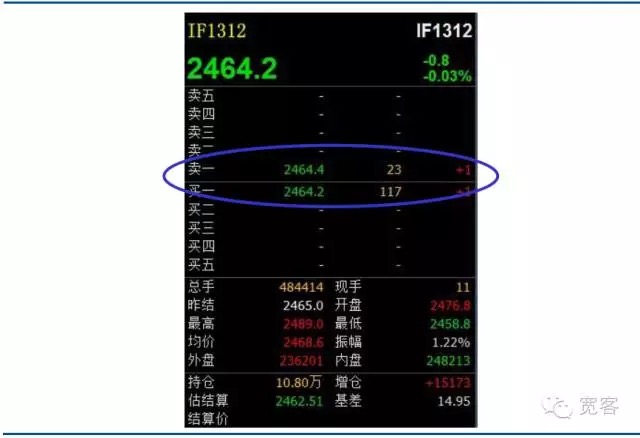  Graphique 2 Livret de commande de niveau 1 pour les contrats de force majeure sur indices boursiers à terme

• (ii) Les progrès réalisés dans la recherche sur les transactions à haute fréquence dans les carnets de commandes

  La modélisation dynamique des carnets de commandes se fait principalement par deux méthodes, l’une est la méthode classique de l’économie quantique et l’autre est la méthode de l’apprentissage automatique. La méthode d’économie quantique est une méthode de recherche classique et dominante, comme la décomposition du MRR pour l’analyse des écarts de prix, la décomposition de Huang et Stoll, la modélisation de l’ACD pour la durée des commandes et la modélisation logistique pour la prévision des prix.

  La recherche académique sur l’apprentissage automatique dans le domaine de la finance est également très active, par exemple dans le domaine de la prévision des tendances de haute fréquence KOSPI200 index data using learning classifiers en 2012. C’est une idée de recherche courante qui utilise les indicateurs courants de l’analyse technique (MA, EMA, RSI, etc.) pour faire des prévisions de marché.

• Application de l’apprentissage automatique dans les transactions à haute fréquence dans les carnets de commandes

  • #### a) Le schéma de l’architecture du système

  Le schéma ci-dessous est une architecture systémique d’une stratégie de trading typique de l’apprentissage automatique, comprenant les données du carnet de commandes, la découverte de fonctionnalités, la construction et la validation de modèles et les opportunités de trading. Il convient de noter que le processus de trading est déclenché par des événements de tendance, l’arrivée d’un tick de tendance étant l’un de ces événements.

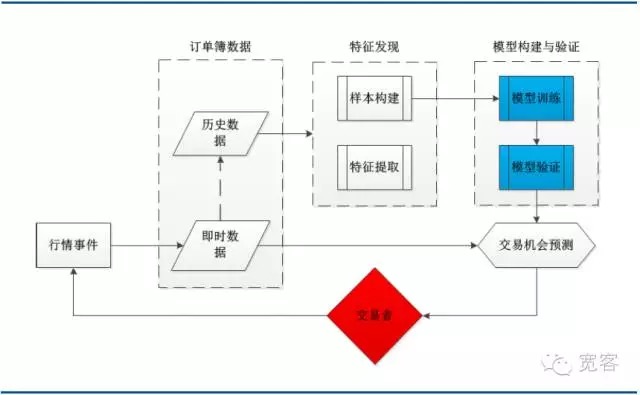  Figure 3 Diagramme de l’architecture du système pour la modélisation de la caisse de commandes basée sur l’apprentissage automatique

  • #### (ii) Définition du vecteur de support

  Dans les années 1970, Vapnik et d’autres ont commencé à construire un système théorique relativement complet de théories de l’apprentissage statistique (SLT, Statistical Learning Theory), qui a été utilisé pour étudier les lois statistiques et la nature des méthodes d’apprentissage dans des situations limitées de l’échantillon. Il a créé un bon cadre théorique pour les problèmes d’apprentissage de la machine dans des échantillons limités, et a mieux résolu les problèmes pratiques tels que le petit échantillon, la non-linéarité, la haute dimension et les extrêmes locaux.

  SVM est une évolution de l’hyperplan de classification optimale pour les cas de division linéaire. Pour les problèmes de classification de deux classes, on définit l’ensemble de l’échantillon d’entraînement comme suit: ((xi,yi), i = 1,2 … l, l est le nombre d’échantillons d’entraînement, xi est l’échantillon d’entraînement, yi appartient à {-1 + 1} est le marqueur de classe d’entrée de l’échantillon xi (expected output). Le point de départ de l’algorithme SVM est de trouver l’hyperplan de classification optimale.

  L’hyperplanche de classification optimale permet non seulement de séparer correctement tous les échantillons (le score d’erreur d’entraînement est de 0), mais permet également de maximiser la marge (la marge) entre les deux catégories, définie comme la somme de la distance minimale entre l’ensemble de données d’entraînement et l’hyperplanche de classification. L’hyperplanche de classification optimale signifie que l’erreur de classification moyenne des données de test est minimale.

  Si un superplan existe dans un espace vectoriel en d dimensions:

  F(x)=w*x+b=0

  Le superplan qui peut séparer ces deux types de données est appelé une interface.*x est la somme des deux vecteurs w et x dans un espace vectoriel d dimension.

  Si l’interface est:

  w*x+b=0

  L’interface qui permet d’obtenir la plus grande distance (la marge) entre les deux échantillons les plus proches de l’interface est appelée l’interface optimale.

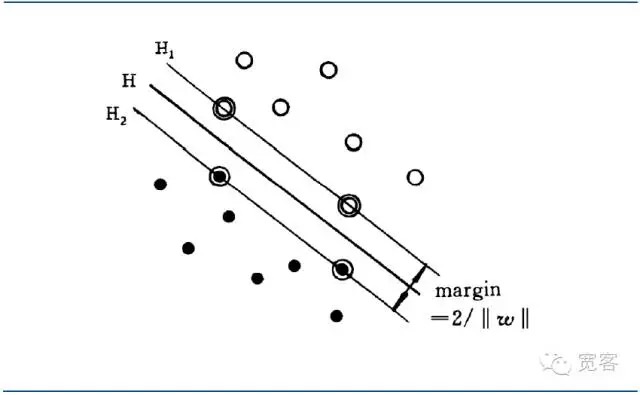  Figure 4 Diagramme de l’interface optimale de la classe 2 du SVM

  L’uniformisation de l’équation d’interface optimale permet de rendre la distance entre deux types d’échantillons

  

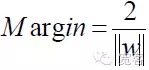
  Donc, pour n’importe quel échantillon, il y a

  

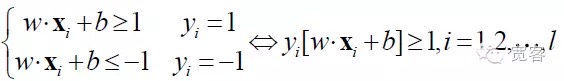
  Pour obtenir l’interface optimale, en plus de satisfaire à la formule ci-dessus, il faut aussi la minimiser.

  Le modèle mathématique du problème SVM est donc:

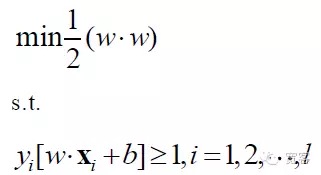
  La SVM est finalement devenue un problème de planification d’optimisation, et la recherche académique se concentre principalement sur la résolution rapide, la diffusion vers les classes multiples, l’application de problèmes pratiques, etc.

  Le SVM a été initialement proposé pour les problèmes de classification binaire, mais il a été étendu aux problèmes multiclassés en fonction des exigences des applications actuelles. Les algorithmes multiclassés existants comprennent le codage par paire, le codage par paire, le codage de correction d’erreur, le DAG-SVM et le classificateur SVM Mult i-class.

  • #### (iii) Extraction des indices du carnet de commandes

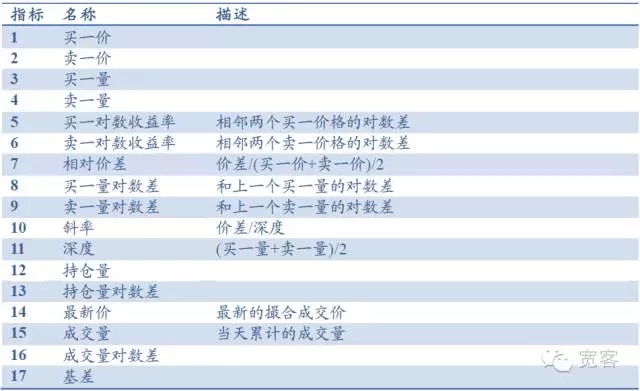
  Le carnet d’ordres est composé principalement d’indicateurs de base tels que le prix d’achat, le prix de vente, le montant d’achat et le montant d’achat. Il peut être dérivé de profondeur, de pente, d’écart de prix relatif, d’autres indicateurs incluent le volume de la position, le volume de transaction, l’écart de base, etc.

  Tableau 1 Base d’indicateurs basée sur le carnet de commandes du marché Level

  

  • #### (iv) Caractéristiques dynamiques du carnet de commandes et opportunités de négociation

  Du point de vue de la microscopie du marché, il existe deux méthodes de mesure de la dynamique des prix à court terme, l’une est la dynamique des prix moyens et l’autre est la dynamique des prix moyens croisés. Le présent article choisit une dynamique des prix moyens plus simple et plus intuitive.

  

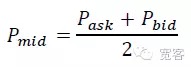
  Selon le carnet d’ordres, la taille de la variation de la valeur médiane ΔP dans Δt est divisée en trois catégories:

  Le graphique ci-dessous montre la distribution de la dynamique médiane du contrat IF1311 le 29 octobre, avec 32 400 ticks par jour.

  Dans le cas où Δt = 1 tick, la variation moyenne des valeurs absolues est de 0,2 environ 6000 fois, la variation absolue est de 0,4 environ 1500 fois, la variation absolue est de 0,6 environ 150 fois, la variation absolue est de 0,8 plus de 50 fois, la variation absolue est supérieure à 1 environ 10 fois.

  Dans le cas de Δt=2tick, la variation moyenne des valeurs absolues est de 0,2 environ 7000 fois, la variation absolue est de 0,4 environ 3000 fois, la variation absolue est de 0,6 environ 550 fois, la variation absolue est de 0,8 environ 205 fois, la variation absolue est supérieure ou égale à 1 environ 10 fois.

  Nous considérons que la variation de la valeur absolue est supérieure ou égale à 0,4 pour les opportunités potentielles. Dans le cas de Δt = 1 tick, il y a environ 1700 opportunités par jour; dans le cas de Δt = 2 tick, il y a environ 4000 opportunités par jour.

  

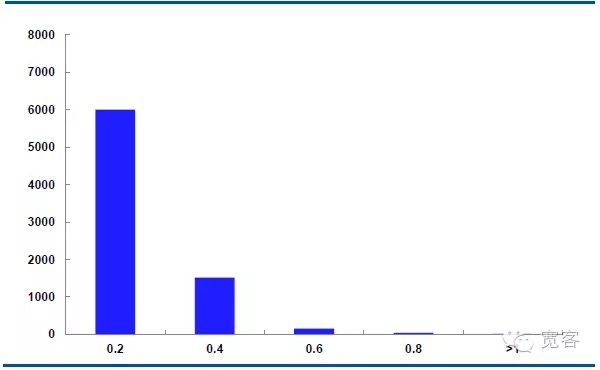
  Figure 5 Distribution de la variation du cours moyen du 29 octobre (Δt=1 tick)

  

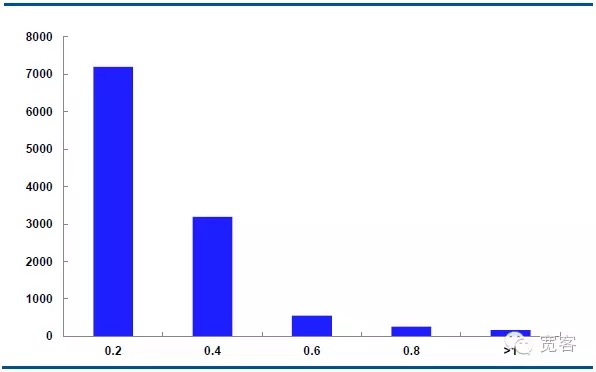
  Figure 6 Distribution de la variation du cours moyen du 29 octobre (Δt=2 tick)

• Troisièmement, la stratégie est vérifiée.

Comme les modèles SVM ont une complexité de formation plus élevée et une durée de formation plus longue dans les cas de grands échantillons, nous avons choisi des données de cas historiques avec une période de temps relativement courte, en prenant l’exemple des données de cas de niveau_1 du contrat IF1311 en octobre, pour valider l’efficacité du modèle.

• (i) Tests d’efficacité des modèles

  Cycle de données: données sur le marché des contrats IF1311 pour le mois d’octobre;

  La valeur de Δt: plus Δt est petit, plus les exigences de détails de la transaction sont élevées. Lorsque Δt = 1 tick, il est difficile d’obtenir des bénéfices dans la transaction réelle. Pour comparer l’efficacité du modèle, nous valorisons respectivement 1 tick, 2 tick et 3 tick;

  Indicateurs d’évaluation du modèle: précision des échantillons, précision des tests, temps de prévision. 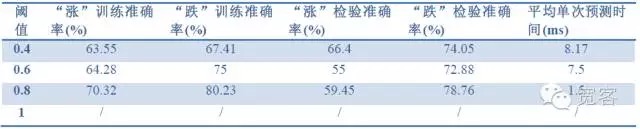Tableau 2 Prédire l’effet d’une tick avec les données d’une tick

  Tableau 3 Prédire l’effet d’un tick2 avec les données de tick1

  Tableau 4 Prédire l’effet de 2 ticks avec des données de 2 ticks

  Les données des trois tableaux ci-dessus nous permettent de tirer les conclusions suivantes: La précision maximale est d’environ 70% et la précision de 60% peut être convertie en stratégie de trading.

• (ii) Des gains simulés par la stratégie

  Prenons le 31 octobre, par exemple, nous avons effectué une transaction simulée, les commissions pour les transactions à terme sur indices boursiers de l’établissement sont généralement les commissions pour les transactions à terme sur indices boursiers de l’établissement sont généralement de 0,²⁶⁄₁₀₀₀₀, nous supposons que le nombre de transactions n’a pas de limite de liquidation, supposons que chaque transaction a un décalage unilatéral de 0,2 points, chaque commande est de 1 main.

  Tableau 5 Stratégies simulées au 31 octobre

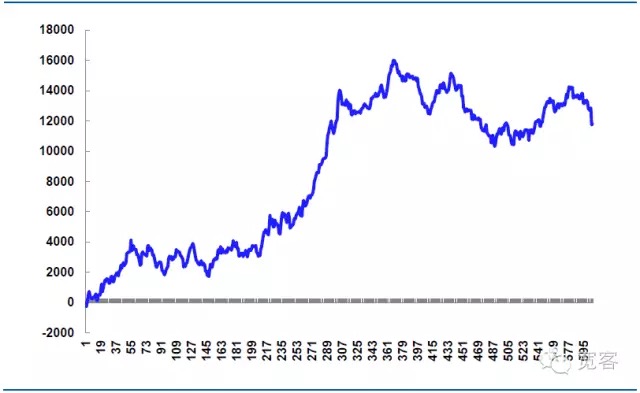
  Le nombre de transactions a été de 605 transactions en une journée, 339 transactions ont été réalisées, avec un taux de victoire de 56% et un bénéfice net de 11814,99 yuans.

  Le cours de dépréciation théorique est de 14520 yuans, ce qui est en partie la clé de la bataille de stratégie. Si les détails de commande sont contrôlés plus finement, le cours de dépréciation peut être réduit et le bénéfice net augmenté. Si les détails de commande sont mal contrôlés ou si le marché fluctue anormalement, le cours de dépréciation sera plus important et le bénéfice net diminué.

  Figure 7: Résultats du simulateur au 31 octobre

Déclaration de l’auteur: Cet article a été rédigé par l’auteur de l’article publié sur le site de l’association, et a été reproduit à partir d’une autre source.