Les mathématiques et le jeu

• Nous savons que le jeu de hasard est un jeu de probabilité, et ce sont des résultats de jeu étranges qui ont suscité l’intérêt des mathématiciens Pascal et Fermat, qui ont échangé des lettres pour proposer des principes de la théorie des probabilités, créant ainsi la théorie de la probabilité.

• 1 Le jeu parfait

Il y a un match entre les Lakers et les Cowboys de la NBA, et les deux équipes ont des fans fidèles, on les appelle les Cowboys et les Cowboys. Les fans pensent bien sûr que leur équipe est plus susceptible de gagner, alors ils sont prêts à parier avec vous. Supposons que les Cowboys pensent que les Lakers ont une probabilité de gagner de p, et les Cowboys pensent que les Cowboys ont une probabilité de gagner de q, p et q.

La méthode est la suivante: nous jouons le même pari que les papillons de l’ethnie des Octopus et les papillons de l’ethnie des Scorpions, si nous gagnons nous gagnons y et si nous perdons nous perdons x, tant que y>x nous sommes gagnants. Et x et y n’ont qu’à satisfaire aux deux inégalités suivantes, les gains escomptés des papillons de l’ethnie des Octopus et des papillons de l’ethnie des Scorpions sont positifs, et nous parions:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Si p > q, la solution est la partie bleue de la figure suivante:

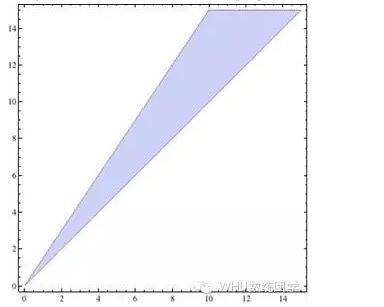
Le problème semble parfaitement résolu, mais il y a une autre question, et je suis sûr que le lecteur découvrira rapidement son absurdité: que ce soit les chiens de la tribu des Yang ou les chiens de la tribu des Yang, leurs attentes de rendement sont positives, c’est-à-dire qu’à long terme, ils gagnent de l’argent, alors que nous ne faisons pas de profits, alors d’où vient tout cet argent, et comment est-ce que tout le monde peut gagner de l’argent ?

• ### La fraude à deux ou trois cartes

C’est une autre astuce de mise en jeu, on commence avec trois cartes, la première est noire face à face, la deuxième est rouge face à face, la troisième est noire face à face, la troisième est rouge face à face. Puis on met les cartes dans une boîte, on les secoue et on demande à l’adversaire de tirer une carte de la même couleur que la face.

En fait, la probabilité de gagner n’est pas ¹⁄₂, mais ²⁄₃, et l’aspect le plus déroutant de ce jeu est la double face des cartes. Le joueur ne tire pas 3 cartes, mais 6 cartes: 3 faces noires, 3 faces rouges. Nous numérotons ces 6 faces A, B, C, D, E, F:

Lorsque le joueur tire sur la face noire, il y a trois possibilités A, C et D, dont les faces arrière sont respectivement D, F et A, avec le noir représentant les ²⁄₃ des cas.

Le problème a été posé en 1889 par le mathématicien français Joseph Louis François Bertrand, et il est connu sous le nom de paradoxe de la boîte de Bertrand. En 1950, le mathématicien américain Warren Weaver a introduit le jeu de cartes ci-dessus, que Martin Gardner a appelé la fraude à trois cartes.

• ### 3 Une noix de muscade aussi inhabituelle

Parfois, au début du jeu, nous laissons tomber l’eau, laissons d’abord quelqu’un d’autre gagner un peu d’argent, lançons un long filet pour attraper un gros poisson, et finalement un filet est terminé. Voici un excellent exemple. Quatre personnes jouent au bridge, je dis d’abord: venez jouer un craps, j’ai maintenant un A, devinez si j’ai plus d’A? Dans ce cas, vous risquez de perdre, alors vous désignez en tête un A de couleur, par exemple, un A de noix de coco, et quand un certain tour a attrapé un A de noix de coco, l’occasion est venue: allez jouer un autre craps, j’ai maintenant un A de noix de coco, devinez si je n’ai plus d’A de noix de coco.

Beaucoup de gens pensent que deux oranges ne sont pas si différentes que ça, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux, qu’il n’y a pas de différence entre les deux.

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

Mais après la pose de la première couche, la volonté de parier a été mobilisée, en voyant que la deuxième couche n’était pas juste un changement de vêtements, ils ont misé plus fort, puis ils ont dit que je n’avais pas plus de A, et nous sommes en plein milieu.

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

D’après l’équipe statistique de la WHU