Prédire le prix du Bitcoin en temps réel à l'aide du framework LSTM

Attention: ce cas est uniquement à des fins d'étude et de recherche et ne constitue pas une recommandation d'investissement.

Les données de prix du bitcoin sont basées sur des séquences chronologiques, de sorte que les prévisions de prix du bitcoin sont généralement réalisées en utilisant le modèle LSTM.

La mémoire à court et long terme (LSTM) est un modèle d'apprentissage en profondeur particulièrement adapté aux données de séquence temporelle (ou à celles qui ont une séquence temporelle / spatiale / structurelle, comme les films, les phrases, etc.) et est le modèle idéal pour prédire l'orientation des prix des crypto-monnaies.

Cet article est principalement consacré à la synthèse de données à l'aide du LSTM afin de prédire le prix futur du Bitcoin.

Importer les bibliothèques à utiliser

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Analyse des données

Le chargement des données

Lire les données quotidiennes sur les transactions en BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

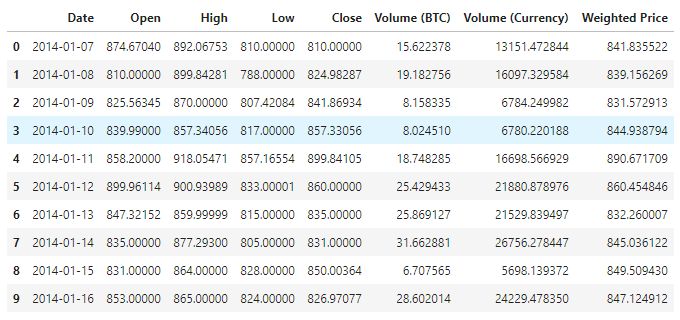
Les données sont disponibles pour un total de 1380 articles, composés des colonnes Date, Open, High, Low, Close, Volume (BTC), Volume (Currency) et Weighted Price.

data.info()

Voir les 10 premières lignes

data.head(10)

Visualisation des données

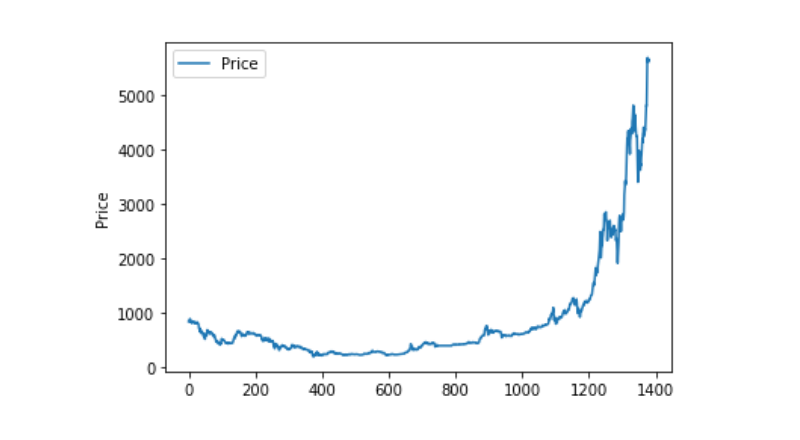
Utiliser matplotlib pour tracer le prix pondéré pour voir la distribution et la tendance des données. Dans le graphique, nous avons trouvé une partie de données 0 et nous devons vérifier si les données ci-dessous sont anormales.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Traitement des données exceptionnelles

On peut voir que dans nos données il n'y a pas de données nan.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Si vous regardez la base de données 0 et que vous voyez qu'il y a une valeur 0 dans notre base de données, nous devons traiter cette valeur 0.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

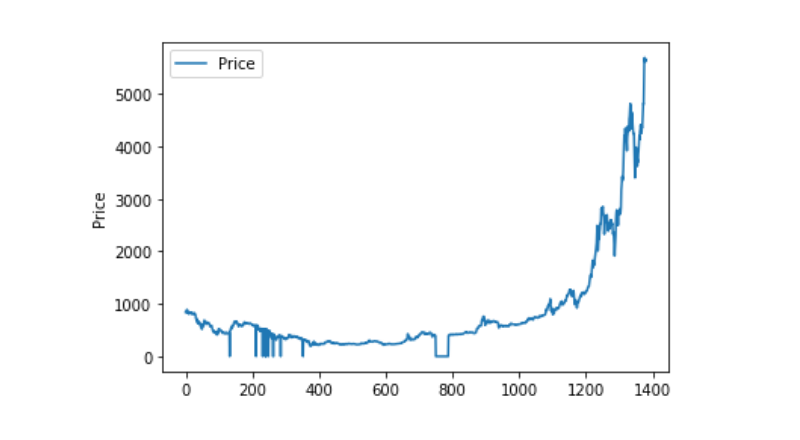
Si vous regardez la distribution et la tendance des données, la courbe est déjà très continue.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Séparation des ensembles de données de formation et de test

Unifier les données à 0 à 1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Divisez les ensembles de données de test et de formation par 2:8.

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Créer des ensembles de données d'entraînement et de test pour une fenêtre de 1 jour pour créer nos ensembles de données d'entraînement et de test.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Définir et former les modèles

Cette fois, nous avons utilisé un modèle simple, dont la structure est la suivante: 1. LSTM2.

La dimension d'entrée de la forme d'entrée de LSTM est la taille du lot, les étapes de temps, les fonctionnalités. La valeur de la fenêtre de temps est l'intervalle de la fenêtre de temps au moment de l'entrée de données, nous utilisons 1 jour comme fenêtre de temps, et nos données sont des données de jour, donc ici nos étapes de temps sont de 1.

La mémoire à court terme (LSTM) est un type particulier de RNN qui est principalement utilisé pour résoudre les problèmes de disparition de gradient et d'explosion de gradient lors d'un entraînement à longue séquence.

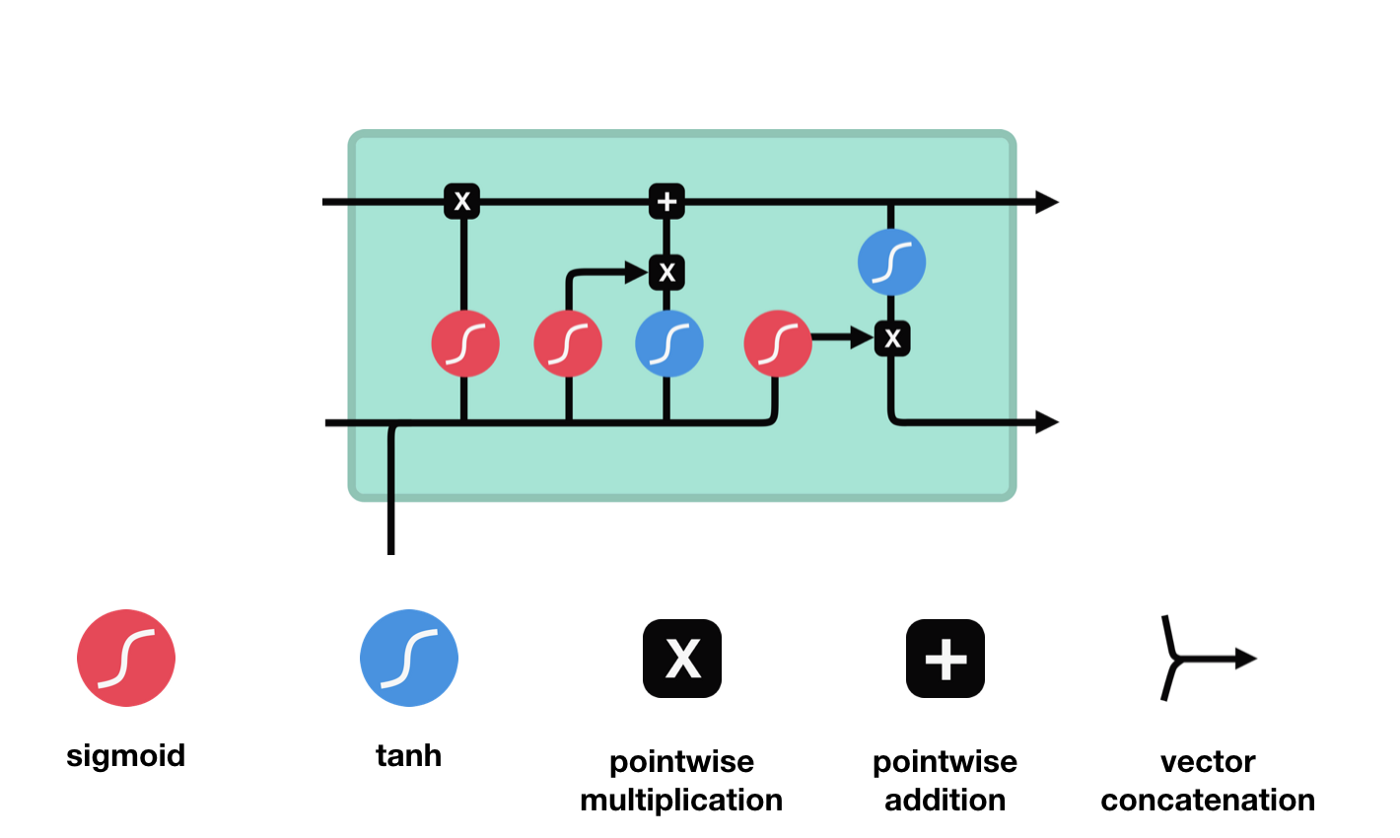
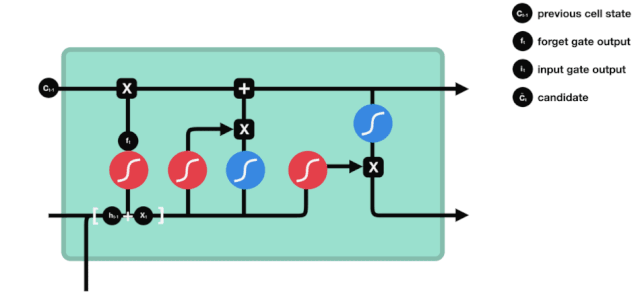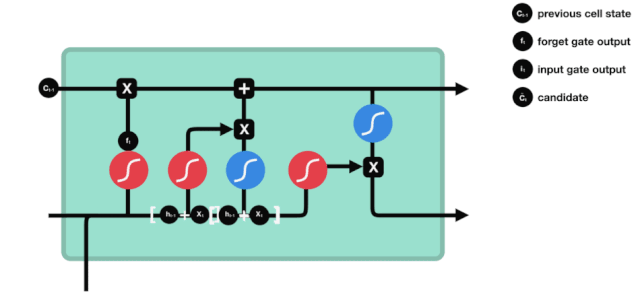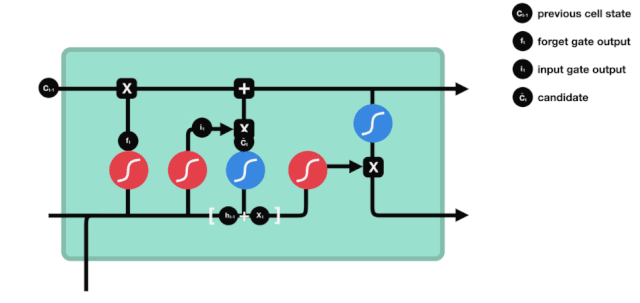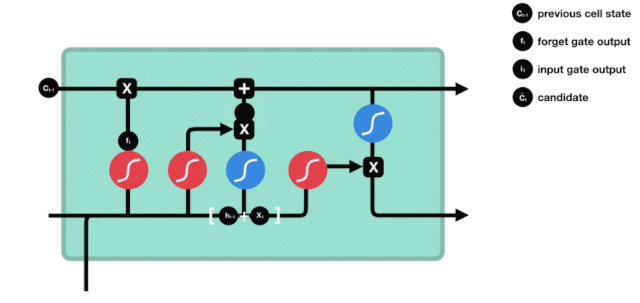
On peut voir que LSTM est en fait un petit modèle qui contient 3 fonctions d'activation sigmoïdes, 2 fonctions d'activation tanh, 3 multiples et 1 addition.

L'état des cellules

L'état cellulaire est au cœur du LSTM, il est la ligne noire en haut de la figure ci-dessus, et en dessous de cette ligne noire, il y a des portes, que nous présenterons plus loin. L'état cellulaire est mis à jour en fonction des résultats de chaque porte.

Les réseaux LSTM peuvent supprimer ou ajouter des informations sur l'état de la cellule par une structure appelée porte. La porte peut décider de manière sélective quelles informations passeront. La structure de la porte est une combinaison d'une couche sigmoïde et d'une opération de multiplication de points.

La porte oubliée

La première étape du LSTM est de déterminer quelles informations l'état cellulaire doit rejeter. Cette partie de l'opération est traitée par une unité sigmoïde appelée porte d'oubli.

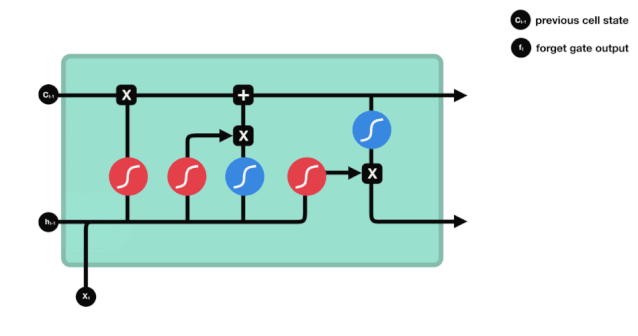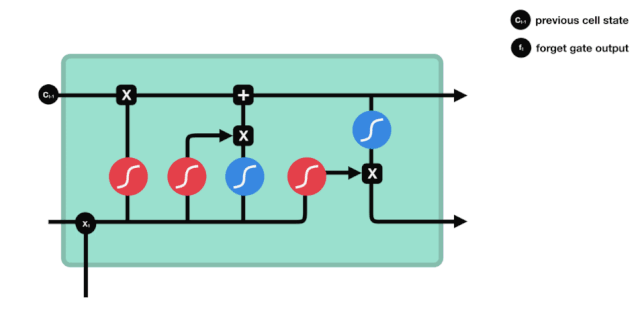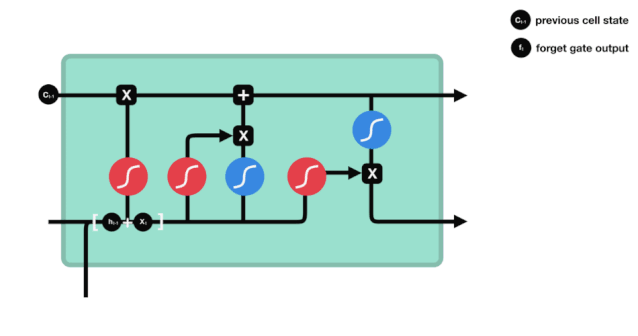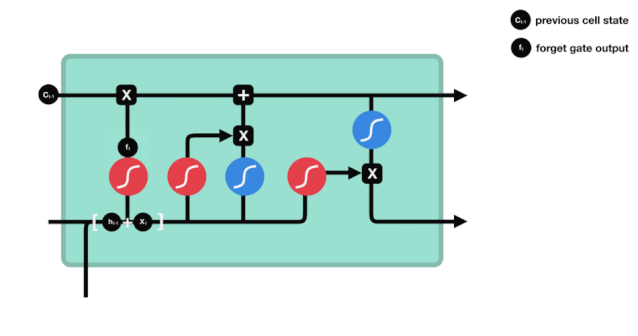
On peut voir que le verbe oublier produit un vecteur entre 0 et 1 en regardant les messages $h_{l-1}$ et $x_{t}$, dont la valeur 0 à 1 indique combien d'informations sont conservées ou rejetées dans l'état cellulaire $C_{t-1}$. 0 indique non conservé, 1 indique conservé.

L'expression mathématique est $f_{t}=\sigma\left ((W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

La porte d'entrée

L'étape suivante consiste à décider quelles nouvelles informations ajouter à l'état de la cellule, cette étape est effectuée en ouvrant la porte d'entrée.

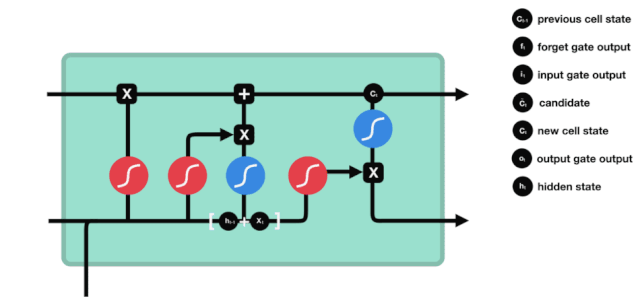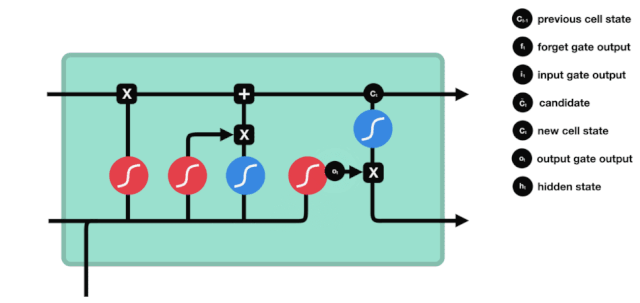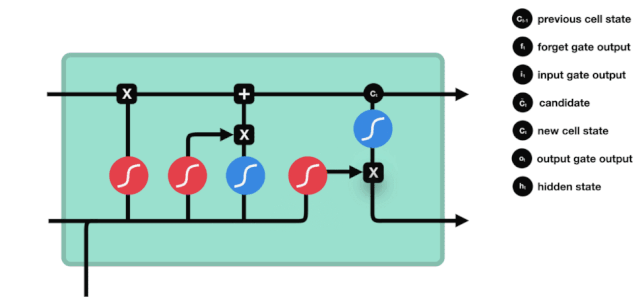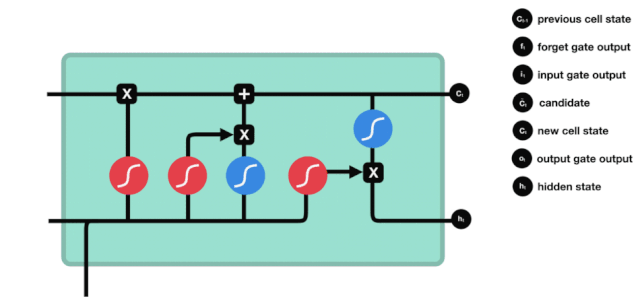
Nous voyons que les informations $h_{l-1}$ et $x_{t}$ sont à nouveau placées dans une porte d'oubli (sigmoïde) et dans une porte d'entrée (tanh). Puisque la porte d'oubli a une valeur de 0 à 1, donc si la porte d'oubli a une valeur de 0, le résultat $C_{i}$ après l'entrée ne sera pas ajouté à l'état actuel de la cellule, et si c'est 1, tout sera ajouté à l'état de la cellule, donc le rôle de la porte d'oubli ici est d'ajouter sélectivement le résultat de la porte d'oubli à l'état de la cellule.

La formule mathématique est: $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t}$

Porte de sortie

Après avoir mis à jour l'état de la cellule, il est nécessaire de déterminer quelles caractéristiques d'état de la cellule sont à l'entrée pour déterminer les caractéristiques d'état de la cellule à l'extérieur en fonction de la somme des entrées $h_{l-1}$ et $x_{t}$. Ici, l'entrée passe par une couche de sigmoïde appelée porte de sortie pour obtenir les conditions de jugement, puis l'état de la cellule passe par la couche tanh pour obtenir un vecteur d'une valeur comprise entre -1 et 1, qui est multiplié par les conditions de jugement obtenues par la porte de sortie pour obtenir l'entrée de l'unité RNN finale, comme illustré ci-dessous.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

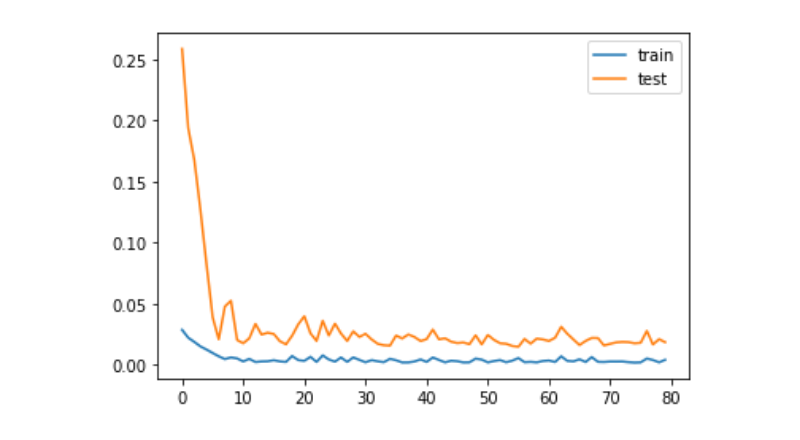
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Prévisions

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

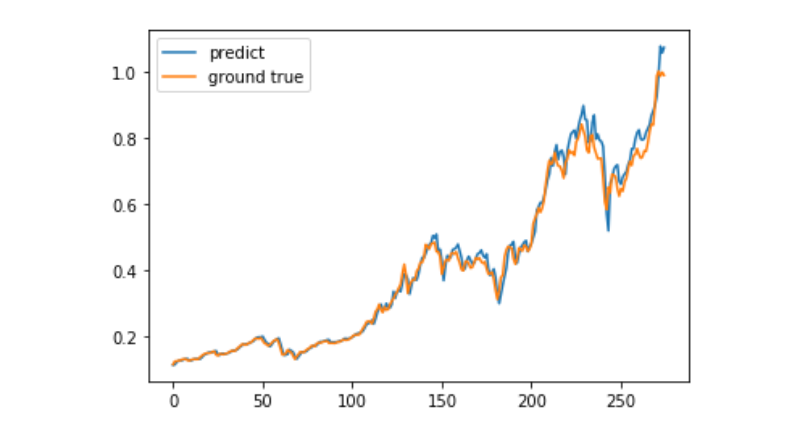
Il est très difficile de prédire l'évolution des prix à long terme de Bitcoin à l'aide de l'apprentissage automatique, et cet article ne peut être utilisé que comme exemple d'apprentissage. Le cas sera ensuite mis en ligne avec une image de démonstration dans le nuage de matrices, que les utilisateurs intéressés pourront expérimenter directement.