L'histoire de « l'évasion » et de la « survie » dans le jeu et l'investissement
 1
1
 2876
2876
L’histoire de « l’évasion » et de la « survie » dans le jeu et l’investissement
** Quand on parle de jeu et d’investissement, les gens sont généralement impatients d’apprendre les astuces pour gagner de l’argent. En fait, je pense que gagner de l’argent n’est pas facile à apprendre, il faut de l’expérience et de la perspicacité. Les débutants qui veulent améliorer rapidement leur niveau devraient d’abord s’entraîner à la défense. Pour commencer à écrire une série de romans d’évasion scolaire, il ne s’agit pas d’enseigner aux enfants à être absents de l’école, mais de discuter avec des amis et des collègues de la science des romans d’évasion scolaire. Inspiré par une interview que j’ai eue il y a trois ans avec le magazine de la semaine rouge de la bourse de Xi’an. Sous l’impulsion des journalistes, j’ai exposé mon point de vue sur les opérations de placement, j’ai publié un article sur la situation financière de l’économie mondiale et j’ai parlé de certaines transactions.
- ### Le secret de l’évasion de la mère de Fang Yang, l’un des plus grands manipulateurs de Wall Street
Je suis un peu déprimée.
L’interview ne parlait que de l’importance du contrôle des risques et donnait quelques exemples de réussite exceptionnelle de ses propres transactions. Comment est-ce qu’il est devenu un fugitif ? Cependant, en y réfléchissant bien, il a dû admirer l’acuité de l’éditeur du journaliste.
Le professeur Wu Qiang a pu commencer par un mystère du seigneur Yang et créer un mystère d’apprentissage de l’esclavage à la manière de Holmes. Il a dit qu’il pourrait aussi commencer par un mystère d’évasion et développer un mystère d’évasion de l’esclavage.
Je vous salue d’abord: je suis un peu perdu, mais si vous êtes loin, je vous pardonne.
Récemment, j’ai découvert que la partie qui intéressait le plus les lecteurs à propos de la vie de Wall Street était la partie de l’introduction sur le jeu ((auparavant, les commerçants de Londres avaient envoyé une version électronique à leurs amis qui avaient laissé leur boîte aux lettres, dans l’espoir d’aider tout le monde). Il semble que le 21 est plus proche de la foule que la baisse des taux d’intérêt.
Le plus important est de rester en vie.
Quand on parle de jeu et d’investissement, les gens sont généralement impatients d’apprendre les astuces pour gagner de l’argent, en fait, je pense personnellement que la méthode pour gagner de l’argent n’est pas facile à apprendre et nécessite beaucoup d’expérience et de perspicacité.
En résumé, il ne faut absolument pas se sacrifier avant la victoire de la révolution. Ne pensez pas que ce soit facile à faire, sans parler de ceux qui, autour de nous, ont essayé de s’enrichir avant de mourir, même parmi les meilleurs de la communauté des investisseurs, il y a beaucoup de gens qui sont tombés du ciel.
Voici quelques exemples:
Jesse Livermore: le héros du livre de mémoire de l’auteur de la Bourse de Pompéi, le génie du spéculateur, qui a commencé à zéro et a atteint 100 millions de dollars en 1929, a finalement fait faillite et s’est suicidé quelques années plus tard.
John Merryweather: ancien super-trader de l’investisseur de crypto-monnaie Salomon Brothers, qui a créé le fonds de couverture à long terme LTCM, qui avait un énorme capital de 4 milliards de dollars, mais qui a été presque détruit lors de la crise des obligations russes en 1998.
En 1988, il a fondé la société de titres de la Chine, connue comme le père des titres chinois, mais en 1995, il a perdu sa place dans l’affaire de la dette publique de 3,27 et s’est retrouvé pris au piège.
Tang Wanxin: Le groupe de sociétés qui dirigeait le groupe de sociétés de la famille Dron, qui avait un regard arrogant sur le marché des capitaux chinois, a fini par s’effondrer à la suite de la rupture de la chaîne de capitaux, entraînant l’effondrement de l’empire Dron.
Ces gens sont des génies du marché des capitaux, mais ils ont tous échoué. Leur expérience nous apprend qu’en ne prenant pas soin de contrôler les risques, il arrive ce qui est arrivé au pêcheur et au poisson rouge: ils ont lutté pour devenir pape et ils sont retournés dans leur cabane au bord de la mer.
Le plus important est de rester en vie.
Je ne sais pas, je ne peux pas.
Il y a de nombreuses années, j’avais l’habitude de voyager de Chinatown, à New York, à Atlantic City en bus pour gagner de l’argent, avec des gens qui travaillaient dans les couloirs des restaurants. La plupart d’entre eux essayaient de changer leur destin dans les casinos, mais ils étaient souvent payés très peu.
En revenant, j’ai gagné 800 dollars, elle en a perdu 4000. J’ai été soudainement ravie, 4000 dollars devrait être son revenu de plus d’un mois! En regardant les voitures pleines de compatriotes simples, je me suis soudainement sentie triste, et je haïssais ceux qui faisaient des affaires de grosse fortune, c’était comme envoyer des moutons dans la gueule du tigre! J’ai essayé de dire à la fille que jouer au bingo pendant longtemps était une perte, mais elle n’a pas voulu le croire, elle a dit que cette perte n’était que de la malchance et qu’elle devait revoir le livre la semaine prochaine.
J’ai perdu la parole, trop de gens qui ont échoué utilisent la chance comme prétexte.
Une victoire perdue est vraiment de la chance, 100 000 victoires perdues sont une théorie mathématique (le plus fort gagne presque toujours). Dans les jeux de casino où les joueurs jouent avec la probabilité de gagner, est-ce que la perte n’est qu’une question de temps ?
Il en va de même pour l’investissement.
Le marché boursier est un peu mieux que le casino, il devrait être un jeu de rendement positif à long terme. Mais en raison de facteurs tels que le jeu, les transactions secrètes et la taxe d’impression, il est difficile pour l’investisseur ordinaire de gagner le marché si le pari est trop fréquent, et il est même possible que le joueur perdra. Donc, ne croyez pas les soi-disant secrets secrets de ceux qui enseignent le marché pour devenir riche rapidement, 99% sont flou, 99% sont négligés.
Il y a un épée de l’époque de l’Empire Edo qui a combattu plus de soixante fois et n’a jamais été vaincu. En plus de son habileté, il a un secret: ne jamais jouer avec quelqu’un de plus fort que lui.
Je ne sais pas, je ne peux pas le faire.
C’est la première chose que les pirates et les investisseurs doivent garder à l’esprit.

Quels sont les avantages des casinos ?
Les casinos ne craignent pas que vous gagniez, ils craignent que vous ne veniez pas, parce que les jeux de casino sont essentiellement des jeux de hasard. Beaucoup de joueurs croient en la chance, et ceux qui gèrent les casinos croient en la probabilité, qui est la différence entre les perdants et les gagnants.
Par exemple, dans le cas de la roulette (voir la figure ci-dessous), le joueur peut parier sur n’importe quel nombre, et si la petite boule sur le rouleau s’arrête sur ce nombre, le casino perd 35 fois.
Ça sonne tentant, non ?
Le jeune homme qui s’est échappé de l’Europe dans le film Casablanca a été placé en détention pendant 22 jours, et il a payé son voyage aux États-Unis.
Nous allons faire une analyse simple.
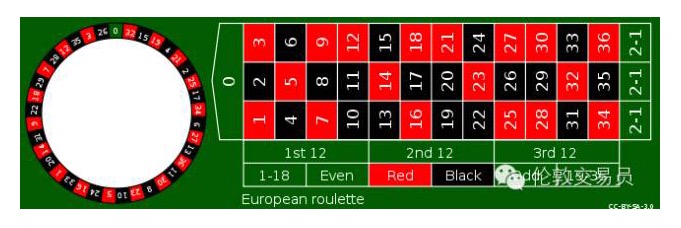
Si seulement 1 à 36 de ces 36 numéros, alors le joueur par pari 1 \(, en moyenne par 36 gagne une fois, 35 \) gagnés juste de contrebalancer les 35 autres perdent de l’argent. Mais le casino a ajouté un jeton 0 sur la gauche de la roue, le joueur de la victoire est devenu 1⁄37, 35 \( gagnés ne suffit pas pour contrebalancer les 36 autres perdent de l'argent, le casino occupe 1/37 = 2,70% de la probabilité de l'avantage, c'est-à-dire que le joueur par pari de 100 \), perd en moyenne 2,7 $.
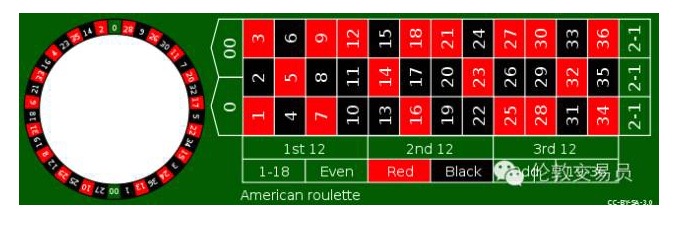
En plus de miser sur des numéros simples, les roulettes ont d’autres jeux tels que le rouge et le noir. Que ce soit un numéro unique de 1 contre 35 ou un noir rouge de 1 contre 1, le gain du casino est le même. Mais il y a une différence importante entre les deux: la fluctuation des gains et des pertes de miser sur un seul numéro est clairement plus grande que la mise sur le rouge et le noir.
Pour commencer, je voudrais simplement dire que la volatilité et la marge bénéficiaire sont les deux choses les plus importantes dans le jeu et l’investissement.
Il est préférable de ne pas toucher au jeu de hasard, car il y a une grande volatilité entre les gains et les pertes; les investissements dans le jeu de hasard doivent être peu volatils. Ce principe sera discuté plus en détail plus loin.
Pour en revenir au jeu de hasard, la plupart des jeux de casino sont conçus comme des jeux de roulette: le casino a un avantage de probabilité. Dans ces jeux, les joueurs peuvent gagner de l’argent en jouant à la chance et au hasard si seulement ils jouent quelques mains.
Mais les machines de casino ont été épuisées, et les mathématiciens ont trouvé une faille.
Une vieille histoire à 21 heures
Au début des années 1960, un mathématicien américain du nom d’Edward Thorp utilisa un ordinateur récemment apparu pour trouver des opportunités dans le jeu de 21 points et développa une méthode pour battre le casino par le comptage des cartes. Le professeur Thorp a mis en pratique la théorie et a remporté de grandes victoires au casino avec sa propre méthode de comptage des cartes.
Le best-seller de Thorpe, Beat the Dealer, qui s’est vendu à 700 000 exemplaires et a été classé par le New York Times comme le livre le plus vendu, a été largement dépassé par les revenus de la taxe sur les jeux d’argent. Cela montre une fois de plus qu’il est plus facile de vendre des canards que d’extraire de l’or.
Le principe du comptage des cartes de Thorpe n’est pas compliqué. Par exemple, la règle des 21 points: le joueur et le croupier (casino) s’affrontent pour voir qui est plus proche (mais pas plus) de la somme des points de la main.
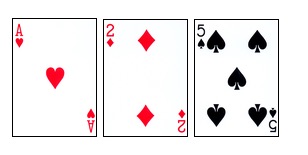
Le jeu de cartes commence lorsque le joueur et le croupier distribuent deux cartes, la carte du croupier étant clairement visible (comme le montre la figure ci-dessous). Le joueur décide alors de faire des actions spéciales telles que le craps, le doublage ou le stop à tout moment. Si le joueur dépasse 21 points (c’est-à-dire le “ craps “), il perd directement. Sinon, le stop est suivi d’une action du croupier.
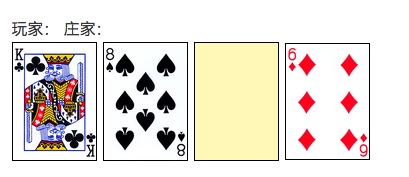
En outre, il existe une règle spéciale: une carte A et une carte de dix points ((10, J, Q, K) sont appelées Black Jack ((Blackjack), et le joueur qui les obtient gagne directement. Si le joueur obtient un Black Jack, il peut gagner 1,5 fois plus de jetons.
Il est évident que le joueur et le croupier ont tous deux un avantage dans un jeu de 21 points. L’avantage du croupier est de déclencher le jeu de hasard après le tirage: le joueur peut gagner sans combattre si le joueur est le premier à faire face.
Le plus grand nombre de cartes de dix points et de A, plus les chances de blackjack sont grandes, plus il est facile de casser les cartes, et l’avantage de la maniabilité du joueur est plus précieux. À l’inverse, plus il y a de petites cartes telles que 3, 4, 5, 6 et ainsi de suite, moins il y a de chances de casser les cartes, ce qui est plus avantageux pour le croupier.
Le 21 de l’ère Thorpe utilisait plus d’une ou deux paires de cartes de poker, et lorsque les cartes étaient nettoyées, le casino avait un avantage de probabilité d’environ 0,5%. L’ironie est que, à mesure que le jeu se déroulait, le rapport entre la grande carte et A devenait parfois élevé, ce qui rendait la probabilité favorable au joueur.
Un prêtre, Thorpe, a inventé le calcul des cartes, a écrit un best-seller, puis s’est rendu compte que Wall Street était riche, et plus tard, il s’est fait un nom dans le domaine des fonds de couverture.
En ce qui concerne le casino, il y a eu un groupe de compteurs de cartes qui ont maîtrisé le jeu de combat de So-Wei. Le casino a fait tout ce qu’il a pu pour repousser les compteurs de cartes, et les compteurs ont creusé des trous pour briser le blocus.
(Rassurez-vous, les histoires racontées finissent toujours par être retournées à l’investissement.
Le groupe de comptables du MIT
Parlant de Thorpe, le casino a eu d’autres ennuis avec le compteur de cartes. Au fil du temps, le casino a accumulé une liste noire. Si la personne sur la liste est reconnue à la table à 21 cartes, elle est généralement immédiatement expulsée du pays.
Dans les années 80, un détective engagé par le casino a rassemblé des listes noires et a trouvé un indice important: de nombreux joueurs de cartes vivaient près de Cambridge, dans le Massachusetts. Vous n’en avez peut-être pas entendu parler, mais vous n’en avez probablement pas entendu parler des deux universités qui se trouvent dans cette ville: Harvard et MIT.
La vérité a été révélée par un groupe de joueurs de cartes composé principalement d’étudiants du MIT !
Il s’agit d’une organisation qui fonctionne sous un masque commercial: quelqu’un crée le capital, quelqu’un gère la gestion, quelqu’un joue les cartes, l’ensemble du capital d’investissement du groupe et le mode de contrôle du risque du groupe est un modèle de fonds de couverture. Le plus grand avantage du gangsterisme est qu’il peut éviter les risques auxquels sont confrontés les hackers individuels: la volatilité des gains et des pertes est très élevée, quelle que soit votre technologie, la malchance à court terme peut également entraîner la perte de capital, et les opérations de groupe peuvent dissiper ce risque.
Michael, par exemple, qui comptait les cartes, lançait des pièces de monnaie prédéterminées à chaque petit pari, quand la situation était favorable, et James, qui se faisait passer pour le petit frère, venait et plaçait un pari de 1000 dollars.
Le groupe du MIT a été en activité pendant plus d’une décennie, avec des participants de l’université de Harvard et du MIT, dont des Chinois ayant remporté une médaille d’or aux Jeux olympiques. Les soldats qui font de l’eau dans les camps de fer ont toujours été des génies en mathématiques. Le groupe aurait gagné des millions de dollars, et plus tard, un auteur a écrit un livre sur les exploits du groupe du MIT.
Au milieu des années 90, l’économie américaine était en plein essor, les membres des gangs se déplaçaient vers Silicon Valley, Wall Street, etc., et les gangs du MIT se sont dispersés. Cela semble également prouver une vérité: les jeunes ont des emplois et le taux de criminalité diminue.
Quelques années plus tard, un de mes camarades de classe, un pêcheur chinois, a rencontré par hasard le jeu de cartes à 21 points. J’étais très intéressé. À l’époque, je n’avais jamais entendu parler de Soup et je ne savais pas que le livre de So Zhong était vendu pour une dizaine de dollars, j’ai acheté le soi-disant livre de secrets de cuisine à 100 dollars d’un grand joueur nommé Kadosa.
Mais le lac n’est plus le même de l’année dernière.
La confusion au sujet du pari
Après avoir appris à compter les cartes, j’ai été très enthousiaste à l’idée de me rendre à Las Vegas pour un petit tour de force. Le résultat a été très bon, j’ai gagné une grosse somme de 100 dollars, ce qui est une véritable mine d’or !
J’ai commencé à m’apercevoir que le gravier en aluminium d’Atlantic City n’était pas très bon, que j’avais généralement peu de chances de gagner, et que les gains et les pertes étaient très volatils.
Comme nous l’avons dit plus haut, le compteur de cartes se base sur la proportion de cartes grandes et petites dans le reste de la carte, et le plus gros pari est fait lorsque la proportion de cartes grandes est supérieure à la normale.
Il est évident que le ratio augmente le plus facilement dans les deux cas, le premier lorsque les cartes restantes sont rares, et le second lorsque le jeu de 21 points n’utilise que 1 à 2 cartes de rechange. Le jeu de 21 points de l’ère Thorpe a précisément ces deux caractéristiques: seulement 1 à 2 cartes de rechange, et le donneur (le dealer) va presque laver les cartes à la lumière, donc le ratio des grandes cartes augmente souvent, et les joueurs ont beaucoup d’occasions de parier quand la situation est favorable.
Le casino a naturellement aussi des stratagèmes de haut niveau, comprenant que la meilleure défense douce contre le comptage des cartes est de tenter de contrôler la fluctuation du rapport entre les cartes grandes et petites, de sorte que le casino a fait deux mesures de poison. La première est l’augmentation de 21 points de cartes, de 1 à 2 paires généralement modifiées à 6 à 8 paires.
Il est évident qu’avec une carte en plus, le ratio des cartes plus grandes et plus petites ne change pas facilement.
Le second est de laver les cartes à l’avance, pour éviter les proportions les plus susceptibles de fluctuer. Les casinos de Las Vegas sont nombreux et très compétitifs, les casinos réservent des jeux de 21 points de 1 à 2 cartes secondaires pour les joueurs, et je gagne principalement dans ces jeux.
Il s’avère que mon lac n’est plus le lac de l’époque de Thorpe.
Cependant, la loi de la majorité dit seulement que la révolution du cuivre finira par gagner le cuivre, mais elle ne garantit pas que vous ne sacrifierez pas le cuivre avant la victoire de la révolution du cuivre. La dynamique de la perte de 21 points est si grande que si vous rattrapez un cygne noir (Black Swan, petit événement de probabilité), n’avez-vous pas de la gloire ?
Si je ne gagne que 10 000 dollars, ce n’est pas facile d’attendre que nous ayons un avantage de probabilité de 1% sur le casino.
Il y a des gens qui ne sont pas d’accord avec ce que je dis.
J’ai misé 20 dollars, et j’ai gagné 2 cents en moyenne.
J’ai perdu la lumière en rattrapant une cigogne moins noire (j’ai perdu 5 fois de suite). Il semble que 20 dollars soit trop peu, 2000 dollars trop, et que la meilleure mise devrait être entre les deux.
Une personne de haut rang a déjà donné la réponse.
(C’est un peu la théorie de l’investissement que nous allons voir…)
Formule de Kelly
Comme je l’ai dit plus haut, il faut de la compétence pour parier quand la situation est favorable. Il y a trop peu de chances de perdre et trop de risques de perdre. Quels sont les paris appropriés?
f* = (bp - q) / b où f* = le pourcentage de capital investi sur le total. p = probabilité de gagner q est la probabilité d’échec, q est 1-p. b = probabilité, par exemple en pariant sur un seul chiffre dans le tour de roulette, b = 35, parier sur le rouge et le noir, b = 1。
Dans le cas des 21 questions de pari mentionnées précédemment, en supposant que le pari total soit de 10 000 dollars et que la probabilité de gagner soit de 51% avec une cote de 1:1 (les chances réelles de gagner et de perdre sont légèrement différenciées, mais la distance n’est pas grande), le meilleur pari donné par la formule de Kelly est:
\(10000 * (1 * 0.51 - 0.49)/ 1 = \)200 Je sais que beaucoup de gens sont déçus par les formules mathématiques, mais pour jouer aux jeux d’argent et d’investissement, il faut absolument apprendre les mathématiques. L’important n’est pas de calculer les chiffres avec des formules, mais de comprendre le sens réel des formules.
Tout d’abord, la bp - q de la molécule dans la formule représente la probabilité de gagner un pari, appelée en mathématiques l’expectation, la formule de Kelly indique que le pari est placé sur le jeu avec une valeur attendue positive, ce qui est la vérité la plus fondamentale de tous les jeux de hasard et d’investissement, c’est-à-dire que le pari précédent n’a pas de certitude et ne pariera jamais.
Deuxièmement, la partie gagnante doit être divisée par la partie gagnante. Autrement dit, dans le même cas, les chances sont plus faibles, plus vous pouvez parier.
Jeux de hasard: 20% de chances de gagner, 1 de chances de gagner, 5 de chances de perdre.*20% - 80% = 20% La probabilité de gagner est de 60%, 1 contre 1. bp - q = 1*60% - 40% = 20% Jeux de hasard: 80% de chances de gagner, 1 de défaite, 0,5 ◦ bp - q = 0,5*80% - 20% = 20%
Les trois jeux ont la même valeur d’attente mathématique, soit 20%, c’est-à-dire que le pari de 100 dollars gagne en moyenne 20 dollars. Selon la persévérance de la plupart des gens du pays, je crains de choisir le jeu de la petite loterie, n’est-ce pas?
En réalité, la plupart des joueurs de casino sont des pirates.
Qui aime jouer aux jeux de hasard ?
Les investisseurs professionnels de Wall Street jouent aussi beaucoup aux jeux de hasard, parce qu’ils utilisent le levier (le pari). Nous en parlerons plus tard.
Enfin, la formule de Kelly souligne l’importance cruciale de la maîtrise des risques: même dans des jeux à valeur attendue positive, il est impossible de miser trop. Mathématiquement parlant, le pourcentage de fonds mis en jeu dépasse la valeur de Kelly, tandis que la vitesse de gain à long terme diminue et augmente considérablement la probabilité de pertes catastrophiques.
Pourquoi le monde de l’investissement a-t-il perdu sa fortune au profit de quelques grands techniciens locaux ? La plupart du temps parce qu’ils ont misé trop d’argent.
Le Liverpool bat le Maitland
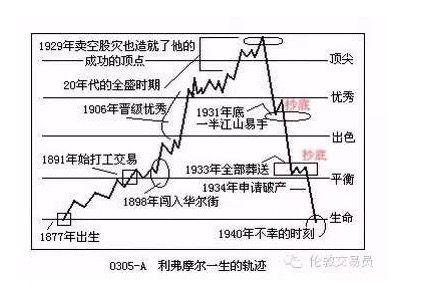
Le 28 novembre 1940, 16 ans après la publication de la formule Kelly, un ancien solitaire de la rue de Wall Street sort son pistolet du placard du Waldorf à New York, et laisse un mot à sa femme: “Oh… j’en ai marre de me battre… c’est la seule délivrance.
Jesse Livermore, l’immortel héros du livre de souvenirs de l’auteur de la bourse de la licorne, s’est éteint ainsi tristement dans la légende.
Si vous n’avez pas encore lu Reminiscences of a Stock Operator, je vous recommande vivement de le faire. De nombreux gestionnaires de fonds spéculatifs de classe mondiale ont fait l’éloge de ce livre.
Il s’est retrouvé dans une période primitive et a résumé les règles que beaucoup d’investisseurs modernes considèrent comme des classiques: gagner plus quand on gagne, perdre moins quand on perd, ne pas sous-estimer les opinions des autres ou les soi-disant secrets de l’initié, et un ensemble complet de techniques d’investissement.
Plus impressionnant encore, Livermore n’était pas seulement un théoricien, il était aussi un praticien. Sa vie d’affaires a évolué de quelques millions de dollars en 1907 à une valeur de 100 millions de dollars en 1929! À l’époque, les voitures ne se vendaient que pour quelques centaines de dollars, et Livermore a gagné 100 millions de dollars en faisant des affaires, ce qui équivaut à plus de 10 milliards de dollars aujourd’hui!
Ce n’est pas un fait documenté, mais si l’on analyse de près ses habitudes de négociation, il n’est pas difficile de trouver des indices.
La carrière de Livemore a débuté avec Bucket Shop.
À la fin du XIXe siècle, les marchés boursiers américains étaient très actifs et les progrès technologiques ont permis à des gens ordinaires de loin de New York de jouer en temps réel à la spéculation boursière: des machines à cité automatiques connectées à des lignes de télégraphe pouvaient diffuser à tout moment les dernières transactions de la Bourse de New York dans tout le pays. À l’époque, de nombreuses personnes voulaient participer à la spéculation, mais le manque de fonds pour acheter et vendre des actions a permis aux marchands de l’occasion d’attirer ces personnes vers les casinos de paris boursiers.
Il y a des machines à sous dans les casinos où les joueurs semblent négocier des actions qui sont en fait de la taille d’une pièce de monnaie. Par exemple, si la dernière offre d’une action est de 80 dollars, le joueur peut acheter une pièce de monnaie de 1 dollar, et si la machine à sous affiche un prix de 79 dollars ou moins, vous êtes désolé de vous perdre; si la machine à sous affiche 81 dollars, le joueur peut gagner 1 dollar de profit, et ainsi de suite.
Comment les voyous des casinos boursiers gagnent-ils de l’argent ?
En plus d’exploiter la tendance des masses à parier souvent à tort, ils ont conspiré pour manipuler le marché avec certains courtiers. Par exemple, à 80 dollars, de nombreux joueurs ont parié le gros lot, le croupier de casino a fait pression sur le prix de l’action par un collègue de la Bourse de New York, et le casino a mangé le gros pari si un prix de 79 dollars a été inscrit sur le machine à sous automatique.
A l’époque, alors qu’il n’avait pas beaucoup d’argent, Livermore s’est mis à jouer au casino et a appris à lire la bande pour prédire le prix du marché en fonction des offres. Il n’y avait pas d’ordinateur à l’époque, pas de diagramme K en temps réel, et le Kung Fu de Livermore était le prototype de l’analyse technique.
Mais je doute qu’il ait aussi développé un mauvais vice dans les casinos boursiers: le pari est trop élevé.
D’après l’analyse de la formule de Kelly, la garantie ultra-basse des casinos boursiers est en fait le tueur à gages des joueurs. Le levier est si grand que la perte de la valeur est bien supérieure à celle de Kelly.
Il a eu la chance d’être aidé par des nobles et de saisir plusieurs occasions importantes pour atteindre le sommet en 1907, 1915 et 1929.
J’imagine que c’est le problème des paris à grande échelle qui a fait perdre à Livermore tout son argent quelques années seulement après avoir atteint 100 millions de dollars.
Quels miracles ce génie pourrait-il accomplir s’il combinait sa méthode de gestion de fonds basée sur la formule de Kelly avec sa maîtrise du marché ?
Il n’y a pas de si dans l’histoire.
Liverpool est passé comme une étoile, peut-être des décennies plus tôt.
La théorie de la gestion de fonds et du contrôle des risques a commencé à se former dans les années 50.
La formule de Kelly indique que les jeux à gros gains et à faible volatilité permettent de parier plus gros. Alors, comment quantifier les gains à gros gains et à faible volatilité? Un célèbre indicateur a été proposé par un savant contemporain de Kelly.
Le ratio de Sharpe
Les avantages et les inconvénients de l’évaluation des opportunités d’investissement doivent être considérés de manière globale, à la fois en termes de revenus attendus et de risques. Comment quantifier cette idée? Dans les années 1950, quelqu’un a proposé d’utiliser le rapport entre les attentes de rendement et la volatilité comme indicateur de mesure des opportunités d’investissement.
S = (R r) / σ, où: R = le rendement attendu de l’investissement r = le rendement d’un investissement sans risque (qui peut être interprété comme le rendement d’un investissement dans des obligations d’État) σ = Divergence standard du taux de rendement (le plus souvent utilisé pour mesurer la volatilité)
Plus le Sharpe ratio est élevé, plus les opportunités d’investissement sont de meilleure qualité.
A. Investissement: Excédent (excédent de la dette publique) de rendement attendu à 10%, écart standard de 20%, ratio de Sharpe à 0,5 Investissement B: Expectative de rendement supérieur à 5%, écart standard de 5%, ratio Sharp de 1
À première vue, l’investissement A avec des attentes de rendement élevées peut sembler être une opportunité plus avantageuse. En fait, l’investissement B est plus avantageux, car son taux de Sharpe est élevé, ce qui signifie que l’investisseur peut échanger 1 unité d’acier pour 1 unité d’acier pour plus d’attentes de rendement. La même conclusion peut être tirée du point de vue de l’investissement à effet de levier: en supposant qu’un investisseur finance un prêt à un taux d’intérêt r, en doublant 1 levier sur une opportunité d’investissement B, un investissement B à effet de levier devient une attente de rendement de 10%, un écart de 10% standard, la même attente de rendement que l’investissement A, mais moins de risques.
Quel est le Sharpe ratio pour être un bon joueur de poker ?
Prenons un exemple concret: le rendement moyen annuel à long terme des actions américaines est d’environ 10%, la volatilité est d’environ 16%, le taux d’intérêt sans risque est d’environ 3,5%, donc le ratio Sharpe est d’environ 0,4.
Pour les investisseurs de longue durée, le rapport risque/rendement des actions américaines est passé de mode. Pour les gestionnaires de fonds de couverture, le ratio Sharpe est trop bas: en supposant que votre objectif soit un rendement annuel de 20%, il est nécessaire d’utiliser 2,5 fois plus de levier (rendement attendu = 2,5).*10% - 1.53,5% ≈ 20%), cela signifie que le rendement moyen sera inférieur à 2,5 pour une année sur six.(10% - 16%)- 1.5*Si vous perdez plus de 20%, le client risque de perdre.
Généralement, un ratio de Sharpe supérieur à 1 est un bon pari. Cette opportunité n’est pas fréquente dans les jeux de placement simples, de sorte que les investisseurs professionnels utilisent souvent des méthodes de couverture pour modifier le jeu de placement et améliorer le ratio de Sharpe.
Par exemple, si vous inventez une méthode de couverture mutuelle d’actifs pour obtenir un ratio Sharpe de 2, vous pouvez avoir le courage d’ajouter du levier (les étudiants qui savent mathématiques peuvent calculer eux-mêmes la probabilité de perdre de l’argent) et les investisseurs vont probablement investir dans votre fonds de couverture.
Mais les méthodes d’investissement couvertes par un effet de levier ont souvent un seuil d’échec: il faut emprunter beaucoup d’argent, les exigences de liquidité sont élevées, donc les crises soudaines sont souvent problématiques. L’exemple de LTCM et du fonds Global Alpha de Goldman Sachs a été analysé dans le Wall Street Journal.
Le ratio de Sharpe est également défectueux, car il suppose que le rendement est normal, alors que la distribution réelle du rendement des investissements a une queue de riz (la probabilité de perdre beaucoup d’argent est plus élevée que l’estimation de la distribution normale), donc il y a un problème de sélection des opportunités d’investissement simplement en fonction du ratio de Sharpe et il est également facile à manipuler. Ce sujet n’est pas discuté ici.
Pour les investisseurs ordinaires, le Sharpe ratio suggère de choisir des investissements plus rentables que moins rentables, en tenant compte du risque et du rendement. C’est exactement le point de vue évoqué dans l’article précédent: choisir un jeu à rendement positif avec une faible volatilité, choisir un jeu à rendement négatif avec une grande volatilité si nécessaire.
Le ratio de Sharpe parle de la façon de sélectionner les pièces de jeu, tandis que la formule de Kelly parle de la façon de choisir les mises après le jeu pour obtenir le meilleur taux de rendement à long terme.
Note complémentaire sur le Sharpe ratio
En ce qui concerne le Sharpe ratio, les questions se concentrent sur plusieurs aspects:
Première question: dans l’exemple de la Bourse américaine, comment calculer que le rendement moyen de l’or est inférieur à -6% sur une période de 6 ans ?
Le ratio de Sharpe suppose que le rendement d’un investissement correspond à une distribution normale (voir la figure ci-dessous). Mathématiquement parlant, la somme d’un grand nombre d’événements aléatoires indépendants correspond généralement à une distribution normale. Par exemple, le lancer continu d’une pièce de monnaie, face positive est de 1, face inverse est de 1, la somme des résultats après une grande répétition correspond à une distribution normale.
L’hypothèse d’une distribution normale, bien qu’imparfaite, constitue le cadre de base de la compréhension du problème. Le graphique ci-dessous montre les valeurs de probabilité d’une distribution normale. Par exemple, la probabilité de retour entre 0 et 0,5 fois l’écart type est de 19,1% (la partie verte du graphique).
De même, la probabilité d’un rendement inférieur à 1 fois l’écart standard (la partie orange du graphique) est d’environ 16%. Cela s’applique aux marchés boursiers américains (le rendement moyen est de 10%, l’écart standard est de 16%), et le rendement annuel est inférieur à 1 fois l’écart standard, soit de 10% à 16% = -6%. La probabilité d’un rendement inférieur à -6% est d’environ 1⁄6.
Deuxième question: est-ce que l’hypothèse du Sharpe ratio est en contradiction avec la réalité ?
Bien sûr que oui. L’hypothèse d’une distribution normale n’est pas parfaite. En fait, le mouvement des marchés boursiers n’est pas complètement indépendant de la courbe aléatoire, sinon nous n’aurions pas besoin de nous soucier d’étudier une loi. Par exemple, dans les crises financières, le mouvement des marchés boursiers a une très forte corrélation séquentielle, la soi-disant courbe de tendance de la courbe, ce qui entraîne le phénomène de retour des marchés boursiers réels avec une courbe de la courbe de la courbe, c’est-à-dire que la probabilité de courir à la position extrême de la courbe est supérieure à l’estimation de la distribution normale.
En outre, le taux de rendement sans risque de l’indice de Sharpe, r, est une notion vague, et le coût de financement des investisseurs n’est pas r. De plus, le calcul de la volatilité n’est pas une question simple.
La troisième question: à quoi sert le ratio Sharpe pour un investisseur ordinaire ?
La prochaine fois que quelqu’un vous dira que j’ai gagné en moyenne 30% au cours des trois dernières années, vous pourrez vous poser une question timide: quelle est la volatilité de l’or ?
Exemple d’analyse des résultats des fonds de couverture
Pour évaluer la performance d’un investissement, il ne suffit pas de regarder le taux de rendement, il faut aussi prendre en compte les facteurs de risque. Examinons maintenant un exemple concret d’un fonds de couverture. Le tableau suivant présente les taux de rendement annuels moyens de plusieurs grands fonds de couverture bien connus (source: HSBC Research Report).
Tableau 1
| - | - |
| - | Taux de rendement annuel composé |
| Fonds A | 14.15% |
| Fonds B | 15.17% |
| Fonds C | 15.20% |
| Fonds D | 79.17% |
| Fonds E | 2.78% |
Vous choisissez le fonds D, avec un taux de rendement annuel de 79%, n’est-ce pas ? Félicitations, vous avez choisi le Paulson Credit Opportunities Fund, qui a été créé et géré par Paulson (le même nom que l’ancien secrétaire américain au Trésor, mais sans lien de parenté) et qui est devenu l’un des gestionnaires de fonds les plus célèbres.
Mais nous venons d’en discuter: il ne suffit pas de regarder le taux de rendement, il faut aussi prendre en compte le risque. Le tableau 2 présente les valeurs de volatilité et de Sharpe ratio des différents fonds (en supposant un taux de rendement sans risque de 3%).
Tableau 2
| - | Taux de rendement annuel composé | Variabilité des taux de rendement | Le ratio de Sharpe |
|---|---|---|---|
| Fonds A | 14.15% | 5.94% | 1.9 |
| Fonds B | 15.17% | 12.30% | 1.0 |
| Fonds C | 15.20% | 4.53% | 2.7 |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 |
| Fonds E | 2.78% | 12.21% | <0 |
En d’autres termes, la volatilité du fonds C est seulement un dixième de celle du fonds Paulson, et si l’investisseur n’est disposé qu’à assumer un risque de volatilité fixe, il peut investir 1 dollar dans le fonds Paulson ou 10 dollars dans le fonds C, avec un risque similaire, mais un rendement plus élevé dans le fonds C !
Le fonds C est le Millennium Intl Ltd (fond millénaire), l’arbre toujours vert de l’industrie des fonds de couverture, dont les gestionnaires ont eu quelques hauts dirigeants d’origine chinoise. Du point de vue des investisseurs, il est un peu difficile de choisir entre le fonds Paulson qui a gagné ou le fonds millénaire qui a été solidement sélectionné.
Si l’on analyse plus en profondeur et si l’on compare seulement le ratio de Sharp, on a l’impression que le ratio de Paulson est un peu inéquitable: bien que son volatilité soit élevée, il s’agit principalement d’un taux de volatilité à la hausse, un taux de volatilité qui se produit dans le processus du profit, et non pas un risque. Les investisseurs ont peur de perdre de l’argent, en particulier des dizaines de pour cent de pertes immédiates.
Tableau 3
| - | Taux de rendement annuel composé | Variabilité des taux de rendement | Le ratio de Sharpe | Déclin le plus élevé (temps de l’événement) |
|---|---|---|---|---|
| Bluecrest | 14.15% | 5.94% | 1.9 | -4.83% (2003) |
| FORE (capital à l’avant) | 15.17% | 12.30% | 1.0 | -27.01%(2008) |
| Le millénaire | 15.20% | 4.53% | 2.7 | -7.24% (1998) |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 | -10.41%(2007) |
| Drake | 2.78% | 12.21% | <0 | -51.74%(2007-2009) |
Il est intéressant de noter que le fonds A (Bluecrest Capital) a connu sa plus forte baisse de moins de 5% en 2003, et que le fonds a évité des pertes importantes pendant la grande crise de 2007-2008, ce qui est assez attrayant. Bluecrest et Millennium appartiennent tous deux au type de fonds stables, évitant la crise des subprimes, et il semble difficile de les distinguer.
Les trois fonds sont donc favorisés par les investisseurs institutionnels, avec respectivement 8,6 milliards de dollars, 10 milliards de dollars et 6,3 milliards de dollars sous gestion. Il semble logique que les gens puissent faire des économies.
Le fonds E (Drake Absolute Return Fund) était aussi un grand fonds gérant des milliards de dollars, mais il a subi des pertes énormes de plus de 50% pendant la crise financière, ce qui a fait perdre la confiance des investisseurs et les a retirés, de sorte que le capital géré par Drake est maintenant de seulement 200 millions de dollars.
Enfin, le fonds B, avec un rendement annuel composé à long terme de 15%, un ratio Sharp 1, un bon indice composé, a surmonté la crise bien qu’il ait subi une perte de 27% en 2008. On peut dire que le fonds B est assez fort, donc il est également devenu un grand fonds gérant plusieurs milliards de dollars.
Dans cet exemple réel d’évaluation de la performance d’un investissement, nous pouvons voir l’utilité d’indicateurs de risque tels que le Sharpe ratio et le maximum de baisse. Les investisseurs débutants ont souvent le tort de ne voir que le rendement et pas le risque. La formule de Kelly est bonne et le Sharpe ratio est bon, et en fait nous dit une chose: trouver un équilibre entre le rendement et le risque.
Les marchés boursiers comportent des risques, il faut donc être prudent. Les informations fournies sont à titre indicatif et ne constituent pas une recommandation d’investissement !
Il a été publié par le blogueur SystoKin.