Stratégie de trading du joueur

Le thème de cet article est en fait une phrase de Jobs: “Nous faisons moins de hasard pour le rendre plus aléatoire”.

Les paragraphes qui suivent sont des préfaces, mais il est conseillé de les lire patiemment avant d’en lire le texte original, afin de mieux connaître le savoir-faire de l’assistant de Joe.

• ##### La phrase la plus citée dans la Déclaration d’Indépendance des États-Unis est: “Tous les hommes sont créés égaux”. Mais plutôt que d’être une déclaration de fait, cette phrase est plus proche de notre souhait que nous faisons en nous inclinant à la prière: nous voulons que tous les hommes soient égaux.

Le vœu suggère que cela n’existe pas: quelqu’un qui conduit une voiture depuis son enfance, quelqu’un qui a un QI de 180 et qui, à trois ans, calcule des calculs avec un crayon et écrit un corps mince.

L’inégalité dont nous allons parler aujourd’hui est encore plus déséquilibrée que celles-ci: pourquoi quelqu’un gagne toujours !

Il y en a toujours quelques-uns dans chaque entreprise, et chaque année, ils gagnent un prix au loto, disant que ce n’est pas une bonne chose d’être attaché par la fortune. J’ai acheté un café et j’en ai acheté un et j’en ai reçu un ouvert, et j’en ai acheté un et j’en ai reçu un, j’étais tellement excité que je ne pouvais pas dormir la nuit (bien sûr, cela pouvait aussi être dû à une consommation excessive de caféine).

C’est la seule expérience qui puisse être qualifiée de victoire consécutive.

Les prix consécutifs sont injustes, ils arrivent toujours à la mère d’un autre.

Supposons que la société compte 200 personnes et que la probabilité de remporter le premier prix du tirage au sort annuel est de ¹⁄₂₀₀ = 0,5%, la probabilité de remporter le premier prix deux années consécutives est de 0,5% x 0,5% = vingt-cinq sur un million, ce qui est assez faible.

Mais en fait, c’est la probabilité que quelqu’un (vous) gagne le premier prix 2 ans de suite. La probabilité que quelqu’un gagne le premier prix 2 ans de suite est de 200 x 0,5% x 0,5% = 0,5%, c’est la même probabilité que vous gagnez le premier prix 1 fois dans votre tirage au sort.

La probabilité qu’une personne gagne deux fois le prix en trois ans est: 1 - La probabilité que trois personnes différentes gagnent le prix en trois ans = 1-200 × 199 × 198 / 200 × 200 × 200 = 1,5%

En d’autres termes, si vous pensez que ce n’est pas une bonne idée de me donner un prix en 3 ans, alors il est tout à fait raisonnable de mordre le mouchoir de quelqu’un d’autre en 3 ans et de gagner 2 prix en 3 ans.

Tu peux fumer toute l’année.

Et il est encore plus choquant que le gars qui a remporté deux prix consécutifs dans la même année et qui se considère comme le gagnant du prix de la chanson d’or du jour de mai ?

Pour revenir à l’exemple de l’entreprise de 200 employés, supposons qu’il y ait 10 prix et que les employés puissent en remporter plusieurs. La probabilité que 10 prix aient été remportés par 10 personnes différentes = 1-200 × … × 191 / … 200 × … × 200 = 20,4%

Il y a 1 chance sur 5 qu’un de vos collègues vous dise que vous avez gagné le concours et que moi j’ai gagné le concours… c’est un peu amer.

Les traders londoniens: le moment est venu

Ce n’est pas du hasard.

Ce genre d’erreur peut sembler peu probable, mais en fait, le phénomène de la vie est tellement ridicule que, comme la lecture aléatoire de chansons, si vous ne supprimez pas les chansons que vous avez écoutées de la liste de lecture, une liste de lecture de 10 chansons, en essayant de ne pas répéter une seule chanson dans un ordre aléatoire, ne peut que 10 !/1010 = 0,036%, soit une probabilité inférieure à celle d’une tâche impossible, soit une probabilité inférieure à celle de Tom Cruise qui n’a pas divorcé. Le problème peut être résolu en supprimant directement les chansons que vous avez écoutées de la liste de lecture, mais l’inconvénient est qu’il faut au moins une chanson après 10 pour entendre la deuxième.

On dit que le programme de lecture aléatoire d’Apple consiste à jouer différents chanteurs, différents airs, afin de donner à l’utilisateur l’impression qu’il n’y a aucun lien entre chaque chanson. Jobs a dit: “Nous réduisons le hasard pour donner un peu plus de hasard”.

• #### Bon, les préparatifs sont faits, maintenant on peut commencer à écrire.

Le modèle du joueur par rapport à la transaction (voir le dernier film de Mark Wahlberg, The Gambler, mais les traders londoniens disent que le film n’a pas été bien vu)

Quand on négocie, à n’importe quel moment, on devine une direction, si on fait une erreur, on double à l’envers, on ouvre une position et on revient, le prix revient toujours, il est impossible de monter sans revenir en arrière ((pas tomber sans revenir en arrière)), chaque fois que je double, je reviens, je reviens une fois de plus et je gagne de l’argent.

La prochaine fois que vous gagnez, vous gagnez 4 yuans, 1 yuans de plus, et si vous vous trompez, vous gagnez 4 yuans, 8 yuans de plus, donc 1 + 2 + 4 = 7, ou 1 yuans de plus.

Si vous ne savez pas ce que vous gagnez, vous gagnez 1 yuan par transaction.

Et puis encore, encore, encore, je gagne toujours de l’argent !

Cette illusion classique des joueurs, comme les escroqueries pontificales, est d’une vitalité stupéfiante, dure longtemps, ne s’effondre pas, et trompe les spéculateurs de génération en génération.

La probabilité ou la valeur attendue d’un jet de pièce est de 0,5, mais si elle est lancée une seule fois, la probabilité d’un jet de pièce est de 0 ou 1 (distant de 0,5). Avec l’augmentation du nombre de lancements (c’est-à-dire l’augmentation du nombre d’échantillons), la probabilité d’un jet de pièce est de 0,5. Cependant, selon la loi de la petite quantité d’échantillons de la psychologie cognitive, l’influence de la taille de l’échantillon est généralement ignorée, car les petits échantillons et les grands échantillons ont la même valeur attendue.

Il y a eu beaucoup de positifs, mais il y a toujours eu une forte probabilité de négatifs.

Sur les tables de roulette, il y a toujours un grand nombre de joueurs qui choisissent de miser sur le noir après plusieurs apparitions consécutives de rouge.

En utilisant cette stratégie, la courbe de financement devrait être la suivante:

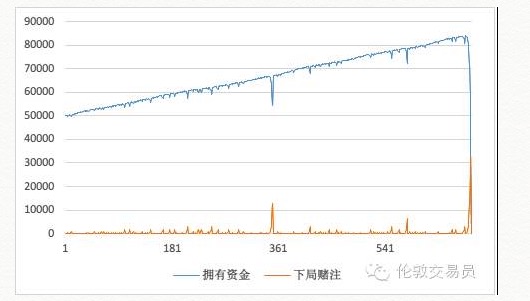
Dans la pratique, la courbe des capitaux s’est orientée vers le haut et semble avoir été stable. En pratiquant 361 fois, nous voyons une série d’erreurs, et si nous persévérons dans cette stratégie, non seulement nous nous récompenserons, mais nous continuerons à monter.

Bien sûr, le résultat final de ces stratégies doit être nul et sans retour. Mais non seulement sans retour, mais aussi avec une forte sensation de douleur de la perte d’un rêve.

J’ai vu cela plus d’une fois. Chaque fois que quelqu’un me fait part d’une nouvelle idée de transaction qui n’est presque pas retirée, je me demande si ce n’est pas une autre erreur de la part d’un joueur.

Les gens qui s’y adonnent, souvent sans pouvoir s’en sortir, les soi-disant stratégies de négociation de grilles, la méthode de la Martingale, etc., ne peuvent jamais échapper aux griffes de l’erreur des banquiers, mais elles peuvent nécessairement acquérir une vitalité immortelle.

Parce que ce qui détermine la popularité d’une tactique, ce n’est jamais sa capacité à gagner, mais si elle est adaptée à l’humain.

Il semble que tout ce qui existe dans le monde, tant qu’il répond aux attentes de la nature humaine, obtient une vitalité tenace. Comme dans l’escroquerie de Ponzi. La stratégie de la grille est bonne, la stratégie de la Martingale est bonne, elle vous donne toujours un retour très très stable au début.

Le cerveau humain déteste les pertes bien plus que les gains. C’est une tactique que les ancêtres de l’humanité ont évoluée dans les temps anciens, parce que les ancêtres des prairies n’avaient pas le temps de penser à quelque chose de trop loin, de se remplir le ventre et de finir le repas.

Cependant, la civilisation de l’humanité a évolué rapidement, de jour en jour, le cerveau au sens biologique, a encore évolué en unités de millions d’années. Comment un cerveau ancien peut-il faire face aux marchés financiers d’aujourd’hui? Ne jugez donc pas le marché et les stratégies en fonction de vos propres sentiments subjectifs; vous devez vous fier aux connaissances humaines, pas aux sentiments.

Les chercheurs de l’Université de Montréal ont publié une étude sur la neuroéconomie, qui a été publiée dans la revue Neuroeconomics.

Si vous avez été recommandé par quelqu’un pour une stratégie de trading sûre et sans perte, et que le promoteur est convaincu qu’il n’a pas besoin d’avoir une idée précise du marché pour faire de la gestion de votre argent une règle de base de trading.

Les marchés financiers sont un peu comme des systèmes de thermodynamique, et il est important de garder à l’esprit les conclusions de la thermodynamique pour éviter d’être trompé.

Le plus important est la loi de la conservation de l’énergie, l’énergie n’est pas créée par rien et ne disparaît pas par rien. Sur le marché, il est impossible de faire des bénéfices par rien si vous ne faites pas de contributions ou de connaissances, et si vous ne faites pas du marché une ressource plus efficace, ce qui est contraire aux lois de la nature.

Il n’y a pas de stratégie qui puisse contrevenir aux lois de la nature, c’est une certitude. Toute stratégie qui fonctionne doit avoir utilisé l’asymétrie de l’information, ou avoir une vision surhumaine, ou utiliser ses propres ressources pour rendre le marché plus efficace.

La stratégie de négociation de la grille ((le mauvais est de doubler et d’augmenter le risque), le désir de ne fournir aucune sortie et de gagner des bénéfices, c’est comme si l’on voulait fabriquer un moteur à perpétuité, c’est forcément un rêve de fou.

Sans tenir compte du coût de la transaction, le rendement attendu de la stratégie de grille est de zéro.

Ce rendement attendu de zéro est purement mathématique, et compte tenu du coût de la transaction, le rendement attendu est négatif, c’est-à-dire une stratégie de perte forcée.

Encore une fois, étant donné que la stratégie de la grille dit que les investissements supplémentaires nécessaires sont conformes au modèle de rentabilité, après plusieurs erreurs, les nouveaux investissements nécessaires seront astronomiques.

La capacité de financement est finalement limitée, et la présence de cette contrainte implique des résultats moins intéressants.

Tout le monde est raisonnable, persévérant, mais si difficile.

Mais mais !!! Après avoir dit qu’il n’y avait pas de pain dans le ciel depuis si longtemps, tout le monde avait l’air déçu, après avoir compris l’erreur des joueurs, voyons ce que les sages du jeu d’échecs ont dit.

Le blogueur a commenté sur Twitter:

Un jeu apparemment simple et équitable: un simple dispositif mécanique, avec deux embouchures de pièces de monnaie, représentant respectivement le noir et le blanc. Les joueurs y jettent les pièces de jeu correspondantes (équivalent en espèces de 1 dollar).

En parlant de S, je me rends compte que le pari est l’équivalent de dire que le patron a une probabilité de 1 pour un événement mutuellement exclusif de ¹⁄₂. Dans ce modèle, le gain attendu est toujours égal à zéro, quel que soit le mélange de stratégies que les joueurs utilisent.

Je ne sais pas comment gagner, je ne pense pas que ce soit possible.

Sjun poursuit en disant que sa stratégie est très simple: chaque fois qu’il choisit une couleur, comme le noir, il met une pièce de monnaie sur le noir pour la première fois; s’il perd, il met deux pièces de monnaie sur le noir pour la deuxième fois; s’il perd encore, il met quatre pièces de monnaie sur le noir pour la troisième fois… et ainsi de suite. Si n tours ne gagnent pas, il met 2 pièces de monnaie sur le noir pour la n + 1e tour.

L’avantage de cette méthode est que, quelle que soit la perte de l’argent précédent, si vous gagnez la prochaine fois, vous pouvez récupérer votre perte en argent, un dollar net, et la probabilité de n échecs consécutifs est très faible, seulement 1/(2 ^ n).

Bien sûr, cette approche ne me suffit pas. Quand j’ai dit que les attentes de toute stratégie de confusion étaient nulles, cela incluait naturellement cette stratégie.

Cette stratégie semble avoir une faible probabilité de défaite, pourquoi s’attendre à zéro ? C’est simple, parce que son pari est trop gros, en supposant qu’il ait perdu les 7 premières fois, il devra faire un pari de 256 dollars à la huitième fois avant de pouvoir revenir. Mais à la huitième fois, il perd 511 dollars, et je ne pense pas que le débutant S ait le capital de continuer à perdre. En d’autres termes, bien que la probabilité de défaite soit faible, la perte de chaque événement de petite probabilité de sept ou huit défaites est également mortelle, ce qui lui permet de ne pas avoir d’argent pour continuer à jouer pendant plusieurs semaines.

Pour être honnête, j’ai de sérieux doutes sur la viabilité de cette stratégie.

En arrivant ici, nous pouvons voir que c’est une stratégie aussi simple que la stratégie de la grille, une forme classique de l’erreur des gangsters.

Cependant, en fait, S-jun a effectivement utilisé cette stratégie, après avoir gagné 20 à 30 pièces de monnaie dans la salle de jeux, il est allé jouer à d’autres jeux pendant une longue après-midi. Non seulement je crois totalement à ses paroles, mais son analyse ultérieure m’oblige à croire que cette stratégie fonctionne, car mon analyse précédente a été fatalement erronée.

Tu as fait une erreur fatale, Yang Hanping, en croyant que c’était un jeu parfaitement équitable.

C’est là qu’intervient l’idée intéressante, le super dry. (Les traders de Londres recommandent de lire attentivement)

Que voulez-vous dire par là ?

Sjun sourit et dit: “Votre analyse est mathématiquement irréfutable. Mais n’oubliez pas que votre conclusion est que les attentes du joueur sont nulles, en d’autres termes, les attentes du propriétaire sont nulles aussi. Mais le revenu du propriétaire est-il vraiment nul, et s’il est nul, n’a-t-il pas payé le loyer pour acheter cette machine ?

En fait, j’ai aussi pensé à l’idée de M. S. que le joueur gagnerait forcément de l’argent. La seule façon de le faire est de manipuler la petite balle. Faire une hypothèse extrême, si quelqu’un joue 10 000 en blanc, sa probabilité de gagner est très faible, le joueur ne regardera pas le courant de l’est pendant plusieurs semaines. Bien que personne ne gagne 10 000 dans la salle de machines à sous, mais selon M. S., il n’est pas rare que des adultes gagnent 200-300 dollars à la fois.

Pour le joueur, la situation la plus cupide est de manipuler la boule pour qu’elle tombe sur la couleur la moins mise et qu’elle gagne à chaque fois. Mais ce n’est pas la norme, et si c’est trop évident et que le joueur s’en rend compte, ce n’est pas un jeu agréable.

Le joueur devrait avoir des gains et des pertes, et maintenir un petit profit adéquat, par exemple 10% sur dix tours, ce qui n’est pas énorme, mais c’est un profit énorme par rapport aux produits financiers et immobiliers.

J’ai un doute: pour les joueurs, c’est pas votre stratégie de prendre parti pour une minorité à chaque fois ?

S poursuit en disant que la machine est configurée de telle sorte que chaque joueur lance une pièce à l’avant. Sans communication avec le joueur, il est essentiellement impossible de voir les autres joueurs lancer la pièce à cet endroit, et il est impossible de communiquer avec les autres joueurs et de prendre des décisions à chaque fois.

Moi: Alors, vous avez gagné en minorité, et cette règle de plongée sous-marine n’a pas de sens pratique ?

S: Tu ne peux pas le voir de cette façon. En fait, quand tu te rends compte que le jeu existe, tu es déjà beaucoup plus avancé que tu ne l’étais avant.

Moi: Il y en a d’autres, je pense que quelques victoires suffisent à faire gagner de l’argent au patron.

S: Le patron de la loterie a déjà pris en charge le coût de la machine et du terrain, c’est-à-dire qu’il est redevable pour ce jeu. Non seulement il ne peut pas être débiteur, mais il doit aussi gagner de l’argent.

Moi: Pour les joueurs, c’est un jeu qui n’a pas de taxes, qui a l’air de gagner à moitié, et qui est déjà très tentant.

S: Eh bien, mais les autres joueurs qui n’ont pas une mentalité mathématique ne voient pas les choses de cette façon.

Moi: Oh oui, bien que la probabilité d’échec soit de 1 sur 2^n, mais une fois que l’échec a eu lieu, il y a une perte de 2^n environ et les attentes globales sont toujours de zéro.

S: Eh bien, vous devriez réfléchir à la possibilité que j’échoue. J’ai généralement environ 300 yuans, ce qui suffit à me soutenir de la première mise à 128 yuans, soit huit jeux. La seule possibilité que j’échoue est que huit jeux consécutifs soient blancs, et j’ai fini.

Moi: Oh, bien que cela soit peu probable, c’est vrai… et les pertes sont énormes…

S: Vous vous trompez, cette probabilité n’existe que dans les mathématiques. En fait, il n’y a aucune possibilité que le patron ne permette pas que cela se produise. Imaginez que dans le jeu, une fois que huit fois la même couleur apparaît, pour moi, c’est bien acceptable, car j’ai joué des milliers de fois, huit fois la probabilité de blanc est de ¹⁄₁₂₈, toujours rencontré. Mais pour les autres joueurs qui ont joué seulement une fois de temps en temps, qu’est-ce qu’ils penseraient, sont-ils prêts à accepter qu’ils ont heurté la chance de ¹⁄₁₂₈, ou commencent-ils à remettre en question le croupier?

Le but n’est pas de faire en sorte que les joueurs ne se demandent pas si le jeu est manipulé, mais de leur donner l’impression qu’ils ne le sont pas.

Sur la base de ce principe, même les événements de faible probabilité dans une distribution normale doivent être supprimés, car ils peuvent être remis en question (parce que l’équité est injuste). Au contraire, la manipulation occasionnelle de plusieurs plateaux à la cuisson à l’eau chaude de la grenouille donne la victoire à une minorité, car le joueur ne sait pas à l’avance que le blanc et le noir sont minoritaires, et ne perturbe donc pas la distribution moyenne du noir et du blanc.

C’est pourquoi le joueur n’hésite pas à laisser quelques-uns gagner, car cette ruse ne brise pas l’équilibre intuitif entre le noir et le blanc. Mais il est absolument interdit de laisser apparaître plusieurs couleurs de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur de la même couleur, même si cette petite probabilité devrait se produire dans un grand nombre de jeux.

Ce sont des événements de faible probabilité en mathématiques qui sont modifiés en réalité pour être des événements de probabilité zéro.

C’est à ce moment que j’ai vraiment compris où S est vraiment doué et pourquoi une stratégie aussi simple gagne toujours dans un jeu aussi équitable.

Plus tard, S ajoute qu’il pense qu’il est trop compliqué pour le patron de contrôler délibérément 10% des revenus, car il doit s’occuper des autres jeux et joueurs. Donc, il est plus proche de la réalité que la machine elle-même a une distribution aléatoire. Dans cette distribution, les revenus du patron sont effectivement les mêmes que ceux du joueur dans son ensemble, soit zéro.

La stratégie de S n’est pas seulement efficace pour les patrons cupides, elle est également expérimentée pour les machines apparemment équitables. La raison est simple, c’est une machine d’il y a dix ans, qui a bien des composants électroniques à l’intérieur, mais c’est plus un simple dispositif mécanique. En fait, personne, y compris un ordinateur, ne peut créer une machine qui exprime réellement le hasard.

Mais pour une simple machine, il est très coûteux de simuler des dizaines de situations, et il n’est pas nécessaire de supposer que la machine ne stocke que le noir et le noir, le noir et le noir, le noir et le noir, le noir et le noir, le noir et le blanc, le noir et le blanc, le noir et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc, le blanc et le blanc et le blanc, le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le blanc et le

Pour S, si la machine n’enregistre que ces 32 cas et les appelle à plusieurs reprises, sa stratégie est toujours gagnante, pourvu qu’elle soit prête à parier cinq fois: 1+2+4+8+16=31 yuans.

En fait, S a acheté plus de 30 pièces de monnaie lors de son premier retrait. Chaque fois qu’il utilise ces pièces comme capital, il gagne 20 à 30 pièces de monnaie supplémentaires pour jouer au jeu qu’il veut vraiment jouer.

C’est à ce moment-là que j’ai réalisé à quel point j’étais éloigné de S. Tous mes jugements étaient basés sur des mathématiques, et c’était une partie de la pensée que j’avais résolue avec les deux ou trois cents mots précédents, mais les milliers de mots suivants étaient le domaine dans lequel S pensait vraiment.

J’ai vu cette vidéo pour la première fois et j’ai été comme un bébé qui a été sevré et remplacé par un os !

Après tout, en jouant avec les gens, j’ai été jusqu’à présent dans le monde quantifié des chiffres, à la recherche de stratégies pour espérer des gains plus élevés, et j’ai négligé un fait fondamental qui est immédiatement visible:

La spéculation est un jeu avec des êtres vivants ! La quantification n’est jamais qu’un moyen et une méthode, les traders font des transactions avec des êtres humains. Ce que l’on appelle une transaction, c’est une transaction effectuée avec un contrepartie et vous.

Il n’est pas difficile de comprendre les paroles suivantes.

S dit qu’il y a parfois des urgences ou d’autres raisons pour lesquelles il n’a pas eu le temps d’économiser les pièces de jeu et qu’il doit rentrer chez lui. Il demande rarement à son patron de changer les pièces restantes en argent (en principe possible). Mais compte tenu du fait qu’il doit répéter cette stratégie, il ne peut pas être avide de petits bénéfices et laisser son patron soupçonner qu’il choisira une pièce de jeu mathématiquement évidente qui perdra rapidement. Bien sûr, il gagnerait de temps en temps jusqu’à ce que le premier magasin s’effondre soudainement, plus de 30 pièces de jeu sur le bouton, et gagnerait une douzaine d’argent, après tout, c’est principalement pour le plaisir, pas pour gagner de l’argent.

C’est le cas de S.

S, le plus intelligent, comprend parfaitement l’avantage de l’information que possède le patron, le propriétaire du casino, qui est l’opposant, a le pouvoir d’arrêter le jeu, et la stratégie la plus intelligente est de se faire plaisir.

Ce n’est qu’en étant au niveau supérieur que vous pourrez surpasser vos adversaires, et ce n’est qu’en ayant une vision différente que vous pourrez tirer profit.

Le désir d’un profit sans effort est la cause fondamentale de la tromperie.

Est-ce qu’il y a une stratégie de profit dans le monde qui ne juge pas les mouvements des prix ?

Oui, mais ils réussissent parce qu’ils contribuent, pas parce qu’ils gagnent.

Pour donner un simple exemple, l’or de Londres, l’or de New York et l’or de Shanghai ont exactement les mêmes propriétés chimiques.

Mais comme les deux sont négociés sur des bourses différentes, il en résulte une stratégie appelée arbitrage intermarché. Cette stratégie utilise la loi du prix unique, qui veut dire qu’il ne peut y avoir qu’un seul prix pour la même chose au même moment.

Les institutions qui ont un avantage de négociation, utilisent leur avantage sur l’informatique et le capital pour prévenir les écarts de prix, faire court sur l’or à prix élevé et faire des produits d’or à prix relativement bas. Pour les méthodes d’arbitrage sur la technologie informatique et les stratégies de haute fréquence, voir l’article sur les chasseurs de Wall Street.

Si le prix revient, ce portefeuille sera rentable, sans se soucier de la hausse ou de la baisse future de l’or, il sera rentable. (Si l’or augmente à l’avenir, il est préférable de faire plus d’argent à bas prix que de perdre des positions à bas prix, et vice versa.)

Parce que l’agence a dépensé ses ressources pour aider le marché à être plus efficace et a ainsi obtenu le retour qu’elle méritait.

En effet, vous n’avez pas mangé du pain qui vient du ciel, comme je l’ai annoncé.

Comme les traders londoniens le soulignent à maintes reprises: si vous ne savez pas ce qu’est une entreprise, où sont vos atouts, pourquoi quelqu’un a besoin de vous, où est votre plafond, pourquoi elle ne vous rapporte pas de profit, alors ne la faites pas.

Il vaut mieux ne pas faire de transaction sans en avoir la certitude, que de la faire à temps. Bien sûr, si vous avez déjà fait une transaction, il y a un problème, ou la faire à temps, c’est une condition de survie.

• ### Pour résumer:

Ne croyez pas que les soi-disant bonus et retours de position génèrent de véritables bénéfices, à moins que vous n’ayez une idée de l’origine de la fraude de Panche.

Il y a toujours un doute dans l’esprit de toute promesse de taux d’intérêt élevé.

Comme pour la stratégie de grille, il n’y a pas de stratégie de retrait, il faut être prudent. Pourquoi un tel résultat, quel est son avantage ?

Si vous n’avez pas d’idées ou de ressources extraordinaires, le marché vous les rendra.

(Créé par le traders de Londres)