Ratio de Sharpe 0,6, dois-je l’abandonner ?

Nous faisons une expérience pour illustrer ce problème. Cette expérience commence par quelques hypothèses cruciales. Nous avons 20 signaux de transactions avec un rendement annuel composé de 8% et un Sharpe ratio annuel de 0.6. Les signaux de cette stratégie ne sont pas très productifs.

• Une variable d’entrée importante dans la négociation est la corrélation entre les signaux. Nous menons une série d’expériences selon un coefficient de corrélation de 0 à 0.9. Les expériences ne tiennent pas compte du coût de la négociation (car nous ne sommes intéressés que par le rendement relatif) et la distribution du rendement annualisé du portefeuille rééquilibré quotidiennement en fonction de la corrélation est fondamentalement la même.

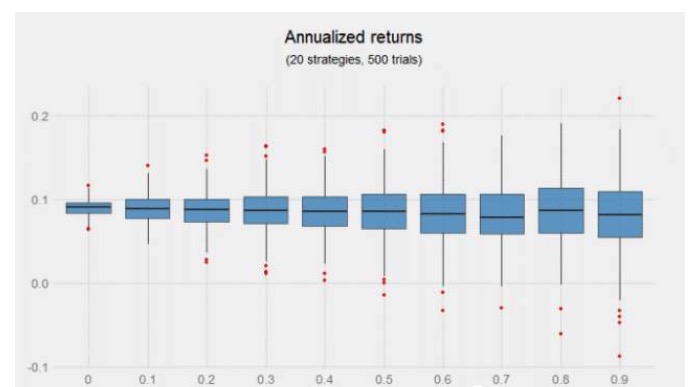
La combinaison de signaux de faible corrélation n’augmente pas le rendement, mais le graphique ci-dessus suggère les avantages que peuvent apporter les stratégies d’augmentation, en particulier lorsque ces stratégies ne sont pas correlatrices. La moitié gauche du graphique, c’est-à-dire le coefficient de corrélation de 0 à 0,4, est plus étroitement répartie et le rendement des cinq cents expériences est positif.

Les résultats sont plus clairs lorsque l’on utilise le Sharpe ratio pour mesurer les bénéfices ajustés au risque. Si 20 stratégies avec un Sharpe ratio annualisé de 0,6 et un coefficient de corrélation de 0 forment un ensemble, le Sharpe ratio annualisé est de 3, alors que 20 stratégies avec un Sharpe ratio annualisé de 0,6 et un coefficient de corrélation moyen de 0,9 forment un ensemble avec un Sharpe ratio annualisé de 0,64, la première génère un rendement supérieur de 370% à celui de la seconde.

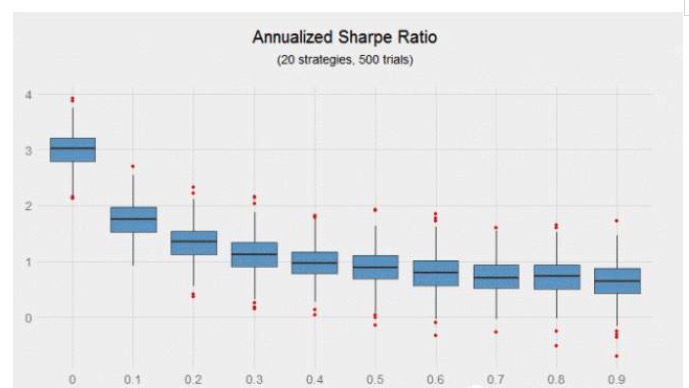
Ce qui est remarquable dans le graphique ci-dessus, c’est que le taux de Sharpe diminue rapidement à mesure que la pertinence de la stratégie augmente. En augmentant le coefficient de pertinence de 0 à 0,2, le taux de Sharpe diminue de 56%.

Même avec un Sharpe ratio élevé, la stratégie de portefeuille a près de 50 000 signaux de transaction, la différence de Sharpe ratio de portefeuille avec une corrélation de zéro est étonnante. Un investisseur chanceux peut obtenir un Sharpe ratio de 3.5 (qui peut faire de quelqu’un un milliardaire) et un investisseur malchanceux qui détient le même portefeuille n’obtient qu’un Sharpe ratio de 2.5. Même avec un portefeuille à haut Sharpe ratio, la chance joue un rôle important.

Il est évident que plus il y a d’échantillons d’observations, plus les frontières deviennent claires. Que se passe-t-il si un investisseur n’observe qu’un échantillon d’observations d’un an au lieu d’un échantillon d’observations d’une décennie?

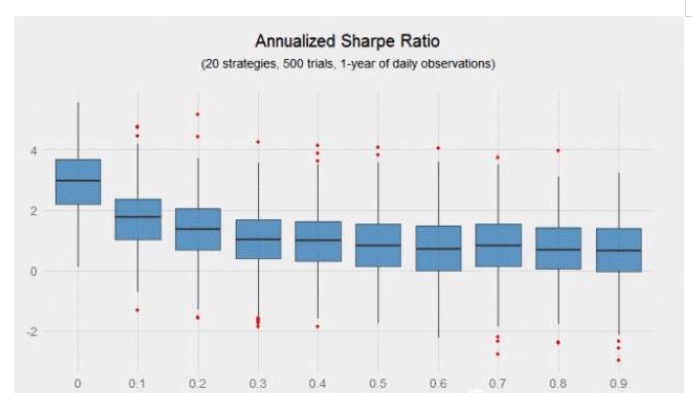
Si nous simulons les 10 000 stratégies individuelles mentionnées ci-dessus, quelle proportion de la p-value est inférieure à 5%? La réponse est proche de 48%, ce qui pourrait amener la plupart des chercheurs à abandonner une telle stratégie quotidienne (c’est-à-dire une stratégie avec un rapport Sharpe annualisé de 0.6). Cependant, si la corrélation entre les signaux est suffisamment faible, la combinaison de ces signaux faibles peut produire des miracles et le flux de rendement de la combinaison devient très significatif.

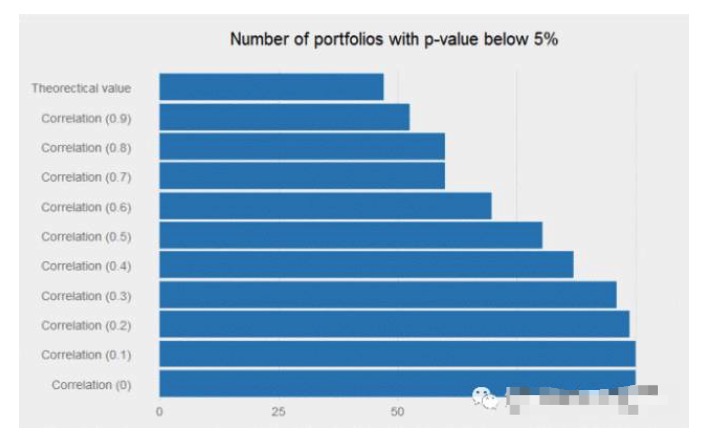
Une stratégie avec un Sharpe ratio annualisé de 0,6 peut être rejetée par les chercheurs car elle n’a aucun attrait dans le trading. Cependant, si elle a une corrélation correcte (c’est-à-dire faible) entre les signaux existants, elle peut très bien augmenter la valeur du portefeuille.

Cet article n’ouvre pas de nouveaux domaines, car les avantages de la diversification sont bien connus dans le monde de l’investissement. Mais il vous rappelle qu’il n’est pas nécessaire d’abandonner une stratégie de SHARP annualisé de 0,6.

La vidéo a été postée sur le site de l’entreprise.