Couverture Delta des options Bitcoin à l’aide de la Smile Curve

résumé

Nous analysons la couverture dynamique robuste du delta des options Bitcoin à l’aide d’un ensemble de courbes de sourire implicites et d’autres deltas ajustés au sourire. Ces deltas sont soit sans modèle, dans le sens où ils sont les mêmes pour chaque modèle stochastique et/ou de volatilité locale invariant à l’échelle, soit ils sont basés sur de simples paramétrisations de volatilité locale dépendantes du régime. Ces deltas sont populaires parmi les teneurs de marché sur les marchés d’options pour les actifs traditionnels car ils sont faciles à mettre en œuvre. Les recherches empiriques antérieures sur la couverture delta dynamique se basaient uniquement sur les options sur indices boursiers, mais l’analyse de données uniques sur les prix historiques horaires des options Bitcoin montre que le comportement de la courbe de volatilité implicite de Bitcoin est très différent de celui des options sur indices boursiers. Pour les options d’achat et de vente avec un large univers de financement et des échéances fixes synthétiques de 10, 20 et 30 jours, nous comparons la performance de couverture dynamique de différents deltas ajustés au sourire sur deux périodes d’un an. Nous étudions également l’utilisation de contrats perpétuels plutôt que de contrats à terme standard comme instrument de couverture, car le risque de base des contrats perpétuels est bien inférieur à celui des contrats à terme calendaires. Les résultats sont présentés sous la forme d’une statistique testable du ratio de variance d’erreur couverte. Sur certaines périodes, l’utilisation du ratio de couverture implicite de la courbe du sourire peut considérablement surpasser la simple couverture Delta Black-Scholes, en particulier lors de l’utilisation de swaps perpétuels comme outil de couverture, le gain d’efficacité des options de vente hors de la monnaie peut dépasser 30 %, Lors de la couverture d’options d’achat à court terme hors de la monnaie pendant les périodes de courbes de volatilité implicite ascendantes, les gains d’efficacité moyens peuvent atteindre 15 %. Les avantages de l’utilisation de contrats perpétuels sont particulièrement évidents en 2021, notamment pour les contrats à long terme où la base est encore assez large.

Mots clés ：Couverture des produits dérivés, courbe de volatilité implicite, contrats perpétuels, financement robuste, couverture incrémentale dynamique

1. Introduction

Toute recherche sur la couverture delta dynamique est basée sur le modèle de Black et Scholes (1973). Le delta Black-Scholes (BS) ne nécessite que des dérivées partielles du prix de l’option du modèle par rapport au prix sous-jacent, puisque le modèle suppose que la corrélation entre le prix sous-jacent et sa volatilité est nulle. Cependant, il est bien connu que les options sur indices boursiers présentent une corrélation prix-volatilité importante et négative, ce qui conduit à une asymétrie significative de la courbe de volatilité implicite. Suivant l’idée de base de Bates (2005) et les résultats plus généraux d’Alexander et Nogueira (2007a), la pente de la courbe de volatilité implicite peut être utilisée pour impliquer des ajustements au BS Delta, qui est sans modèle, c’est-à-dire, elle est constante pour toute échelle indépendante. Les modèles variantes sont les mêmes. Cependant, Alexander et Nogueira (2007b) montrent que pour les instruments négociables (autres que les taux d’intérêt), chaque modèle de tarification d’options sur actions à volatilité stochastique et/ou locale devrait être invariant d’échelle, quels que soient les facteurs supplémentaires tels que les sauts ou les processus de Lévy. les caractéristiques sont. Par conséquent, toute différence entre les performances de couverture empiriques des deux modèles de volatilité paramétrique (pour les instruments négociables) est simplement due au fait que les modèles présentent des erreurs d’étalonnage différentes. La dérivée partielle delta (en fait gamma) du prix de l’option par rapport au prix de l’instrument négociable est théoriquement exactement la même que le delta invariant d’échelle sans modèle. Remarque 1 De plus, le Delta simple invariant à l’échelle proposé par Bates (2005) est plus grand (plus petit) que le Delta BS lorsque la pente de la courbe du sourire est négative (positive). Étant donné que Coleman et al. (2001) montrent que le delta BS a tendance à être sur-couvert dans un cadre de volatilité locale, lorsque la volatilité implicite est négativement biaisée, le delta invariant d’échelle sera plus sur-couvert que le delta BS.

Comme décrit par Alexander et Nogueira (2007a), la dérivée totale de variance minimale (VM) par rapport au prix est un autre delta qui prend en compte les corrélations prix-volatilité non nulles, mais elle dépend du modèle. Cependant, ces auteurs n’ont pas été en mesure de faire la distinction entre les résultats empiriques obtenus en utilisant le MV Delta sans modèle de Lee (2001) et le MV Delta basé sur différents modèles invariants d’échelle. Le delta MV de Lee (2001) est également « ajusté en fonction du sourire », c’est-à-dire qu’il ajoute un terme au delta BS qui est calibré à l’aide des caractéristiques empiriques de la courbe de sourire de volatilité implicite. Une autre façon d’ajuster le BS Delta est d’utiliser l’approche proposée dans le travail fondateur de Smile-Adjusted Delta de Derman et Kani (1994) et Derman (1999) en ajoutant un terme qui capture la corrélation prix-volatilité. Ceux-ci ne sont pas totalement indépendants du modèle, puisque le terme d’ajustement dépend de la paramétrisation de la volatilité locale, qui dépend elle-même du régime en vigueur sur le marché. Cependant, ils sont dépourvus de modèle dans la mesure où aucune hypothèse n’est faite sur les processus qui déterminent l’évolution du prix sous-jacent, comme la diffusion des sauts de volatilité locale stochastique, et il n’y a pas de paramètres qui doivent être calibrés à l’aide des prix des options et/ou des données historiques sous-jacentes. données.

Il est courant pour les teneurs de marché d’options sur actions de couvrir leur exposition en utilisant de simples ajustements sans modèle du BS Delta, car ceux-ci sont considérés comme ce que l’on appelle un « financement robuste », c’est-à-dire que le ratio de couverture est indépendant du modèle. Les courbes de sourire implicites et autres haies delta ajustées en fonction de la courbe du sourire sont particulièrement populaires parmi les praticiens, comme en témoignent de nombreux articles et forums. Remarque 2 : Il existe plusieurs études empiriques antérieures sur la couverture delta des courbes de sourire implicites et/ou des courbes ajustées au sourire, mais elles ont toutes étudié les options sur indices boursiers. Tous les résultats ne sont pas cohérents : Vähämaa (2004) montre que certains deltas ajustés par la courbe souriante surpassent les deltas BS pour les options FTSE 100, mais seulement pendant les périodes de volatilité excessive ; Crépey (2004) confirme que ces résultats s’appliquent aux options DAX 30 ; Attie ( (2017) affirme que le delta implicite du sourire surpasse systématiquement le delta BS dans la couverture des options de l’indice S&P 500 ; Alexander et al. (2012) étendent le cadre de Derman (1999) à un paramètre de commutation de Markov. pour refléter le delta ajusté correct du sourire applicable au marché actuel régime de marché, montrant que pour les options S&P 500, le BS Delta ne peut être amélioré qu’en utilisant cette extension de commutation de Markov ; François et Stentoft (2021) ont également étudié les options de l’indice S&P 500 et confirment que les ajustements standards ne peuvent pas surpasser le BS delta ou le delta-gamma haies, mais leur nouvelle courbe souriante implicite delta-gamma-vega améliore considérablement le modèle BS. On sait peu de choses sur le succès de la couverture delta ajustée au sourire par rapport aux autres types d’options. Note 3

L’objectif de cet article est d’examiner les performances de couverture delta de diverses courbes implicites Smile et d’autres courbes ajustées Smile appliquées aux options Bitcoin. Au moment de la rédaction de cet article, seule une petite quantité de recherches a été publiée sur les options Bitcoin. Siu et Elliott (2021), Jalan et al. (2021) et Chen et Huang (2021) étudient tous les applications empiriques des modèles de tarification de la volatilité stochastique, mais aucun des articles n’étudie leurs performances de couverture. Hou et al. (2020) ont considéré une série de modèles de volatilité stochastique pour évaluer les options Bitcoin. Les auteurs présentent un ensemble de résultats importants qui soulignent l’importance des sauts et des co-sauts et proposent un modèle de volatilité stochastique avec sauts corrélés (SVCJ) pour évaluer les options Bitcoin. Ces modèles sont très utiles pour évaluer les options exotiques telles que les options à cliquet ou à cliquet. Bien que Chi et Hao (2021) considèrent les stratégies de couverture delta basées sur GARCH, leurs recherches se concentrent sur la comparaison de différents modèles de prévision de la volatilité réalisée. Alexander et al. (2022b) étudient le comportement de la courbe de sourire de volatilité implicite pour les options Bitcoin afin de déduire si la pression de la demande des teneurs de marché est motivée par les traders directionnels ou les traders de volatilité. En fait, à notre connaissance, il n’existe qu’une seule autre étude détaillée sur les options de couverture Bitcoin (Matic et al., 2021), et elle utilise une approche complètement différente de celle de cet article. Matic et al. (2021) utilisent la volatilité implicite quotidienne cotée par la bourse Deribit pour calibrer la surface de volatilité implicite inspirée de la volatilité stochastique paramétrique, puis interpolent la volatilité implicite des options entre un et trois mois sans arbitrage. Volatilité. L’échantillon entre avril 2019 et mars 2020 est ensuite divisé en trois sous-périodes (marché haussier, marché calme et période COVID) en utilisant le processus de volatilité stochastique introduit par Duffie et al. (2000) et McNeil et Frey (2000). Densité du noyau de filtre GARCH pour modéliser les prix sous-jacents des crypto-monnaies. Ils comparent ensuite la performance de couverture des BS Grecs avec celle dérivée de divers modèles de saut de volatilité stochastique. Pour les options avec une expiration d’un mois, les auteurs ne trouvent pas d’améliorations significatives par rapport à la simple couverture BS, mais pour les options avec une expiration de trois mois, des modèles plus complexes améliorent considérablement les performances de couverture.

Contrairement à Matic et al. (2021), nous ne comparons pas les performances de couverture des options de différents modèles de volatilité stochastique. Un avantage pratique important de notre étude est que toutes les valeurs Delta sont très faciles à calculer. Étant donné que toutes les informations sont dérivées de la courbe de volatilité Smile de manière directe et robuste, sans modèle, aucun étalonnage du modèle n’est requis. Résultats de notre couverture delta utilisant différents ajustements BS Delta qui dépendent des conditions actuelles du marché, de la forme du sourire de volatilité implicite et/ou de la corrélation prix-volatilité.

Nous nous concentrons sur les options à court terme avec des échéances de 10 à 30 jours, qui présentent une liquidité beaucoup plus élevée et une gamme de prix d’exercice plus large que les options étudiées dans Matic et al. (2021). Nous avons choisi de procéder ainsi car les options Bitcoin avec des dates d’expiration comprises entre un et trois mois ne représentent que 20 % du volume total des transactions, tandis que les options avec des dates d’expiration de 30 jours ou moins représentent 50 % du volume total des transactions. Environ 80 % de toutes volume des échanges. De plus, nous avons besoin d’une courbe de sourire appropriée pour ajuster le BS Delta, et la plage de frappe liquide de ces options à court terme est assez large. En fait, le rapport entre la valeur monétaire des options utilisées dans notre analyse empirique varie de 0,7 à 1,3.

Nous examinons uniquement la couverture delta dynamique avec un rééquilibrage régulier, qui se produit toutes les huit heures au moment du financement ou quotidiennement à 00h00 UTC. Le choix de ce modèle expérimental est basé sur les caractéristiques du marché des options Bitcoin, qui sont nouvelles et donc expliquées en détail plus tard. Les coûts de transaction des contrats à terme sont bien inférieurs à ceux des options. Par exemple, les contrats à terme ont des spreads allant d’environ 1 à 5 points de base, selon la date d’expiration, mais les options à cours limité à court terme, qui sont souvent utilisées pour la couverture gamma, ont généralement des spreads d’environ 200 à 300 points de base. points. Par conséquent, la couverture gamma est beaucoup plus coûteuse que la couverture delta dynamique classique. Les coûts de transaction liés au rééquilibrage d’une couverture gamma peuvent éroder tout profit réalisé en réduisant l’erreur de couverture, alors que les coûts de transaction liés au rééquilibrage d’une couverture delta sont faibles, en particulier lorsque des contrats perpétuels sont utilisés comme instrument de couverture.

Ensuite, la section 2 décrit le marché des options et des contrats à terme sur Bitcoin ; la section 3 compare les caractéristiques des surfaces de volatilité implicite pour Bitcoin et les indices boursiers et distingue leurs caractéristiques ; la section 4 décrit notre cadre empirique. Chaque ratio de couverture est présenté sous la forme d’une formule BS ajustée ; La section 5 décrit nos données ; la section 6 présente les résultats empiriques ; et la section 7 conclut.

2. Options et marchés à terme sur Bitcoin

Au moment de la rédaction de cet article, six grandes bourses de crypto-monnaies proposent des options de trading en Bitcoin et dans d’autres devises, ainsi que sur certains jetons, avec un volume moyen quotidien total de transactions approchant 1 milliard de dollars en décembre 2021. En particulier, le volume des transactions sur les options Bitcoin a récemment atteint des sommets historiques, avec un volume mensuel moyen de transactions plus que doublé et un intérêt ouvert augmentant de plus de six fois de janvier 2020 à décembre 2021. La grande majorité des transactions se déroule sur la bourse d’options Deribit, qui a été délocalisée au Panama pour éviter de suivre les normes internationales établies par des agences gouvernementales telles que la Commodity Futures Trading Commission (CFTC) des États-Unis ou toute autre forme de réglementation visant à protéger les intérêts des clients. Comme de nombreuses autres bourses de produits dérivés de crypto-monnaie non réglementées, souvent enregistrées dans des paradis fiscaux offshore, la plateforme de trading de Deribit est ouverte 24h/24 et 7j/7 et adhère à peu ou pas de protocoles de « connaissance du client ». 4,3 millions de contrats (d’une valeur notionnelle d’environ 55 milliards de dollars) ont été négociés sur Deribit en 2020, et 6,2 millions de contrats (d’une valeur notionnelle d’environ 290 milliards de dollars) ont été négociés en 2021. En conséquence, en seulement deux ans, le nombre de contrats cotés a augmenté de plus de 45 % et le montant notionnel négocié sur Deribit a augmenté de plus de 430 %. Note 4 Pour mettre cela en perspective, le marché des options S&P 500 du Chicago Board Options Exchange (CBOE) n’a augmenté que d’environ 10 % entre 2020 et 2021. Note 5 Sur le marché des options Bitcoin, de nouvelles tailles de contrat, des fourchettes de prix d’exercice plus larges, des échéances plus longues et de nouveaux sous-jacents sont publiés presque chaque mois, élargissant ce marché émergent des produits dérivés aux traders particuliers et institutionnels. Faire des options Bitcoin plus qu’un simple produit de niche . En mars 2022, le Chicago Mercantile Exchange (CME) a ​​lancé des options micro Bitcoin pour tenter de concurrencer les plateformes autorégulées ciblant les traders de détail. Mais les grands acteurs institutionnels surveillent également de très près le marché des options, certains le qualifiant même de « prochaine grande étape ». Note 6 D’autre part, les protocoles émergents de finance décentralisée (DeFi) comme Opyn ou Ribbon Finance proposent des options de trading sans suivre aucune conformité réglementaire. Avec un volume d’échange notionnel de plus de 500 millions de dollars par jour, ce n’est plus un marché que les investisseurs traditionnels peuvent ignorer.

Le volume considérable des échanges sur Deribit en fait la bourse la plus attractive pour tout type de recherche d’options de crypto-monnaie. Même si CME (et certaines autres bourses) ne répertorient que les options Bitcoin, seulement 10 à 15 % du volume de transactions d’options Bitcoin peut être attribué à ces bourses. Deribit représente à lui seul plus de 90 % du volume des transactions d’options Bitcoin. Note 7 Une raison pourrait être que Deribit fonctionne 24 heures sur 24, 7 jours sur 7, tandis que CME ne fonctionne qu’en semaine. Une autre raison pourrait être que les options Deribit sont marginalisées et réglées en Bitcoin, même si leur valeur sous-jacente est la valeur USD de l’indice BTC. Pour obtenir le paiement d’expiration, la différence entre la valeur BTC en USD et le prix d’exercice de l’option (également coté en USD) est calculée et le résultat est converti en Bitcoin en utilisant la valeur de l’indice BTC à l’expiration. Remarque 8 La différence d’unités monétaires entre le prix de règlement (c’est-à-dire Bitcoin) et le sous-jacent (c’est-à-dire USD) est très similaire au gain d’une option FX quanto, sauf qu’il n’y a pas de contrats à terme ou d’options dans la direction opposée. Autrement dit, il n’existe pas de produits dérivés sur la valeur d’un dollar de Bitcoin, ni d’options utilisant la valeur d’un dollar de Bitcoin comme valeur sous-jacente. Pour cette raison, les options Bitcoin sont appelées « options inverses » et ne sont en fait qu’un des nombreux produits dérivés inverses, y compris les contrats à terme inverses, qui sont largement négociés sur de nombreuses bourses de produits dérivés de crypto-monnaie. Ils sont attractifs car les échanges de produits dérivés sur les croisements fiat-crypto peuvent être effectués sans utiliser de monnaie fiduciaire comme garantie sur un compte sur marge ou pour le règlement d’un contrat.

La question de savoir si Bitcoin peut exister en tant que marché monétaire au sens traditionnel du terme est un sujet de débat (Sauer, 2016), mais des marchés monétaires décentralisés très actifs pour Bitcoin (et d’autres devises et jetons) existent sur de nombreux sites de farming et différents pools de liquidité. Note 9 Nous pouvons donc convertir de l’USD en Bitcoin afin de mesurer l’effet de couverture de tout modèle en USD.

Quelle que soit la méthode de couverture que vous choisissez, la couverture elle-même est simple. Le trader ouvre une position sur une option et prend une position opposée sur l’actif sous-jacent avec une taille de position égale à la valeur Delta de l’option. Sur les marchés traditionnels, l’instrument de couverture est généralement un contrat à terme ayant la même échéance que l’option, car le prix de règlement n’est pas un instrument facilement négociable. Pour l’indice BTC, étant donné qu’il est basé sur une moyenne des prix du Bitcoin sur plusieurs bourses différentes, les mêmes commentaires s’appliquent. Mais cela ne signifie pas que l’instrument de couverture doit être un contrat à terme inverse avec la même échéance que l’option, car il existe des alternatives innovantes pour choisir des instruments de couverture négociables en Bitcoin. Premièrement, il existe trois types différents de contrats à terme à échéance finie : les contrats à terme linéaires standard, qui ne sont pas différents des contrats à terme sur les classes d’actifs traditionnelles ; les contrats à terme linéaires sur Bitcoin contre des pièces stables en USD (comme Tether), qui se négocient chaque fois que le prix du stablecoin s’écarte de son ancrage au dollar américain, qui introduit un risque de base ; et des contrats à terme inverses, qui ont des propriétés similaires aux contrats à terme linéaires en USD, mais sont marginés et réglés comme des crypto-monnaies. Note 10

Les options Bitcoin disposent également d’un outil de couverture qui utilise des contrats propres au marché des crypto-monnaies. Ces contrats sont souvent appelés contrats à terme perpétuels, swaps perpétuels ou simplement « contrats perpétuels », et constituent de loin le type de dérivés de crypto-monnaie le plus populaire. Leurs prix sont étroitement liés au prix spot, utilisant un mécanisme de « financement » qui paie ou reçoit automatiquement une petite partie de la position nette toutes les huit heures. Le calcul de ce pourcentage, appelé « taux de financement », varie d’une bourse à l’autre. Note 11 Le payeur et le destinataire dépendent du fait que le prix du contrat perpétuel est supérieur ou inférieur au prix au comptant (BTC). Lorsque le prix du contrat perpétuel est supérieur au prix spot, le taux de financement est positif et les utilisateurs détenant des positions longues sur des contrats perpétuels doivent payer des frais, tandis que les utilisateurs détenant des positions courtes reçoivent des frais. L’inverse est vrai lorsque le prix du contrat perpétuel est inférieur au prix spot. Les paiements de financement réguliers entre les positions longues et courtes maintiennent le prix du contrat perpétuel très proche du prix spot.

Sur Binance, la plus grande bourse de cryptomonnaies au comptant et de produits dérivés au monde, les deux tiers des produits de trading sont des contrats à terme perpétuels. Ce ratio entre le spot et les dérivés semble être la norme sur le marché des crypto-monnaies, comme le montre le rapport CryptoCompare (2022). Au moment où nous écrivons ces lignes, huit bourses de crypto-monnaies signalent des volumes quotidiens moyens de transactions à terme dépassant 1 milliard de dollars, la majorité de ce montant étant attribuable aux contrats perpétuels. Note 12 Ici, les échanges non réglementés tels que Binance, OKEx et Bybit représentent plus de 65 % de toutes les transactions à terme. En revanche, les bourses réglementées, notamment CME et FTX US, ont une part de marché beaucoup plus faible, d’environ 25 %. Les contrats à terme Deribit ont un volume de transactions quotidien moyen de plus de 4 milliards de dollars, ce qui lui fournit suffisamment de liquidités pour considérer ces contrats à terme comme des instruments de couverture appropriés. Cependant, comme pour d’autres bourses, la majorité des échanges se fait sur des contrats perpétuels plutôt que sur des contrats à terme calendaires. Pour illustrer cela, la figure 1 illustre les montants notionnels des transactions de ces contrats enregistrés quotidiennement mais lissés à l’aide d’une moyenne mobile sur 7 jours sur une période de deux ans commençant en janvier 2020. De toute évidence, les contrats à terme perpétuels ont un volume bien plus important que les contrats à terme à échéance déterminée, même si pour ces derniers nous avons agrégé les données de volume quotidiennes pour les trois types de contrats à terme, ainsi que les données pour chaque date d’expiration. En 2021, le volume des transactions sur contrats perpétuels a presque quadruplé par rapport à l’année précédente. Le tableau 1 démontre empiriquement cette évolution des volumes d’échanges. Il montre le volume quotidien moyen et l’intérêt ouvert pour trois principaux dérivés Bitcoin sur la bourse Deribit. Les volumes et l’intérêt ouvert sur tous les produits ont augmenté de manière significative entre 2020 et 2021, probablement en raison de l’intérêt pour l’espace crypto de la part des grandes banques et des sociétés de trading pour compte propre.

Figure 1. Volume quotidien moyen des transactions sur les contrats à terme et perpétuels de Deribit.

La figure 1 montre le volume quotidien moyen des contrats perpétuels (bleu) et le volume total moyen de tous les autres contrats à terme (rouge) de janvier 2020 à janvier 2022. Le volume quotidien est calculé en multipliant le nombre total de contrats négociés sur Deribit sur une période de 24 heures par leur valeur notionnelle de 10 $, puis en prenant la moyenne des sept derniers jours. Les résultats sont en milliards de dollars américains.

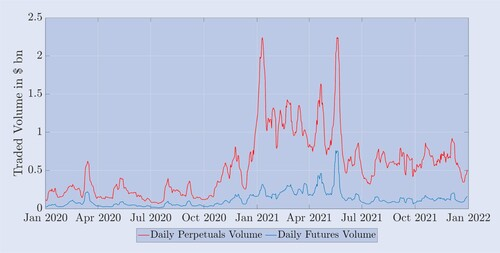
Tableau 1. Volume et intérêt ouvert des produits dérivés Bitcoin de Deribit.

3. Volatilité implicite du Bitcoin

La figure 2 illustre la dynamique empirique de la courbe de volatilité implicite dérivée des options Deribit, tracée sur une période de deux ans et demi dans une structure quotidienne. L’axe de la valeur monétaire représente la courbe de volatilité impliquée par le prix des options d’achat hors de la monnaie aux options de vente hors de la monnaie, où la valeur monétaire des options de vente hors de la monnaie est de 0,7, Le moneyness des options d’achat hors de la monnaie est de 1,3 et le moneyness des options à la monnaie est de 1,3. Les options d’achat et de vente ont toutes deux un moneyness de 1, et nous interpolons les données pour représenter ces niveaux de moneyness à une période d’expiration fixe de 30 jours. Plus de détails sur les données et leur filtrage sont donnés dans la section suivante.

Figure 2. Courbe de volatilité implicite du Bitcoin.

Courbe de volatilité implicite pour les options Bitcoin avec une période d’expiration constante de 30 jours, couvrant les données quotidiennes du 1er janvier 2020 au 30 juin 2022, dérivée d’options hors de la monnaie et à la monnaie. Les prix d’exercice varient de 30 % en dessous à 30 % au-dessus de la valeur actuelle de l’indice Bitcoin sous-jacent.

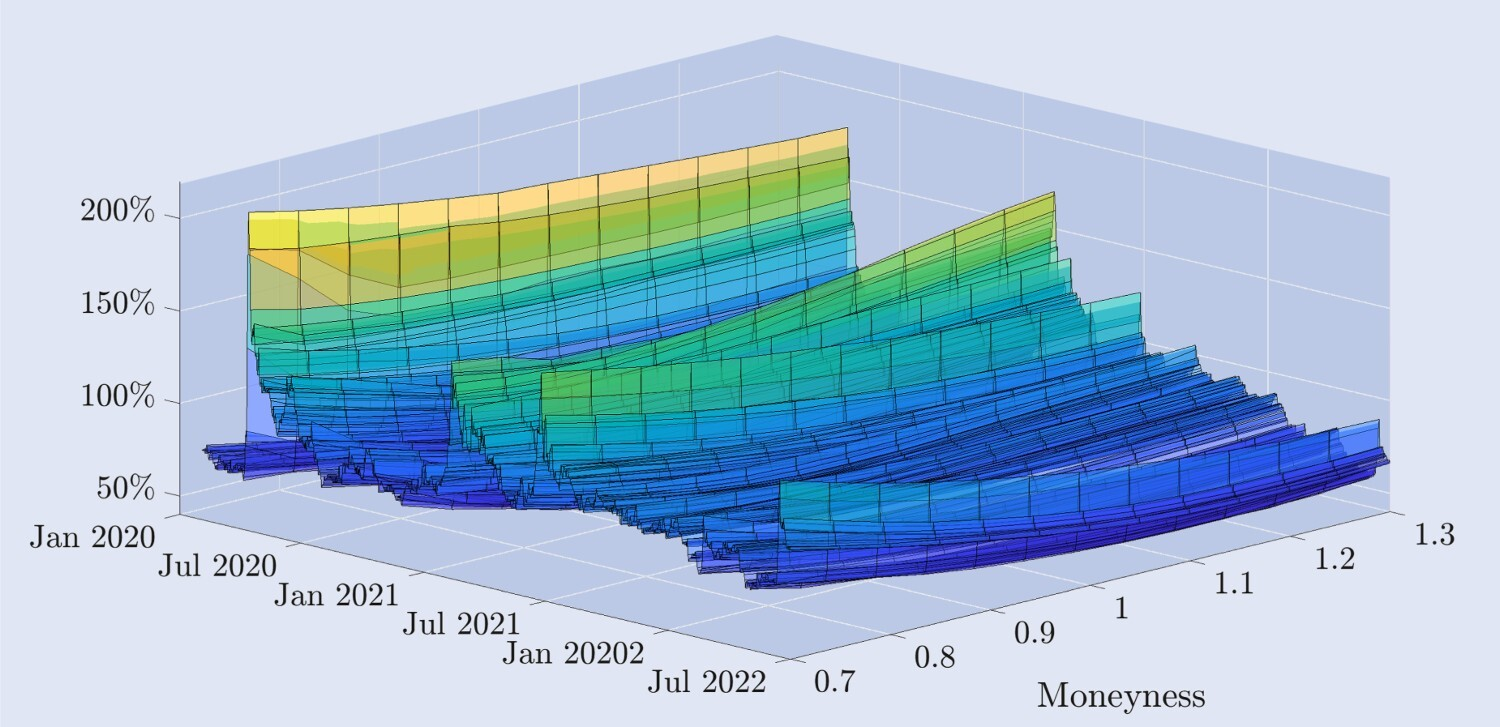
La forme de la courbe varie considérablement au fil du temps. Peu de temps après l’événement du « jeudi noir » de mars 2020, lorsque le prix du Bitcoin a chuté de plus de 30 % en quelques heures, la courbe de volatilité implicite a pris une forme négativement asymétrique, typique des options sur indices boursiers. C’est-à-dire, la volatilité des options de vente hors de la monnaie est beaucoup plus élevée que celle des options d’achat hors de la monnaie. Cependant, en général, les options Bitcoin ont une volatilité implicite beaucoup plus élevée que les options sur indices boursiers. Pendant la majeure partie de la période d’échantillonnage, la courbe de volatilité implicite présente une forme de « crosse de hockey », tandis que pendant les périodes particulièrement calmes, elle s’aplatit en un léger sourire symétrique. Il existe également des cas d’asymétrie positive, où la volatilité des options d’achat hors de la monnaie est bien supérieure à celle des options de vente hors de la monnaie. Ces caractéristiques ne sont pas courantes sur le marché des options sur indices boursiers, où le terme « skew » plutôt que « smile » est souvent utilisé pour les décrire. Pour étayer ce point, la figure 3 fournit une autre vision du sourire de volatilité implicite. Il montre la volatilité implicite du Bitcoin à différents niveaux de valeur monétaire (graphique du haut), ainsi que l’écart par rapport à la volatilité ATM, c’est-à-dire la différence entre la volatilité de la monnaie fixe et la volatilité ATM (graphique du bas). Dans la plupart des échantillons, les options de vente hors de la monnaie avec un moneyness de 0,7 ont la volatilité implicite la plus élevée. Sur les marchés boursiers traditionnels, ces options de vente très hors de la monnaie constituent une assurance intéressante contre la chute des cours des actions. Par exemple, dans le S&P 500, la forme prononcée et presque linéairement asymétrique de la courbe de volatilité implicite signifie que les options dont le prix augmente le plus après une baisse de l’actif sous-jacent sont celles qui ont la plus faible valeur monétaire. En revanche, la figure 3 montre qu’avant le krach du 12 mars 2020, la courbe de volatilité implicite du Bitcoin était relativement symétrique. Les options ATM ont la volatilité la plus faible, autour de 50 %, tandis que les options de vente et les options d’achat hors de la monnaie ont à peu près la même volatilité mais sont toutes deux plus élevées, la volatilité des options hors de la monnaie étant de 0,7 et 1,3 environ 75%. Cependant, il y a eu un sourire asymétrique évident dans le krach, avec des options de vente hors de la monnaie rapportant des primes plus élevées aux investisseurs peu enclins au risque au cas où les prix chuteraient à nouveau fortement. La volatilité implicite des options de vente à 30 jours, très hors de la monnaie, a soudainement grimpé à près de 200 %. Le Bitcoin a connu pour la première fois une nette tendance négative, mais la forme est toujours beaucoup plus plate par rapport aux formes asymétriques généralement observées dans les options sur indices boursiers. Cette asymétrie persiste, mais à mesure que le niveau de volatilité implicite diminue, la forme de la courbe de volatilité implicite commence à reprendre la forme d’un sourire.

Figure 3. Volatilité implicite du Bitcoin et biais ATM.

La figure montre la courbe de volatilité implicite pour les options Bitcoin avec une durée de 30 jours et une plage horaire du 1er janvier 2020 au 30 juin 2022. La courbe est calculée à l’aide d’options hors de la monnaie et à la monnaie, avec des prix d’exercice allant d’une baisse de 30 % à une augmentation de 30 % de la valeur actuelle de l’indice Bitcoin.

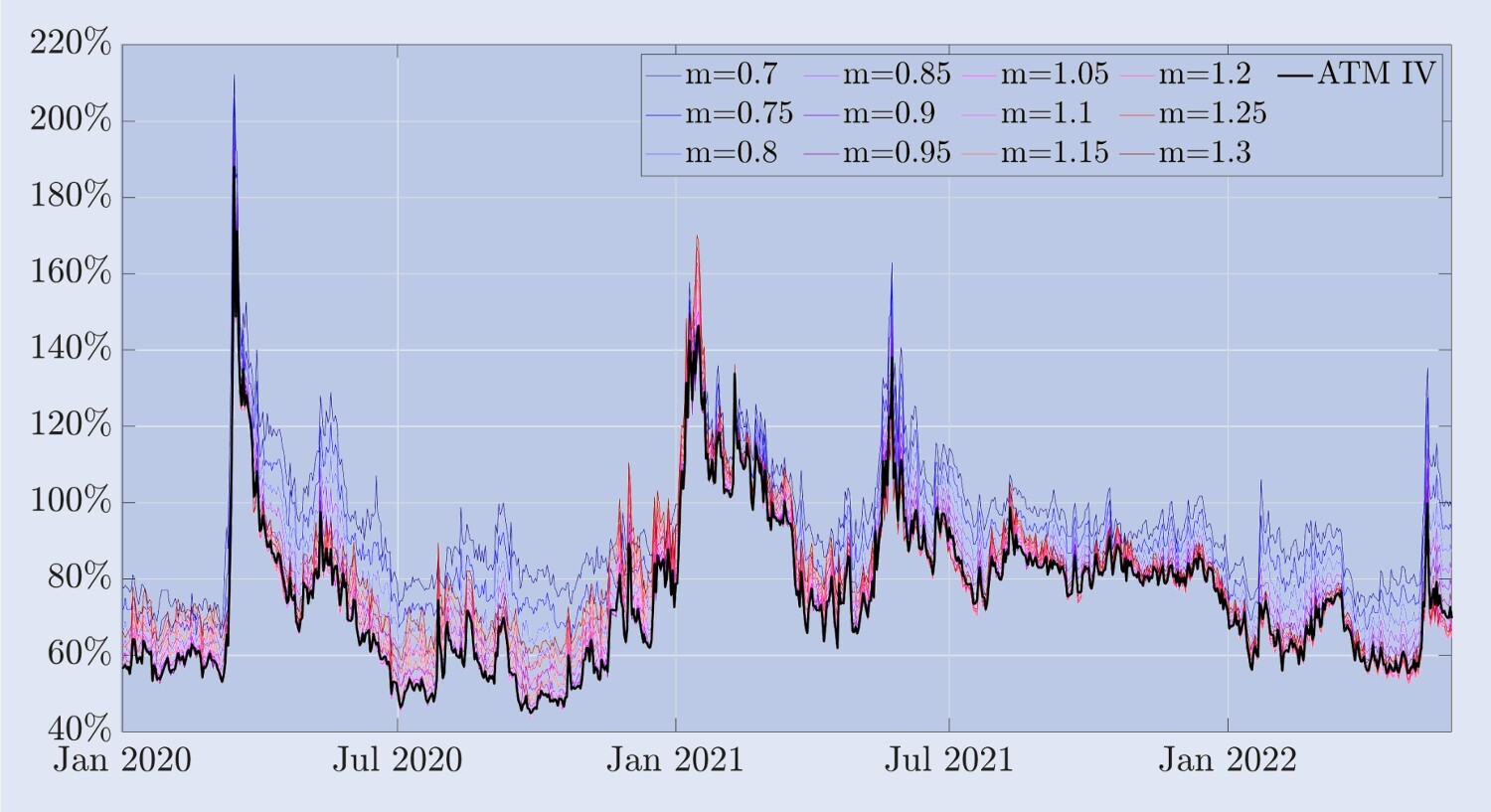
Sur la base de nos données d’échantillon, la volatilité implicite ATM (at the money) semble être le point le plus bas de la courbe du sourire et est négativement biaisée la plupart du temps. Cependant, contrairement aux options sur indices boursiers, la courbe souriante présente une asymétrie positive significative pendant les périodes de forte volatilité. Par exemple, lors du rallye du Bitcoin en juin 2021, la pente de la courbe du sourire a augmenté et est restée positivement biaisée pendant plusieurs mois. Alors que la corrélation entre les prix des indices boursiers et la volatilité est presque toujours importante et négative, la corrélation entre les prix du Bitcoin et sa volatilité implicite semble dépendre des conditions du marché. D’août 2019 à novembre 2020, la corrélation entre le prix du Bitcoin et la volatilité implicite ATM sur 30 jours était d’environ -0,42 ; au cours des cinq mois suivants, la corrélation est passée à 0,74 ; et en 2022, la corrélation est passée à 0,74. De juillet à novembre En 2017, la corrélation entre le prix et la volatilité était de 0,08.

Cependant, certaines caractéristiques sont similaires à celles de la volatilité implicite des options sur indices boursiers : (i) la volatilité des différentes virtualités est fortement corrélée à la volatilité à parité de la même échéance, comme le montre la figure 3 ; (ii) la volatilité implicite des options sur indices boursiers est fortement corrélée à la volatilité à parité de la même échéance, comme le montre la figure 3 ; La structure des termes de volatilité montre des fluctuations régulières entre les contrats à terme inversés à forte volatilité et les contrats à terme à terme relativement calmes. La figure 4 montre que, de manière similaire à la structure des termes de volatilité des indices boursiers, la volatilité implicite du Bitcoin présente des fluctuations plus faibles et des tendances similaires pendant la majeure partie de la période des contrats à terme inverses.

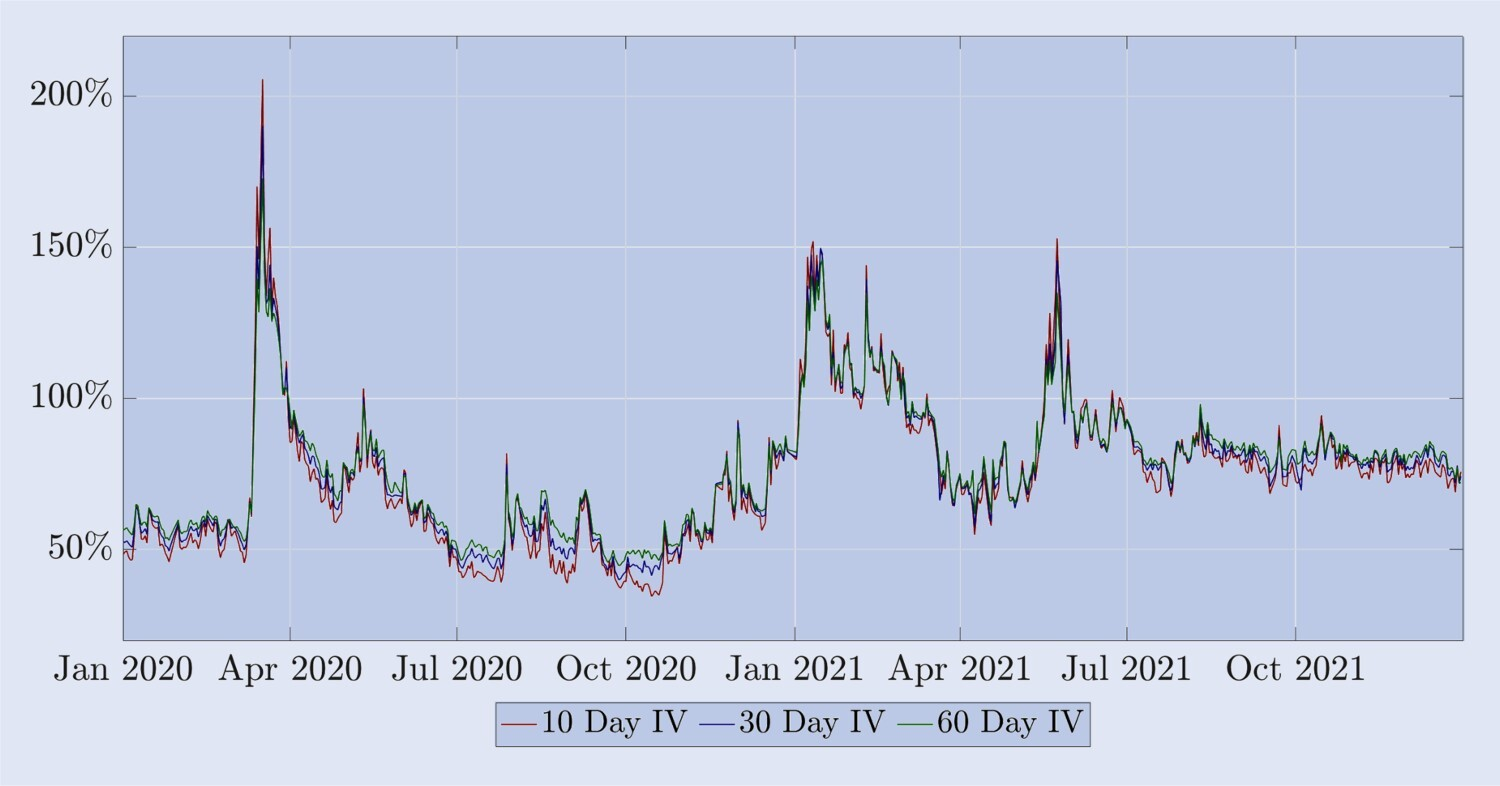
Figure 4. Structure des termes de volatilité implicite de Bitcoin.

La structure à terme de la volatilité implicite des options Bitcoin, y compris les dates d’expiration constantes de 10, 20 et 30 jours, du 1er janvier 2020 au 31 décembre 2021, calculée sur la base d’options à la monnaie. Durant les périodes relativement calmes, la structure par terme montre des futurs positifs, alors que durant les krachs (notamment en mars 2020 et juin 2021), c’est l’inverse qui se produit.

Nous commençons le reste de cet article en utilisant les caractéristiques des options et des contrats à terme Bitcoin que nous avons soulignées ci-dessus. Un détenteur de Bitcoin à long terme peut acheter une option de vente hors de la monnaie pour se protéger contre une baisse de prix significative et envisager de couvrir la position au comptant de manière appropriée. Cependant, les teneurs de marché et autres traders professionnels participent activement à la couverture delta dynamique, car la couverture du risque des options est essentielle pour eux en tant que fournisseurs de liquidités. Ils pourraient utiliser BS Delta pour réaliser cette couverture, mais étant donné la prévalence de l’ajustement Smile Curve Delta parmi les traders d’options sur actions, il serait intéressant d’examiner l’efficacité de ce Delta pour les options Bitcoin. Nous avons examiné la littérature qui traite de l’efficacité du delta ajusté par la courbe souriante pour la couverture des options sur indices boursiers et avons montré que dans de nombreux cas, le delta BS est aussi efficace que n’importe quel delta ajusté par la courbe souriante. Cependant, aucune recherche antérieure n’a exploré cette question pour les options Bitcoin, et il est clair - d’après le comportement très différent de la courbe de volatilité implicite Bitcoin que nous venons de discuter et l’éventail de nouveaux instruments de couverture disponibles pour Bitcoin - que nous ne pouvons pas simplement extrapoler ce que l’on sait des options sur indices boursiers pour tirer des conclusions sur les options de couverture Bitcoin. Par conséquent, le but de cette étude est d’introduire et de comparer différents deltas ajustés de la courbe souriante couramment utilisés par les praticiens pour analyser leur efficacité à minimiser l’écart type des erreurs de couverture des options Bitcoin en fonction de différents choix d’instruments de couverture. En fait, ces recherches pourraient même être étendues au niveau des bourses où ont lieu les transactions d’options et/ou de couverture. Par exemple, est-il préférable d’utiliser les contrats à terme ou perpétuels de Binance ou de Deribit pour couvrir les options cotées sur la bourse Deribit ? Mais nous ne discutons pas de ce niveau détaillé du problème de couverture des options Bitcoin dans cette étude. Au moins actuellement, au moment de la rédaction de cet article, le marché des options Deribit représente plus de 90 % de tout le volume des options Bitcoin, et les communications personnelles avec les teneurs de marché des options Deribit indiquent qu’ils n’utilisent la plateforme à terme Deribit que pour les activités de couverture delta.

4. Ratio de couverture

Dans notre conception expérimentale, nous écrivons une option européenne standard sur des contrats à terme sur indice Bitcoin d’une valeur d’un Bitcoin et la couvrons en prenant une position longue sur un certain nombre de contrats à terme. Les contrats à terme expirant en T permettent aux traders de conclure un accord pour acheter ou vendre une certaine quantité de Bitcoin à un moment futur T à un taux de change Bitcoin-USD désormais convenu. L’actif sous-jacent des contrats à terme et des options est le Deribit Bitcoin Index BTC, qui est un indice composite non négociable. Cependant, nous pouvons également couvrir les options d’expiration T avec une position de contrat perpétuel au lieu d’un contrat à terme d’expiration T. Nous pouvons omettre le temps d’exécution t dans notre notation sans provoquer de confusion, et nous désignons le prix à l’instant t d’une option inverse avec un prix d’exercice K et une date d’expiration T comme f(K,T|F,σ), où F est Le prix perpétuel ou prix à terme expirant à T, à l’instant t, σ:=σt(K,T|F) représente la volatilité implicite de l’option, qui est également la volatilité à l’instant t. En intégrant la relation entre la volatilité et l’actif sous-jacent dans notre cadre de couverture, nous visons à obtenir un delta plus précis que le delta BS, à savoir le delta δadj ajusté par le sourire basé sur la règle de la chaîne.

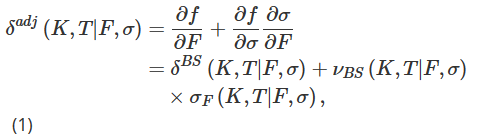
Où δBS est le delta BS standard, νBS est la sensibilité à la volatilité du prix de l’option BS (vega), et σF = ∂σ/∂F est la sensibilité à la volatilité au prix, c’est-à-dire la variation de la volatilité implicite aux variations de l’actif sous-jacent . . Bien que BS delta et vega aient des formules fermées et soient faciles à calculer, la quantification de σF est relativement difficile et il existe de nombreuses méthodes différentes.

Le premier ajustement du delta BS dont nous avons discuté trouve ses racines dans différentes manières de paramétrer la volatilité locale différemment selon l’état actuel du marché ou le « régime du marché ». Le concept de volatilité locale a été développé dans un large éventail de littérature académique, à commencer par les articles classiques de Dupire (1994) et Derman et al. (1996). Le « modèle collant », préconisé par Derman (1999) dans le contexte de la couverture des options sur indices boursiers, qui applique différentes paramétrisations de volatilité locale aux nœuds d’un arbre binaire modélisant l’évolution du prix de l’actif sous-jacent, présente ici un intérêt particulier. Derman et al. (1996) ont proposé d’approcher σF comme la pente de la volatilité implicite par rapport au prix d’exercice : Note 13

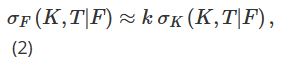
Parmi eux, σK=∂σ/∂K représente la dérivée de la volatilité par rapport au prix d’exercice, et k devrait dépendre du mécanisme actuel du marché. En fait, Derman (1999) a introduit trois « modèles de rigidité » différents pour représenter le comportement de la volatilité locale sous différents régimes de marché. Le modèle Sticky Strike (SS) décrit une situation de marché en tendance et suppose que la volatilité est indépendante des mouvements de prix futurs de l’actif sous-jacent et, comme l’hypothèse BS, est constante et la même pour chaque option. Dans ce mécanisme, delta est égal au delta BS. Note 14 Le modèle Sticky Money (SM) (parfois également appelé Sticky Delta) considère un marché limité par une fourchette. Dans ce mécanisme, la volatilité d’une option dépend uniquement de sa valeur monétaire (ou de manière équivalente de son delta). Par conséquent, la volatilité locale est la même à chaque nœud de l’arbre, mais chaque option a un arbre différent avec une volatilité locale différente, en fonction de la valeur monétaire de l’option. À mesure que le prix de l’actif sous-jacent change, la valeur monétaire de l’option change et nous devons passer à un arbre différent pour évaluer l’option. Enfin, le modèle Sticky Tree (ST) capture le comportement de la volatilité locale lors des baisses rapides du marché, c’est-à-dire qu’il décrit un ajustement de la courbe souriante lorsqu’il existe une forte corrélation négative entre la volatilité et le prix de l’actif sous-jacent. Le nom de ce modèle d’arbre caché vient du modèle de volatilité locale proposé par Derman et Kani (1994). De même, la volatilité locale est une fonction déterministe, mais elle peut être différente à chaque nœud de l’arbre, et le même arbre est utilisé pour évaluer toutes les options. Dans ces trois types différents de paramétrisation de la volatilité locale, la valeur de k dans la formule (2) sera différente selon le mécanisme du marché, comme indiqué ci-dessous :

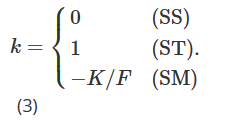
Crépey (2004) et Alexander et al. (2012) ont tous deux étendu l’approximation (2) pour inclure la dépendance de l’état de k. Notons également qu’en combinant les équations (1) et (2) d’Alexander et al. (2012) avec l’équation (3) d’Alexander et Nogueira (2007b) et en effectuant quelques manipulations algébriques, on peut constater que la courbe du sourire de Bates ( 2005) est implicitement Le delta invariant d’échelle (généralisé dans Alexander et Nogueira (2007a)) est identique à l’approximation de l’argent collant (SM).

Compte tenu de la forte volatilité du Bitcoin, la gamme des prix d’exercice disponibles peut varier considérablement au fil du temps. Par conséquent, pour fournir un cadre permettant d’étudier les options présentant les mêmes caractéristiques sur une période plus longue, nous passons des prix d’exercice aux indicateurs in-the-money. Nous définissons la monétisation m comme m=K/F, et utilisons maintenant θ(m,T|F)=σ(mK,T|F) pour représenter la volatilité implicite. En désignant les dérivées partielles de θ(m,T|F) par rapport à F et m comme θF(m,T|F) et θm(m,T|F) respectivement, nous pouvons réécrire le delta ajusté (7) comme :

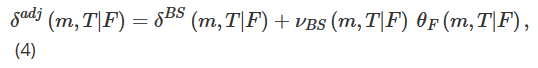
Nous utilisons l’hypothèse de volatilité locale proposée par Derman (1999) pour estimer la sensibilité volatilité-prix θF. La structure arborescente utilisée pour simuler l’évolution du prix des options différera en fonction des trois modèles de marché possibles : Stable Trend Market (SS), Range Market (SM) et Jump Crash Market (ST). Par conséquent, en convertissant le delta collant de Derman (1999) en une mesure monétaire, la valeur de κ dans (5) devrait être différente selon le modèle de marché.

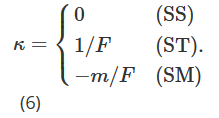
Comme précédemment, le Delta sans modèle, implicite au sourire et invariant à l’échelle proposé par Bates (2005) et Alexander et Nogueira (2007a) est identique au Delta de mesure de l’argent collant (SM) de Derman et Kani (1994).

Ensuite, nous considérons la variance minimale (VM) Delta δmv, c’est-à-dire le Delta qui minimise la variance instantanée du portefeuille de couverture Delta. Nous suivons ici une approximation introduite par Bakshi et al. (1997) qui minimise la variance locale. Lee (2001) montre que cet ajustement du ratio de couverture MV est de la même ampleur que le delta implicite Smile (SM), mais de signe opposé, c’est-à-dire :

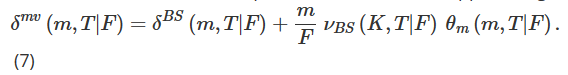
Comme expliqué en détail dans le chapitre 4 d’Alexander (2008), et également dans d’autres textes sur la volatilité implicite, le delta implicite du sourire crée une dynamique de « sourire flottant » contre-intuitive qui signifie également que lorsque la volatilité Lorsque la corrélation taux-prix est importante et négatif (c’est-à-dire qu’il existe une asymétrie négative significative), la performance de couverture produite par l’ajustement SM est nettement pire que celle du BS Delta. Étant donné que l’ajustement MV a un signe opposé à l’ajustement SM, le delta MV doit être préféré au delta BS lors de la couverture des options sur indices boursiers et de toute option avec une courbe de volatilité implicite présentant une pente négative significative.

Notre ajustement final de la courbe du sourire Delta, noté δhw, est proposé par Hull et White (2017). Il est dérivé de l’estimation empirique de la relation quadratique entre la valeur absolue du PnL ΔP quotidien du portefeuille de couverture BS Delta et le BS Delta. C’est-à-dire:

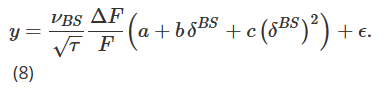
où ΔF est le PnL quotidien des contrats à terme. Après avoir obtenu des estimations de paramètres (aˆ, bˆ, cˆ) à l’aide de données historiques, le delta de Hull et White (HW) est calculé comme suit :

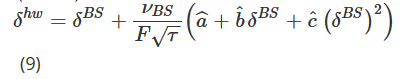
où δBS et νBS représentent le BS classique Delta et vega. Le prix sous-jacent actuel est noté F, sa variation est notée ΔF et τ représente l’heure d’expiration de l’option. Les auteurs calculent les estimations (aˆ, bˆ, cˆ) en utilisant une fenêtre glissante de 36 mois, puis analysent la performance de la couverture HW Delta pour minimiser l’écart type de l’erreur de couverture quotidienne pour une période de 11 ans commençant en janvier 2014. S&P 500 et autres options sur indices boursiers. Ils ont découvert que l’utilisation de HW Delta pouvait améliorer les performances jusqu’à 26 %. D’autres conclusions sont basées uniquement sur les options sur indices boursiers et soutiennent que HW Delta surpasse les options de vente pour les appels et surpasse les options dans la monnaie pour les options hors de la monnaie. En outre, ils affirment que le HW Delta surpasse de nombreux autres deltas dérivés de divers modèles de volatilité stochastique et de volatilité locale lors de la couverture des options sur indices boursiers.

Cette section couvre une série d’ajustements simples du BS Delta qui ont prouvé leur efficacité dans des recherches antérieures sur la couverture des options sur indices boursiers et d’autres classes d’actifs traditionnelles. La question est maintenant de savoir s’ils peuvent également surpasser la simple couverture BS Delta sur le marché des options Bitcoin. Le marché des options Bitcoin est moins mature que les marchés d’options traditionnels, et sa volatilité et sa pression d’achat directionnelle sont plus importantes, et les teneurs de marché rééquilibrent leurs inventaires en fonction des informations provenant de ces pressions. Nous résumons les ratios de couverture delta ajustés BS considérés dans cette étude dans la formule unique suivante :

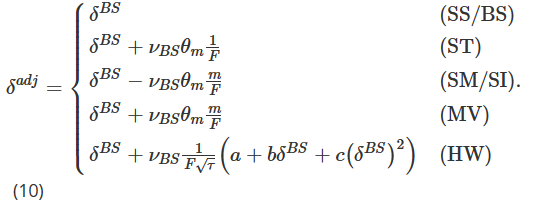
Nous expliquons le contenu ci-dessus comme suit :

1. Lorsque m=1, c’est-à-dire dans une option à la monnaie, l’ajustement MV est le même que l’ajustement ST ; sinon, lorsque m>1, c’est-à-dire dans une option d’achat hors de la monnaie, la taille de l’ajustement MV est supérieure à l’ajustement ST ; lorsque m, c’est-à-dire, dans une option de vente hors de la monnaie, la taille de l’ajustement MV est inférieure à l’ajustement ST ;

2. L’ajustement MV est toujours de taille égale et de direction opposée à l’ajustement SM, et le delta SM est également le delta invariant d’échelle (SI) sans modèle d’Alexander et Nogueira (2007a), c’est-à-dire le delta de tout type de processus de saut de volatilité stochastique dans les prix des options Bitcoin ;

3. Les signes des ajustements ST, SM et MV dépendent de la pente de la courbe de volatilité implicite, θm. Lorsque la pente est négative, les deltas MV et ST sont inférieurs au delta BS/SS, tandis que le delta SM/SI est supérieur au delta BS/SS. Lorsque la pente est positive, MV et ST Delta sont supérieurs à BS/SS Delta, tandis que SM/SI Delta est inférieur à BS/SS Delta.

5. Données

Nous avons créé une base de données unique en prenant des instantanés horaires des données du marché des options Deribit sur une période de plusieurs années à l’aide de l’API d’échange. Ces données contiennent les informations du carnet d’ordres de niveau 1 pour toutes les options, contrats à terme et contrats perpétuels. Dans cet article, nous utilisons uniquement des données avec des fréquences de huit heures et quotidiennes, couvrant une période de deux ans du 1er janvier 2020 au 1er janvier 2022.

La figure 5 représente le prix de règlement quotidien de l’indice BTC (c’est-à-dire le prix à 00h00 UTC) et le volume total de toutes les options et contrats perpétuels négociés sur Deribit au cours des dernières 24 heures (en montants notionnels, en milliards de USD). . Les contrats à terme ne sont pas inclus ici car leurs volumes de négociation sont bien inférieurs à ceux des contrats perpétuels et des options, comme le montre la figure 1. Au cours de l’année 2020, l’indice BTC a augmenté relativement lentement, passant de niveaux autour de 7 000 \( jusqu'à la première grande période haussière qui a débuté en novembre 2020, la valeur de l'indice atteignant près de 28 000 \) à la fin de 2020. En 2021, l’indice BTC a doublé de janvier (environ 28 000 \() à mi-avril 2021 (environ 59 000 \)), puis a chuté de près de 50 % jusqu’à retomber à 30 000 \( à la mi-juillet. Il a atteint un sommet historique d'environ 69 000 \) le 8 novembre 2021. Le panneau central de la figure 5 montre qu’au cours de l’année 2020, le volume total des transactions sur 24 heures de toutes les options sur Deribit était relativement faible, dépassant à peine 500 millions de dollars. Cependant, en 2021, les marchés ont été clairement volatils ou en tendance, avec des volumes d’options quotidiens atteignant 3 milliards de dollars en moyenne. Le nombre de contrats d’options différents négociés a également presque doublé, passant de 4,3 millions en janvier 2021 à 6,2 millions à la fin de l’année. Le graphique ci-dessous montre le volume quotidien des transactions des contrats perpétuels, qui ont connu une activité commerciale plus élevée en 2021, en particulier au premier semestre de l’année. Il est intéressant de noter que la croissance des échanges de contrats perpétuels a été plus faible que celle des options au cours du second semestre 2021. Ce dernier est probablement dû à l’introduction d’un certain nombre de nouveaux contrats fin 2020 et début 2021, que les traders ont progressivement adoptés pour la couverture gamma et vega. Cela a peut-être allégé la pression sur la couverture delta dynamique extrêmement active au cours du second semestre 2021. En fait, comme le montre la figure 1, les volumes de transactions pour les contrats à terme ont également diminué au cours des six derniers mois de 2021, encore plus que pour les contrats perpétuels. Quoi qu’il en soit, le constat que les tendances commerciales en 2020 et 2021 étaient si différentes nou