Un outil puissant pour les traders programmatiques: algorithme de mise à jour progressive pour calculer la moyenne et la variance

Introduction au projet

Dans le trading programmatique, il est souvent nécessaire de calculer des moyennes et des variances, comme le calcul des moyennes mobiles et des indicateurs de volatilité. Lorsque nous avons besoin de calculs à haute fréquence et à long terme, il est nécessaire de conserver les données historiques pendant une longue période, ce qui est à la fois inutile et consommateur de ressources. Cet article présente un algorithme de mise à jour en ligne pour le calcul des moyennes pondérées et des variances, ce qui est particulièrement important pour le traitement des flux de données en temps réel et l'ajustement dynamique des stratégies de trading, en particulier les stratégies à haute fréquence.

Moyenne simple et variance

Si nous utilisons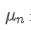pour représenter la valeur moyenne du nème point de données, en supposant que nous ayons déjà calculé la moyenne de n-1 points de données /upload/asset/28e28ae0beba5e8a810a6.png, nous recevons maintenant un nouveau point de données /upload/asset/28d4723cf4cab1cf78f50.png. Nous voulons calculer le nouveau nombre moyen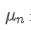La déduction suivante est détaillée.

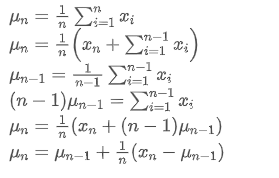
Le processus de mise à jour de la variance peut être décomposé en les étapes suivantes:

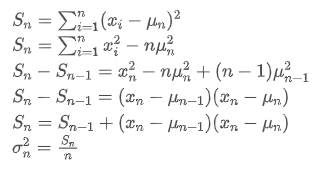
Comme on peut le voir dans les deux formules ci-dessus, ce processus nous permet de mettre à jour de nouvelles moyennes et variances à chaque nouvelle donnée.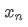Le problème est que ce que nous calculons de cette façon est la moyenne et la variance de tous les échantillons, alors que dans les stratégies réelles, nous devons considérer une certaine période fixe. L'observation de la mise à jour moyenne ci-dessus montre que la quantité de nouvelles mises à jour moyennes est un écart entre les nouvelles données et les moyennes passées multiplié par un ratio. Si ce ratio est fixe, cela conduira à une moyenne pondérée exponentiellement, dont nous parlerons ensuite.

Moyenne pondérée exponentiellement

La moyenne pondérée exponentielle peut être définie par la relation récursive suivante:

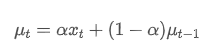
Parmi eux,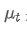est la moyenne pondérée exponentielle au moment t,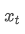est la valeur observée au moment t, α est le facteur de poids, et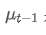est la moyenne pondérée exponentielle du point de temps précédent.

Variance pondérée exponentiellement

En ce qui concerne la variance, nous devons calculer la moyenne pondérée exponentielle des écarts carrés à chaque point de temps.

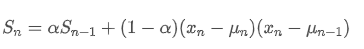
Parmi eux,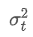est la variance pondérée exponentielle au moment t, et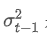est la variance pondérée exponentielle du point de temps précédent.

Observez la moyenne pondérée exponentiellement et la variance, leurs mises à jour incrémentielles sont intuitives, en conservant une partie des valeurs passées et en ajoutant de nouveaux changements.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA et EMA

La SMA (également connue sous le nom de moyenne arithmétique) et l'EMA sont deux mesures statistiques courantes, chacune ayant des caractéristiques et des utilisations différentes. La première attribue un poids égal à chaque observation, reflétant la position centrale de l'ensemble de données. La seconde est une méthode de calcul récursive qui donne un poids plus élevé aux observations plus récentes. Les poids diminuent de manière exponentielle à mesure que la distance du temps actuel augmente pour chaque observation.

• Répartition du poids: La SMA attribue la même pondération à chaque point de données, tandis que l'EMA accorde une plus grande pondération aux points de données les plus récents.
• Sensibilité aux nouvelles informations: l'AEM n'est pas suffisamment sensible aux données nouvellement ajoutées, car il s'agit de recalculer tous les points de données.
• Complicité de calcul: Le calcul de la SMA est relativement simple, mais à mesure que le nombre de points de données augmente, le coût de calcul augmente également.

Méthode de conversion approximative entre la EMA et la SMA

Bien que SMA et EMA soient conceptuellement différentes, nous pouvons faire de l'EMA une approximation d'une SMA contenant un nombre spécifique d'observations en choisissant une valeur α appropriée.

Le SMA est la moyenne arithmétique de tous les prix dans une fenêtre de temps donnée. Pour une fenêtre de temps N, le centroid du SMA (c'est-à-dire la position où se trouve le nombre moyen) peut être considéré comme:

le centroid de la SMA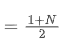

L'EMA est un type de moyenne pondérée où les points de données les plus récents ont un poids plus important.

le centroid de l'EMA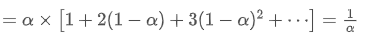

Lorsque nous supposons que SMA et EMA ont le même centroid, nous pouvons obtenir:

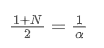
Pour résoudre cette équation, nous pouvons obtenir la relation entre α et N.

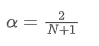
Cela signifie que pour une SMA donnée de N jours, la valeur α correspondante peut être utilisée pour calculer une EMA équivalente, de sorte qu'ils aient le même centroid et que les résultats soient très similaires.

Conversion de l'EMA avec des fréquences de mise à jour différentes

Supposons que nous ayons une EMA qui se met à jour toutes les secondes, avec un facteur de poids de /upload/asset/28da19ef219cae323a32f.png. Cela signifie que chaque seconde, le nouveau point de données sera ajouté à l'EMA avec un poids de /upload/asset/28da19ef219cae323a32f.png, tandis que l'influence des anciens points de données sera multipliée par /upload/asset/28cfb008ac438a12e1127.png.

Si nous changeons la fréquence de mise à jour, comme la mise à jour une fois toutes les f secondes, nous voulons trouver un nouveau facteur de poids /upload/asset/28d2d28762e349a03c531.png, de sorte que l'impact global des points de données dans f secondes est le même que lors de la mise à jour chaque seconde.

Dans un délai de f secondes, si aucune mise à jour n'est effectuée, l'impact des anciens points de données diminuera continuellement de f fois, chaque fois multiplié par /upload/asset/28e50eb9c37d5626d6691.png. Par conséquent, le facteur de déclin total après f secondes est /upload/asset/28e296f97d8c8344a2ee6.png.

Afin que l'EMA mise à jour toutes les f secondes ait le même effet de désintégration que l'EMA mise à jour toutes les secondes au cours d'une période de mise à jour, nous définissons le facteur de désintégration total après f secondes égal au facteur de désintégration au cours d'une période de mise à jour:

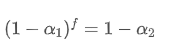
En résolvant cette équation, nous obtenons de nouveaux facteurs de poids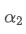

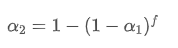
Cette formule fournit la valeur approximative du nouveau facteur de poids /upload/asset/28d2d28762e349a03c531.png, qui maintient l'effet de lissage EMA inchangé lorsque la fréquence de mise à jour change.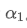avec une valeur de 0,001 et la mettre à jour toutes les 10 secondes, si elle est modifiée à une mise à jour toutes les secondes, la valeur équivalente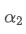serait d'environ 0,01.

Mise en œuvre du code Python

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Résumé

Dans le trading programmatique à haute fréquence, le traitement rapide des données en temps réel est crucial. Pour améliorer l'efficacité de calcul et réduire la consommation de ressources, cet article présente un algorithme de mise à jour en ligne pour calculer en continu la moyenne pondérée et la variance d'un flux de données. Les mises à jour incrémentielles en temps réel peuvent également être utilisées pour divers calculs de données statistiques et d'indicateurs, tels que la corrélation entre les prix de deux actifs, l'ajustement linéaire, etc., avec un grand potentiel.