Le trading par paire basé sur une technologie basée sur les données

Le trading par paire basé sur une technologie basée sur les données

Le trading par paire est un bon exemple de la formulation de stratégies de trading basées sur l'analyse mathématique.

Principes de base

Supposons que vous ayez une paire d'objectifs d'investissement X et Y qui ont des connexions potentielles. Par exemple, deux entreprises produisent les mêmes produits, tels que Pepsi Cola et Coca Cola. Vous voulez que le rapport de prix ou les spreads de base (également appelés différence de prix) des deux restent inchangés au fil du temps. Cependant, en raison des changements temporaires de l'offre et de la demande, tels qu'un grand ordre d'achat / vente d'une cible d'investissement et la réaction à l'une des nouvelles importantes de l'une des entreprises, la différence de prix entre les deux paires peut être différente de temps en temps. Dans ce cas, un objet d'investissement augmente tandis que l'autre diminue par rapport à l'autre. Si vous voulez que ce désaccord revienne à la normale au fil du temps, vous pouvez trouver des opportunités de trading (ou des opportunités d'arbitrage).

Lorsqu'il y a une différence de prix temporaire, vous vendez l'objet d'investissement avec une excellente performance (l'objet d'investissement en hausse) et achetez l'objet d'investissement avec une mauvaise performance (l'objet d'investissement en baisse). Vous êtes sûr que la marge d'intérêt entre les deux objets d'investissement finira par chuter en raison de la chute de l'objet d'investissement avec une excellente performance ou de la hausse de l'objet d'investissement avec une mauvaise performance, ou les deux. Votre transaction fera de l'argent dans toutes ces situations similaires. Si les objets d'investissement augmentent ou diminuent ensemble sans changer la différence de prix entre eux, vous ne gagnerez ni ne perdrez d'argent.

Par conséquent, la négociation par paire est une stratégie de négociation neutre sur le marché, qui permet aux opérateurs de tirer profit de presque toutes les conditions du marché: tendance haussière, tendance baissière ou consolidation horizontale.

Expliquer le concept: deux objectifs hypothétiques d'investissement

• Construire notre environnement de recherche sur la plateforme FMZ Quant

Tout d'abord, afin de travailler en douceur, nous devons construire notre environnement de recherche.FMZ.COM) pour construire notre environnement de recherche, principalement pour utiliser l'interface API pratique et rapide et le système Docker bien emballé de cette plateforme plus tard.

Dans le nom officiel de la plateforme FMZ Quant, ce système Docker est appelé le système Docker.

Veuillez consulter mon précédent article sur le déploiement d'un docker et d'un robot:https://www.fmz.com/bbs-topic/9864.

Les lecteurs qui veulent acheter leur propre serveur de cloud computing pour déployer des dockers peuvent se référer à cet article:https://www.fmz.com/digest-topic/5711.

Après avoir déployé avec succès le serveur de cloud computing et le système docker, nous allons ensuite installer le plus grand artefact actuel de Python: Anaconda.

Afin de réaliser tous les environnements de programme pertinents (bibliothèques de dépendances, gestion de version, etc.) requis dans cet article, le moyen le plus simple est d'utiliser Anaconda.

Pour la méthode d'installation d'Anaconda, veuillez consulter le guide officiel d'Anaconda:https://www.anaconda.com/distribution/.

Cet article utilisera également numpy et pandas, deux bibliothèques populaires et importantes dans l'informatique scientifique Python.

Le travail de base ci-dessus peut également faire référence à mes articles précédents, qui présentent comment configurer l'environnement Anaconda et les bibliothèques numpy et pandas. Pour plus de détails, veuillez vous référer à:https://www.fmz.com/bbs-topic/9863.

Ensuite, utilisons le code pour mettre en œuvre un deux objectifs hypothétiques d'investissement:

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Oui, nous allons aussi utiliser matplotlib, une très célèbre bibliothèque de graphiques en Python.

Générons une cible hypothétique d'investissement X, et simulons et traçons son rendement quotidien à travers la distribution normale.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

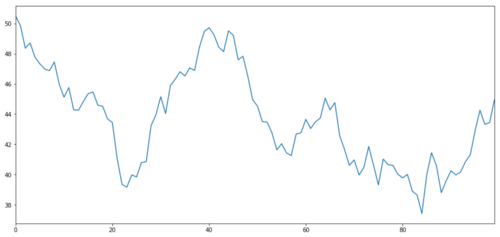
Le X de l'objet d'investissement est simulé pour tracer son rendement quotidien par une distribution normale

Maintenant, nous générons Y, qui est fortement intégré avec X, donc le prix de Y devrait être très similaire à la modification de X. Nous modélisons ceci en prenant X, le déplacer vers le haut et en ajoutant un bruit aléatoire extrait de la distribution normale.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

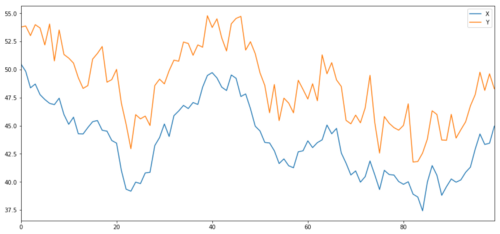
X et Y de l'objet d'investissement de cointégration

Cointégration

La cointégration est très similaire à la corrélation, ce qui signifie que le rapport entre deux séries de données changera près de la valeur moyenne.

Y = X + e

où est un rapport constant et e est le bruit.

Pour les paires qui négocient entre deux séries temporelles, la valeur attendue du ratio au fil du temps doit converger à la valeur moyenne, c'est-à-dire qu'elles doivent être cointégrées.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

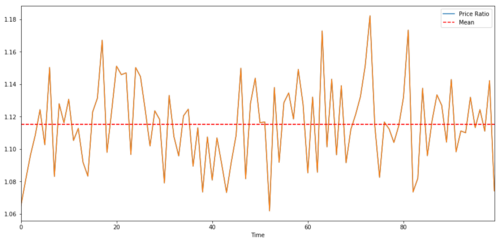
Rapport et valeur moyenne entre deux prix cibles d'investissement cointégrés

Essai de cointégration

Une méthode de test pratique est d'utiliser statsmodels.tsa.stattools. Nous verrons une très faible valeur p, parce que nous avons créé deux séries de données artificiellement qui sont aussi co-intégrées que possible.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Le résultat est: 1.81864477307e-17

Note: corrélation et cointégration

La corrélation et la cointégration, bien que similaires en théorie, ne sont pas la même chose. Regardons des exemples de séries de données pertinentes mais non cointégrées et vice versa.

X.corr(Y)

Le résultat est: 0,951.

Comme nous nous y attendions, c'est très élevé. Mais qu'en est-il de deux séries liées mais non co-intégrées?

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

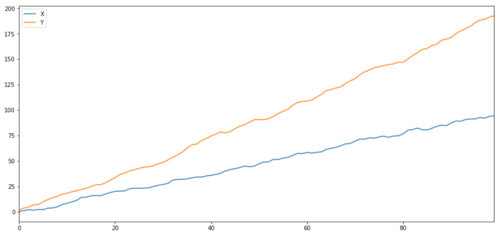
Deux séries apparentées (non intégrées)

Coefficient de corrélation: 0,998 Valeur P de l'essai de cointégration: 0,258

Des exemples simples de cointégration sans corrélation sont les séquences de distribution normale et les ondes carrées.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

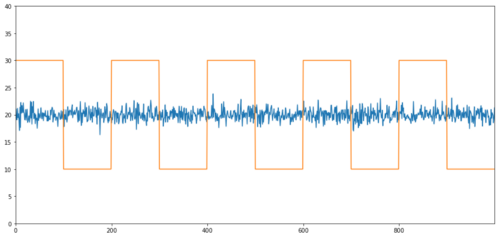
Corrélation: 0,007546 Valeur P du test de cointégration: 0,0

La corrélation est très faible, mais la valeur p montre une parfaite co-intégration!

Comment effectuer le trading de paires?

Parce que deux séries temporelles co-intégrées (comme X et Y ci-dessus) sont face à face et s'écartent l'une de l'autre, parfois les spreads de base sont élevés ou bas. Nous effectuons des transactions en paire en achetant un objet d'investissement et en vendant un autre. De cette façon, si les deux objectifs d'investissement tombent ou augmentent ensemble, nous ne gagnerons ni ne perdrons d'argent, c'est-à-dire que nous sommes neutres sur le marché.

Retour à ce qui précède, X et Y dans Y = X + e, de sorte que le rapport (Y / X) se déplace autour de sa valeur moyenne . Nous gagnons de l'argent grâce au rapport de la réversion de la valeur moyenne. Pour ce faire, nous allons prêter attention au cas où X et Y sont éloignés, c'est-à-dire que la valeur de est trop élevée ou trop faible:

• Dans l'exemple ci-dessus, nous ouvrons la position en allant long Y et en allant court X.

• Ratio de raccourcissement: C'est lorsque le ratio est très grand et que nous nous attendons à ce qu'il diminue. Dans l'exemple ci-dessus, nous ouvrons la position en raccourcissant Y et en allant long X.

S'il vous plaît noter que nous avons toujours une position de couverture: si le sujet de la négociation achète la valeur de perte, la position courte fera de l'argent, et vice versa, donc nous sommes immunisés à la tendance globale du marché.

Si le X et le Y de l'objet de négociation se déplacent par rapport l'un à l'autre, nous gagnerons de l'argent ou perdrons de l'argent.

Utilisez les données pour trouver des objets de trading avec un comportement similaire

La meilleure façon de le faire est de commencer par le sujet de négociation que vous soupçonnez être la co-intégration et d'effectuer un test statistique.biais de comparaison multiple.

Bias de comparaison multiples'applique à la probabilité accrue de générer incorrectement des valeurs p importantes lors de l'exécution de nombreux tests, car nous devons exécuter un grand nombre de tests. Si nous exécutons 100 tests sur des données aléatoires, nous devrions voir 5 valeurs p inférieures à 0,05. Si vous souhaitez comparer n cibles de trading pour la co-intégration, vous effectuerez n (n-1) / 2 comparaisons, et vous verrez de nombreuses valeurs p incorrectes, qui augmenteront avec l'augmentation de vos échantillons de test. Pour éviter cette situation, sélectionnez quelques paires de trading et vous avez des raisons de déterminer qu'elles peuvent être de co-intégration, puis testez-les séparément.biais de comparaison multiple.

Par conséquent, essayons de trouver quelques cibles de négociation qui montrent la co-intégration. Prenons un panier de grandes actions technologiques américaines dans l'indice S&P 500 comme exemple. Ces cibles de négociation opèrent dans des segments de marché similaires et ont des prix de co-intégration. Nous scannons la liste des objets de négociation et testons la co-intégration entre toutes les paires.

La matrice de score de test de cointégration retournée, la matrice de la valeur de p et toutes les paires dont la valeur de p est inférieure à 0,05.Cette méthode est sujette à des biais de comparaison multiples, de sorte qu'en fait, ils ont besoin de mener une deuxième vérification.Dans cet article, pour faciliter notre explication, nous choisissons d'ignorer ce point de l'exemple.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Remarque: Nous avons inclus le benchmark du marché (SPX) dans les données - le marché a conduit le flux de nombreux objets de négociation. Habituellement, vous pouvez trouver deux objets de négociation qui semblent être cointégrés; Mais en fait, ils ne cointégrent pas les uns avec les autres, mais avec le marché. Ceci est appelé une variable de confusion. Il est important de vérifier la participation du marché dans toute relation que vous trouvez.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Maintenant, essayons d'utiliser notre méthode pour trouver des paires de négociation co-intégrées.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

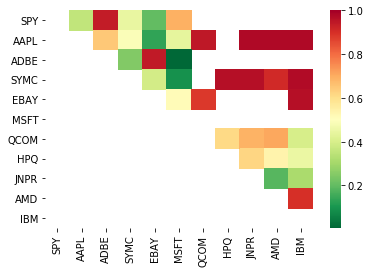
Il semble que ADBE et MSFT soient co-intégrées.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

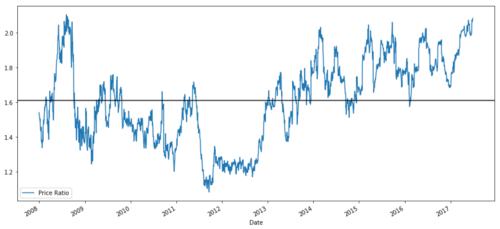
Graphique du rapport de prix entre MSFT et ADBE de 2008 à 2017

Ce ratio ressemble à une moyenne stable. Les ratios absolus ne sont pas statistiquement utiles. Il est plus utile de normaliser nos signaux en les traitant comme un score Z. Le score Z est défini comme:

Le score Z (valeur) = (valeur moyenne) / écart type

Attention!

En fait, nous essayons généralement d'élargir les données en partant du principe que les données sont normalement distribuées. Cependant, de nombreuses données financières ne sont pas normalement distribuées, nous devons donc faire très attention à ne pas simplement supposer la normalité ou une distribution spécifique lors de la génération de statistiques. La vraie distribution des ratios peut avoir un effet de queue de graisse, et ces données qui ont tendance à être extrêmes vont confondre notre modèle et entraîner d'énormes pertes.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

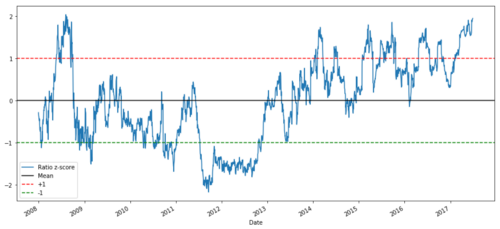
Le ratio de prix Z entre MSFT et ADBE de 2008 à 2017

Maintenant, il est plus facile d'observer le mouvement du ratio près de la valeur moyenne, mais parfois il est facile d'avoir une grande différence par rapport à la valeur moyenne.

Maintenant que nous avons discuté des connaissances de base de la stratégie de trading de paire, et déterminé l'objet de l'intégration conjointe basée sur le prix historique, essayons de développer un signal de trading.

• collecter des données fiables et les nettoyer;

• Créer des fonctions à partir de données pour identifier les signaux/logiques de négociation;

• Les fonctions peuvent être des moyennes mobiles ou des données de prix, des corrélations ou des ratios de signaux plus complexes - les combiner pour créer de nouvelles fonctions;

• Utilisez ces fonctions pour générer des signaux de trading, c'est-à-dire quels signaux sont des achats, des ventes ou des positions courtes à surveiller.

Heureusement, nous avons la plateforme FMZ Quant (fmz.comNous pouvons consacrer notre énergie et notre temps à la conception de la logique stratégique et à l'extension des fonctions.

Dans la plateforme FMZ Quant, il y a des interfaces encapsulées pour différents échanges traditionnels. Ce que nous devons faire est d'appeler ces interfaces API. Le reste de la logique de mise en œuvre sous-jacente a été terminée par une équipe professionnelle.

Afin de compléter la logique et d'expliquer le principe dans cet article, nous présenterons ces logiques sous-jacentes en détail.

On commence:

Étape 1: Posez votre question

Ici, nous essayons de créer un signal pour nous dire si le ratio va acheter ou vendre au moment suivant, c'est-à-dire notre variable de prédiction Y:

Y = Ratio est acheter (1) ou vendre (-1)

Y ((t) = Sign ((Ratio ((t+1) Ratio ((t))

S'il vous plaît noter que nous n'avons pas besoin de prédire le prix cible de la transaction réelle, ou même la valeur réelle du ratio (bien que nous puissions), mais seulement la direction du ratio dans l'étape suivante.

Étape 2: Rassembler des données fiables et précises

FMZ Quant est votre ami! Vous avez juste besoin de spécifier l'objet de transaction à échanger et la source de données à utiliser, et il extraira les données requises et les effacera pour le fractionnement des dividendes et des objets de transaction.

Pour les journées de négociation des 10 dernières années (environ 2500 points de données), nous avons obtenu les données suivantes en utilisant Yahoo Finance: prix d'ouverture, prix de clôture, prix le plus élevé, prix le plus bas et volume des transactions.

Étape 3: diviser les données

N'oubliez pas cette étape très importante pour tester l'exactitude du modèle.

• Formation 7 ans ~ 70%

• Test ~ 3 ans 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

Idéalement, nous devrions également créer des ensembles de validation, mais nous ne le ferons pas pour l'instant.

Étape 4: Ingénierie des caractéristiques

Quelles peuvent être les fonctions connexes? Nous voulons prédire la direction du changement du ratio. Nous avons vu que nos deux cibles de trading sont cointégrées, donc ce ratio a tendance à changer et à revenir à la valeur moyenne. Il semble que nos caractéristiques devraient être des mesures du ratio moyen, et la différence entre la valeur actuelle et la valeur moyenne peut générer notre signal de trading.

Nous utilisons les fonctions suivantes:

• Rapport de la moyenne mobile à 60 jours: mesure de la moyenne mobile;

• Rapport de la moyenne mobile sur 5 jours: mesure de la valeur actuelle de la moyenne;

• déviation type de 60 jours;

• Z Score: (5d MA - 60d MA) / 60d SD.

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

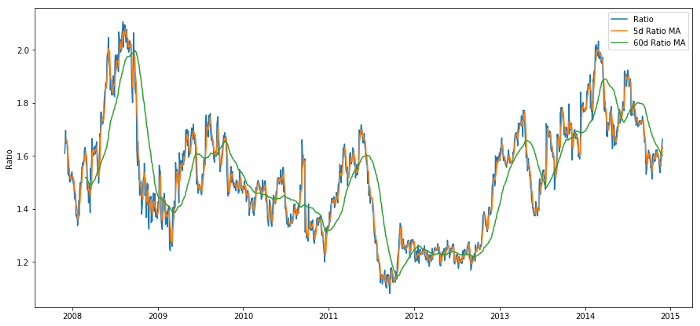
Ratio de prix entre 60d et 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

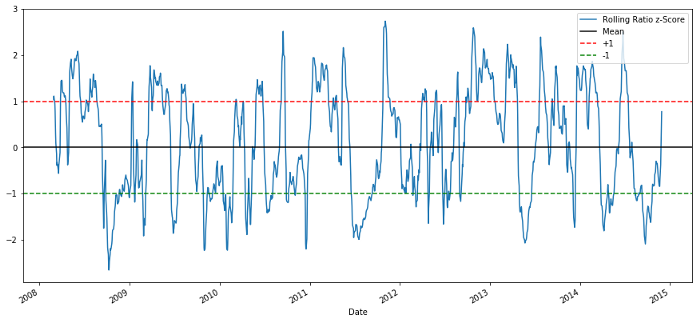
60-5 Z Score coefficients de prix

Le score Z de la valeur moyenne mobile fait ressortir la propriété de régression de la valeur moyenne du ratio!

Étape 5: Sélection du modèle

Commençons par un modèle très simple. En regardant le graphique de score z, nous pouvons voir que si le score z est trop élevé ou trop bas, il reviendra.

• Lorsque z est inférieur à -1.0, le rapport est d'acheter (1), parce que nous nous attendons à z de retourner à 0, donc le rapport augmente;

• Lorsque z est supérieur à 1,0, le rapport est vendu (- 1), parce que nous nous attendons à ce que z revienne à 0, donc le rapport diminue.

Étape 6: Formation, vérification et optimisation

Enfin, jetons un coup d'œil à l'impact réel de notre modèle sur les données réelles.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

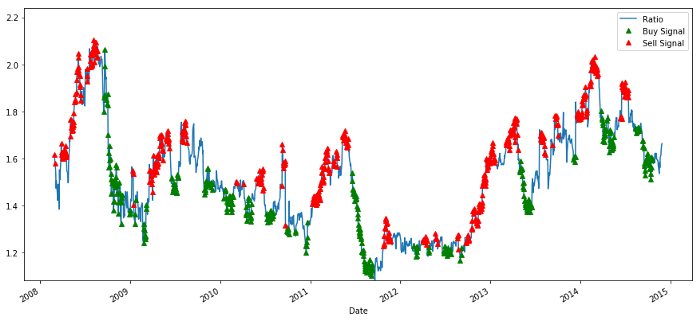
Signal du ratio des prix d'achat et de vente

Le signal semble raisonnable. Nous semblons vendre quand il est élevé ou en augmentation (points rouges) et le racheter quand il est bas (points verts) et en diminution.

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

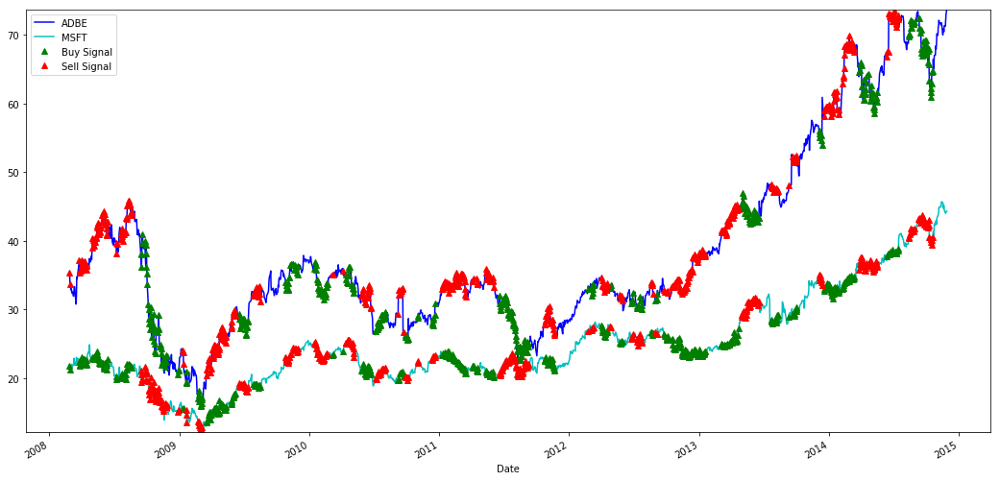
Signaux d'achat et de vente d'actions MSFT et ADBE

S'il vous plaît, faites attention à la façon dont nous faisons parfois des profits sur des jambes courtes, parfois sur des jambes longues, et parfois les deux.

Nous sommes satisfaits du signal des données de formation. Voyons quel type de profit ce signal peut générer. Lorsque le ratio est faible, nous pouvons faire un simple back tester, acheter un ratio (acheter 1 stock ADBE et vendre ratio x stock MSFT), et vendre un ratio (vendre 1 stock ADBE et acheter x ratio MSFT) quand il est élevé, et calculer les transactions PnL de ces ratios.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Le résultat est: 1783.375

Cette stratégie semble donc rentable! Maintenant, nous pouvons optimiser davantage en modifiant la fenêtre de temps moyenne mobile, en modifiant les seuils d'achat/vente et de fermeture des positions, et vérifier l'amélioration de la performance des données de validation.

Nous pouvons également essayer des modèles plus complexes, tels que la régression logistique et SVM, pour prédire 1/-1.

Maintenant, avançons ce modèle, ce qui nous amène à:

Étape 7: vérification des données d'essai

Ici encore, la plateforme FMZ Quant adopte un moteur de backtesting QPS / TPS haute performance pour reproduire l'environnement historique véritablement, éliminer les pièges communs du backtesting quantitatif et découvrir les lacunes des stratégies à temps, afin de mieux aider l'investissement réel du bot.

Pour expliquer le principe, cet article choisit toujours de montrer la logique sous-jacente. Dans l'application pratique, nous recommandons aux lecteurs d'utiliser la plate-forme FMZ Quant. En plus de gagner du temps, il est important d'améliorer le taux de tolérance aux pannes.

Le backtesting est simple. Nous pouvons utiliser la fonction ci-dessus pour afficher le PnL des données de test.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

Le résultat est: 5262 868.

Le modèle a fait un excellent travail, c'est devenu notre premier modèle simple de trading en paires.

Évitez le sur-ajustement

Avant de conclure la discussion, j'aimerais discuter de l'overfitting en particulier. L'overfitting est le piège le plus dangereux dans les stratégies de trading. L'algorithme d'overfitting peut très bien fonctionner dans le backtest mais échouer sur les nouvelles données invisibles - ce qui signifie qu'il ne révèle vraiment aucune tendance des données et n'a pas de réelle capacité de prédiction.

Dans notre modèle, nous utilisons des paramètres de roulement pour estimer et optimiser la longueur de la fenêtre de temps. Nous pouvons décider de simplement itérer sur toutes les possibilités, une durée de fenêtre de temps raisonnable, et choisir la durée de temps en fonction de la meilleure performance de notre modèle.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Maintenant, nous examinons les performances du modèle sur les données d'essai, et nous constatons que cette longueur de fenêtre de temps est loin d'être optimale!

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Il est évident que les données d'échantillonnage qui nous conviennent ne donneront pas toujours de bons résultats à l'avenir.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

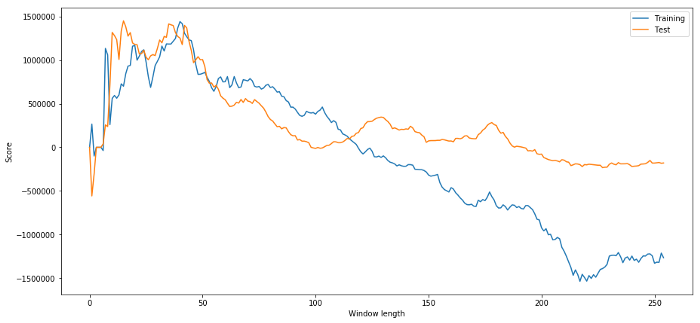
Nous pouvons voir que n'importe quoi entre 20 et 50 est un bon choix pour les fenêtres temporelles.

Pour éviter le surajustement, nous pouvons utiliser le raisonnement économique ou la nature de l'algorithme pour sélectionner la longueur de la fenêtre de temps.

La prochaine étape.

Dans cet article, nous proposons quelques méthodes d'introduction simples pour démontrer le processus d'élaboration de stratégies de trading.

• l'exposant Hurst;

• La demi-vie de la régression moyenne déduite du procédé d'Ornstein-Uhlenbeck;

• Filtreur Kalman.

Relationnée

Plus de